自由度

此词条暂由彩云小译翻译，翻译字数共1459，未经人工整理和审校，带来阅读不便，请见谅。

In physics and chemistry, a degree of freedom is an independent physical parameter in the formal description of the state of a physical system. The set of all states of a system is known as the system's phase space, and the degrees of freedom of the system are the dimensions of the phase space.

In physics and chemistry, a degree of freedom is an independent physical parameter in the formal description of the state of a physical system. The set of all states of a system is known as the system's phase space, and the degrees of freedom of the system are the dimensions of the phase space.

在物理和化学领域中，自由度是对物理系统状态形式描述中的独立物理参数。系统所有状态的集合称为系统的 相空间，系统的自由度是相空间的维数。

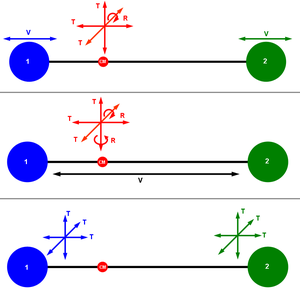
The location of a particle in three-dimensional space requires three position coordinates. Similarly, the direction and speed at which a particle moves can be described in terms of three velocity components, each in reference to the three dimensions of space. If the time evolution of the system is deterministic, where the state at one instant uniquely determines its past and future position and velocity as a function of time, such a system has six degrees of freedom.^{[citation needed]} If the motion of the particle is constrained to a lower number of dimensions – for example, the particle must move along a wire or on a fixed surface – then the system has fewer than six degrees of freedom. On the other hand, a system with an extended object that can rotate or vibrate can have more than six degrees of freedom.

The location of a particle in three-dimensional space requires three position coordinates. Similarly, the direction and speed at which a particle moves can be described in terms of three velocity components, each in reference to the three dimensions of space. If the time evolution of the system is deterministic, where the state at one instant uniquely determines its past and future position and velocity as a function of time, such a system has six degrees of freedom. If the motion of the particle is constrained to a lower number of dimensions – for example, the particle must move along a wire or on a fixed surface – then the system has fewer than six degrees of freedom. On the other hand, a system with an extended object that can rotate or vibrate can have more than six degrees of freedom.

一个粒子在三维空间中的位置需要三个位置坐标进行标识。类似地，我们也可以根据三个速度分量来描述粒子运动的方向和速度，每个速度分量都参考该空间的三个维度。如果系统的时间演变是确定的，那么其中某个瞬间以及其过去和未来瞬间的位置和速度，均可以被该瞬间的状态确定为时间函数，相应地，这种系统具有六个自由度。如果将粒子的运动轨迹限制在更小的维度里面，例如，粒子必须沿着电线或在固定的表面上移动，那么系统的自由度则小于6。另一方面，如果一个系统带有可旋转或振动的扩展对象，那么它的自由度将大于6。

In classical mechanics, the state of a point particle at any given time is often described with position and velocity coordinates in the Lagrangian formalism, or with position and momentum coordinates in the Hamiltonian formalism.

在经典力学中，任何给定时间下质点的状态，不同的力学形式会有不一样的描述，在拉格朗日力学中描述为位置和速度坐标，而在哈密顿力学中则描述为位置和动量坐标。

In statistical mechanics, a degree of freedom is a single scalar number describing the microstate of a system.^[1] The specification of all microstates of a system is a point in the system's phase space.

In statistical mechanics, a degree of freedom is a single scalar number describing the microstate of a system. The specification of all microstates of a system is a point in the system's phase space.

在统计力学中，自由度是描述系统微观状态的单个标量数。一个系统所有微观状态的规格参数都是基于该系统相空间中的一个点。

In the 3D ideal chain model in chemistry, two angles are necessary to describe the orientation of each monomer.

在化学的三维 理想链模型中，描述每个单元结构方向的必要参数是它们的两个角度。

It is often useful to specify quadratic degrees of freedom. These are degrees of freedom that contribute in a quadratic function to the energy of the system.

指定二次自由度通常很重要。因为它们有助于建立系统能量的二次函数。

Gas molecules 气体分子

可视化双原子分子六个自由度的不同方式。（其中CM：系统的质心，T：平移运动，R：旋转运动，V：振动运动。）

In three-dimensional space, three degrees of freedom are associated with the movement of a particle. A diatomic gas molecule has 6 degrees of freedom模板:Dubious. This set may be decomposed in terms of translations, rotations, and vibrations of the molecule. The center of mass motion of the entire molecule accounts for 3 degrees of freedom. In addition, the molecule has two rotational degrees of motion and one模板:Dubious vibrational mode. The rotations occur around the two axes perpendicular to the line between the two atoms. The rotation around the atom–atom bond is not a physical rotation模板:Dubious. This yields, for a diatomic molecule, a decomposition of:

In three-dimensional space, three degrees of freedom are associated with the movement of a particle. A diatomic gas molecule has 6 degrees of freedom. This set may be decomposed in terms of translations, rotations, and vibrations of the molecule. The center of mass motion of the entire molecule accounts for 3 degrees of freedom. In addition, the molecule has two rotational degrees of motion and one vibrational mode. The rotations occur around the two axes perpendicular to the line between the two atoms. The rotation around the atom–atom bond is not a physical rotation. This yields, for a diatomic molecule, a decomposition of:

在三维空间中，粒子的运动与它的三个自由度有关。双原子气体分子具有6个自由度（存在争议）。因此可以根据其分子的平移，旋转和振动来分解该运动集合。整个分子的质心运动具有3个自由度，除此之外，还具有两个旋转自由度和一个[存在争议]振动自由度。其中旋转运动是围绕垂直于两个原子之间的连线轴发生的。值得注意的是这里围绕原子和原子键的旋转并不是物理旋转[存在争议]。因此对于双原子分子，可以将其分解为：

[math]\displaystyle{ N = 6 = 3 + 2 + 1. }[/math]

For a general, non-linear molecule, all 3 rotational degrees of freedom are considered, resulting in the decomposition:

对于一般的非线性分子，其所有的3个旋转自由度均需考虑，因此它的分解形式为：

[math]\displaystyle{ 3N = 3 + 3 + (3N - 6) }[/math]

which means that an $N$ -atom molecule has $3 N - 6$ vibrational degrees of freedom for $N > 2$ . In special cases, such as adsorbed large molecules, the rotational degrees of freedom can be limited to only one.^[2]

which means that an -atom molecule has vibrational degrees of freedom for . In special cases, such as adsorbed large molecules, the rotational degrees of freedom can be limited to only one.

这意味着当N>2时，N原子分子具有3N-6个振动自由度。不过在特殊情况下，例如一个吸附的大分子，旋转自由度只能限制为一个。

As defined above one can also count degrees of freedom using the minimum number of coordinates required to specify a position. This is done as follows:

如上所述，还可以使用指定维度空间所需的最少坐标数来确定自由度。比如：

For a single particle we need 2 coordinates in a 2-D plane to specify its position and 3 coordinates in 3-D space. Thus its degree of freedom in a 3-D space is 3.

For a single particle we need 2 coordinates in a 2-D plane to specify its position and 3 coordinates in 3-D space. Thus its degree of freedom in a 3-D space is 3.

对于单个粒子，我们需要在二维平面中指定2个坐标，在三维空间中指定3个坐标。因此，它在三维空间中的自由度为3。

For a body consisting of 2 particles (ex. a diatomic molecule) in a 3-D space with constant distance between them (let's say d) we can show (below) its degrees of freedom to be 5.

For a body consisting of 2 particles (ex. a diatomic molecule) in a 3-D space with constant distance between them (let's say d) we can show (below) its degrees of freedom to be 5.

在三维空间中，由2个粒子（例如双原子分子）组成且彼此之间具有恒定距离（假设d）的物体，我们可以（在下面）显示其自由度为5。

Let's say one particle in this body has coordinate $(x 1, y 1, z 1)$ and the other has coordinate $(x 2, y 2, z 2)$ with $z 2$ unknown. Application of the formula for distance between two coordinates

Let's say one particle in this body has coordinate and the other has coordinate with unknown. Application of the formula for distance between two coordinates

假设这个物体中的一个粒子的坐标为 $(x 1, y 1, z 1)$ ，另一个粒子的坐标为 $(x 2, y 2, z 2)$ ，其中 $z 2$ 未知。那么两个坐标之间距离的公式可以描述为：

[math]\displaystyle{ d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2} }[/math]

results in one equation with one unknown, in which we can solve for $z 2$ . One of $x 1$ , $x 2$ , $y 1$ , $y 2$ , $z 1$ , or $z 2$ can be unknown.

results in one equation with one unknown, in which we can solve for . One of , , , , , or can be unknown.

其等式含有一个未知数 $z 2$ ，不过我们可以对其求解。因此实际上是允许 $x 1$ , $x 2$ , $y 1$ , $y 2$ , $z 1$ , 或者 $z 2$ 其中之一是未知的。

Contrary to the classical equipartition theorem, at room temperature, the vibrational motion of molecules typically makes negligible contributions to the heat capacity. This is because these degrees of freedom are frozen because the spacing between the energy eigenvalues exceeds the energy corresponding to ambient temperatures ( $k B T$ ). In the following table such degrees of freedom are disregarded because of their low effect on total energy. Then only the translational and rotational degrees of freedom contribute, in equal amounts, to the heat capacity ratio. This is why $γ$ = $模板:Sfrac$ for monatomic gases and $γ$ = $模板:Sfrac$ for diatomic gases at room temperature.

Contrary to the classical equipartition theorem, at room temperature, the vibrational motion of molecules typically makes negligible contributions to the heat capacity. This is because these degrees of freedom are frozen because the spacing between the energy eigenvalues exceeds the energy corresponding to ambient temperatures (). In the following table such degrees of freedom are disregarded because of their low effect on total energy. Then only the translational and rotational degrees of freedom contribute, in equal amounts, to the heat capacity ratio. This is why =}} for monatomic gases and =}} for diatomic gases at room temperature.

与经典的能量均分定理相反，在室温下，分子的振动运动对热容的贡献可以忽略不计。这是因为这些自由度是冻结的，因为能量本征值之间的间距超过了对应于环境温度的能量()。在下表中，这种自由度不予考虑，因为它们对总能量的影响很小。那么，只有平动自由度和转动自由度，以相等的数量贡献于热容比。这就是为什么对于单原子气体和对于室温下的双原子气体。

However, at very high temperatures, on the order of the vibrational temperature (Θ_vib), vibrational motion cannot be neglected.

然而，在非常高的温度下，按振动温度(θ < sub > vib )的顺序，振动运动是不可忽略的。

Vibrational temperatures are between 10³ K and 10⁴ K.^[1]

Vibrational temperatures are between 10³ K and 10⁴ K.

振动温度在10 < sup > 3 k 和10 < sup > 4 k 之间。

{ | class = “ wikitable”

			Monatomic	Monatomic	单原子的	Linear molecules	Linear molecules	线性分子	Non-linear molecules	Non-linear molecules	非线性分子
Translation ( $x$ , $y$ , and $z$ )	Translation (, , and )	翻译(，，和)	3	3	3	3	3	3	3	3	3
Rotation ( $x$ , $y$ , and $z$ )	Rotation (, , and )	旋转(、和)	0	0	0	2	2	2	3	3	3
Total (disregarding Vibration at room temperatures)	Total (disregarding Vibration at room temperatures)	总计(不包括室温下的振动)	3	3	3	5	5	5	6	6	6
Vibration	Vibration	震动	0	0	0	$3 N - 5$			$3 N - 6$
Total (including Vibration)	Total (including Vibration)	总数(包括振动)	3	3	3	3N	3N	3N	3N	3N	3N

|}

Independent degrees of freedom

The set of degrees of freedom $X 1, ... , X N$ of a system is independent if the energy associated with the set can be written in the following form:

The set of degrees of freedom of a system is independent if the energy associated with the set can be written in the following form:

系统的自由度集合是独立的，如果与该自由度集合相关的能量可以写成下列形式:

[math]\displaystyle{ E = \sum_{i=1}^N E_i(X_i), }[/math]

[数学] ，[数学]

where $E i$ is a function of the sole variable $X i$ .

where is a function of the sole variable .

这里是唯一变量的函数。

example: if $X 1$ and $X 2$ are two degrees of freedom, and $E$ is the associated energy:

example: if and are two degrees of freedom, and is the associated energy:

例如: 如果和是两个自由度，关联的能量是:

If [math]\displaystyle{ E = X_1^4 + X_2^4 }[/math], then the two degrees of freedom are independent.

If [math]\displaystyle{ E = X_1^4 + X_2^4 }[/math], then the two degrees of freedom are independent.

如果 < math > e = x _ 1 ^ 4 + x _ 2 ^ 4 </math > ，那么这两个自由度是独立的。

If [math]\displaystyle{ E = X_1^4 + X_1 X_2 + X_2^4 }[/math], then the two degrees of freedom are not independent. The term involving the product of $X 1$ and $X 2$ is a coupling term that describes an interaction between the two degrees of freedom.

If [math]\displaystyle{ E = X_1^4 + X_1 X_2 + X_2^4 }[/math], then the two degrees of freedom are not independent. The term involving the product of and is a coupling term that describes an interaction between the two degrees of freedom.

如果 < math > e = x 1 ^ 4 + x 1 x 2 + x 2 ^ 4 </math > ，那么这两个自由度不是独立的。包含和乘积的术语是描述两个自由度之间相互作用的耦合术语。

For $i$ from 1 to $N$ , the value of the $i$ th degree of freedom $X i$ is distributed according to the Boltzmann distribution. Its probability density function is the following:

For from 1 to , the value of the th degree of freedom is distributed according to the Boltzmann distribution. Its probability density function is the following:

对于从1到1，第四自由度的值是按照美国波兹曼分布协会的标准分配的。它的概率密度函数如下:

[math]\displaystyle{ p_i(X_i) = \frac{e^{-\frac{E_i}{k_B T}}}{\int dX_i \, e^{-\frac{E_i}{k_B T}}} }[/math],

[math]\displaystyle{ p_i(X_i) = \frac{e^{-\frac{E_i}{k_B T}}}{\int dX_i \, e^{-\frac{E_i}{k_B T}}} }[/math],

[数学][数学]

In this section, and throughout the article the brackets [math]\displaystyle{ \langle \rangle }[/math] denote the mean of the quantity they enclose.

在本节中，整篇文章中括号 < math > langle rangle </math > 表示它们所包含的量的平均值。

The internal energy of the system is the sum of the average energies associated with each of the degrees of freedom:

系统的内能是与每个自由度有关的平均能量之和:

[math]\displaystyle{ \langle E \rangle = \sum_{i=1}^N \langle E_i \rangle. }[/math]

数学，数学，数学

Quadratic degrees of freedom

A degree of freedom $X i$ is quadratic if the energy terms associated with this degree of freedom can be written as

A degree of freedom is quadratic if the energy terms associated with this degree of freedom can be written as

如果与这个自由度相关的能量项可以写成二次方程，则该自由度为二次方程

[math]\displaystyle{ E = \alpha_i\,\,X_i^2 + \beta_i \,\, X_i Y }[/math],

数学 e = alpha _ i，，x _ i ^ 2 + beta _ i，，x _ i y,

where $Y$ is a linear combination of other quadratic degrees of freedom.

where is a linear combination of other quadratic degrees of freedom.

其他二次自由度的线性组合。

example: if $X 1$ and $X 2$ are two degrees of freedom, and $E$ is the associated energy:

example: if and are two degrees of freedom, and is the associated energy:

例如: 如果和是两个自由度，关联的能量是:

If [math]\displaystyle{ E = X_1^4 + X_1^3 X_2 + X_2^4 }[/math], then the two degrees of freedom are not independent and non-quadratic.

If [math]\displaystyle{ E = X_1^4 + X_1^3 X_2 + X_2^4 }[/math], then the two degrees of freedom are not independent and non-quadratic.

如果 < math > e = x _ 1 ^ 4 + x _ 1 ^ 3 x _ 2 + x _ 2 ^ 4 </math > ，那么这两个自由度不是独立的和非二次的。

If [math]\displaystyle{ E = X_1^4 + X_2^4 }[/math], then the two degrees of freedom are independent and non-quadratic.

If [math]\displaystyle{ E = X_1^4 + X_2^4 }[/math], then the two degrees of freedom are independent and non-quadratic.

如果 < math > e = x _ 1 ^ 4 + x _ 2 ^ 4 </math > ，那么这两个自由度是独立的和非二次的。

If [math]\displaystyle{ E = X_1^2 + X_1 X_2 + 2X_2^2 }[/math], then the two degrees of freedom are not independent but are quadratic.

If [math]\displaystyle{ E = X_1^2 + X_1 X_2 + 2X_2^2 }[/math], then the two degrees of freedom are not independent but are quadratic.

如果 < math > e = x 1 ^ 2 + x 1 x 2 + 2 x 2 ^ 2 </math > ，那么这两个自由度不是独立的，而是二次的。

If [math]\displaystyle{ E = X_1^2 + 2X_2^2 }[/math], then the two degrees of freedom are independent and quadratic.

If [math]\displaystyle{ E = X_1^2 + 2X_2^2 }[/math], then the two degrees of freedom are independent and quadratic.

如果 < math > e = x _ 1 ^ 2 + 2 x _ 2 ^ 2 </math > ，那么这两个自由度是独立的和二次的。

For example, in Newtonian mechanics, the dynamics of a system of quadratic degrees of freedom are controlled by a set of homogeneous linear differential equations with constant coefficients.

例如，在牛顿运动定律，二次自由度系统的动力学是由一组常系数齐次线性微分方程组控制的。

Quadratic and independent degree of freedom

$X 1, ... , X N$ are quadratic and independent degrees of freedom if the energy associated with a microstate of the system they represent can be written as:

are quadratic and independent degrees of freedom if the energy associated with a microstate of the system they represent can be written as:

是二次自由度和独立自由度，如果与它们所代表的系统的微观状态相关的能量可以写成:

[math]\displaystyle{ E = \sum_{i=1}^N \alpha_i X_i^2 }[/math]

< math > e = sum { i = 1} ^ n alpha _ i x _ i ^ 2

Equipartition theorem

In the classical limit of statistical mechanics, at thermodynamic equilibrium, the internal energy of a system of $N$ quadratic and independent degrees of freedom is:

In the classical limit of statistical mechanics, at thermodynamic equilibrium, the internal energy of a system of quadratic and independent degrees of freedom is:

在统计力学的经典极限下，在热力学平衡，一个二次独立自由度系统的内能是:

[math]\displaystyle{ U = \langle E \rangle = N\,\frac{k_B T}{2} }[/math]

[math]\displaystyle{ U = \langle E \rangle = N\,\frac{k_B T}{2} }[/math]

[数学] u = langle e rangle = n，frac { k _ b t }{2}[数学]

Here, the mean energy associated with a degree of freedom is:

在这里，与一定自由度相关的平均能是:

[math]\displaystyle{ \langle E_i \rangle = \int dX_i\,\,\alpha_i X_i^2\,\, p_i(X_i) = \frac{\int dX_i\,\,\alpha_i X_i^2\,\, e^{-\frac{\alpha_i X_i^2}{k_B T}}}{\int dX_i\,\, e^{-\frac{\alpha_i X_i^2}{k_B T}}} }[/math]

2，，p _ i (xi) = frac { int dX _ i，，alpha _ i x _ i ^ 2，，e ^ {-frac { alpha _ i x _ i ^ 2，，e ^ {-frac { i x _ i ^ 2}}{ k _ b t }}{ int dX _ i，e ^ {-frac { alpha _ i x _ i ^ 2}}{ k _ b _ i，e ^ {-frac { i x _ i ^ 2}{ k _ b _ t }} </math >

[math]\displaystyle{ \langle E_i \rangle = \frac{k_B T}{2}\frac{\int dx\,\,x^2\,\, e^{-\frac{x^2}{2}}}{\int dx\,\, e^{-\frac{x^2}{2}}} = \frac{k_B T}{2} }[/math]

{2} frac { int dx，，x ^ 2，，e ^ {-frac { x ^ 2}{2}}}{ int dx，，e ^ {-frac { x ^ 2}{2}}}{ e ^ {-frac { x ^ 2}{2}}}}} = frac { k _ b }{2} </math >

Since the degrees of freedom are independent, the internal energy of the system is equal to the sum of the mean energy associated with each degree of freedom, which demonstrates the result.

由于自由度是独立的，系统的内能等于与每个自由度相关的平均能量之和，从而证明了这一结果。

Generalizations

The description of a system's state as a point in its phase space, although mathematically convenient, is thought to be fundamentally inaccurate. In quantum mechanics, the motion degrees of freedom are superseded with the concept of wave function, and operators which correspond to other degrees of freedom have discrete spectra. For example, intrinsic angular momentum operator (which corresponds to the rotational freedom) for an electron or photon has only two eigenvalues. This discreteness becomes apparent when action has an order of magnitude of the Planck constant, and individual degrees of freedom can be distinguished.

将一个系统的状态描述为其相空间中的一个点，虽然在数学上很方便，但被认为是根本不准确的。在量子力学中，运动自由度被波函数的概念所取代，相应于其他自由度的运算符具有离散谱。例如，一个电子或光子的内禀角动量算符(相当于转动自由度)只有两个本征值。当作用力的数量级为普朗克常数时，这种离散性变得显而易见，个体自由度也可以区分。

References

↑ ^1.0 ^1.1 Reif, F. (2009). Fundamentals of Statistical and Thermal Physics. Long Grove, IL: Waveland Press, Inc.. p. 51. ISBN 1-57766-612-7.
↑ Waldmann, Thomas; Klein, Jens; Hoster, Harry E.; Behm, R. Jürgen (2013). "Stabilization of Large Adsorbates by Rotational Entropy: A Time-Resolved Variable-Temperature STM Study". ChemPhysChem. 14 (1): 162–9. doi:10.1002/cphc.201200531. PMID 23047526.

Category:Concepts in physics

分类: 物理概念

Category:Dimension

类别: 维度

This page was moved from wikipedia:en:Degrees of freedom (physics and chemistry). Its edit history can be viewed at 自由度/edithistory

[:0-1] 1.0 ^1.1 Reif, F. (2009). Fundamentals of Statistical and Thermal Physics. Long Grove, IL: Waveland Press, Inc.. p. 51. ISBN 1-57766-612-7.

[2] Waldmann, Thomas; Klein, Jens; Hoster, Harry E.; Behm, R. Jürgen (2013). "Stabilization of Large Adsorbates by Rotational Entropy: A Time-Resolved Variable-Temperature STM Study". ChemPhysChem. 14 (1): 162–9. doi:10.1002/cphc.201200531. PMID 23047526.

[1]

[2]

自由度

目录