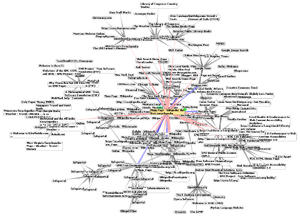
图的绘制 Graph drawing

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
跳到导航 跳到搜索

本词条由Ryan初步翻译 由CecileLi初步审校 于2020.11.19再次审校，若有遗漏敬请谅解。

25px  此article介紹的是the general subject of graph drawing。For the annual research symposium, see International Symposium on Graph Drawing.
图1：Graphic representation of a minute fraction of the WWW, demonstrating hyperlinks. 以图的形式展示万维网的一小部分


Graph drawing is an area of mathematics and computer science combining methods from geometric graph theory and information visualization to derive two-dimensional depictions of graphs arising from applications such as social network analysis, cartography, linguistics, and bioinformatics.[1]


图的绘制 Graph Drawing是数学和计算机科学的一个交叉领域，它结合了[[几何图形理论 geometric graph theory]]和 信息可视化 information visualization的方法，可以用于对来自社会网络分析、制图学、语言学和生物信息学等各种应用场景进行二维描述。


图形或网络图 network diagram的绘制是通过从图形抽象出的顶点和边表示的。这里说的图不应与图形本身混淆：毫不相似的图可以对应于同一个图形。[2]抽象地说，重要的是哪一对顶点是由边连在一起。然而，在具体的绘图中，这些顶点和边的排列影响了它的可理解性、可用性、制造成本和美学。[3]如果图形通过添加和删除边缘（动态绘制图形）而随时间变化，并且目的是保存用户的心理映射，那么问题会变得更糟糕。[4]


绘图惯例 Graphical conventions

图2：带箭头显示边方向的有向图

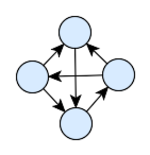
图经常绘制成节点链接图，其中顶点可以是为圆框、方框或文本标签，边表示为欧式平面 Euclidean Plane上的线段、折线或曲线。[3]节点链接图可以追溯到13世纪雷蒙·卢尔 Ramon Llull的作品，他为得到完全图，绘制了这种类型的图，以便分析形而上学概念集合之间的所有成对组合。[5]


在有向图中，绘图惯例规定用箭头表示它们的方向；[2] 然而，用户研究表明，其他惯例（例如，渐缩）可以更有效地提供此信息。[6]向上的平面绘图绘图惯例是，每个边都从较低的顶点定向到较高的顶点，因此就不再需要箭头。[7]


Alternative conventions to node–link diagrams include adjacency representations such as circle packings, in which vertices are represented by disjoint regions in the plane and edges are represented by adjacencies between regions; intersection representations in which vertices are represented by non-disjoint geometric objects and edges are represented by their intersections; visibility representations in which vertices are represented by regions in the plane and edges are represented by regions that have an unobstructed line of sight to each other; confluent drawings, in which edges are represented as smooth curves within mathematical train tracks; fabrics, in which nodes are represented as horizontal lines and edges as vertical lines;[8] and visualizations of the adjacency matrix of the graph.

Alternative conventions to node–link diagrams include adjacency representations such as circle packings, in which vertices are represented by disjoint regions in the plane and edges are represented by adjacencies between regions; intersection representations in which vertices are represented by non-disjoint geometric objects and edges are represented by their intersections; visibility representations in which vertices are represented by regions in the plane and edges are represented by regions that have an unobstructed line of sight to each other; confluent drawings, in which edges are represented as smooth curves within mathematical train tracks; fabrics, in which nodes are represented as horizontal lines and edges as vertical lines; and visualizations of the adjacency matrix of the graph.

节点链接图的替代约定包括邻接表示，例如圆堆积，其中，顶点由平面中的不相交区域表示，边缘由区域之间的邻接表示； 交点表示，其中顶点由不相交的几何对象表示，而边线由其交点表示； 可见性表示，其中顶点由平面中的区域表示，边缘由彼此无障碍视线的区域表示； 融合图，其中边缘表示为数学火车轨道内的平滑曲线； 织物，其中节点表示为水平线，边缘表示为垂直线； 以及图表的邻接矩阵的可视化。

节点链接图的替代绘制替代，包括邻接表示法，如圆填充 Circle Packings，其中，顶点表示为平面上不相交的区域，边表示为区域之间的邻接； 交点表示 Intersection representations，其中顶点由非相交的几何对象表示，而边由其交点表示；可见性：其中顶点由平面中的区域表示，边由彼此无视线障碍的区域表示; 汇流图，其中边表示为数学轨迹上的光滑曲线; 连接物，其中顶点表示为水平线，边表示为垂直线; 以及图形邻接矩阵 Adjiacency Matrix的可视化结点。

质量度量 Quality measures

Many different quality measures have been defined for graph drawings, in an attempt to find objective means of evaluating their aesthetics and usability.[9] In addition to guiding the choice between different layout methods for the same graph, some layout methods attempt to directly optimize these measures.

Many different quality measures have been defined for graph drawings, in an attempt to find objective means of evaluating their aesthetics and usability. In addition to guiding the choice between different layout methods for the same graph, some layout methods attempt to directly optimize these measures.

为了找到客观评价图形美观性和可用性的方法，我们定义了许多不同的图形质量度量方法。除了用于指导对同一图形的不同布局方法之间的选择之外，某些布局方法还尝试直接优化度量方式。

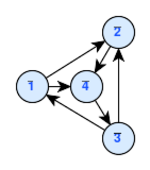
图3：Planar graph drawn without overlapping edges 没有重叠边的平面图



  • The crossing number of a drawing is the number of pairs of edges that cross each other. If the graph is planar, then it is often convenient to draw it without any edge intersections; that is, in this case, a graph drawing represents a graph embedding. However, nonplanar graphs frequently arise in applications, so graph drawing algorithms must generally allow for edge crossings.[10]

图的交叉数 Crossing Number是相交的成对的边的数目。如果图形是平面的，那么我们通常可以方便地画出没有任何边缘相交的图形;也就是说，在本例中，图形绘制表示图形嵌入 Graph Embedding。然而，实际应用中经常出现非平面图，因此图形绘制算法通常必须考虑边缘交叉。

  • The area of a drawing is the size of its smallest bounding box, relative to the closest distance between any two vertices. Drawings with smaller area are generally preferable to those with larger area, because they allow the features of the drawing to be shown at greater size and therefore more legibly. The aspect ratio of the bounding box may also be important.

一个图形的面积是它的最小边界盒 Bounding Box的大小，与任意两个顶点之间的最近距离有关。面积小的图通常比面积大的图更可取，因为它们可以让图画的特征以更大的尺寸显示，从而更醒目。当然，边框的纵横比也很重要。

  • Symmetry display is the problem of finding symmetry groups within a given graph, and finding a drawing that displays as much of the symmetry as possible. Some layout methods automatically lead to symmetric drawings; alternatively, some drawing methods start by finding symmetries in the input graph and using them to construct a drawing.[11]

对称显示的问题是在给定的图形中找到对称组 Symmetry Groups，并找到尽可能多地显示对称的绘图。一些布局方法自动形成对称图形;另外，一些绘图方法从查找输入图形中的对称性开始，并使用它们来构造绘图。

  • It is important that edges have shapes that are as simple as possible, to make it easier for the eye to follow them. In polyline drawings, the complexity of an edge may be measured by its number of bends, and many methods aim to provide drawings with few total bends or few bends per edge. Similarly for spline curves the complexity of an edge may be measured by the number of control points on the edge.

重要的是，边缘的形状要尽可能简单，以便更容易循着它们的轨迹观察。在折线图中，一条边的复杂性可以通过它的弯曲数来衡量，多数方法的目的是提供很少的总弯曲或每条边很少弯曲的图。类似地，对于样条曲线，边的复杂性可以通过边上控制点的数量来度量。

  • Several commonly used quality measures concern lengths of edges: it is generally desirable to minimize the total length of the edges as well as the maximum length of any edge. Additionally, it may be preferable for the lengths of edges to be uniform rather than highly varied.

几种常用的质量度量方法与边的长度有关:通常需要最小化边的总长度以及任何边的最大长度。此外，最好使边缘的长度一致而不是差别很大。

  • Angular resolution is a measure of the sharpest angles in a graph drawing. If a graph has vertices with high degree then it necessarily will have small angular resolution, but the angular resolution can be bounded below by a function of the degree.[12]

角度分辨率 Angular Resolution是图形绘制中最小的锐角的度数。如果一个图的顶点高度高，那么它的角分辨率就很小，但是角分辨率也可以由角的函数来限定。

  • The slope number of a graph is the minimum number of distinct edge slopes needed in a drawing with straight line segment edges (allowing crossings). Cubic graphs have slope number at most four, but graphs of degree five may have unbounded slope number; it remains open whether the slope number of degree-4 graphs is bounded.[12]

图的斜率 Slope Number是在具有直线段边(允许交叉)的图中所需的明显边缘斜率的最小值。三次图 Cubic Graphs的斜率最大为4，五次图的斜率数可能是无界的，但四次的图的斜率是否有界仍然有待求证的。

Layout methods 布局方法

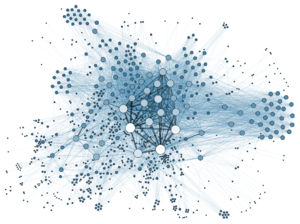
图4：A force-based network visualization. 基于力的网络可视化 [13]

There are many different graph layout strategies:

There are many different graph layout strategies:

有许多不同的图形布局方法:

  • In force-based layout systems, the graph drawing software modifies an initial vertex placement by continuously moving the vertices according to a system of forces based on physical metaphors related to systems of springs or molecular mechanics. Typically, these systems combine attractive forces between adjacent vertices with repulsive forces between all pairs of vertices, in order to seek a layout in which edge lengths are small while vertices are well-separated. These systems may perform gradient descent based minimization of an energy function, or they may translate the forces directly into velocities or accelerations for the moving vertices.[14]

在''基于力的布局系统 Force-Based Layout中，图形绘制软件根据基于弹簧系统或分子力学的物理隐含的力系统，不断移动顶点来修改初始顶点的位置。通常，这些系统将相邻顶点之间的吸引力与所有对顶点之间的排斥力结合起来，以寻求一种边长较小而顶点分离良好的布局。这些系统可以执行梯度下降 Gradient Descent最小化的能量函数，或可以把力直接转化为节点的速度或加速度

频谱布局方法 Spectral Layout，以从图的邻接矩阵派生的矩阵（例如Laplacian）的特征向量 Eigenvector作为坐标。

  • Orthogonal layout methods, which allow the edges of the graph to run horizontally or vertically, parallel to the coordinate axes of the layout. These methods were originally designed for VLSI and PCB layout problems but they have also been adapted for graph drawing. They typically involve a multiphase approach in which an input graph is planarized by replacing crossing points by vertices, a topological embedding of the planarized graph is found, edge orientations are chosen to minimize bends, vertices are placed consistently with these orientations, and finally a layout compaction stage reduces the area of the drawing.[16]

正交布局方法，允许图形的边缘水平或垂直运行，平行于布局的坐标轴。这些方法最初是为超大规模集成电路和PCB布局问题而设计的，但它们也适用于图形绘制。它们通常涉及到一种多阶段的方法，通过用顶点替换交叉点来平面化输入图，找到一个平面化图的拓扑嵌入，选择边的方向来最小化弯曲，顶点的放置始终与这些方向一致，最后一个布局压缩阶段减少图形面积。

  • Tree layout algorithms these show a rooted tree-like formation, suitable for trees. Often, in a technique called "balloon layout", the children of each node in the tree are drawn on a circle surrounding the node, with the radii of these circles diminishing at lower levels in the tree so that these circles do not overlap.[17]

这些树形布局算法显示了一种类似树的根状结构，适合树状图。通常，在一种称为气球布局的技术中，树状图每个节点的子节点被画在围绕该节点的圆上，这些圆的半径在树的较低层次上递减，因此这些圆不会重叠。

  • Layered graph drawing methods (often called Sugiyama-style drawing) are best suited for directed acyclic graphs or graphs that are nearly acyclic, such as the graphs of dependencies between modules or functions in a software system. In these methods, the nodes of the graph are arranged into horizontal layers using methods such as the Coffman–Graham algorithm, in such a way that most edges go downwards from one layer to the next; after this step, the nodes within each layer are arranged in order to minimize crossings.[18]

分层图绘制方法 Layered Graph Drawing(通常称为杉山式图)最适合于有向无环图 Directed Acyclic Graphs或接近无环的图，例如软件系统中模块或函数之间的依赖关系图。在这些方法中，图的节点使用Coffman Graham算法等方法被安排到水平层中，以这样的方式，大多数边从一层向下到下一层;在这一步之后，以最小化交叉将每一层内的节点进行排列。

图5：Arc diagram 弧线图


  • Arc diagrams, a layout style dating back to the 1960s,[19] place vertices on a line; edges may be drawn as semicircles above or below the line, or as smooth curves linked together from multiple semicircles.

弧图 Arc Diagram，一种布局风格可以追溯到20世纪60年代，将顶点放在一条直线上;边缘可以画成在直线上方或下方的半圆，也可以画成由多个半圆连接在一起的光滑曲线。

  • Circular layout methods place the vertices of the graph on a circle, choosing carefully the ordering of the vertices around the circle to reduce crossings and place adjacent vertices close to each other. Edges may be drawn either as chords of the circle or as arcs inside or outside of the circle. In some cases, multiple circles may be used.[20]

圆形布局方法 Circular Layout将图形的顶点放置在一个圆上，仔细选择圆周上顶点的顺序，以减少交叉，并将相邻的顶点放置在彼此接近的位置。边可以画成圆的弦，也可以画成圆内外的弧线。在某些情况下，可以使用多个圆。

  • Dominance drawing places vertices in such a way that one vertex is upwards, rightwards, or both of another if and only if it is reachable from the other vertex. In this way, the layout style makes the reachability relation of the graph visually apparent.[21]

优势图 Dominance Drawing当且仅当一个顶点可以从另一个顶点到达时，画顶点的最优方式是:一个顶点向上，或向右，或两个顶点同时向上。这样，布局风格使得图的可达性关系在视觉上变得明显。

Application-specific graph drawings 专用图

Graphs and graph drawings arising in other areas of application include

Graphs and graph drawings arising in other areas of application include

在其他应用领域出现的图和图绘制包括

社会图 Sociogram，社会网络图，通常由社会网络分析软件提供

哈塞图 Hasse Diagram，一种专门用于部分顺序的图形绘制

''Dessin d'enfants，代数几何中使用的一种图形画法

状态图 State Diagram，有限状态机的图形表示

计算机网络图 Computer Network Diagram，描述计算机网络中的节点和连接

流程图 Flowchart和drakon图，其中节点表示算法的步骤，边表示步骤之间的控制流的绘图。

  • Data-flow diagrams, drawings in which the nodes represent the components of an information system and the edges represent the movement of information from one component to another.

数据流程图 Data-Flow Diagram，其中节点表示信息系统的组件，边缘表示信息从一个组件到另一个组件的移动。

生物信息学包括系统发育树，蛋白质，蛋白质相互作用网络，和代谢途径。


In addition, the placement and routing steps of electronic design automation (EDA) are similar in many ways to graph drawing, as is the problem of greedy embedding in distributed computing, and the graph drawing literature includes several results borrowed from the EDA literature. However, these problems also differ in several important ways: for instance, in EDA, area minimization and signal length are more important than aesthetics, and the routing problem in EDA may have more than two terminals per net while the analogous problem in graph drawing generally only involves pairs of vertices for each edge.

In addition, the placement and routing steps of electronic design automation (EDA) are similar in many ways to graph drawing, as is the problem of greedy embedding in distributed computing, and the graph drawing literature includes several results borrowed from the EDA literature. However, these problems also differ in several important ways: for instance, in EDA, area minimization and signal length are more important than aesthetics, and the routing problem in EDA may have more than two terminals per net while the analogous problem in graph drawing generally only involves pairs of vertices for each edge.

此外，电子设计自动化（EDA）Electronic Design Automation的布局和布线步骤在很多方面与图形绘制相似，而在分布式计算 Distributed Computing中贪婪嵌入 Greedy Embedding的问题也是如此，并且图形绘制文献包括从EDA文献中借来的一些结果。然而，这些问题也在几个重要方面有所不同: 例如，在 EDA，面积最小化和信号长度比美观更重要，EDA中的路由问题可能每个网有两个以上的终端，而图绘制中的类似问题通常只涉及每条边的顶点对。


Software 软件

图6：A graph drawing interface 一个画图软件界面(Gephi 0.9.1)

Software, systems, and providers of systems for drawing graphs include:

A graph drawing interface (Gephi 0.9.1)Software, systems, and providers of systems for drawing graphs include:

软件、系统和绘制图形系统的提供者包括:



  • BioFabric open-source software for visualizing large networks by drawing nodes as horizontal lines.

BioFabric 开源软件，用于将节点绘制为水平线来可视化大型网络。

  • Cytoscape, open-source software for visualizing molecular interaction networks

Cytoscape 可视化分子相互作用网络的开源软件

  • Gephi, open-source network analysis and visualization software

Gephi 开源网络分析和可视化软件

Graph-Tool 一个免费/免费的Python库，用于分析图形

Graphviz 来自美国电话电报公司的开放源码绘图系统

Linkurious 图形数据库的商业网络分析和可视化软件

  • Mathematica, a general purpose computation tool that includes 2D and 3D graph visualization and graph analysis tools.[25][26]

Mathematica 一个通用的计算工具，包括2D和3D图形可视化和图形分析工具。

Microsoft Automatic Graph Layout 用于图表布局的开放源码。net库(以前称为GLEE)

  • NetworkX is a Python library for studying graphs and networks.

NetworkX 用于研究图和网络的Python库

  • Tom Sawyer Software[28] Tom Sawyer Perspectives is graphics-based software for building enterprise-class graph and data visualization and analysis applications. It is a Software Development Kit (SDK) with a graphics-based design and preview environment.

Tom Sawyer Perspectives是一款基于图形的软件，用于构建企业级图形和数据可视化和分析应用程序。它是一个软件开发工具包(SDK)，具有基于图形的设计和预览环境

Tulip (software)开源数据可视化工具 yEd 具有图形布局功能的图形编辑器

  • yEd, a graph editor with graph layout functionality[30]

yEd 具有图形布局功能的图形编辑器

PGF/TikZ 带graphdrawing软件包的3.0（需要LuaTeX）

  • LaNet-vi, an open-source large network visualization software

LaNet-vi 开源大型网络可视化软件

  • Edraw Max 2D business technical diagramming software

Edraw Max 2D商业技术制图软件

考文献

Footnotes

Footnotes

脚注

  1. ↑ Di Battista et al. (1994), pp. vii–viii; Herman, Melançon & Marshall (2000), Section 1.1, "Typical Application Areas".
  2. ↑ 2.0 2.1 Di Battista et al. (1994), p. 6.
  3. ↑ 3.0 3.1 Di Battista et al. (1994), p. viii.
  4. ↑ Misue et al. (1995)
  5. ↑ Knuth, Donald E. (2013), "Two thousand years of combinatorics", in Wilson, Robin; Watkins, John J. (eds.), Combinatorics: Ancient and Modern, Oxford University Press, pp. 7–37.
  6. ↑ Holten & van Wijk (2009); Holten et al. (2011).
  7. ↑ Garg & Tamassia (1995).
  8. ↑ Longabaugh (2012).
  9. ↑ Di Battista et al. (1994), Section 2.1.2, Aesthetics, pp. 14–16; Purchase, Cohen & James (1997).
  10. ↑ Di Battista et al. (1994), p 14.
  11. ↑ Di Battista et al. (1994), p. 16.
  12. ↑ 12.0 12.1 Pach & Sharir (2009).
  13. ↑ Published in Grandjean, Martin (2014). "La connaissance est un réseau". Les Cahiers du Numérique. 10 (3): 37–54. doi:10.3166/lcn.10.3.37-54. Retrieved 2014-10-15.
  14. ↑ Di Battista et al. (1994), Section 2.7, "The Force-Directed Approach", pp. 29–30, and Chapter 10, "Force-Directed Methods", pp. 303–326.
  15. ↑ Beckman (1994); Koren (2005).
  16. ↑ Di Battista et al. (1994), Chapter 5, "Flow and Orthogonal Drawings", pp. 137–170; 模板:Harv.
  17. ↑ Herman, Melançon & Marshall (2000), Section 2.2, "Traditional Layout – An Overview".
  18. ↑ Sugiyama, Tagawa & Toda (1981); Bastert & Matuszewski (2001); Di Battista et al. (1994), Chapter 9, "Layered Drawings of Digraphs", pp. 265–302.
  19. ↑ Saaty (1964).
  20. ↑ Doğrusöz, Madden & Madden (1997).
  21. ↑ Di Battista et al. (1994), Section 4.7, "Dominance Drawings", pp. 112–127.
  22. ↑ Scott (2000); Brandes, Freeman & Wagner (2014).
  23. ↑ Di Battista et al. (1994), pp. 15–16, and Chapter 6, "Flow and Upward Planarity", pp. 171–214; Freese (2004).
  24. ↑ "Graphviz and Dynagraph – Static and Dynamic Graph Drawing Tools", by John Ellson, Emden R. Gansner, Eleftherios Koutsofios, Stephen C. North, and Gordon Woodhull, in Jünger & Mutzel (2004).
  25. ↑ GraphPlot Mathematica documentation
  26. ↑ Graph drawing tutorial
  27. ↑ Nachmanson, Robertson & Lee (2008).
  28. ↑ Madden et al. (1996).
  29. ↑ "Tulip – A Huge Graph Visualization Framework", by David Auber, in Jünger & Mutzel (2004).
  30. ↑ "yFiles – Visualization and Automatic Layout of Graphs", by Roland Wiese, Markus Eiglsperger, and Michael Kaufmann, in Jünger & Mutzel (2004).
  31. ↑ Tantau (2013); see also the older GD 2012 presentation

一般参考资料

citation|title=Drawing Graphs: Methods and Models|editor1-first=Michael|editor1-last=Kaufmann|editor2-first=Dorothea|editor2-last=Wagner|publisher=Springer-Verlag|series=Lecture Notes in Computer Science|volume=2025|year=2001|doi=10.1007/3-540-44969-8|isbn=978-3-540-42062-0}}. citation|editor-first=Roberto|editor-last=Tamassia|editor-link=Roberto Tamassia|title=Handbook of Graph Drawing and Visualization|publisher=CRC Press|url=http://cs.brown.edu/~rt/gdhandbook/%7Cyear=2014%7Caccess-date=2013-08-28%7Carchive-url=https://web.archive.org/web/20130815181243/http://cs.brown.edu/~rt/gdhandbook/%7Carchive-date=2013-08-15%7Curl-status=dead}}.

Specialized subtopics
  • Bachmaier, Christian; Brandes, Ulrik; Schreiber, Falk (2014), "Biological Networks", in Tamassia, Roberto (ed.), Handbook of Graph Drawing and Visualization, CRC Press, pp. 621–651.
  • Beckman, Brian (1994), Theory of Spectral Graph Layout, Tech. Report MSR-TR-94-04, Microsoft Research.
  • Brandes, Ulrik; Freeman, Linton C.; Wagner, Dorothea (2014), "Social Networks", in Tamassia, Roberto (ed.), Handbook of Graph Drawing and Visualization, CRC Press, pp. 805–839.
  • Di Battista, Giuseppe; Rimondini, Massimo (2014), "Computer Networks", in Tamassia, Roberto (ed.), Handbook of Graph Drawing and Visualization, CRC Press, pp. 763–803.
  • Misue, K.; Eades, P.; Lai, W.; Sugiyama, K. (1995), "Layout Adjustment and the Mental Map", Journal of Visual Languages and Computing, 6 (2): 183–210, doi:10.1006/jvlc.1995.1010.
  • Nachmanson, Lev; Robertson, George; Lee, Bongshin (2008), "Drawing Graphs with GLEE" (PDF), in Hong, Seok-Hee; Nishizeki, Takao; Quan, Wu (eds.), Graph Drawing, 15th International Symposium, GD 2007, Sydney, Australia, September 24–26, 2007, Revised Papers, Lecture Notes in Computer Science, vol. 4875, Springer-Verlag, pp. 389–394, doi:10.1007/978-3-540-77537-9_38, ISBN 978-3-540-77536-2 {{citation}}: Cite has empty unknown parameter: |1= (help).
  • Pach, János; Sharir, Micha (2009), "5.5 Angular resolution and slopes", Combinatorial Geometry and Its Algorithmic Applications: The Alcalá Lectures, Mathematical Surveys and Monographs, vol. 152, American Mathematical Society, pp. 126–127.
  • Tantau, Till (2013), "Graph Drawing in TikZ", Journal of Graph Algorithms and Applications, 17 (4): 495–513, doi:10.7155/jgaa.00301.

其他链接

  • GraphX library for .NET: open-source WPF library for graph calculation and visualization. Supports many layout and edge routing algorithms.
  • 模板:Dmoz for many additional links related to graph drawing.
取自“https://wiki.swarma.org/index.php?title=图的绘制_Graph_drawing&oldid=18727”