图动力系统

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
跳到导航 跳到搜索


在数学领域中， 图动态系统'Graph dynamical systems的概念可以用来捕捉发生在图或网络上的广泛的过程。Gds 数学和计算分析的一个主题是将它们的结构特性联系起来(如网络连接)和全球动力学的结果。

Gdss 的工作是研究有限图和有限状态空间。因此，研究通常涉及到的技术是图论，组合学，代数和动力系统，而不是微分几何。原则上，我们可以在一个无限图上定义和研究 gds (例如:。元胞自动机或概率元胞自动机在 [math]\displaystyle{ mathbb { z } ^ k }[/math]或相互作用的粒子系统(包括一些随机性)上，以及具有无限状态空间的 gds (例如:在耦合映象格子中的 [math]\displaystyle{ mathbb {r} }[/math]; 例如，见 Wu。[1]在下文中，除非另有说明，否则一切图和空间都默认为有限。

正式定义

图动力系统'Graph dynamical systems是由以下部分构成的:


  • 具有变量集v[Y] = {1,2, ... , n}的有限图 Y。根据上下文，可以为有向图或无向图。
  • Y的取自有限集合“K”的每个顶点v的状态，“系统状态”是“n”元组“x”= (x1, x2, ... , xn)，“x”[“v”]是由与垂直相关的状态组成的元组。
  • 每个顶点v的顶点函数fv 。顶点函数将时间“t”的顶点“v”的状态映射到时间t + 1 ，1基于与“Y”中“v”的1邻域相关的状态。
  • 一个“更新方案”，通过它可以实现对单个顶点状态的映射，从而得到一个映射为“F”的离散动力系统：“Kn”。


动力系统的相空间是有限有向图，其顶点集为 k n ，有向边(x，f (x))。相空间的结构由图 y 的性质、顶点函数(f i)i和更新方案决定。该领域的研究试图推断相空间特性的基础上的结构的系统组成。这种分析具有局部到全局的特点。

广义细胞自动机

例如，如果新方案由应用顶点函数组成，那么我们获得Generalized cellular automata (GCA) 广义细胞自动机(CA)类。在这种情况下，整体映射 f: k n → k n 是由

[math]\displaystyle{ f(x)vv(x[v]) }[/math]

这个类别被称为Generalized cellular automata (GCA) 广义细胞自动机，因为经典的或标准的细胞自动机通常定义和研究在正则图或网格上，并且我们通常假定顶点函数是相同的。


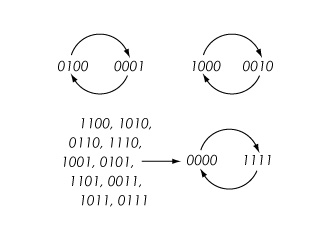
再例如: 设 y 是顶点{1,2,3,4}上的圆图，边{1,2} ，{2,3} ，{3,4}和{1,4} ，表示 Circ 子4 / 子。设 k {0,1}为每个顶点的状态空间，对所有顶点函数使用 nor 3</sub》: k 3→ k，该函数由 nor 子3 / sub (x，y，z)(1 + x)(1 + y)(1 + z)定义，算术模为2。然后，例如，使用同步更新将系统状态(0,1,0,0)映射到(0,0,0,1)。所有的相变都显示在下面的相空间中。


Circ-4-nor.jpg

序列动力系统

如果顶点函数按照 v [ y ]中 w (w 子1 / sub，w 子2 / sub，... ，w 子 m / sub)或置换数学 pi / math (math pi 1 / math，math pi 2， dots， pi n / math)指定的序列异步应用，那么我们可以得到' Sequential dynamical systems (SDS) 序列动力系统的类。[2]在这种情况下，可以方便地引入由顶点函数构造的 y 局部映射 f 子 i / 子

[math]\displaystyle{ F_i (x) = (x_1, x_2,\ldots, x_{i-1}, f_i(x[i]), x_{i+1}, \ldots , x_n) \;. }[/math]

Sds 映射 f [ f y ，w] : kn → k n 是复合函数


[math]\displaystyle{ [F_Y ,w] = F_{w(m)} \circ F_{w(m-1)} \circ \cdots \circ F_{w(2)} \circ F_{w(1)} \;. }[/math]


如果新序列是置换序列，那么我们就经常使用置换 SDS map F = [FY 以强调这一点。

例如: 设 y 是顶点{1,2,3,4}上的圆图，边{1,2} ，{2,3} ，{3,4}和{1,4} ，表示 Circ 子4 / 子。设 k {0,1}为每个顶点的状态空间，对所有顶点函数使用 nor 子3 / sub: k 3 → k，该函数由 nor 子3 / sub (x，y，z)(1 + x)(1 + y)(1 + z)定义，算术模为2。使用新序列(1,2,3,4) ，然后将系统状态(0,1,0,0)映射到(0,0,1,0)。在所有系统状态转换下，这个动力系统依次显示在下面的相空间。


Circ-4-nor-1234.jpg


随机图动力系统

例如，从应用程序的角度来看，思考 GDS的一个或多个组件包含随机元素的情况是有趣的。激励应用程序可以包括不完全理解的过程(例如:细胞内部的动力学) ，以及所有实际应用的某些方面似乎都符合某些概率分布。还有一些由确定性原理控制的应用程序，因为它们的描述要么复杂要么笨拙，所以考虑概率近似是有意义的。

图动力系统graph dynamical system的每个元素都可以通过几种方式随机化。例如，在顺序动力系统中，新序列可以是随机的。在每个迭代步骤中，可以从给定的新序列分布中随机选择具有相应概率的更新序列 w。新序列的匹配概率空间引出 SDS 地图的概率空间。在这方面需要研究的一个自然对象是 SDS 映射集合在状态空间上产生的 马尔可夫链Markov chain 。这种情况被称为新序列随机 GDS，其目的如，“事件”按照一定的速率随机发生的过程(如化学反应)，在并行计算 / 离散事件模拟中的同步，以及在后面描述的计算范例中的同步! ——确保这个交叉引用保持 / 工作。-->.


这个带有随机更新序列的具体例子说明了这类系统的两个一般事实: 当传递到一个 随机图动力系统Stochastic graph dynamical system时，一般会导致: (1)对 马尔可夫链Markov chain 的研究(其具体结构由 GDS 的组成部分控制) ，和(2)由此产生的 马尔可夫链Markov chain 趋向于具有指数数量的状态。随机 GDS 研究的一个中心目标是能够推导出简化模型。

我们也可以考虑顶点函数是随机的情况，即函数是随机的 GDS。例如，随机布尔网络是函数随机 GDS 使用同步更新方案的例子，其中状态空间为 k {0,1}。有限概率 细胞自动机（PCA)是功能随机 GDS 的另一个例子。原则上，相互作用粒子系统(IPS)包括有限和无限的 PCA，但实际上，IPS 的工作主要是关注无限的情况，因为这允许在状态空间中引入更多有趣的拓扑Topologies 。

应用

图动力系统是捕捉分布式系统(如生物网络和社会网络上的传染病)的自然框架，其中许多常常被称为 复杂系统Complex systems。

另请参见

参考文献

  1. ↑ Wu, Chai Wah (2005). "Synchronization in networks of nonlinear dynamical systems coupled via a directed graph". Nonlinearity. 18 (3): 1057–1064. Bibcode:2005Nonli..18.1057W. doi:10.1088/0951-7715/18/3/007.
  2. ↑ Mortveit, Henning S.; Reidys, Christian M. (2008). An introduction to sequential dynamical systems. Universitext. New York: Springer Verlag. ISBN 978-0-387-30654-4. 

延伸阅读

外部链接

编者推荐


本中文词条由水流心不竞 参与编译， CecileLi 审校，不是海绵宝宝编辑，欢迎在讨论页面留言。

本词条内容源自wikipedia及公开资料，遵守 CC3.0协议。

取自“https://wiki.swarma.org/index.php?title=图动力系统&oldid=18754”