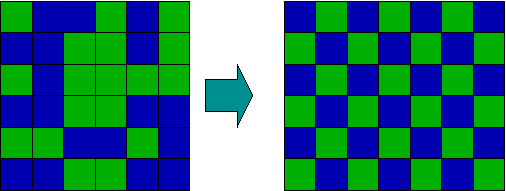
有序和无序
在物理学领域 Physics中,有序和无序指的是多粒子系统中某种对称性 symmetry或相关性 correlation的存在性问题。
在凝聚态物理学 condensed matter physics中,系统通常在低温下有序;受热后,它们会经历一个或几个相变 Phase Transition进入无序状态。
这种有序-无序转变的例子有:
- 冰的融化:固-液转变后,有序变无序;
- 铁在受到居里温度 Curie Temperature以上温度加热时就会逐渐退磁:铁磁性-顺磁性转变,磁有序变无序。
有序或无序的自由度可以是平移(晶体 crystal有序)、旋转(铁电性 ferroelectric有序)或自旋状态(磁 magnetic有序)。
这种顺序既可以是完全晶体空间群 space group的对称的也可以是关联的。根据相关系数随距离衰减的程度,我们可以说长程有序 long range order或短程有序 short range order。
如果一个无序的状态不存在于热力学平衡 thermodynamic equilibrium之中,那么就是淬致无序态。例如,玻璃 glass是通过淬火(过冷却 supercooling)液体获得的。推而广之,其它淬火态称为自旋玻璃态 spin glass、取向玻璃态 orientational glass。在某些情况下,淬致无序态的对立面是退火无序态。
特征化秩序 Characterizing order
晶格周期性与 x 射线结晶度 Lattice periodicity and X-ray crystallinity
固体中最严格的秩序形式是晶格周期性:某种模式( 即单元格 unit cell 中原子的排列)一次又一次地重复,通过平移形成一个不变的空间平铺 tiling。这就是晶体 crystal的定义属性。可能的对称性已在14个布拉维斯晶格 bravais lattice和230个空间群 space group中进行了分类。
格点周期性意味着长程有序:如果我们只知道一个单位单元,那么借助于平移对称性,就有可能在任意距离上精确地预测所有原子的位置。在20世纪的大部分时间里,相反的情况也被认为是合理的——但直到1982年准晶体 quasicrystal的发现表明,完全确定性的倾斜并不具有晶格周期性。
除了结构有序外,还有电荷有序 charge ordering、自旋有序 spin ordering、磁有序 magnetic ordering和成分有序。磁有序可以在中子衍射 neutron diffraction中观察到。
这是一个热力学'熵 Entropy的概念,通常表现为一个二阶相变 phase transition。一般来说,高热能与无序有关,低热能与有序有关,但有违背这一规律的现象存在。在低能衍射实验中,有序峰十分明显。
远程有序 Long-range order
远程有序描述了同一样本的远程部分表现出相关行为的物理系统。
这可以用相关函数 correlation function(量子场论)来表示,即旋转相关函数 spin-spin correlation Function(量子场论):
- [math]\displaystyle{ G(x,x') = \langle s(x),s(x') \rangle. \, }[/math]
其中 s 是自旋量子数,x 是特定系统中的距离函数。
当[math]\displaystyle{ x=x' }[/math]时,这个函数等于单位数量,当距离[math]\displaystyle{ |x-x'| }[/math]增加时,函数值减少。通常情况下,当它在很大程度上呈指数衰减 Decays Exponentially为零时,系统就被认为是无序的。但如果相关函数(量子场论)衰变为一个常数值,那么这个系统就被认为具有远程有序。如果它衰变成为零以作为距离的幂,那么它被称为准远程有序(详见下面引用的教科书第11章。参见Berezinskii–Kosterlitz–Thouless过渡 Berezinskii–Kosterlitz–Thouless Transition)。请注意,构成较大的[math]\displaystyle{ |x-x'| }[/math]的值可以理解为渐近性。
淬火无序态 Quenched disorder
在统计物理学 statistical physics中,当定义系统行为的某些参数是不随时间演化的随机变量时,系统称为淬火无序态。它们被淬火 quenched或者冷冻 frozen。自旋玻璃态 spin glass就是一个典型的例子。与退火无序态 annealed disorder相反,它允许随机变量的自我进化。
在数学中,由于热平均和噪声通常起着非常不同的作用,淬致无序比退火无序更难分析。事实上,这个问题太过困难以至于很少有已知的技术可以处理,而现有的大多数解决方案都依赖于近似值。最常用的是:
- 一种基于数学解析延拓的技术,被称为复制技巧 Replica Trick
- 谐振腔法 Cavity Method:虽然这些方法给出的结果与许多问题的实验结果相一致,但它们通常不是一个可证明的严格数学过程。
然而,最近人们已经通过严密的方法证明,至少在典型的自旋玻璃模型(所谓的 Sherrington–Kirkpatrick 模型 Sherrington–Kirkpatrick Model)中,基于复制的解确实是精确的。
该领域次常用的技术是生成函数分析 Generating Functional Analysis。这种方法是基于路线积分 Path Integrals的,虽然这通常比复制过程更难应用,但原则上是完全精确的,
退火无序态 Annealed disorder
当一个系统的某些参数进入其定义为随机变量时,称系统呈现退火无序态,但其演化与定义系统的自由度 Degrees of Freedom有关。它的定义与淬致无序相反,在淬灭无序态中,随机变量可能不会改变其值。
退火无序系统通常被认为更容易在数学上处理,因为无序系统的平均值和热平均值 thermal average可以在同一基础上处理。
参见
- 在高能物理学 High Energy Physics中,量子色动力学 Quantum Chromodynamics中手性凝聚物 Chiral Condensate的形成是一个有序转变,用超选择 Superselection来讨论
- 熵 Entropy
- 拓扑有序 Topological order
- 杂质 Impurity
- 上层建筑(物理学) superstructure (physics)
延伸阅读
- H Kleinert: Gauge Fields in Condensed Matter (, 2 volumes) Singapore: World Scientific (1989).
编者推荐
集智文章推荐
学科诞生记:凝聚态物理学的兴起
数十年以来,凝聚态物理学都是物理学领域中最大的分支,但是凝聚态物理学的成就直到最近才得以彰显。
本中文词条由小竹凉翻译,CecileLi审校,薄荷欢迎在讨论页面留言。
本词条内容源自公开资料,遵守 CC3.0协议。