二分图

此词条Jie初步翻译。由CecileLi初步审校。

无环二分图示例

m=5和n=3的完全二分图示例

 --趣木木（讨论）注意图的格式规范  查看之前发的表/链接页面 已改

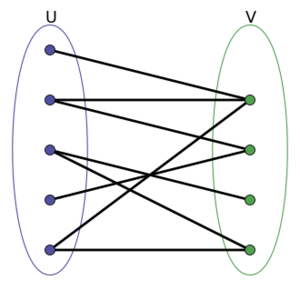
In the mathematical field of graph theory, a bipartite graph (or bigraph) is a graph whose vertices can be divided into two disjoint and independent sets [math]\displaystyle{ U }[/math] and [math]\displaystyle{ V }[/math] such that every edge connects a vertex in [math]\displaystyle{ U }[/math] to one in [math]\displaystyle{ V }[/math]. Vertex sets [math]\displaystyle{ U }[/math] and [math]\displaystyle{ V }[/math] are usually called the parts of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length。

In the mathematical field of graph theory, a bipartite graph (or bigraph) is a graph whose vertices can be divided into two disjoint and independent sets {\displaystyle U}U and {\displaystyle V}V such that every edge connects a vertex in {\displaystyle U}U to one in {\displaystyle V}V. Vertex sets {\displaystyle U}U and {\displaystyle V}V are usually called the parts of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles.[1][2]

在图论的数学领域中， 二分图Bipartite graph（或二部图）内的所有顶点可以分为两个互不相交且独立的集合U和集合V，并且邻边（无向或有向）的两个顶点分别属于集合U和集合V。通常集合U和集合V被称为该二分图的子集。同时，二分图中不包含任何形式的奇数环，即：集合U和集合V构造的点集所形成的循环圈边数不为奇数。

 --趣木木（讨论）变量斜体 已修改

The two sets [math]\displaystyle{ U }[/math] and [math]\displaystyle{ V }[/math] may be thought of as a coloring of the graph with two colors: if one colors all nodes in [math]\displaystyle{ U }[/math] blue, and all nodes in [math]\displaystyle{ V }[/math] green, each edge has endpoints of differing colors, as is required in the graph coloring problem.^[1]^[2] In contrast, such a coloring is impossible in the case of a non-bipartite graph, such as a triangle: after one node is colored blue and another green, the third vertex of the triangle is connected to vertices of both colors, preventing it from being assigned either color.

The two sets [math]\displaystyle{ U }[/math] and [math]\displaystyle{ V }[/math] may be thought of as a coloring of the graph with two colors: if one colors all nodes in [math]\displaystyle{ U }[/math] blue, and all nodes in [math]\displaystyle{ V }[/math] green, each edge has endpoints of differing colors, as is required in the graph coloring problem.^[2] In contrast, such a coloring is impossible in the case of a non-bipartite graph, such as a triangle: after one node is colored blue and another green, the third vertex of the triangle is connected to vertices of both colors, preventing it from being assigned either color.

通常可以将集合U和集合V视为被着色的两个图集：如果其中一个所有顶点为蓝色，另外一类为绿色，那么每条连边的两端必须具有不同的颜色。这是二分图必须满足的条件。相反，在非二分图（例如三角形）的情况下，这种着色要求是不可能的：因为如果一个顶点为蓝色，另一个为绿色，那么其剩下的第三个顶点将需要同时连接这两个颜色，显然这是不成立的，因为它违背了初始要求：二分图中所有顶点必须分为两个不相交且独立的集合U和V。即第三个顶点必须与另外两个点中的任意一个颜色相同。

One often writes [math]\displaystyle{ G=(U,V,E) }[/math] to denote a bipartite graph whose partition has the parts [math]\displaystyle{ U }[/math] and [math]\displaystyle{ V }[/math], with [math]\displaystyle{ E }[/math] denoting the edges of the graph. If a bipartite graph is not connected, it may have more than one bipartition;^[3] in this case, the [math]\displaystyle{ (U,V,E) }[/math] notation is helpful in specifying one particular bipartition that may be of importance in an application. If [math]\displaystyle{ |U|=|V| }[/math], that is, if the two subsets have equal cardinality, then [math]\displaystyle{ G }[/math] is called a balanced bipartite graph.^[1] If all vertices on the same side of the bipartition have the same degree, then [math]\displaystyle{ G }[/math] is called biregular.

One often writes [math]\displaystyle{ G=(U,V,E) }[/math] to denote a bipartite graph whose partition has the parts [math]\displaystyle{ U }[/math] and [math]\displaystyle{ V }[/math], with [math]\displaystyle{ E }[/math] denoting the edges of the graph. If a bipartite graph is not connected, it may have more than one bipartition;^[4] in this case, the [math]\displaystyle{ (U,V,E) }[/math] notation is helpful in specifying one particular bipartition that may be of importance in an application. If [math]\displaystyle{ |U|=|V| }[/math], that is, if the two subsets have equal cardinality, then [math]\displaystyle{ G }[/math] is called a balanced bipartite graph. If all vertices on the same side of the bipartition have the same degree, then [math]\displaystyle{ G }[/math] is called biregular.

对于二分图常用的表达方式是G=(U,V,E)，其中U和V分别代表顶点子集，E代表二分图中的连边。如果有一个二分图内部不连通，那么它可能具有多个二分图；在这种情况下，(U,V,E)标注将有助于指定一个特殊的二分图。在实际的应用当中这一点是很重要的。如果|U|=|V|，即这两个子集具有相同的基数，此时G被称为 均衡二分图Balanced bipartite graph。如果在二分图中同一侧（同一个子集）所有的顶点都具有相同的度数，则G被称为 双正则二分图Biregular。

Examples 案例

When modelling relations between two different classes of objects, bipartite graphs very often arise naturally. For instance, a graph of football players and clubs, with an edge between a player and a club if the player has played for that club, is a natural example of an affiliation network, a type of bipartite graph used in social network analysis.

When modelling relations between two different classes of objects, bipartite graphs very often arise naturally. For instance, a graph of football players and clubs, with an edge between a player and a club if the player has played for that club, is a natural example of an affiliation network, a type of bipartite graph used in social network analysis.

在建立两类不同对象之间的关系时，人们常常会很自然地选择二分图。以建立足球运动员和俱乐部的关系图为例，如果该球员曾为该俱乐部效力，那么在运动员和俱乐部之间就形成了一条边。这是二分图在建立隶属关系网络中的应用示例。在社交网络分析中，隶属关系便形成一种二分图。

Another example where bipartite graphs appear naturally is in the (NP-complete) railway optimization problem, in which the input is a schedule of trains and their stops, and the goal is to find a set of train stations as small as possible such that every train visits at least one of the chosen stations. This problem can be modeled as a dominating set problem in a bipartite graph that has a vertex for each train and each station and an edge for each pair of a station and a train that stops at that station.[7]

自觉选用二分图的另一个例子是（NP-完全问题）铁路优化问题，其中输入项是火车的时间表及其停靠点，目标是找到尽可能小的火车站集合，以便每个火车都可以停靠至少一个选定的火车站。我们可以运用建模将这个问题转化为一个二分图中的主导集合问题，该图中每辆列车和每个车站都被看作是一个顶点，而当某列车停靠在某车站的时候，它们所形成的关系可看作一条连边。

A third example is in the academic field of numismatics. Ancient coins are made using two positive impressions of the design (the obverse and reverse). The charts numismatists produce to represent the production of coins are bipartite graphs.^[5]

A third example is in the academic field of numismatics. Ancient coins are made using two positive impressions of the design (the obverse and reverse). The charts numismatists produce to represent the production of coins are bipartite graphs.

第三个例子涉及到货币金融学领域。古代的硬币被设计为正反两面，不同时期和地区的政府会使用不同的正反面组合，因此，将所有可能的组合画成图就是一个二分图的结构。

More abstract examples include the following:

更多抽象的例子:

Every tree is bipartite.^[2]
每个树状图都是二分的。

Cycle graphs with an even number of vertices are bipartite.^[2]
具有偶数个顶点的环图都是二分的

Every planar graph whose faces all have even length is bipartite. Special cases of this are grid graphs and squaregraphs, in which every inner face consists of 4 edges and every inner vertex has four or more neighbors.
在平面图中，所有面都具有偶数条边，该图为二分图。特殊情况是网格图和方图，其中每个内面都有4个边，每个内顶点至少有4个相邻点。

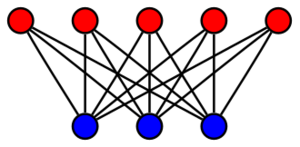
The complete bipartite graph on m and n vertices, denoted by K_n,m is the bipartite graph [math]\displaystyle{ G = (U, V, E) }[/math], where U and V are disjoint sets of size m and n, respectively, and E connects every vertex in U with all vertices in V. It follows that K_m,n has mn edges.
在一个完全二分图中，分别由m和n的顶点（用Km,n表示）组成的两个不相交的集合U和V，连边E由分别在集合U和V的两个顶点连接。该二分图表示为G =（U，V，E），并且具有mn条边。另外完全二分图还有一个特例，那就是 冠图Crown graphs。冠图是将一个完全二分图中所有的完美匹配连边去掉后形成的。

Hypercube graphs, partial cubes, and median graphs are bipartite. In these graphs, the vertices may be labeled by bitvectors, in such a way that two vertices are adjacent if and only if the corresponding bitvectors differ in a single position. A bipartition may be formed by separating the vertices whose bitvectors have an even number of ones from the vertices with an odd number of ones. Trees and squaregraphs form examples of median graphs, and every median graph is a partial cube.

超立方体图Hypercube graph， 局部立方体Partial cube和 中位数图Median graph均为二分图。判别方法是将这些图中的顶点用 位向量Bitvector（二进制位组成的向量）进行标记，然后对比其中两个顶点的位向量，发现当且仅当位向量中只有一个位元是不同的时候，该两个顶点相邻。另外判定该图的二分性可以通过观察每个顶点的位向量，奇数位向量和偶数位向量分别为该图的二分顶点子集。树状图和方图都是中位数图，而所有中位数图都是局部立方体。

Properties 属性

Characterization 特征表述

Bipartite graphs may be characterized in several different ways:

二分图可以用以下几种不同的方式来描述其特征：

A graph is bipartite if and only if it does not contain an odd cycle. Theorem 2.1.3, p. 8. Asratian et al. attribute this characterization to a 1916 paper by Dénes Kőnig. For infinite graphs, this result requires the axiom of choice.
当且仅当它不包含奇数环的时候，该图为二分图。（定理 2.1.3，p.8.Asratian 等人将这种描述归因于 Dénes Kőnig 的 1916 年论文。对于无限图，这个结果需要公理选择。）

A graph is bipartite if and only if it is 2-colorable, (i.e. its chromatic number is less than or equal to 2).
当且仅当图是2色系图2-colorable（即，其色数小于或等于2，详见“图着色”）时，该图为二分图。

The spectrum of a graph is symmetric if and only if it's a bipartite graph.
当且仅当它是二分图时，图的频谱是对称的。

Kőnig's theorem and perfect graphs 柯尼希定理和完美图

In bipartite graphs, the size of minimum vertex cover is equal to the size of the maximum matching; this is Kőnig's theorem.[16][17] An alternative and equivalent form of this theorem is that the size of the maximum independent set plus the size of the maximum matching is equal to the number of vertices. In any graph without isolated vertices the size of the minimum edge cover plus the size of a maximum matching equals the number of vertices.[18] Combining this equality with Kőnig's theorem leads to the facts that, in bipartite graphs, the size of the minimum edge cover is equal to the size of the maximum independent set, and the size of the minimum edge cover plus the size of the minimum vertex cover is equal to the number of vertices.

在二分图中， 最小顶点覆盖Minimum vertex cover（顶点数）等于 最大匹配数Maximum matching(边数)；这就是 柯尼希定理Kőnig's theorem。该定理的另一种等价形式是， 最大独立集Maximum independent set（顶点数）加上最大匹配数等于顶点的数量。在任意没有孤立顶点的图中， 最小边覆盖Minimum edge cover（边数）加上最大匹配数等于顶点数。于是，将以上等式与柯尼希定理相结合，得出以下事实：在二分图中，最小边覆盖数值等于最大独立集数值，最小边覆盖数值加上最小顶点覆盖数值等于顶点数。

Another class of related results concerns perfect graphs: every bipartite graph, the complement of every bipartite graph, the line graph of every bipartite graph, and the complement of the line graph of every bipartite graph, are all perfect. Perfection of bipartite graphs is easy to see (their chromatic number is two and their maximum clique size is also two) but perfection of the complements of bipartite graphs is less trivial, and is another restatement of Kőnig's theorem. This was one of the results that motivated the initial definition of perfect graphs.

另一类相关特性与 完美图Perfect graph有关：每个二分图及其补图、线图、线图的补图均为完美图。其实关于二分图的完美性很容易就可以看出来（它们的色数为2，最大的团数同样为2），但是二分图的补图完美性的判定更简单些，且可以看作是柯尼希定理的另一种表述。其实在定义完美图这一概念的初期，它是作为其中之一的论证结果而存在的。同时完美图线图的补图完美性也是作为柯尼希定理的另一种表述，线图的完美性陈述了比较早期的柯尼希定理，即每一个二分图的着色边，其色数都等于其最大节点度数。

According to the strong perfect graph theorem, the perfect graphs have a forbidden graph characterization resembling that of bipartite graphs: a graph is bipartite if and only if it has no odd cycle as a subgraph, and a graph is perfect if and only if it has no odd cycle or its complement as an induced subgraph. The bipartite graphs, line graphs of bipartite graphs, and their complements form four out of the five basic classes of perfect graphs used in the proof of the strong perfect graph theorem.

根据 强完美图定理Strong perfect graph theorem，完美图具有类似于二分图的 禁止图特征Forbidden graph characterization：当且仅当它没有奇环的子图时，图才是二分的；当且仅当它没有奇环或其补图作为 导出子图Induced subgraph时，图才是完美的。二分图及其线图、补图占据了完美图五种基本类别中的四个，它们可以用于证明了强完美图定理。

Degree 度

For a vertex, the number of adjacent vertices is called the degree of the vertex and is denoted [math]\displaystyle{ \deg(v) }[/math].

对于一个顶点，其相邻顶点的数量称为该顶点的度数，并表示为deg（v）。二分图的总度数和公式为：

{\displaystyle \sum _{v\in V}\deg(v)=\sum _{u\in U}\deg(u)=|E|\,.}\sum_{v \in V} \deg(v) = \sum_{u \in U} \deg(u) = |E|\, .

The degree sequence of a bipartite graph is the pair of lists each containing the degrees of the two parts [math]\displaystyle{ U }[/math] and [math]\displaystyle{ V }[/math]. For example, the complete bipartite graph K_3,5 has degree sequence [math]\displaystyle{ (5,5,5),(3,3,3,3,3) }[/math]. Isomorphic bipartite graphs have the same degree sequence. However, the degree sequence does not, in general, uniquely identify a bipartite graph; in some cases, non-isomorphic bipartite graphs may have the same degree sequence.

一个二分图的度数序列是一对列表，每个列表包含两个部分U和V的度数。例如，完全二分图K3,5具有度数序列（5,5,5），（3,3,3,3,3）。其 同构二分图Isomorphic bipartite graphs具有相同的度数序列。但是，度数序列通常不是定义二分图的唯一方法；在某些情况下，非同构二分图可能具有相同的度数序列。

The bipartite realization problem is the problem of finding a simple bipartite graph with the degree sequence being two given lists of natural numbers. (Trailing zeros may be ignored since they are trivially realized by adding an appropriate number of isolated vertices to the digraph.)

二分实现问题Bipartite realization problem是通过已知的两组自然数序列作为度数序列，来查找简单的二分图的判定问题（数理逻辑）。（尾随零可以忽略，因为通过向图添加适当数量的孤立顶点可以轻松实现尾随零。）

 --趣木木（讨论）注意全文是否大写专业名词的首字母  已修改

Relation to hypergraphs and directed graphs 与超图和有向图的关系

The biadjacency matrix of a bipartite graph [math]\displaystyle{ (U,V,E) }[/math] is a (0,1) matrix of size [math]\displaystyle{ |U|\times|V| }[/math] that has a one for each pair of adjacent vertices and a zero for nonadjacent vertices.^[6] Biadjacency matrices may be used to describe equivalences between bipartite graphs, hypergraphs, and directed graphs.

The biadjacency matrix of a bipartite graph [math]\displaystyle{ (U,V,E) }[/math] is a (0,1) matrix of size [math]\displaystyle{ |U|\times|V| }[/math] that has a one for each pair of adjacent vertices and a zero for nonadjacent vertices. Biadjacency matrices may be used to describe equivalences between bipartite graphs, hypergraphs, and directed graphs.

一个二分图（U，V，E）的双邻矩阵是大小为|V| 的（0,1）矩阵，其分别代表了每对相邻顶点集合和非相邻顶点的集合（全零矩阵）。双邻接矩阵可用于描述二分图，超图和定向图之间的等价关系。

A hypergraph is a combinatorial structure that, like an undirected graph, has vertices and edges, but in which the edges may be arbitrary sets of vertices rather than having to have exactly two endpoints. A bipartite graph [math]\displaystyle{ (U,V,E) }[/math] may be used to model a hypergraph in which $U$ is the set of vertices of the hypergraph, $V$ is the set of hyperedges, and $E$ contains an edge from a hypergraph vertex $v$ to a hypergraph edge $e$ exactly when $v$ is one of the endpoints of $e$ . Under this correspondence, the biadjacency matrices of bipartite graphs are exactly the incidence matrices of the corresponding hypergraphs. As a special case of this correspondence between bipartite graphs and hypergraphs, any multigraph (a graph in which there may be two or more edges between the same two vertices) may be interpreted as a hypergraph in which some hyperedges have equal sets of endpoints, and represented by a bipartite graph that does not have multiple adjacencies and in which the vertices on one side of the bipartition all have degree two.^[7]

A hypergraph is a combinatorial structure that, like an undirected graph, has vertices and edges, but in which the edges may be arbitrary sets of vertices rather than having to have exactly two endpoints. A bipartite graph [math]\displaystyle{ (U,V,E) }[/math] may be used to model a hypergraph in which is the set of vertices of the hypergraph, is the set of hyperedges, and contains an edge from a hypergraph vertex to a hypergraph edge exactly when is one of the endpoints of . Under this correspondence, the biadjacency matrices of bipartite graphs are exactly the incidence matrices of the corresponding hypergraphs. As a special case of this correspondence between bipartite graphs and hypergraphs, any multigraph (a graph in which there may be two or more edges between the same two vertices) may be interpreted as a hypergraph in which some hyperedges have equal sets of endpoints, and represented by a bipartite graph that does not have multiple adjacencies and in which the vertices on one side of the bipartition all have degree two.

超图是一种组合结构，类似于无向图，它具有顶点和连边，但是其中的边可以是任意子集组的顶点，而不必具有两个端点。可以使用二分图（U，V，E）来建模超图，其中U是超图的其中一个顶点集，V是该超图的连边集（称为超边集），E包含的连边定义为：从一个超图顶点v到超图连边e恰好当v是e的端点集之一时。在这种对应关系下，二分图的双邻矩阵正好是其相应超图的关联矩阵。作为二分图和超图之间这种对应关系的特例，任何 多重图Multigraph（即在相同两点之间可能存在的多条边的图）都可以解释为其中一些超边具有相同端点集的超图，并且由不具有多个邻接关系的二分图表示，其中二分图的同边顶点的度均为2。

A similar reinterpretation of adjacency matrices may be used to show a one-to-one correspondence between directed graphs (on a given number of labeled vertices, allowing self-loops) and balanced bipartite graphs, with the same number of vertices on both sides of the bipartition. For, the adjacency matrix of a directed graph with $n$ vertices can be any (0,1) matrix of size [math]\displaystyle{ n\times n }[/math], which can then be reinterpreted as the adjacency matrix of a bipartite graph with $n$ vertices on each side of its bipartition.

A similar reinterpretation of adjacency matrices may be used to show a one-to-one correspondence between directed graphs (on a given number of labeled vertices, allowing self-loops) and balanced bipartite graphs, with the same number of vertices on both sides of the bipartition. For, the adjacency matrix of a directed graph with vertices can be any (0,1) matrix of size [math]\displaystyle{ n\times n }[/math], which can then be reinterpreted as the adjacency matrix of a bipartite graph with vertices on each side of its bipartition.

关于 邻接矩阵Adjacency matrices的另一个相似解释可以被用于展示有向图和均衡二分图（二分子集顶点数相等）之间的一一对应关系（在给定数量的标记顶点上，允许自循环）。例如，具有n个顶点的有向图的邻接矩阵可以是大小为n×n的任何（0,1）矩阵，然后可以将其重新解释为：具有相同顶点数n的同边子集的二分图的邻接矩阵。通过这种构建方式，二分图可以被解释为是一个有向图的 二分双重覆盖Bipartite double cover。

Algorithms 算法

Testing bipartiteness 二分性测试

It is possible to test whether a graph is bipartite, and to return either a two-coloring (if it is bipartite) or an odd cycle (if it is not) in linear time, using depth-first search. The main idea is to assign to each vertex the color that differs from the color of its parent in the depth-first search forest, assigning colors in a preorder traversal of the depth-first-search forest. This will necessarily provide a two-coloring of the spanning forest consisting of the edges connecting vertices to their parents, but it may not properly color some of the non-forest edges. In a depth-first search forest, one of the two endpoints of every non-forest edge is an ancestor of the other endpoint, and when the depth first search discovers an edge of this type it should check that these two vertices have different colors. If they do not, then the path in the forest from ancestor to descendant, together with the miscolored edge, form an odd cycle, which is returned from the algorithm together with the result that the graph is not bipartite. However, if the algorithm terminates without detecting an odd cycle of this type, then every edge must be properly colored, and the algorithm returns the coloring together with the result that the graph is bipartite.

可以使用 深度优先搜索Depth-first search来测试图是否为二分图，并在线性时间内返回双色（如果是二分图）或奇数环（如果不是二分图）。其方法的主要思想是为每个顶点分配与 深度优先搜索林Depth-first search forest中其父级颜色不同的颜色，并在其中进行遍历。这必定会为 生成森林Spanning forest提供两种颜色，包括将顶点连接到其父级的边。不过它可能无法为非森林边正确着色。在深度优先搜索林中，每个非林边缘的两个顶点之一是另一个顶点的祖先，并且当深度优先搜索发现这种类型的边时，应检查这两个顶点是否具有不同的颜色。如果不是，则森林中从祖先到后代的路径与颜色不同的边一起会形成一个奇数环，该奇数环会从算法中返回，并输出非二分图的结果。但是，如果算法在未检测到此类奇数环的情况下终止，则必须对每个边进行适当的着色，并返回双色以及该图形为二分图的结果。

Alternatively, a similar procedure may be used with breadth-first search in place of depth-first search. Again, each node is given the opposite color to its parent in the search forest, in breadth-first order. If, when a vertex is colored, there exists an edge connecting it to a previously-colored vertex with the same color, then this edge together with the paths in the breadth-first search forest connecting its two endpoints to their lowest common ancestor forms an odd cycle. If the algorithm terminates without finding an odd cycle in this way, then it must have found a proper coloring, and can safely conclude that the graph is bipartite.

又或者，可以使用 广度优先搜索Breadth-first search来替代深度优先搜索进行检测。同样，在搜索林中，以广度优先的顺序为每个节点赋予与父级节点相反的颜色。如果在着色某个顶点时存在一条边，其连接了与先前着色的顶点相同的颜色。然后这条边沿着以广度优先搜索林中的路径，将其两个端点与其 最低共有祖先Lowest common ancestor相连，形成一条奇数环。当然，如果该算法最终没找到奇数环且终止，那么它肯定已经找到了正确的着色，可以安全返回并得出该图是二分图的结论。

For the intersection graphs of [math]\displaystyle{ n }[/math] line segments or other simple shapes in the Euclidean plane, it is possible to test whether the graph is bipartite and return either a two-coloring or an odd cycle in time [math]\displaystyle{ O(n\log n) }[/math], even though the graph itself may have up to [math]\displaystyle{ O(n^2) }[/math] edges.

对于n个线段的相交图或 欧几里得平面Euclidean plane中的其他简单形状图，即使图本身可能具有多达O(n²)个边缘，也可以测试其是否而二分图，并在时间O(nlogn)中返回双色（判定为二分图）或奇数环（判定为非二分图）。

Odd cycle transversal 奇环横贯

Odd cycle transversal is an NP-complete algorithmic problem that asks, given a graph G = (V,E) and a number k, whether there exists a set of k vertices whose removal from G would cause the resulting graph to be bipartite.[27] The problem is fixed-parameter tractable, meaning that there is an algorithm whose running time can be bounded by a polynomial function of the size of the graph multiplied by a larger function of k.[28] The name odd cycle transversal comes from the fact that a graph is bipartite if and only if it has no odd cycles. Hence, to delete vertices from a graph in order to obtain a bipartite graph, one needs to "hit all odd cycle", or find a so-called odd cycle transversal set. In the illustration, every odd cycle in the graph contains the blue (the bottommost) vertices, so removing those vertices kills all odd cycles and leaves a bipartite graph.

奇环横贯是一个 NP完全算法问题NP-complete algorithmic problem（因不能用多项式算法而使问题无法解决的），在给定图形G =（V，E）和数字k的情况下，询问是否存在一组k个顶点，将其从G移除会导致生成为二分图。这个问题是 固定参数可解Fixed-parameter tractable的，这意味着存在一种算法，其运行时间可以由图形大小的多项式函数乘以增大系数k来确定。奇环横贯的名称源于：当且仅当图没有奇数环时，该图是二分图。因此，为了从图中删除顶点来获得二分图，就需要“命中所有奇数环”或找到所谓的奇环横贯集合。例如在图示中，图中的每个奇数环都包含蓝色（最底部）顶点，因此删除这些顶点就相当于删除了所有奇数环并留下一个二分图。

The edge bipartization problem is the algorithmic problem of deleting as few edges as possible to make a graph bipartite and is also an important problem in graph modification algorithmics. This problem is also fixed-parameter tractable, and can be solved in time, where k is the number of edges to delete and m is the number of edges in the input graph.

The edge bipartization problem is the algorithmic problem of deleting as few edges as possible to make a graph bipartite and is also an important problem in graph modification algorithmics. This problem is also fixed-parameter tractable, and can be solved in time, where k is the number of edges to delete and m is the number of edges in the input graph.

边二分化问题Edge bipartization problem是删除尽可能少的边以使其成为二分图的问题，也是图修改算法中的重要问题。此问题同样是固定参数可解的，可以在时间O(2k m2),内解决，其中k是要删除的边数，m是输入图中的边数。

Matching 匹配

A matching in a graph is a subset of its edges, no two of which share an endpoint. Polynomial time algorithms are known for many algorithmic problems on matchings, including maximum matching (finding a matching that uses as many edges as possible), maximum weight matching, and stable marriage.In many cases, matching problems are simpler to solve on bipartite graphs than on non-bipartite graphs,[31] and many matching algorithms such as the Hopcroft–Karp algorithm for maximum cardinality matching[32] work correctly only on bipartite inputs.

一个图中的匹配是其边集的一个子集，其中任意两个边均不共享一个端点。 多项式时间算法Polynomial time algorithms素以解决很多关于匹配的算法问题而得名，包括 最大匹配Maximum matching（查找使用尽可能多的边的匹配）， 最大权重匹配Maximum weight matching和 稳定婚姻问题Stable marriage。在许多情况下，与非二分图相比，二分图上的匹配问题更容易解决，并且许多匹配算法（例如用于最大基数匹配的 Hopcroft-Karp算法）仅在二分图输入的时候才能正确运行。

As a simple example, suppose that a set [math]\displaystyle{ P }[/math] of people are all seeking jobs from among a set of [math]\displaystyle{ J }[/math] jobs, with not all people suitable for all jobs. This situation can be modeled as a bipartite graph [math]\displaystyle{ (P,J,E) }[/math] where an edge connects each job-seeker with each suitable job.^[8] A perfect matching describes a way of simultaneously satisfying all job-seekers and filling all jobs; Hall's marriage theorem provides a characterization of the bipartite graphs which allow perfect matchings. The National Resident Matching Program applies graph matching methods to solve this problem for U.S. medical student job-seekers and hospital residency jobs.

As a simple example, suppose that a set [math]\displaystyle{ P }[/math] of people are all seeking jobs from among a set of [math]\displaystyle{ J }[/math] jobs, with not all people suitable for all jobs. This situation can be modeled as a bipartite graph [math]\displaystyle{ (P,J,E) }[/math] where an edge connects each job-seeker with each suitable job. A perfect matching describes a way of simultaneously satisfying all job-seekers and filling all jobs; Hall's marriage theorem provides a characterization of the bipartite graphs which allow perfect matchings. The National Resident Matching Program applies graph matching methods to solve this problem for U.S. medical student job-seekers and hospital residency jobs.

举一个简单的例子，假设一组P的所有人都在一组J的职位中寻找工作，但并不是所有人都适合所有职位。可以将这种情况建模为一个二分图（P，J，E），其中当每个求职者找到其合适的工作时产生的关系就作为连边。一个完美的匹配描述的是所有求职者同时找到所有工作的情况； 霍尔的婚姻定理Hall's marriage theorem阐述的就是二分图允许完美匹配的特征。美国国民住院医师匹配项目采用的就是图形匹配法来解决美国医学生求职者和医院实习工作的匹配问题。

The Dulmage–Mendelsohn decomposition is a structural decomposition of bipartite graphs that is useful in finding maximum matchings.^[9]

The Dulmage–Mendelsohn decomposition is a structural decomposition of bipartite graphs that is useful in finding maximum matchings.

Dulmage–Mendelsohn 分解是二分图的结构分解，可用于寻找最大匹配。

Additional applications 其他应用

Bipartite graphs are extensively used in modern coding theory, especially to decode codewords received from the channel. Factor graphs and Tanner graphs are examples of this. A Tanner graph is a bipartite graph in which the vertices on one side of the bipartition represent digits of a codeword, and the vertices on the other side represent combinations of digits that are expected to sum to zero in a codeword without errors.

二分图在现代编码理论中被广泛使用，尤其是对从通道接收到的密码进行解码。例如 因子图Factor graphs和 坦纳图Tanner graphs。Tanner图是二分图，其中二分的一侧顶点表示一个密码数字，另一侧顶点表示一个数字的组合，这些数字的总和期望为零且不存在误差。因子图与置信网络密切相关，用于LDPC和Turbo码的概率解码。

In computer science, a Petri net is a mathematical modeling tool used in analysis and simulations of concurrent systems. A system is modeled as a bipartite directed graph with two sets of nodes: A set of "place" nodes that contain resources, and a set of "event" nodes which generate and/or consume resources. There are additional constraints on the nodes and edges that constrain the behavior of the system. Petri nets utilize the properties of bipartite directed graphs and other properties to allow mathematical proofs of the behavior of systems while also allowing easy implementation of simulations of the system.

在计算机科学中， Petri网是用于分析和模拟并发系统的数学建模工具。该系统被建模为具有两组点集的二分有向图：一组“库所”点集用于容纳资源，以及一组“事件”点集用于生成和（或）消耗资源。他们通过约束节点和连边的传递来进一步限制系统的行为。Petri网利用二分有向图的属性和其他属性来允许对系统行为进行数学证明，同时还可以轻松实现系统仿真。

In projective geometry, Levi graphs are a form of bipartite graph used to model the incidences between points and lines in a configuration. Corresponding to the geometric property of points and lines that every two lines meet in at most one point and every two points be connected with a single line, Levi graphs necessarily do not contain any cycles of length four, so their girth must be six or more.

在射影几何中， Levi图是二分图的一种形式，用于对配置点和线之间的入射进行建模。对应于点和线的几何特性，即每两条线最多相交一个点，并且每两个点都由一条线连接，因此Levi图不一定包含任何长度为4的环，进而其周长必须为6或更大。

References 参考文献

↑ ^1.0 ^1.1 Asratian, Denley & Häggkvist (1998), p. 7.
↑ ^2.0 ^2.1 ^2.2 ^2.3 | year = 2012}}. 引用错误：无效<ref>标签；name属性“s12”使用不同内容定义了多次
↑ , 2008 {{citation}}: Missing or empty |title= (help).
↑ , 2008 {{citation}}: Missing or empty |title= (help).
↑ Bracey, Robert (2012). "On the Graphical Interpreation of Herod's Coinage in Judaea and Rome in Coins". pp. 65–84.
↑ Asratian, Denley & Häggkvist (1998), p. 17.
↑ 模板:SpringerEOM
↑ Ahuja, Magnanti & Orlin (1993), Application 12.1 Bipartite Personnel Assignment, pp. 463–464.
↑ Dulmage & Mendelsohn (1958).

External links 相关链接

模板:Springer
《图，二分图》，Encyclopedia of Mathematics, EMS Press, 2001 [1994]

Information System on Graph Classes and their Inclusions: bipartite graph
《图类及其包含的信息系统：二分图》

模板:Mathworld
《二分图》，Weisstein, Eric W，MathWorld.

Bipartite graphs in systems biology and medicine
《系统生物学和医学中的二分图》

Category:Graph families

类别: 图族

Category:Parity (mathematics)

分类: 奇偶校验(数学)

This page was moved from wikipedia:en:Bipartite graph. Its edit history can be viewed at 二分图/edithistory

[adh98-7-1] 1.0 ^1.1 Asratian, Denley & Häggkvist (1998), p. 7.

[s12-2] 2.0 ^2.1 ^2.2 ^2.3 | year = 2012}}. 引用错误：无效<ref>标签；name属性“s12”使用不同内容定义了多次

[3] , 2008 {{citation}}: Missing or empty |title= (help).

[4] , 2008 {{citation}}: Missing or empty |title= (help).

[bracey2012-5] Bracey, Robert (2012). "On the Graphical Interpreation of Herod's Coinage in Judaea and Rome in Coins". pp. 65–84.

[6] Asratian, Denley & Häggkvist (1998), p. 17.

[7] 模板:SpringerEOM

[8] Ahuja, Magnanti & Orlin (1993), Application 12.1 Bipartite Personnel Assignment, pp. 463–464.

[9] Dulmage & Mendelsohn (1958).

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

二分图

目录