路径 path
在图论 Graph theory中,图中的路径 path是一个有限或无限的边序列,这些边连接着一系列顶点,这些顶点在大多数定义中都是不同的(又因为这些顶点是不同的,所以图中的边也是不同的)。有向图 directed path(有时也称为dipath[1])中的有向路径,在具有附加条件:所有的边都方向相同时是一个有限或无限的边序列,它连接一系列不同的顶点。
路径是图论的基本概念,在大多数图论文本的导论部分都有描述,见Bondy and Murty(1976) , Gibbons(1985),或Diestel(2005)。 Korte(1990)等人著作中,涵盖了更多关于图中路径的高级算法的话题。
定义
步道 轨迹 路径 Walk, trail, path
- 步道 Walk:是连接一系列顶点形成的有限或无限的边序列。
- 以一个图为例 G = ( V, E, ϕ ) 。有限步道 finite walk是一系列的边 ( e1, e2, …, en − 1 ),其顶点序列( v1, v2, …, vn ) 。 ϕ ( ei ) = {vi, vi + 1}对于i = 1, 2, …, n − 1。 ( v1, v2, …, vn ) 是移动的顶点序列。如果 v1 = vn ,则此步道封闭,反之则开放。无限步道 infinite walk是由一系列边组成的,它们的类型与这里描述的相同,但没有起点或终点,而一个半无限步道(或光线)则有起点但是没有终点。
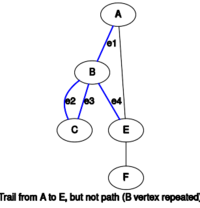
- 轨迹 trail是所有的边缘都清晰可见的步道。
- 路径 path是一条所有顶点(包括所有边)都是不同的轨迹。
如果 w = ( e1, e2, …, en − 1 )是有顶点的序列 (v1, v2, …, vn),那么w 就是从 v1 到 vn的有限步道。同样,对于一条轨迹或者一条路径也是如此。如果两个不同的顶点之间有一个有限步道,那么在它们之间也有一条有限的轨迹和一条有限的路径。
有些学者对路径的定义中并不要求它的所有顶点都是不同的,而是使用术语“简单路径”来指代这样的路径。
一个加权图 weighted graph将一个值(权重)与图中的每条边相关联。一个加权图中的步道(或轨迹或路径)的权是所有边的权之和。有时,“成本 cost”或“长度 length”这两个词可以用来指代“权重”这一概念。
有向的步道,轨迹,路径 Directed walk, trail, path
- 有向步道 directed walk是指由连接一系列顶点的边沿相同方向定向形成的有限或无限序列。
- 以一个有向图 G = ( V, E, ϕ ) 为例。有限有向步道由一系列的边组成 ( e1, e2, …, en − 1 ),而对于这些边,又存在一系列的顶点 ( v1, v2, …, vn )。 ϕ ( ei ) = ( vi, vi + 1 )对于 i = 1, 2, …, n − 1 。( v1, v2, …, vn )是有向步道的顶点序列。无限有向步道是一个边序列,其类型与本文描述的相同,但起点或终点,而半无限有向步道(或射线)有起点,但没有终点。
- 有向轨迹 directed trail是指所有边都可见的轨迹。
- 有向路径 directed path是指所有顶点都不同的有向路径。
假设一个步道 w = ( e1, e2, …, en − 1 )是顶点序列有限的( v1, v2, …, vn )有向步道,那么w就是从 v1 到 vn的步道。同样,对于有向轨迹或路径也是如此。如果在两个不同的顶点之间存在有限有向步道,那么在它们之间也存在有限有向轨迹和有限有向路径。
有些学者并不要求有向路径的所有顶点都是不同的,因此他们用“简单有向路径 simple directed path”这个术语来表示它。
一个加权有向图将一个值(权重)与有向图中的每条边相关联。加权有向图中有向步道(或路径)的权是有向边权重的和。有时,“成本 cost”或“长度 length”这两个词可以用来指代“权重”这一概念。
例子
- 如果路径包含每一对顶点,那么图就是连通的。
- 如果一个有向图中存在包含每对顶点的相对有向路径,那么这就是强连接有向图 Strongly-connected digraph。
- 没有边连接两个不连续的路径顶点的路径称为诱导路径 induced path。
- 包含图的每个顶点的路径称为哈密顿路径 Hamiltonian Path。
- 如果两条路径没有任何共同的内部顶点,那么它们与顶点无关(换言之,内部顶点不相交)。类似地,如果两条路径没有任何共同的内边,那么它们是边独立的(或边不相交)。两条内部顶点不相交的路径的边也不相交,但反之未必正确的。
- 图中两个顶点之间,如果最短路径存在,那么它们的的距离是最短路径的长度,否则该距离是无穷大。
- 连接图的直径是图的顶点对之间的最大距离(如上定义)。
路径寻找
求解图的最短和最长路径有多种算法,但是前者的计算比后者简单得多。
Dijkstra 算法产生了一个从源顶点到无向或有向图中每个顶点的最短路径列表,而Bellman-Ford 算法 可以应用于具有负边权重的有向图。利用 Floyd-Warshall 算法可以求出加权有向图中所有顶点对之间的最短路径。
参见
- 图论词汇 Glossary of graph theory
- 路径图 Path graph
- 多边形链 Polygonal chain
- 最短路径问题 Shortest path problem
- 最长路径问题 Longest path problem
- Dijkstra算法 Dijkstra's algorithm
- Bellman–Ford算法 Bellman–Ford algorithm
- Floyd–Warshall算法 Floyd–Warshall algorithm
- 自我避免的步道 Self-avoiding walk
- 最短路径图Shortest-path graph
参考文献
其他链接
- Bender, Edward A.; Williamson, S. Gill (2010). Lists, Decisions and Graphs. With an Introduction to Probability. https://books.google.fr/books?id=vaXv_yhefG8C.
- Bondy, J. A.; Murty, U. S. R. (1976). Graph Theory with Applications. North Holland. p. 12-21. ISBN 0-444-19451-7. https://archive.org/details/graphtheorywitha0000bond/page/12.
- Diestel, Reinhard (2005). Graph Theory. Springer-Verlag. p. 6-9. ISBN 3-540-26182-6. http://www.math.uni-hamburg.de/home/diestel/books/graph.theory/.
- Gibbons, A. (1985). Algorithmic Graph Theory. Cambridge University Press. p. 5-6.
- Korte, Bernhard; Lovász, László; Prömel, Hans Jürgen; Schrijver, Alexander (1990). Paths, Flows, and VLSI-Layout. Springer-Verlag. https://archive.org/details/pathsflowsvlsila0000unse.
本中文词条由Ryan翻译,CecileLi审校,薄荷编辑,欢迎在讨论页面留言。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。