演化网络

此词条暂由彩云小译翻译，已由Steve Luo审校。

基于初始巴拉巴西-阿尔伯特 Barabasi-Albert 模型的演化网络的动画

演化网络 Evolving networks是作为时间的函数而变化的网络。它们是网络科学 network science的自然延伸，因为几乎所有现实世界的网络都是随时间演化的，通过随着时间的推移增加或删除节点或连边实现。通常所有这些过程都是同时发生的，比如在社交网络 social networks中，随着时间的推移人们结交和失去朋友，从而创造和破坏连边，一些人成为新的社交网络的一部分，或者离开他们的网络，从而改变网络中的节点。演化网络的概念建立在既定的网络理论之上，现在正被引入到许多不同领域的网络研究中。

网络理论背景

网络研究源于图论 graph theory的发展，莱昂哈德·欧拉 Leonhard Euler于1736年首先分析了图论，当时他撰写了著名的柯尼斯堡七桥问题 Seven Bridges of Königsberg论文。随后在八篇由保罗·埃尔德什 Paul Erdős和阿尔弗雷德·雷尼 Alfréd Rényi撰写的研究随机图 random graphs的著名论文的帮助下，概率网络理论得以发展。埃尔德什-雷尼模型 Erdős–Rényi model(ER模型)假定一个图由n个有标记的节点组成，其中每一对节点通过一个预设的概率p连接。

Watts–Strogatz graph 瓦茨-斯托加茨图

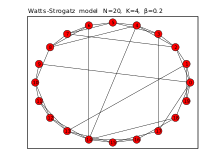
尽管ER模型的简单性帮助它找到了许多应用之处，但它并不能准确地描述许多真实世界的网络。ER模型无法像在现实世界网络中那样频繁地生成局部聚类和三元闭包。为此，提出了瓦茨-斯托加茨模型 Watts-Strogatz model，将网络构造成规则的环网格，然后根据一定的概率β重新连接节点。

这会产生一个局部聚集的网络，并显著减少平均路径长度 average path length。这样创建的网络可以代表在许多现实世界网络中观察到的小世界现象 small world phenomenon。

尽管取得了这样的成就，ER模型和Watts-Storgatz模型都未能解释在许多现实世界网络中观察到的中心节点的形成。ER模型中的度分布遵循泊松分布，而Watts-Strogatz模型生成的图在度上是同质的。但是，许多网络是无标度的，这意味着它们的度分布遵循以下形式的幂律分布:

[math]\displaystyle{ P(k)\sim k^{-\gamma} }[/math]

对于许多现实世界的网络来说，这个指数大约是3。然而，它不是一个通用常数，并且持续地依赖于网络的参数。

第一个演化网络模型——无标度网络

巴拉巴西-阿尔伯特模型 Barabási–Albert model(BA模型)是第一个被广泛接受的产生无标度网络 scale-free network的模型。这是通过偏好依附 preferential attachment和增长来实现的，随着时间的推移，节点被添加到网络中，并且更有可能链接到其他度较大的节点。BA模型首先应用于互联网的度分布，这两种影响都可以清楚地看到。随着时间的推移，新的网页会不断增加，并且每个新的网页都更有可能链接到像谷歌这样具有很高的度分布的高度可见的中心节点，而不是只有少量链接的节点。从形式上来说，这种偏好依附是:

[math]\displaystyle{ p_i = \frac{k_i}{\displaystyle\sum_j k_j}, }[/math]

BA模型以外

BA模型是第一个从随着时间的推移而添加节点和连边的网络构造方式中推导出网络拓扑的模型。然而，该模型只做了产生无标度网络所必需的最简单的假设，即存在线性增长和线性偏好依附。这个最小模型没有刻画度分布形状的变化，度指数的变化，或不依赖大小的集聚系数 clustering coefficient。

因此，通过引入一些新的性质，对原有的模型进行了修改，以更充分地刻画演化网络的性质。

适应度

与BA模型有关的一个问题是，每个节点的度分布经历很强的正反馈 positive feedback，即最早的具有高度分布的节点继续无限期地主宰网络。但是，可以通过为每个节点引入一个适应度来缓解这个问题，该适应度可以修改用该节点创建新链接的概率，甚至可以修改该节点的链接被删除的概率。

为了保持BA模型中的偏好依附，该适应度乘以基于度分布的偏好依附，得到连接到节点i的真实概率。

[math]\displaystyle{ \Pi(k_i) = \frac{\eta_i k_i}{\displaystyle\sum_j \eta_j k_j}, }[/math]

其中[math]\displaystyle{ \eta }[/math]是适应度，这也可能依赖于时间。适应度可能随时间衰减，可以表示为

[math]\displaystyle{ \Pi(k_i) \propto k_i(t-t_i)^{-\nu}, }[/math]

其中[math]\displaystyle{ \gamma }[/math]随[math]\displaystyle{ \nu. }[/math]的增长而增长。

删除节点和重连接边

由于节点可能会以一定的概率从网络中移除，因此会出现更多的复杂情况。此外，节点之间现有的链接可能会被删除并且创建新的链接。这些行为发生的概率可能依赖于时间，也可能与节点的适应度有关。通过研究有关网络的特性，可以为这些事件赋予概率，从而生成具有相同特性的模型网络。这种增长将在每个时间步骤中发生下列行为之一:

概率 p：增加一个内部链接。

概率 q: 删除一个链接。

概率 r：删除一个节点。

概率 1-p-q-r: 添加一个节点。

描述演化网络的其他方法

除了上面描述的不断生长的网络模型之外，可能有时候其他方法对于描述演化网络的某些性质更有用或更方便。

趋向均衡

在竞争性决策发生的网络系统中，博弈论经常被用来建模系统动力学，趋向均衡可以被认为是拓扑进化的驱动力。例如Kasthurirathna和Piraveenan表明，当一个系统中的个体表现出不同程度的理性时，提高整个系统的理性可能是无标度网络出现的进化原因。他们通过对一个最初的随机网络施加进化压力来模拟一系列经典博弈，当允许重新连接时，网络收敛到纳什均衡，从而证明了这一点。在这个过程中，网络变得越来越无标度。

视演化网络为连续的静态网络快照

观察不断演化的网络最常用的方法是把它们看作连续的静态网络。这可以概念化为组成电影的一个个静态图像。有许多简单的参数可以描述一个静态网络（节点数、边、路径长度、连通子图），或者描述图中的特定节点，比如链接数或集聚系数。然后可以使用信号处理概念将这些属性单独作为时间序列进行研究。 例如，我们可以通过查看网络的连续快照并计算每个快照中的链接数量，来跟踪每分钟建立到服务器的链接数量。

不幸的是，快照与电影的类比也揭示了这种方法的主要困难: 使用的时间步骤很少由网络给出，而是任意的。在每个快照之间使用极小的时间步骤可以保持分辨率，但实际上可能掩盖了只有在较长时间尺度下才能看到的更广泛的趋势。相反，使用较大的时间尺度会失去每个快照中事件的时间顺序。因此，可能很难找到合适的时间尺度来将网络的演化划分为静态快照。

定义动力学性质

那些不能直接从将演化网络视为一系列快照中观察到的特性可能很重要，例如节点之间的接触时间。可以定义其他类似的属性，然后可以通过网络的演化来跟踪这些属性，并直接可视化它们。

使用连续快照的另一个问题是，在网络拓扑中微小的变化可以对用于寻找网络社团的算法的结果产生巨大的影响。因此，有必要使用一个非经典的社团定义，它允许通过一系列的规则，如出生、死亡、合并、分裂、生长和收缩，来跟随社团的演化。

应用

2009年世界预定商业航空交通路线图。这个网络随着新路线的计划或取消而不断演变

几乎所有真实世界的网络都是不断演化的网络，因为它们是随着时间的推移而构建的。通过改变上述各自的概率，可以使用扩展的BA模型来构造一个具有与许多观测网络几乎相同属性的网络。

此外，无标度网络的概念告诉我们，时间演化是理解网络属性的必要组成部分，而且很难将现有网络模型化为瞬间创建的。目前正在研究的演化网络包括社交网络、通信网络、互联网、电影演员网络、万维网和交通网络。

扩展阅读

• "Understanding Network Science," https://web.archive.org/web/20110718151116/http://www.zangani.com/blog/2007-1030-networkingscience

• "Linked: The New Science of Networks", A.-L. Barabási Perseus Publishing, Cambridge.

References

---

本中文词条由Steve Luo审校，打豆豆，欢迎在讨论页面留言。

本词条内容源自wikipedia及公开资料，遵守 CC3.0协议。