帕累托最优

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
薄荷（讨论 | 贡献）2020年12月20日 (日) 18:57的版本
跳到导航 跳到搜索

帕累托效率 Pareto efficiency 或帕累托最优 Pareto optimality是一种不能再改进的状态，它使得任何个体或偏好准则变得更好而不使任意一个个体或一项偏好准则变得更差。这个概念是以意大利工程师、经济学家维尔弗雷多·帕累托 Vilfredo Pareto（1848-1923）的名字命名的。他在研究经济效率 economic efficiency和收入分配 income distribution时使用了这个概念。以下三个概念密切相关：

  • 在一个给定的初始条件下，帕累托改进 Pareto improvement 指的是一种大多数主体的弱偏好选择，被至少一个主体严格优选的状态。在某种意义上，它是一种一致同意的改进：如果我们处于这种新的情况下，一些主体会获利，且没有主体会蒙受损失。
  • 一种状态如果存在帕累托改进，那么它被称作受帕累托支配 Pareto dominated 的。
  • 一种状态如果是不受帕累托支配的，那么它被称作帕累托最优的或帕累托有效的。

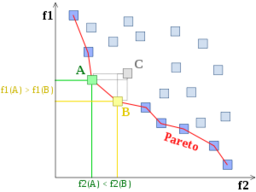
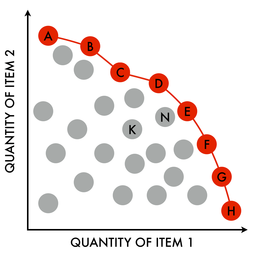
帕累托边界 Pareto frontier 是所有帕累托有效分配的集合，按惯例以图表形式表示它。它也被称为帕累托前沿 Pareto front 或帕累托集 Pareto set 。[1]

“帕累托最优”被认为是一种狭义的效率，它不一定会产生社会所期望的资源分配: 它没有为平等或一个社会的总体福祉发声。[2][3]它是效率的必要不充分条件。

除了分配效率的背景之外，帕累托最优的概念也出现在生产效率 efficiency in production对比于x-低效率 x-inefficiency的背景之下，即如果生产投入没有可行的再分配，使得一种产品的产出增加，而所有其他产品的产出增加或保持不变，那么这一组产品的产出就是帕累托最优的。[4]

除了经济学，帕累托最优的概念已经应用到工程和生物学中的替代品的选择。首先根据多项标准对每个选项进行评估，然后确定选项子集，没有其他选项的属性可以绝对胜过选定的选项。在多目标优化 multi-objective optimization(又称帕累托优化)中，这是不可能在不损害其他变量的情况下改进一个变量的陈述。

综述

“帕累托最优”是一个正式定义的概念，用来描述一个分配何时是最优的。如果有一种替代性的分配方式可以在不降低任何其他参与者福祉的情况下改善至少一个参与者的福祉，那么这种分配就不是帕累托最优的。如果有一个转移满足这个条件，这个再分配就被称为“帕累托改进”。当无法进一步实现帕累托改进时，这个分配就是“帕累托最优”。

这个概念在经济体系中的正式表述如下: 考虑一个经济体系有[math]\displaystyle{ n }[/math]个主体和[math]\displaystyle{ k }[/math]个商品，如果没有其他可行的分配[math]\displaystyle{ \{x_1, ..., x_n\} }[/math]使得效用函数[math]\displaystyle{ u_i }[/math]对任意主体[math]\displaystyle{ i }[/math]满足[math]\displaystyle{ x_i \in \mathbb{R}^k }[/math]，对某些主体[math]\displaystyle{ i }[/math]满足[math]\displaystyle{ u_i(x_i') \gt u_i(x_i) }[/math]，那么这个分配[math]\displaystyle{ \{x_1', ..., x_n'\} }[/math]是帕累托最优的，其中对任意[math]\displaystyle{ i }[/math]，[math]\displaystyle{ x_i \in \mathbb{R}^k }[/math]此处需插入公式。[5]在这个简单的经济体系中，“可行性”是指一种分配，其中每种商品的分配总额不超过该经济体系中所有商品的总额。在一个生产能力更为复杂的经济体中，一种分配将包括消费载体和生产载体，且可行性要求每种消费品的总量不大于初始禀赋加上生产总量。

原则上，从一个普遍低效率的经济分配到一个高效率的经济分配的转变不一定被认为是帕累托改进。即使经济总体是获益的，如果一个主体在再分配中处于不利地位，这个分配也不是帕累托最优的。例如，如果经济政策的某个改变消除了垄断，市场随后变得具有竞争力，那么其他主体的收益可能很大。然而，由于垄断者处于不利地位，这不是帕累托改进。理论上，如果经济体系的收益大于垄断者的损失，考虑到帕累托改进，垄断者可以在为经济体系中的其他主体留下净收益的情况下得到补偿。因此，在实践中，为了确保没有人会因为旨在实现帕累托最优的改变而处于不利地位，可能需要对一个或多个当事方进行补偿。在现实世界中，人们公认，这种补偿可能会造成意外的后果，随着时间的推移动机扭曲，因为代理人可能预期这种补偿并相应地改变他们的行为。

在福利经济学第一定理 the first welfare theorem的理想条件下，一个自由市场 free market系统，也称为“竞争均衡 competitive equilibrium” ，对应一个帕累托有效的结果。经济学家肯尼斯·阿罗 Kenneth Arrow和杰拉德·迪布鲁 Gérard Debreu首先用数学方法证明了这一点。

然而，这个结果只有在证明所需的限制性假设下才成立，即所有可能的商品都存在市场，因此不存在外部效应; 所有市场都处于完全均衡状态; 市场是完全竞争的; 交易成本是可忽略的; 市场参与者拥有完全信息 perfect information。

根据格林沃德-斯蒂格利茨定理 the Greenwald-Stiglitz theorem，在缺乏完全信息或完全市场的情况下，这个结果通常是帕累托低效的。[6]

福利经济学第二定理 The second welfare theorem实质上是福利经济学第一定理的逆定理。它指出，在类似的理想假设下，任何帕累托最优都可以通过某种竞争均衡或自由市场制度获得，尽管它可能也需要一次性转移财富。[5]

弱帕累托效率

弱帕累托最优 Weak Pareto optimality 是一种不能严格地改善每个个体的状态。[7]

在形式上，我们将强帕累托改进 strong pareto improvement 定义为所有主体严格处于较好状态的情况（与之相对的是“帕累托改进” ，它要求一个主体严格处于较好状态，而其他主体至少同样良好)。没有强帕累托改进的状态是弱帕累托最优的。

任何强帕累托改进也是弱帕累托改进。反之则不然; 例如，考虑一个包含两种资源的资源分配问题，Alice资源为10,0，George资源为5,5。考虑将所有资源分配给 Alice，它的'分配方案为（10，0）。

  • 它是一个弱帕累托最优，因为没有其他任何分配对上述两个主体是更优的（没有强帕累托改进）。
  • 但它不是一个强帕累托最优，因为George得到的第二种的资源的分配对George是严格更优的且对Alice是弱更优的（它是一个弱帕累托改进），它的分配方案为（10，5）

市场不需要局部不饱和 local nonsatiation 就能达到弱帕累托最优。[8]

受约束的帕累托效率

受约束的帕累托最优 Constrained Pareto optimality 是帕累托最优的弱化，因为一个潜在的规划者（比如政府）可能无法改进分散市场的结果，即使这个结果是低效的。如果它受到与独立主体相同的信息或机构约束的限制，就会发生这种情况。[9]

例如，个人拥有私人信息的情况（例如，劳动力市场中工人自己的生产率为工人所知，而潜在雇主却不知道，或者二手车市场中汽车的质量为卖方所知，而非买方所知)导致道德风险或不利选择和次优结果。在这种情况下，希望改善局面的规划者不太可能获得市场参与者没有的信息。因此，计划者不能执行基于个人特质的分配规则； 例如，”如果一个人属于 a 型，他们支付 p1的价格，但如果属于 b 型，他们支付 p2的价格”（见林达尔价格 Lindahl prices ）。基本上，只有隐性规则（类似于“每个人都支付价格 p”）或基于可观察行为的规则被允许； “如果任何人以价格 px 选择 x，那么他们将得到10美元的补贴，除此之外什么也得不到”。如果不存在能够成功改进市场结果的允许规则，那么该结果被称为是“受约束的帕累托最优的”。

受约束的帕累托最优的概念假定了规划者是仁慈的，因此不同于政府失灵 government failure 的概念。政府失灵在制定政策的政客未能取得最佳结果时会出现，仅仅因为他们的行为不一定符合公众的最大利益。

部分帕累托效率

部分帕累托最优 Fractional Pareto optimality 是在物品公平分配的背景下对帕累托最优的一个加强。如果一个不可分割的物品的分配不是受帕累托支配的，即使在分配过程中，一些物品在主体之间被分配，那么它是部分帕累托最优 fractionally Pareto-optimal（fPO） 。这与标准的帕累托最优相反，因为它只考虑可行（离散）分配的控制。[10]

作为一个示例，考虑一个有两种物品的分配问题，Alice 值为3,2，George 值为4,1。考虑将第一种物品分配给 Alice，第二种物品分配给 George，其中分配方案为（3，1）。

  • 它是一个帕累托最优，因为其他任何离散分配（在不分离物品的情况下）都会使得某个主体变差。
  • 但是，它不是部分帕累托最优的，因为它是受帕累托支配的。它分配给了Alice第一种物品的一半和第二种物品的全部，分配给了George第一种物品的一半。它的分配方案是（3.5，2）。

帕累托效率和福利最大化

假设每个主体 i 被赋予一个正权重。对于每个分配 x ，将 x 的福利定义为 x 中所有主体的配置的加权和，即:[math]\displaystyle{ W_a(x) := \sum_{i=1}^n a_i u_i(x) }[/math].

假设[math]\displaystyle{ x\lt sub\gt a\lt /sub\gt }[/math]此处需插入公式是一个在所有分配中使福利最大化的分配，即:[math]\displaystyle{ x_a \in \arg \max_{x} W_a(x) }[/math].

很容易证明分配[math]\displaystyle{ x\lt sub\gt a\lt /sub\gt }[/math]是帕累托有效的: 因为所有[math]\displaystyle{ x\lt sub\gt a\lt /sub\gt }[/math]的权重都是正的，任何帕累托改进都会增加加权和，这与[math]\displaystyle{ x\lt sub\gt a\lt /sub\gt }[/math]'的定义相矛盾。

日本新瓦尔拉斯经济学家根岸隆史 Takashi Negishi证明，[11]在某些假设下，该命题的逆命题也成立，即对于每一个帕累托有效的配置x，都存在一个正向量a，使最大化。哈尔·瓦里安提供了一个较短的证明。[12]

工程学上的应用

帕累托最优的概念已经在工程中得到了应用。[13]给定一组选择和一种评估它们的方法，帕累托边界、帕累托解集或帕累托前沿就是帕累托有效的选择集。通过将注意力限制在帕累托有效的选择集上，设计者可以在这个集合中进行权衡，而不是考虑每个参数的全部范围。[14]

帕累托边界的一个例子。集合中的点表示可行的选择，较小的值比较大的值更好。点C不在帕累托边界上，因为它同时被点 A 和点 B 支配。点A和点B不受任何其他点严格控制，因此位于边界上。
一个生产可能性边界 production-possibility frontier。红线是帕累托有效边界的一个例子，边界和左下方的区域是一个连续的选择集。边界上的红点是生产的帕累托最优选择的例子。边界外的点，如 N 和K，不是帕累托有效，因为在边界上存在着受帕累托支配的点。

帕累托边界

对于一个给定的系统，帕累托边界the Pareto frontier或帕累托集是所有帕累托有效的参数化（分配）的集合。找到帕累托前沿在工程学中特别有用。通过产生所有潜在的最优解决方案，设计师可以在这个受限的参数集中进行集中的权衡，而不需要考虑所有的参数。[15]

帕累托边界, P（Y） ，可以更正式地描述如下。考虑一个包含函数 [math]\displaystyle{ f: \mathbb{R}^n \rightarrow \mathbb{R}^m }[/math]的系统，其中X是度量空间 metric space [math]\displaystyle{ \mathbb{R}^n }[/math]中可行决策的紧集 compact set，Y是[math]\displaystyle{ \mathbb{R}^m }[/math]中标准向量的可行集，使得[math]\displaystyle{ Y = \{ y \in \mathbb{R}^m:\; y = f(x), x \in X\;\} }[/math]。

我们假设标准值的最优方向是已知的。[math]\displaystyle{ y^{\prime\prime} \in \mathbb{R}^m }[/math]中的一个点优于中的另一个点[math]\displaystyle{ y^{\prime} \in \mathbb{R}^m }[/math]，写作[math]\displaystyle{ y^{\prime\prime} \succ y^{\prime} }[/math]。因此，帕累托边界可以被描述为:

[math]\displaystyle{ P(Y) = \{ y^\prime \in Y: \; \{y^{\prime\prime} \in Y:\; y^{\prime\prime} \succ y^{\prime}, y^\prime \neq y^{\prime\prime} \; \} = \empty \}. }[/math]

边际替代率

经济学中，帕累托边界的一个重要方面是在帕累托有效分配中，所有消费者的边际替代率 the marginal rate of substitution是相同的。一个正式的陈述可以通过考虑一个有m个消费者和n个商品的系统，以及每个消费者的效用函数[math]\displaystyle{ z_i=f^i(x^i) }[/math]来推导出。在这个效用方程中，对所有的i，[math]\displaystyle{ x^i=(x_1^i, x_2^i, \ldots, x_n^i) }[/math]是商品的矢量。可行性约束为[math]\displaystyle{ \sum_{i=1}^m x_j^i = b_j }[/math]。为了找到帕累托最优分配，我们最大化拉格朗日函数 Lagrangian:

[math]\displaystyle{ L_i((x_j^k)_{k,j}, (\lambda_k)_k, (\mu_j)_j)=f^i(x^i)+\sum_{k=2}^m \lambda_k(z_k- f^k(x^k))+\sum_{j=1}^n \mu_j \left( b_j-\sum_{k=1}^m x_j^k \right) }[/math]

其中[math]\displaystyle{ (\lambda_k)_k }[/math]和[math]\displaystyle{ (\mu_j)_j }[/math]是乘子的向量。取关于商品的拉格朗日函数的偏导数[math]\displaystyle{ x_j^k }[/math]（[math]\displaystyle{ j=1,\ldots,n }[/math] ，[math]\displaystyle{ k=1,\ldots, m }[/math]）并给出以下一阶条件系统:

对于[math]\displaystyle{ j=1,\ldots,n }[/math]：

[math]\displaystyle{ \frac{\partial L_i}{\partial x_j^i} = f_{x^i_j}^1-\mu_j=0\ }[/math]

对于[math]\displaystyle{ k= 2,\ldots,m }[/math] ， [math]\displaystyle{ j=1,\ldots,n }[/math]：

[math]\displaystyle{ \frac{\partial L_i}{\partial x_j^k} = -\lambda_k f_{x^k_j}^i-\mu_j=0 }[/math]

其中[math]\displaystyle{ f_{x^i_j} }[/math]表示[math]\displaystyle{ f }[/math]对于[math]\displaystyle{ x_j^i }[/math]的偏导数。现给定[math]\displaystyle{ k\neq i }[/math]且[math]\displaystyle{ j,s\in \{1,\ldots,n\} }[/math]。上述一阶条件意味着

[math]\displaystyle{ \frac{f_{x_j^i}^i}{f_{x_s^i}^i}=\frac{\mu_j}{\mu_s}=\frac{f_{x_j^k}^k}{f_{x_s^k}^k}. }[/math]

因此，在帕累托最优分配中，所有消费者的边际替代率必须相同。[16]

计算

计算机科学和动力工程给出了计算有限个方案集的帕累托边界的算法。[17]它们包括:

  • “标量化算法”，或称加权求和法。[21][22]

在生物学中的应用

帕累托最优化在生物过程中也有研究。[25]在细菌中，基因要么生成成本低廉（资源节约型） ，要么更容易被读取（翻译效率型）。自然选择将高表达的基因推向资源利用和翻译效率的帕累托边界。帕累托边界附近基因的进化速度也较慢（这表明它们提供了一种选择优势）。[26]

批判

把帕累托最优等同于社会优化是不正确的，[27]因为后者是一个规范性概念，是一个典型的解释性问题，可以解释分配不平等程度的后果。[28]一个例子就是对一个财产税收入较低的学区和另一个财政收入高很多的学区的解释，这表明在政府再分配的帮助下实现了更加平等的分配。[29]

帕累托效率并不需要完全公平的财富分配。[30]一个少数富人拥有绝大多数资源的经济体系可以是帕累托有效的。这种可能性是帕累托效率的固有定义; 通常情况下，无论财富的公平分配程度如何，现状都是帕累托有效的。一个简单的例子是在三个人之间分配馅饼。最公平的分配将分配给每个人三分之一。

另一种分配是两个人各占半部分，第三个人不占分毫。然而，尽管这种分配并不公平，它也是帕累托最优的，因为没有一个接受者能够在不减少其他人的份额的情况下得到更优的收益; 还有其他许多这样的分配例子。帕累托无效率的馅饼分配的一个例子是三者中的每一个分得馅饼的四分之一，剩下的部分丢弃。[31]在这些示例中，馅饼的缘由（和实用价值）被认为是无关紧要的。在这种情况下，由于潜在的分配者都没有实际生产，却获得了“意外之财”（例如，土地、继承的财产、广播频谱的一部分或其他资源） ，帕累托最优的标准并不能决定唯一的最优分配。由于市场准入门槛等原因，财产整合可能会将他者排除在财产积累之外。

阿马蒂亚·森 Amartya Sen阐述的自由主义悖论 The liberal paradox表明，当人们对他人的行为有偏好时，帕累托有效的目标可能与个人自由的目标发生冲突。[32]

请参阅

参考资料

  1. ↑ proximedia. "Pareto Front". www.cenaero.be. Retrieved 2018-10-08.
  2. ↑ Sen, A. (October 1993). "Markets and freedom: Achievements and limitations of the market mechanism in promoting individual freedoms" (PDF). Oxford Economic Papers. 45 (4): 519–541. doi:10.1093/oxfordjournals.oep.a042106.
  3. ↑ Barr, N. (2012). "3.2.2 The relevance of efficiency to different theories of society". Economics of the Welfare State (5th ed.). Oxford University Press. pp. 46–49. 
  4. ↑ John D. Black, Hashimzade, N., & Gareth Myles, eds., A Dictionary of Economics, 5th ed. (Oxford: Oxford University Press, 2017)， p. 459.
  5. ↑ 5.0 5.1 Mas-Colell, A.; Whinston, Michael D.; Green, Jerry R. (1995), "Chapter 16: Equilibrium and its Basic Welfare Properties", Microeconomic Theory, Oxford University Press, ISBN 978-0-19-510268-0
  6. ↑ Greenwald, B.; Stiglitz, J. E. (1986). "Externalities in economies with imperfect information and incomplete markets". Quarterly Journal of Economics. 101 (2): 229–64. doi:10.2307/1891114.
  7. ↑ Mock, William B T. (2011). "Pareto Optimality". Encyclopedia of Global Justice. pp. 808–809. doi:10.1007/978-1-4020-9160-5_341. ISBN 978-1-4020-9159-9. 
  8. ↑ Markey‐Towler, Brendan and John Foster. "Why economic theory has little to say about the causes and effects of inequality", School of Economics, University of Queensland, Australia, 21 February 2013, RePEc:qld:uq2004:476
  9. ↑ Magill, M., & Martine Quinzii, Theory of Incomplete Markets, MIT Press, 2002, p. 104.
  10. ↑ Barman, S., Krishnamurthy, S. K., & Vaish, R., "Finding Fair and Efficient Allocations", EC '18: Proceedings of the 2018 ACM Conference on Economics and Computation, June 2018.
  11. ↑ Negishi, Takashi (1960). "Welfare Economics and Existence of an Equilibrium for a Competitive Economy". Metroeconomica. 12 (2–3): 92–97. doi:10.1111/j.1467-999X.1960.tb00275.x.
  12. ↑ Varian, Hal R. (1976). "Two problems in the theory of fairness". Journal of Public Economics. 5 (3–4): 249–260. doi:10.1016/0047-2727(76)90018-9. hdl:1721.1/64180.
  13. ↑ Goodarzi, E., Ziaei, M., & Hosseinipour, E. Z., Introduction to Optimization Analysis in Hydrosystem Engineering (Berlin/Heidelberg: Springer, 2014), pp. 111–148.
  14. ↑ Jahan, A., Edwards, K. L., & Bahraminasab, M., Multi-criteria Decision Analysis, 2nd ed. (Amsterdam: Elsevier, 2013), pp. 63–65.
  15. ↑ Costa, N. R., & Lourenço, J. A., "Exploring Pareto Frontiers in the Response Surface Methodology", in G.-C. Yang, S.-I. Ao, & L. Gelman, eds., Transactions on Engineering Technologies: World Congress on Engineering 2014 (Berlin/Heidelberg: Springer, 2015), pp. 399–412.
  16. ↑ Wilkerson, T., Advanced Economic Theory (Waltham Abbey: Edtech Press, 2018), p. 114.
  17. ↑ Tomoiagă, Bogdan; Chindriş, Mircea; Sumper, Andreas; Sudria-Andreu, Antoni; Villafafila-Robles, Roberto (2013). "Pareto Optimal Reconfiguration of Power Distribution Systems Using a Genetic Algorithm Based on NSGA-II". Energies. 6 (3): 1439–55. doi:10.3390/en6031439.
  18. ↑ Nielsen, Frank (1996). "Output-sensitive peeling of convex and maximal layers". Information Processing Letters. 59 (5): 255–9. CiteSeerX 10.1.1.259.1042. doi:10.1016/0020-0190(96)00116-0.
  19. ↑ Kung, H. T.; Luccio, F.; Preparata, F.P. (1975). "On finding the maxima of a set of vectors". Journal of the ACM. 22 (4): 469–76. doi:10.1145/321906.321910.
  20. ↑ Godfrey, P.; Shipley, R.; Gryz, J. (2006). "Algorithms and Analyses for Maximal Vector Computation". VLDB Journal. 16: 5–28. CiteSeerX 10.1.1.73.6344. doi:10.1007/s00778-006-0029-7.
  21. ↑ Kim, I. Y.; de Weck, O. L. (2005). "Adaptive weighted sum method for multiobjective optimization: a new method for Pareto front generation". Structural and Multidisciplinary Optimization. 31 (2): 105–116. doi:10.1007/s00158-005-0557-6. ISSN 1615-147X.
  22. ↑ Marler, R. Timothy; Arora, Jasbir S. (2009). "The weighted sum method for multi-objective optimization: new insights". Structural and Multidisciplinary Optimization. 41 (6): 853–862. doi:10.1007/s00158-009-0460-7. ISSN 1615-147X.
  23. ↑ "On a Bicriterion Formulation of the Problems of Integrated System Identification and System Optimization". IEEE Transactions on Systems, Man, and Cybernetics. SMC-1 (3): 296–297. 1971. doi:10.1109/TSMC.1971.4308298. ISSN 0018-9472.
  24. ↑ Mavrotas, George (2009). "Effective implementation of the ε-constraint method in Multi-Objective Mathematical Programming problems". Applied Mathematics and Computation. 213 (2): 455–465. doi:10.1016/j.amc.2009.03.037. ISSN 0096-3003.
  25. ↑ Moore, J. H., Hill, D. P., Sulovari, A., & Kidd, L. C., "Genetic Analysis of Prostate Cancer Using Computational Evolution, Pareto-Optimization and Post-processing", in R. Riolo, E. Vladislavleva, M. D. Ritchie, & J. H. Moore, eds., Genetic Programming Theory and Practice X (Berlin/Heidelberg: Springer, 2013), pp. 87–102.
  26. ↑ Seward, Emily A.; Kelly, Steven (2018). "Selection-driven cost-efficiency optimization of transcripts modulates gene evolutionary rate in bacteria". Genome Biology. 19 (1): 102. doi:10.1186/s13059-018-1480-7. PMC 6066932. PMID 30064467.
  27. ↑ Jacques Drèze, Essays on Economic Decisions Under Uncertainty (Cambridge: Cambridge University Pres], 1987), pp. 358–364
  28. ↑ Backhaus, J. G., The Elgar Companion to Law and Economics （Cheltenham/ Northampton, MA: Edward Elgar Publishing, 2005), pp. 10–15.
  29. ↑ Paulsen, M. B., "The Economics of the Public Sector: The Nature and Role of Public Policy in the Finance of Higher Education", in M. B. Paulsen, J. C. Smart, eds. The Finance of Higher Education: Theory, Research, Policy, and Practice (New York: Agathon Press, 2001), pp. 95–132.
  30. ↑ Bhushi, K., ed., Farm to Fingers: The Culture and Politics of Food in Contemporary India (Cambridge: Cambridge University Press, 2018), p. 222.
  31. ↑ Wittman, D., Economic Foundations of Law and Organization (Cambridge: Cambridge University Press, 2006), p. 18.
  32. ↑ Sen, A., Rationality and Freedom ([Cambridge, Massachusetts / London: Harvard University Press, 2004), pp. 92–94.

延伸阅读

  • Bendor, Jonathan; Mookherjee, Dilip (April 2008). "Communitarian versus Universalistic norms". Quarterly Journal of Political Science. 3 (1): 33–61. doi:10.1561/100.00007028. {{cite journal}}: Invalid |ref=harv (help)
  • Rubinstein, Ariel; Osborne, Martin J. (1994), "Introduction", in Rubinstein, Ariel; Osborne, Martin J. (eds.), A course in game theory, Cambridge, Massachusetts: MIT Press, pp. 6–7, ISBN 9780262650403 Book preview.
  • Mathur, Vijay K. (Spring 1991). "How well do we know Pareto optimality?". The Journal of Economic Education. 22 (2): 172–178. doi:10.2307/1182422. {{cite journal}}: Invalid |ref=harv (help)
  • Newbery, David M.G.; Stiglitz, Joseph E. (January 1984). "Pareto inferior trade". Review of Economic Studies. 51 (1): 1–12. doi:10.2307/2297701. {{cite journal}}: Invalid |ref=harv (help)


本中文词条由袁一博翻译，由Flipped完成审校，打豆豆编辑，欢迎在讨论页面留言。

本词条内容源自wikipedia及公开资料，遵守 CC3.0协议。

取自“https://wiki.swarma.org/index.php?title=帕累托最优&oldid=20260”