顶点
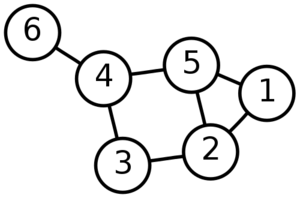
在数学上,更具体地说在图论中,图这一抽象对象的基本组成单元是顶点或节点:无向图由一组顶点和一组边(每条边由一对顶点组成,不区分这俩顶点的顺序)组成,而有向图由一组顶点和一组弧(每条弧由一对顶点组成,区分这俩顶点的顺序)组成。在抽象图的图示中,一般而言,带标注的圆圈表示顶点,两个顶点之间的直线或箭头表示边。直线用于表示无向图的边,箭头表示有向图的边。
从图论的观点来看,顶点被视为没有属性且不可分割的对象。无论这些顶点所组成的图来自什么样的应用场景,无论在这些应用场景中,顶点所表示的对象又有什么额外的结构。例如: 计算机科学领域中的语义网络,就可以抽象为图,其顶点表示概念或对象的类。
若图包含由顶点[math]\displaystyle{ v }[/math]和[math]\displaystyle{ w }[/math]组成的边[math]\displaystyle{ (v,w) }[/math],则称顶点[math]\displaystyle{ w }[/math]邻接于adjacent to顶点[math]\displaystyle{ v }[/math];由所有邻接于[math]\displaystyle{ v }[/math]的顶点而组成 的图,被称为这些顶点的导出子图induced subgraph,它也被称为顶点[math]\displaystyle{ v }[/math]的邻域 neighborhood。
顶点类型
在抽象图中,顶点[math]\displaystyle{ v }[/math]的度 degree,记作[math]\displaystyle{ 𝛿(v) }[/math],是所有关联于[math]\displaystyle{ v }[/math]的边的数量。度为0的顶点被称作孤立顶点 isolated vertex,这样的顶点不是任何边的端点(如图2所示,这一抽象图中含有一个孤立顶点)[1]
度为1的顶点被称为叶顶点 leaf vertex,也称叶子顶点、叶节点、悬挂顶点 pendant vertex。
在有向图中,我们可以根据边的方向,把顶点的度分为出度 outdegree(也称出次数),记作[math]\displaystyle{ 𝛿^+(v) }[/math]和入度 indegree(也称入次数),记作[math]\displaystyle{ 𝛿^−(v) }[/math]。一个顶点的出度指的是,所有从这个顶点出发,连接其他顶点的箭头的数量。与此相反,一个顶点的入度指的是,所有从其他顶点出发,连接到这个顶点的箭头的数量。在有向图中,有可能出现两种顶点:源顶点 source vertex 和汇顶点 sink vertex。前者指入度为0的顶点,后者指出度为0的顶点。
若一个顶点的邻域恰好能构成团 clique,即这个顶点邻域中的任意两个顶点都是相邻的,那么这个顶点被称为单纯形顶点 simplicial vertex,也译为单纯顶点。与所有其他顶点相邻的顶点,被称为泛顶点 universal vertex。
若移除某一顶点(和所有以这个顶点为端点的边)后,图被分离为若干个彼此互不相连的子图,那么这 一顶点就被称为割顶点 cut vertex;由割顶点构成的集合被称为顶点分离集。若一个连通图被移除少于[math]\displaystyle{ k }[/math]个顶点后,总能保持连通,那么这个图被称为[math]\displaystyle{ k-顶点连通图 }[/math]。由两两不相邻的顶点所构成的集合,被称为独立集。由图中每条边的一个或两个端点所构成的集合,被称为顶点覆盖。图的顶点空间是向量空间,它的基向量与图的顶点相对应。
如果一个图具有将任何顶点映射到任何其他顶点的对称性,则该图是顶点传递的。
如果一个图上存在某种自同构映射automorphism [math]\displaystyle{ f: }[/math],能把图中任意一个顶点[math]\displaystyle{ v }[/math]映射为图中的某个其他顶点[math]\displaystyle{ u }[/math] ,同时保持边不变,即若顶点[math]\displaystyle{ v\lt sub\gt 1\lt /sub\gt ,v\lt sub\gt 2\lt /sub\gt }[/math]相邻,那么顶点[math]\displaystyle{ f(v\lt sub\gt 1\lt /sub\gt )=u\lt sub\gt 1\lt /sub\gt }[/math]和[math]\displaystyle{ f(v\lt sub\gt 2\lt /sub\gt )=u\lt sub\gt 2\lt /sub\gt }[/math]也相邻,那么我们认为这个图是顶点传递的,这样的图具有某种相应的对称性质。
在图计数和图同构的语境下,要注意区分有标注的顶点和无标注的顶点。有标注的顶点被关联了额外的信息,以区分这个顶点和其他有标注的顶点;这样一来,只有两个图顶点之间的对应关系是把具有相同标注的顶点配对起来,才能称这两个图是同构的。无标注的顶点,就是只能由其相邻关系而被区分的顶点。
在图计数或者图同构的语境中,若图中的顶点都是无标注的顶点,则可以不用考虑上面那样额外信息的影响。只要两个图之间存在顶点之间的映射[math]\displaystyle{ f: }[/math],使得原来连通的顶点,在映射之后依然连通,就可以说这两个图是同构的。
图的顶点类似于但不等同于(高维)多面体的顶点。但多面体的顶点有额外的结构(几何位置),在图论中未能被假定存在。换句话说,作为概念,图的顶点比多面体的顶点,要更抽象。多面体的骨架构成一个图,其顶点是多面体的顶点,但多面体的顶点有无法在图论中假定存在的其他结构(几何位置) 。多面体中顶点的顶点图形类似于图中顶点的邻域。
参见
参考文献
- ↑ File:Small Network.png; example image of a network with 8 vertices and 10 edges
- Claude Berge|Berge, Claude, Théorie des graphes et ses applications. Collection Universitaire de Mathématiques, II Dunod, Paris 1958, viii+277 pp. (English edition, Wiley 1961; Methuen & Co, New York 1962; Russian, Moscow 1961; Spanish, Mexico 1962; Roumanian, Bucharest 1969; Chinese, Shanghai 1963; Second printing of the 1962 first English edition. Dover, New York 2001)
- Chartrand, Gary (1985). Introductory graph theory. New York: Dover. ISBN 0-486-24775-9. https://archive.org/details/introductorygrap0000char.
- Biggs, Norman; Lloyd, E. H.; Wilson, Robin J. (1986). Graph theory, 1736-1936. Oxford [Oxfordshire]: Clarendon Press. ISBN 0-19-853916-9.
- Harary, Frank (1969). Graph theory. Reading, Mass.: Addison-Wesley Publishing. ISBN 0-201-41033-8.
- Harary, Frank; Palmer, Edgar M. (1973). Graphical enumeration. New York, Academic Press. ISBN 0-12-324245-2.
编辑推荐
集智课程推荐
漫谈图论的起源、发展与应用
本课程中,介绍了图论中的基本概念和网络科学使用的工具,可以帮助认识真实网络的关键性质。
书籍领读:图论
本课程中,将讲解巴拉巴西网络科学书籍第一章图论。
本中文词条由鲁鱼陶阴 参与编译,1220978308 审校,不是海绵宝宝 编辑,欢迎在讨论页面留言。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。