相变

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
跳到导航 跳到搜索

此词条由Jie翻译，由和光同尘审校。


此图显示了不同相变的命名法

The term phase transition (or phase change) is most commonly used to describe transitions between solid, liquid, and gaseous states of matter, as well as plasma in rare cases. A phase of a thermodynamic system and the states of matter have uniform physical properties. During a phase transition of a given medium, certain properties of the medium change, often discontinuously, as a result of the change of external conditions, such as temperature, pressure, or others. For example, a liquid may become gas upon heating to the boiling point, resulting in an abrupt change in volume. The measurement of the external conditions at which the transformation occurs is termed the phase transition. Phase transitions commonly occur in nature and are used today in many technologies.

The term phase transition (or phase change) is most commonly used to describe transitions between solid, liquid, and gaseous states of matter, as well as plasma in rare cases. A phase of a thermodynamic system and the states of matter have uniform physical properties. During a phase transition of a given medium, certain properties of the medium change, often discontinuously, as a result of the change of external conditions, such as temperature, pressure, or others. For example, a liquid may become gas upon heating to the boiling point, resulting in an abrupt change in volume. The measurement of the external conditions at which the transformation occurs is termed the phase transition. Phase transitions commonly occur in nature and are used today in many technologies.

相变Phase transition (or phase change)一词常用于描述物质在固态solid ，液态liquid 和气态gaseous 之间的转变，在极少数情况下还涉及等离子体plasma 。热力学系统的相和物质的状态具有统一的物理属性。由于外部条件（例如温度，压强等）的变化，在给定介质的相变过程中介质的某些属性通常会间断的发生变化。例如，液体在被加热到沸点时可能会变成气体，其体积因此发生突变。综合考量变化发生的外部条件，这种变化被称为相变。相变通常发生在自然界，如今被越来越多地用于科技行业。


Types of phase transition 相变的种类

该图为典型的相图。其中虚线部分表示了水的反常行为

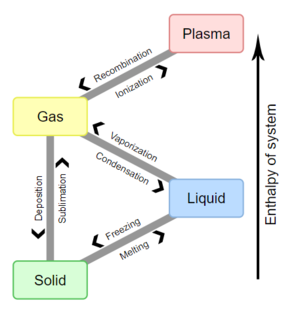
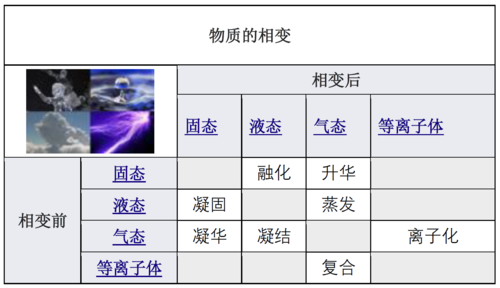
Examples of phase transitions include: Examples of phase transitions include: 相变的例子包括：


  • The transitions between the solid, liquid, and gaseous phases of a single component, due to the effects of temperature and/or pressure:

由于温度和/或压强的影响，单组分在固相，液相和气相之间转换：

参见蒸汽压和相图
一小块固体氩在快速溶解，同时显示出从固体到液体以及从液体到气体的转变。
二氧化碳（红色）和水（蓝色）的相图比较，解释了它们在1个大气压下的不同相变
Condensed matter physics
文件:QuantumPhaseTransition.svg
Phases模板:· Phase transition模板:· QCP
  • A eutectic transformation, in which a two-component single-phase liquid is cooled and transforms into two solid phases. The same process, but beginning with a solid instead of a liquid is called a eutectoid transformation.

共晶转变Eutectic transformation，即互溶液体（由两种不同成分组成的单相液体）经过冷却后转变成为两个不同的固相。如果把互溶液体改成固体，那这一过程就被称为 共析转变 eutectoid transformation。


  • A metastable to equilibrium phase transformation. A metastable polymorph which forms rapidly due to lower surface energy will transform to an equilibrium phase given sufficient thermal input to overcome an energetic barrier.

亚稳态到平衡态的相变。由于较低的表面能而迅速形成的 亚稳多晶体metastable polymorph，在有足以克服能量位垒的热输入时会逐渐转换为一种平衡相。


  • A peritectic transformation, in which a two-component single-phase solid is heated and transforms into a solid phase and a liquid phase.

包晶转变Peritectic transformation。包含两种不同成分的单相固体经过加热后转变为一种固相和一种液相。


  • A spinodal decomposition, in which a single phase is cooled and separates into two different compositions of that same phase.

亚稳相分解Spinodal decomposition。一个单相经过冷却后分离为两种不同的相。


处于固体和液体过渡状态的 中间相mesophase，例如一种“ 液晶liquid crystal”相。


磁性材料处于 居里点Curie point（居里温度）时，在 铁磁ferromagnetism和 顺磁paramagnetism相之间转变。


在以不同方式组织的 相称commensurate或 不相称incommensurate的磁性结构（如在 锑化铈Antimonide中）之间的转变。


马氏体转变Martensitic transformation，作为碳钢的众多相变之一，也是典型的 位移相变displacive phase transformations


晶体结构crystallographic structure 的变化，例如铁在 铁素体Ferrite和 奥氏体Austenite之间的转变。


以α-钛铝化物为例——从有序到无序的转变。


  • The dependence of the adsorption geometry on coverage and temperature, such as for hydrogen on iron (110).

以氢对铁（110）的依赖为例¬——吸附几何结构对覆盖率和温度存在依赖性。


  • The emergence of superconductivity in certain metals and ceramics when cooled below a critical temperature.

当冷却到临界温度以下时，某些金属和陶瓷中出现 超导Superconductivity现象。


  • The transition between different molecular structures (polymorphs, allotropes or polyamorphs), especially of solids, such as between an amorphous structure and a crystal structure, between two different crystal structures, or between two amorphous structures.

不同分子结构（ 同质多形体polymorphs， 同素异形体allotropes或 非晶多形体polyamorphs）之间的转变——特别是固体之间的，例如非晶结构和晶体结构、两种不同晶体结构之间或两种非晶结构之间。


玻色子Bosonic流体的量子凝聚（ 玻色–爱因斯坦凝聚Bose–Einstein condensation）。液态氦中的超流体转变就是一个例子。


  • The breaking of symmetries in the laws of physics during the early history of the universe as its temperature cooled.

物理学中的 对称性破裂breaking of symmetries——发生在宇宙温度降低的早期阶段


  • Isotope fractionation occurs during a phase transition, the ratio of light to heavy isotopes in the involved molecules changes. When water vapor condenses (an equilibrium fractionation), the heavier water isotopes (18O and 2H) become enriched in the liquid phase while the lighter isotopes (16O and 1H) tend toward the vapor phase.

同位素分馏Isotope fractionation发生在相变过程中，所涉及分子的轻同位素与重同位素的比率发生变化。当水蒸气冷凝（平衡分馏equilibrium fractionation ）时，较重的同位素（18O和2H）在液相中富集，而较轻的同位素（16O和1H）则趋向于气相。


Phase transitions occur when the thermodynamic free energy of a system is non-analytic for some choice of thermodynamic variables (cf. phases). This condition generally stems from the interactions of a large number of particles in a system, and does not appear in systems that are too small. It is important to note that phase transitions can occur and are defined for non-thermodynamic systems, where temperature is not a parameter. Examples include: quantum phase transitions, dynamic phase transitions, and topological (structural) phase transitions. In these types of systems other parameters take the place of temperature. For instance, connection probability replaces temperature for percolating networks.

Phase transitions occur when the thermodynamic free energy of a system is non-analytic for some choice of thermodynamic variables (cf. phases). This condition generally stems from the interactions of a large number of particles in a system, and does not appear in systems that are too small. It is important to note that phase transitions can occur and are defined for non-thermodynamic systems, where temperature is not a parameter. Examples include: quantum phase transitions, dynamic phase transitions, and topological (structural) phase transitions. In these types of systems other parameters take the place of temperature. For instance, connection probability replaces temperature for percolating networks.

当系统的热力学自由能无法对某些热力学变量进行解析时，相变就会发生。这通常是因为系统中存在大量相互作用的粒子。如果系统太小，则不会出现。值得注意的是，相变同样可以存在于参数不包括温度的非热力学系统中。例如：量子相变，动态相变和拓扑（结构）相变。在这些系统中，其他参数代替了温度（在 渗滤网络percolating networks中，连接概率代替温度）。


At the phase transition point (for instance, boiling point) the two phases of a substance, liquid and vapor, have identical free energies and therefore are equally likely to exist. Below the boiling point, the liquid is the more stable state of the two, whereas above the gaseous form is preferred.

At the phase transition point (for instance, boiling point) the two phases of a substance, liquid and vapor, have identical free energies and therefore are equally likely to exist. Below the boiling point, the liquid is the more stable state of the two, whereas above the gaseous form is preferred.

物质的两个相（液相和气相）在相变点（如沸点）具有相同的自由能，因此它们存在的可能性相同。而当温度低于沸点时，液态在两者中更稳定；当温度高于沸点时，气态更具优势。


It is sometimes possible to change the state of a system diabatically (as opposed to adiabatically) in such a way that it can be brought past a phase transition point without undergoing a phase transition. The resulting state is metastable, i.e., less stable than the phase to which the transition would have occurred, but not unstable either. This occurs in superheating, supercooling, and supersaturation, for example.

It is sometimes possible to change the state of a system diabatically (as opposed to adiabatically) in such a way that it can be brought past a phase transition point without undergoing a phase transition. The resulting state is metastable, i.e., less stable than the phase to which the transition would have occurred, but not unstable either. This occurs in superheating, supercooling, and supersaturation, for example.

有时系统状态可以通过传热方式（与绝热方式相对）改变，这使系统状态得以通过相变点而又不经历相变。此时该系统会处于亚稳态（与发生了相变的相相比，其状态没有那么稳定，但也并非不稳定）。过热、过冷以及过饱和时都会发生这种现象。

Classifications 分类

Ehrenfest classification 埃伦费斯特分类法

Paul Ehrenfest classified phase transitions based on the behavior of the thermodynamic free energy as a function of other thermodynamic variables. Under this scheme, phase transitions were labeled by the lowest derivative of the free energy that is discontinuous at the transition. First-order phase transitions exhibit a discontinuity in the first derivative of the free energy with respect to some thermodynamic variable. The various solid/liquid/gas transitions are classified as first-order transitions because they involve a discontinuous change in density, which is the (inverse of the) first derivative of the free energy with respect to pressure. Second-order phase transitions are continuous in the first derivative (the order parameter, which is the first derivative of the free energy with respect to the external field, is continuous across the transition) but exhibit discontinuity in a second derivative of the free energy. These include the ferromagnetic phase transition in materials such as iron, where the magnetization, which is the first derivative of the free energy with respect to the applied magnetic field strength, increases continuously from zero as the temperature is lowered below the Curie temperature. The magnetic susceptibility, the second derivative of the free energy with the field, changes discontinuously. Under the Ehrenfest classification scheme, there could in principle be third, fourth, and higher-order phase transitions.

Paul Ehrenfest classified phase transitions based on the behavior of the thermodynamic free energy as a function of other thermodynamic variables. Under this scheme, phase transitions were labeled by the lowest derivative of the free energy that is discontinuous at the transition. First-order phase transitions exhibit a discontinuity in the first derivative of the free energy with respect to some thermodynamic variable. The various solid/liquid/gas transitions are classified as first-order transitions because they involve a discontinuous change in density, which is the (inverse of the) first derivative of the free energy with respect to pressure. Second-order phase transitions are continuous in the first derivative (the order parameter, which is the first derivative of the free energy with respect to the external field, is continuous across the transition) but exhibit discontinuity in a second derivative of the free energy. These include the ferromagnetic phase transition in materials such as iron, where the magnetization, which is the first derivative of the free energy with respect to the applied magnetic field strength, increases continuously from zero as the temperature is lowered below the Curie temperature. The magnetic susceptibility, the second derivative of the free energy with the field, changes discontinuously. Under the Ehrenfest classification scheme, there could in principle be third, fourth, and higher-order phase transitions.

保罗·埃伦费斯特Paul Ehrenfest根据热力学自由能和其他热力学变量的函数关系对相变进行了分类。根据他的方法，可以按照转变时的不连续自由能最低导数标记相变。一阶相变first-order phase transitions相对于某些热力学变量，具有自由能的一阶导数不连续性。我们将各种固/液/气的转变都归为一阶相变，因为它们都涉及到密度的不连续变化——这是自由能相对于压力的一阶导数（一阶导数的逆函数）。而 二阶相变second-order phase transitions在一阶导数中是连续的（有序参数，即自由能相对于外部场的一阶导数，在整个转变过程中是连续的），但在自由能的二阶导数中表现出不连续性。比如铁磁相变ferromagnetic transition （发生在铁等材料中），其中磁化强度是自由能相对于施加磁场强度的一阶导数。随着温度降低到居里温度以下，磁化强度将从零开始持续增加。而磁化率，是自由能相对于磁场的二阶导数，它的变化是不连续的。以此类推，按照Ehrenfest的分类方法，原则上可以存在第三，第四甚至更高阶的相变。


The Ehrenfest classification implicitly allows for continuous phase transformations, where the bonding character of a material changes, but there is no discontinuity in any free energy derivative. An example of this occurs at the supercritical liquid–gas boundaries.

The Ehrenfest classification implicitly allows for continuous phase transformations, where the bonding character of a material changes, but there is no discontinuity in any free energy derivative. An example of this occurs at the supercritical liquid–gas boundaries.

埃伦费斯特分类法Ehrenfest classification隐含连续相变，其中材料的成键特征发生了变化，但任何自由能导数都没有间断。比如说超临界液气的边界。


Modern classifications 现代分类法

In the modern classification scheme, phase transitions are divided into two broad categories, named similarly to the Ehrenfest classes:

In the modern classification scheme, phase transitions are divided into two broad categories, named similarly to the Ehrenfest classes:

在现代分类方案中，相变被分为两大类，命名方式类似于埃伦费斯特分类法：


First-order phase transitions are those that involve a latent heat. During such a transition, a system either absorbs or releases a fixed (and typically large) amount of energy per volume. During this process, the temperature of the system will stay constant as heat is added: the system is in a "mixed-phase regime" in which some parts of the system have completed the transition and others have not. Familiar examples are the melting of ice or the boiling of water (the water does not instantly turn into vapor, but forms a turbulent mixture of liquid water and vapor bubbles). Imry and Wortis showed that quenched disorder can broaden a first-order transition. That is, the transformation is completed over a finite range of temperatures, but phenomena like supercooling and superheating survive and hysteresis is observed on thermal cycling.

First-order phase transitions are those that involve a latent heat. During such a transition, a system either absorbs or releases a fixed (and typically large) amount of energy per volume. During this process, the temperature of the system will stay constant as heat is added: the system is in a "mixed-phase regime" in which some parts of the system have completed the transition and others have not. Familiar examples are the melting of ice or the boiling of water (the water does not instantly turn into vapor, but forms a turbulent mixture of liquid water and vapor bubbles). Imry and Wortis showed that quenched disorder can broaden a first-order transition. That is, the transformation is completed over a finite range of temperatures, but phenomena like supercooling and superheating survive and hysteresis is observed on thermal cycling.

一阶相变是那些涉及潜伏热的相变。在这种相变过程中，系统会吸收或释放固定（通常是大量）的能量。在此过程中，即使热量增加，系统的温度也保持恒定：系统处于“混合相状态”，也就是说某些部分已完成转变，而其他部分尚未完成。常见的例子是冰的融化或水的沸腾（水不会立即变成蒸气，而是成为液态水和蒸气气泡的湍流混合物）。物理学家伊姆利 Imry和沃迪斯 Wortis研究发现，可以将 淬火无序quenched disorder视为一阶转变。即在有限的温度范围内完成相变，但是过冷或过热现象仍然存在，并且滞后仍然存在于热循环中。


Second-order phase transitions are also called "continuous phase transitions". They are characterized by a divergent susceptibility, an infinite correlation length, and a power law decay of correlations near criticality. Examples of second-order phase transitions are the ferromagnetic transition, superconducting transition (for a Type-I superconductor the phase transition is second-order at zero external field and for a Type-II superconductor the phase transition is second-order for both normal-state—mixed-state and mixed-state—superconducting-state transitions) and the superfluid transition. In contrast to viscosity, thermal expansion and heat capacity of amorphous materials show a relatively sudden change at the glass transition temperature which enables accurate detection using differential scanning calorimetry measurements. Lev Landau gave a phenomenological theory of second-order phase transitions.

Second-order phase transitions are also called "continuous phase transitions". They are characterized by a divergent susceptibility, an infinite correlation length, and a power law decay of correlations near criticality. Examples of second-order phase transitions are the ferromagnetic transition, superconducting transition (for a Type-I superconductor the phase transition is second-order at zero external field and for a Type-II superconductor the phase transition is second-order for both normal-state—mixed-state and mixed-state—superconducting-state transitions) and the superfluid transition. In contrast to viscosity, thermal expansion and heat capacity of amorphous materials show a relatively sudden change at the glass transition temperature which enables accurate detection using differential scanning calorimetry measurements. Lev Landau gave a phenomenological theory of second-order phase transitions.

二阶相变Second-order phase transitions ，或称为“连续相变”，它们的特征是敏感度发散，相关长度无限以及接近临界的相关性幂律衰减。二阶相变的例子是铁磁相变，超导相变superconducting transition （对于I型超导体，在零外场下的相变是二阶的;对于II型超导体，从常态到混合态以及混合态到超导状态的转变都是二阶的）和超流体转换superfluid transition 。另外，对非晶体材料amorphous materials而言，热膨胀thermal expansion和热容属性heat capacity在玻璃相变温度下会发生突变——这与粘度属性相反。我们可以使用差示扫描量热法来精确检测变化数值。列夫·兰道Lev Landau后来得出了二阶相变的现象学理论。


Apart from isolated, simple phase transitions, there exist transition lines as well as multicritical points, when varying external parameters like the magnetic field or composition.

Apart from isolated, simple phase transitions, there exist transition lines as well as multicritical points, when varying external parameters like the magnetic field or composition.

当改变诸如磁场、成分之类的外部参数时，除了独立、简单的相变，还存在跃迁谱线transition lines以及多个临界点multicritical points。


Several transitions are known as infinite-order phase transitions.They are continuous but break no symmetries. The most famous example is the Kosterlitz–Thouless transition in the two-dimensional XY model. Many quantum phase transitions, e.g., in two-dimensional electron gases, belong to this class.

Several transitions are known as infinite-order phase transitions.They are continuous but break no symmetries. The most famous example is the Kosterlitz–Thouless transition in the two-dimensional XY model. Many quantum phase transitions, e.g., in two-dimensional electron gases, belong to this class.

另外还存在其他相变类型,例如无限阶相变 infinite-order phase transitions。无限阶相变是连续的,但并不破坏对称性。最著名的例子是二维XY模型中的KS相变 Kosterlitz-Thouless transition。除此之外, 二维电子气two-dimensional electron gases 中的量子相变也属于无限阶相变。


The liquid–glass transition is observed in many polymers and other liquids that can be supercooled far below the melting point of the crystalline phase. This is atypical in several respects. It is not a transition between thermodynamic ground states: it is widely believed that the true ground state is always crystalline. Glass is a quenched disorder state, and its entropy, density, and so on, depend on the thermal history. Therefore, the glass transition is primarily a dynamic phenomenon: on cooling a liquid, internal degrees of freedom successively fall out of equilibrium. Some theoretical methods predict an underlying phase transition in the hypothetical limit of infinitely long relaxation times. No direct experimental evidence supports the existence of these transitions.

The liquid–glass transition is observed in many polymers and other liquids that can be supercooled far below the melting point of the crystalline phase. This is atypical in several respects. It is not a transition between thermodynamic ground states: it is widely believed that the true ground state is always crystalline. Glass is a quenched disorder state, and its entropy, density, and so on, depend on the thermal history. Therefore, the glass transition is primarily a dynamic phenomenon: on cooling a liquid, internal degrees of freedom successively fall out of equilibrium. Some theoretical methods predict an underlying phase transition in the hypothetical limit of infinitely long relaxation times. No direct experimental evidence supports the existence of these transitions.

在被冷却至远低于结晶相熔点的聚合物和其他液体中出现了液体-玻璃相变liquid–glass transition。综合考虑多个方面，我们认为这是一种非典型相变。它不是热力学基态之间的转变：因为人们普遍认为，真正的基态始终是晶体。玻璃是淬火无序状态，其熵entropy、密度density等取决于热历史。因此，可以把玻璃相变看作一种动态现象：液体冷却时，其内部自由度会逐渐失去平衡。一些理论预测其潜在相变会发生在无限长弛豫时间relaxation times的假设极限内。但是目前并不存在直接的实验证据来支持其存在。


The gelation transition of colloidal particles has been shown to be a second-order phase transition under nonequilibrium conditions. 在非平衡条件下，胶体粒子colloidal particles的凝胶化转变被认为是二级相变。

Characteristic properties 特征属性

Phase coexistence 相共存

A disorder-broadened first-order transition occurs over a finite range of temperatures where the fraction of the low-temperature equilibrium phase grows from zero to one (100%) as the temperature is lowered. This continuous variation of the coexisting fractions with temperature raised interesting possibilities. On cooling, some liquids vitrify into a glass rather than transform to the equilibrium crystal phase. This happens if the cooling rate is faster than a critical cooling rate, and is attributed to the molecular motions becoming so slow that the molecules cannot rearrange into the crystal positions. If the first-order freezing transition occurs over a range of temperatures, and Tg falls within this range, then there is an interesting possibility that the transition is arrested when it is partial and incomplete. Extending these ideas to first-order magnetic transitions being arrested at low temperatures, resulted in the observation of incomplete magnetic transitions, with two magnetic phases coexisting, down to the lowest temperature. First reported in the case of a ferromagnetic to anti-ferromagnetic transition, such persistent phase coexistence has now been reported across a variety of first-order magnetic transitions. These include colossal-magnetoresistance manganite materials,magnetocaloric materials,magnetic shape memory materials,The interesting feature of these observations of Tg falling within the temperature range over which the transition occurs is that the first-order magnetic transition is influenced by magnetic field, just like the structural transition is influenced by pressure. The relative ease with which magnetic fields can be controlled, in contrast to pressure, raises the possibility that one can study the interplay between Tg and Tc in an exhaustive way. Phase coexistence across first-order magnetic transitions will then enable the resolution of outstanding issues in understanding glasses.


A disorder-broadened first-order transition occurs over a finite range of temperatures where the fraction of the low-temperature equilibrium phase grows from zero to one (100%) as the temperature is lowered. This continuous variation of the coexisting fractions with temperature raised interesting possibilities. On cooling, some liquids vitrify into a glass rather than transform to the equilibrium crystal phase. This happens if the cooling rate is faster than a critical cooling rate, and is attributed to the molecular motions becoming so slow that the molecules cannot rearrange into the crystal positions. This slowing down happens below a glass-formation temperature Tg, which may depend on the applied pressure. If the first-order freezing transition occurs over a range of temperatures, and Tg falls within this range, then there is an interesting possibility that the transition is arrested when it is partial and incomplete. Extending these ideas to first-order magnetic transitions being arrested at low temperatures, resulted in the observation of incomplete magnetic transitions, with two magnetic phases coexisting, down to the lowest temperature. First reported in the case of a ferromagnetic to anti-ferromagnetic transition, such persistent phase coexistence has now been reported across a variety of first-order magnetic transitions. These include colossal-magnetoresistance manganite materials, magnetocaloric materials, magnetic shape memory materials, and other materials.The interesting feature of these observations of Tg falling within the temperature range over which the transition occurs is that the first-order magnetic transition is influenced by magnetic field, just like the structural transition is influenced by pressure. The relative ease with which magnetic fields can be controlled, in contrast to pressure, raises the possibility that one can study the interplay between Tg and Tc in an exhaustive way. Phase coexistence across first-order magnetic transitions will then enable the resolution of outstanding issues in understanding glasses.

在有限的温度范围内，胶体粒子的凝胶化转变显示为bA紊乱-扩展的一阶转变。随着温度降低，低温平衡相low-temperature equilibrium phase的分数从零增加到一（100％）。随温度变化而变化的馏分共存创造了许多有趣的可能性。比如在冷却时，一些液体会逐渐玻璃化，而不是转变为平衡晶相equilibrium crystal phase。这种情况往往发生在冷却速率比临界冷却速率快的时候——分子运动变得十分缓慢，以至于分子无法重新排列到晶体位置。分子运动的减速通常发生在气温降至玻璃的形成温度Tg以下时——这可能需要外部施加压力来实现。如果Tg落在该一阶冻结相变发生的特定温度范围内，一种有趣的现象就会发生，即当转变不完整时该转变会停止。同理可以考虑在低温下被阻止的一阶磁相变，我们可以观察到不完全的磁相变，即两个磁相同时存在直至到达最低温度。自关于铁磁到反铁磁相变的报道首次公开以来，人们逐渐发现了各种一阶磁相变的持久相共存现象。包括庞磁电阻锰矿材料colossal-magnetoresistance manganite materials、磁制冷材料magnetocaloric materials、磁性形状记忆材料magnetic shape memory materials等。当Tg落在相变发生的温度范围内时，观测结果非常有趣，其一阶磁相变受到了磁场的影响——就像结构相变会受到压力影响一样。不过与压力相比，控制磁场相对容易，这大大提高了研究者们运用穷举法研究Tg和Tc之间相互作用的成功率。一阶磁相变的相位共存将有助于解决和玻璃有关的一系列突出问题。


Critical points 临界点

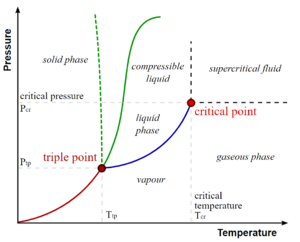
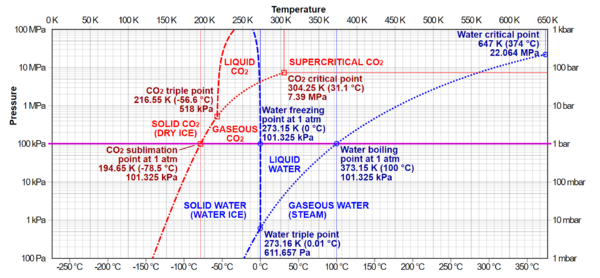
In any system containing liquid and gaseous phases, there exists a special combination of pressure and temperature, known as the critical point, at which the transition between liquid and gas becomes a second-order transition. Near the critical point, the fluid is sufficiently hot and compressed that the distinction between the liquid and gaseous phases is almost non-existent. This is associated with the phenomenon of critical opalescence, a milky appearance of the liquid due to density fluctuations at all possible wavelengths (including those of visible light).

In any system containing liquid and gaseous phases, there exists a special combination of pressure and temperature, known as the critical point, at which the transition between liquid and gas becomes a second-order transition. Near the critical point, the fluid is sufficiently hot and compressed that the distinction between the liquid and gaseous phases is almost non-existent. This is associated with the phenomenon of critical opalescence, a milky appearance of the liquid due to density fluctuations at all possible wavelengths (including those of visible light).

在任何包含液相和气相的系统中都存在压力和温度的特殊组合，我们称之为临界点。在该临界点处，液相和气相之间的转变即为二级相变。在临界点附近，如果流体足够热并且被压缩，那么液相和气相之间的区别几乎就消失了。这与临界乳光现象有关——液体在所有可能的波长（包括可见光）处产生密度波动，变成乳白色。


Symmetry 对称性

Phase transitions often involve a symmetry breaking process. For instance, the cooling of a fluid into a crystalline solid breaks continuous translation symmetry: each point in the fluid has the same properties, but each point in a crystal does not have the same properties (unless the points are chosen from the lattice points of the crystal lattice). Typically, the high-temperature phase contains more symmetries than the low-temperature phase due to spontaneous symmetry breaking, with the exception of certain accidental symmetries (e.g. the formation of heavy virtual particles, which only occurs at low temperatures).

Phase transitions often involve a symmetry breaking process. For instance, the cooling of a fluid into a crystalline solid breaks continuous translation symmetry: each point in the fluid has the same properties, but each point in a crystal does not have the same properties (unless the points are chosen from the lattice points of the crystal lattice). Typically, the high-temperature phase contains more symmetries than the low-temperature phase due to spontaneous symmetry breaking, with the exception of certain accidental symmetries (e.g. the formation of heavy virtual particles, which only occurs at low temperatures).

相变通常涉及到对称破坏。例如，将流体冷却至成结晶固体会破坏其连续的平移对称性：流体中的每个点都具有相同的属性，但是晶体中的点并非如此（除非这些点来自晶格点阵中的晶格点）。通常，由于 自发对称性破缺spontaneous symmetry breaking，除了某些特殊的对称性（例如， 重虚粒子Virtual particles的形成，其仅在低温下发生）外，高温相比低温相具有更多的对称性。


Order parameters 序参数

An order parameter is a measure of the degree of order across the boundaries in a phase transition system; it normally ranges between zero in one phase (usually above the critical point) and nonzero in the other. At the critical point, the order parameter susceptibility will usually diverge.

An order parameter is a measure of the degree of order across the boundaries in a phase transition system; it normally ranges between zero in one phase (usually above the critical point) and nonzero in the other. At the critical point, the order parameter susceptibility will usually diverge.

序参数Order parameter是相变系统中跨边界的有序/无序度量；它通常在一个为零的阶段（通常在临界点以上）和一个非零阶段之间。在临界点，序参数的敏感性通常会有分离趋向。


An example of an order parameter is the net magnetization in a ferromagnetic system undergoing a phase transition. For liquid/gas transitions, the order parameter is the difference of the densities.

An example of an order parameter is the net magnetization in a ferromagnetic system undergoing a phase transition. For liquid/gas transitions, the order parameter is the difference of the densities.

序参数的一个示例是发生相变的铁磁系统中的净磁化强度。对于液/气相而言，序参数就是它们的密度之差。


From a theoretical perspective, order parameters arise from symmetry breaking. When this happens, one needs to introduce one or more extra variables to describe the state of the system. For example, in the ferromagnetic phase, one must provide the net magnetization, whose direction was spontaneously chosen when the system cooled below the Curie point. However, note that order parameters can also be defined for non-symmetry-breaking transitions.

From a theoretical perspective, order parameters arise from symmetry breaking. When this happens, one needs to introduce one or more extra variables to describe the state of the system. For example, in the ferromagnetic phase, one must provide the net magnetization, whose direction was spontaneously chosen when the system cooled below the Curie point. However, note that order parameters can also be defined for non-symmetry-breaking transitions.

从理论的角度来看，序参数来自对称性破坏。当发生这种情况时，需要引入一个或多个他变量来描述该系统状态。例如，在铁磁相中必须提供净磁化强度，因为当系统降温至居里点以下时，磁化方向会自动确定。但是值得注意的是，非对称性破坏相变也可以定义有序参数。


Some phase transitions, such as superconducting and ferromagnetic, can have order parameters for more than one degree of freedom. In such phases, the order parameter may take the form of a complex number, a vector, or even a tensor, the magnitude of which goes to zero at the phase transition.

Some phase transitions, such as superconducting and ferromagnetic, can have order parameters for more than one degree of freedom. In such phases, the order parameter may take the form of a complex number, a vector, or even a tensor, the magnitude of which goes to zero at the phase transition.

某些相变，例如 超导superconducting和铁磁，可以具有超过一个自由度的多个序参数。在这样的相中，序参数可以采用复数、向量vector甚至张量tensor的形式，其大小在相变发生时会变为零。


There also exist dual descriptions of phase transitions in terms of disorder parameters. These indicate the presence of line-like excitations such as vortex- or defect lines.

There also exist dual descriptions of phase transitions in terms of disorder parameters. These indicate the presence of line-like excitations such as vortex- or defect lines.

无序参数disorder parameters中存在着相变的双重表述。 这就证明了 线状激励line-like excitations确实存在，例如 涡旋线vortex lines， 缺陷线defect lines等。


Relevance in cosmology 宇宙学的相关性

Symmetry-breaking phase transitions play an important role in cosmology. As the universe expanded and cooled, the vacuum underwent a series of symmetry-breaking phase transitions. For example, the electroweak transition broke the SU(2)×U(1) symmetry of the electroweak field into the U(1) symmetry of the present-day electromagnetic field. This transition is important to understanding the asymmetry between the amount of matter and antimatter in the present-day universe (see electroweak baryogenesis).

Symmetry-breaking phase transitions play an important role in cosmology. As the universe expanded and cooled, the vacuum underwent a series of symmetry-breaking phase transitions. For example, the electroweak transition broke the SU(2)×U(1) symmetry of the electroweak field into the U(1) symmetry of the present-day electromagnetic field. This transition is important to understanding the asymmetry between the amount of matter and antimatter in the present-day universe (see electroweak baryogenesis).

对称性破坏相变在宇宙学中起着重要作用。随着宇宙的膨胀和冷却，太空经历了一系列对称性破坏的相变。例如，电弱过渡破坏了当时电弱场的SU（2）×U（1）对称性，生成了当今电磁场的U（1）对称性。一旦明白宇宙发生过这种转变，对当今宇宙中物质与反物质之间不对称性的研究对我们来说也就更好理解了（请参阅 弱电重子生成electroweak baryogenesis）。


Progressive phase transitions in an expanding universe are implicated in the development of order in the universe, as is illustrated by the work of Eric Chaisson and David Layzer.

Progressive phase transitions in an expanding universe are implicated in the development of order in the universe, as is illustrated by the work of Eric Chaisson and David Layzer.

埃里克·蔡森Eric Chaisson和戴维·莱泽David Layzer的研究表明，相变正在不断膨胀的宇宙中进行，这与宇宙秩序的发展变化有关。


See also relational order theories and order and disorder.

See also relational order theories and order and disorder.

详情另参见关系秩序理论relational order theories和秩序与无序。


Critical exponents and universality classes 临界指数和普适性

Continuous phase transitions are easier to study than first-order transitions due to the absence of latent heat, and they have been discovered to have many interesting properties. The phenomena associated with continuous phase transitions are called critical phenomena, due to their association with critical points.

Continuous phase transitions are easier to study than first-order transitions due to the absence of latent heat, and they have been discovered to have many interesting properties. The phenomena associated with continuous phase transitions are called critical phenomena, due to their association with critical points.

由于不存在 潜伏热latent heat，连续相变比一阶相变更容易研究。目前人们已经发现了许多有趣的性质。与连续相变有关的现象由于与临界点有关而被称为临界现象。


It turns out that continuous phase transitions can be characterized by parameters known as critical exponents. The most important one is perhaps the exponent describing the divergence of the thermal correlation length by approaching the transition. For instance, let us examine the behavior of the heat capacity near such a transition. We vary the temperature T of the system while keeping all the other thermodynamic variables fixed, and find that the transition occurs at some critical temperature Tc . When T is near Tc , the heat capacity C typically has a power law behavior,

It turns out that continuous phase transitions can be characterized by parameters known as critical exponents. The most important one is perhaps the exponent describing the divergence of the thermal correlation length by approaching the transition. For instance, let us examine the behavior of the heat capacity near such a transition. We vary the temperature of the system while keeping all the other thermodynamic variables fixed, and find that the transition occurs at some critical temperature Tc . When is near Tc , the heat capacity typically has a power law behavior,

事实证明，连续相变可以由临界指数critical exponents这一参数表征。其中最重要的一个参数也许是描述逼近相变时热相关长度差异的指数。例如，让我们检测相变即将发生时的热容行为。在保持其他所有热力学变量不变的条件下，改变系统温度T，发现相变发生在某个临界温度Tc处。当T接近Tc时，热容C通常具有幂律行为power law behavior：

[math]\displaystyle{ C \propto |T_c - T|^{-\alpha}. }[/math]

The heat capacity of amorphous materials has such a behaviour near the glass transition temperature where the universal critical exponent α = 0.59 A similar behavior, but with the exponent ν instead of α, applies for the correlation length.

The heat capacity of amorphous materials has such a behaviour near the glass transition temperature where the universal critical exponent α = 0.59 A similar behavior, but with the exponent instead of , applies for the correlation length.

当接近玻璃相变温度时，非晶体材料的热容会具有幂律行为，其中通用临界指数α= 0.59。这也适用于相关长度，但要将指数改为ν。


The exponent ν is positive. This is different with α. Its actual value depends on the type of phase transition we are considering.

The exponent is positive. This is different with . Its actual value depends on the type of phase transition we are considering.

指数ν为正数，这与α不同。临界指数的实际值取决于我们选择的相变类型。


It is widely believed that the critical exponents are the same above and below the critical temperature. It has now been shown that this is not necessarily true: When a continuous symmetry is explicitly broken down to a discrete symmetry by irrelevant (in the renormalization group sense) anisotropies, then some exponents (such as [math]\displaystyle{ \gamma }[/math], the exponent of the susceptibility) are not identical.

It is widely believed that the critical exponents are the same above and below the critical temperature. It has now been shown that this is not necessarily true: When a continuous symmetry is explicitly broken down to a discrete symmetry by irrelevant (in the renormalization group sense) anisotropies, then some exponents (such as [math]\displaystyle{ \gamma }[/math], the exponent of the susceptibility) are not identical.

人们曾普遍认为，不管温度在临界温度之上还是临界温度之下，临界指数保持不变。但是现实证明这不一定正确：当连续对称属性因不相关的各向异性anisotropies（在重整化群理论renormalization group意义上）而分解为离散对称属性时，某些指数（例如γ， 磁化率指数Exponent of the susceptibility）会有所不同。


For −1 < α < 0, the heat capacity has a "kink" at the transition temperature. This is the behavior of liquid helium at the lambda transition from a normal state to the superfluid state, for which experiments have found α = -0.013±0.003.At least one experiment was performed in the zero-gravity conditions of an orbiting satellite to minimize pressure differences in the sample.This experimental value of α agrees with theoretical predictions based on variational perturbation theory.

For −1 < α < 0, the heat capacity has a "kink" at the transition temperature. This is the behavior of liquid helium at the lambda transition from a normal state to the superfluid state, for which experiments have found = -0.013±0.003.At least one experiment was performed in the zero-gravity conditions of an orbiting satellite to minimize pressure differences in the sample. This experimental value of α agrees with theoretical predictions based on variational perturbation theory.

当-1 <α<0时，热容在相变温度下具有“扭结”性质。这是液氦liquid helium从正常状态到超流体状态的λ相变行为，在此实验中发现α= -0.013±0.003。为最小化样品中的压力差，至少有一次实验在轨道卫星的零重力条件下进行。α的这个实验值与基于变分微扰理论variational perturbation theory的预测值相符。


For 0 < α < 1, the heat capacity diverges at the transition temperature (though, since α < 1, the enthalpy stays finite). An example of such behavior is the 3D ferromagnetic phase transition. In the three-dimensional Ising model for uniaxial magnets, detailed theoretical studies have yielded the exponent α ∼ +0.110.

For 0 < < 1, the heat capacity diverges at the transition temperature (though, since < 1, the enthalpy stays finite). An example of such behavior is the 3D ferromagnetic phase transition. In the three-dimensional Ising model for uniaxial magnets, detailed theoretical studies have yielded the exponent ∼ +0.110.

当0 <α<1时，热容在相变温度处发散（也因为α<1，所以焓保持有限）。例如3D铁磁相变 3D ferromagnetic phase transition。运用单轴磁体uniaxial magnets的三维伊辛模型three-dimensional Ising model，研究人员通过详细的理论研究得出指数α≈+0.110。


Some model systems do not obey a power-law behavior. For example, mean field theory predicts a finite discontinuity of the heat capacity at the transition temperature, and the two-dimensional Ising model has a logarithmic divergence. However, these systems are limiting cases and an exception to the rule. Real phase transitions exhibit power-law behavior.

Some model systems do not obey a power-law behavior. For example, mean field theory predicts a finite discontinuity of the heat capacity at the transition temperature, and the two-dimensional Ising model has a logarithmic divergence. However, these systems are limiting cases and an exception to the rule. Real phase transitions exhibit power-law behavior.

当然，存在一些不遵循幂律行为的模型系统。例如，平均场理论预测了相变温度下热容量的有限不连续性，而二维伊辛模型two-dimensional lsing model则具有对数散度。但是，这样的系统数量有限，是例外。实际上大多相变仍然表现出幂律行为。


Several other critical exponents, β, γ, δ, ν, and η, are defined, examining the power law behavior of a measurable physical quantity near the phase transition. Exponents are related by scaling relations, such as

Several other critical exponents, , and , are defined, examining the power law behavior of a measurable physical quantity near the phase transition. Exponents are related by scaling relations, such as

另外还存在其他几个临界指数β，γ，δ，ν和η，主要用于检查相变附近可测物理量的幂律行为。它们通过比例关系相互联系，例如：

[math]\displaystyle{ \beta=\gamma/(\delta-1) , \qquad \nu=\gamma/(2-\eta) }[/math].

It can be shown that there are only two independent exponents, e.g. ν and η. It can be shown that there are only two independent exponents, e.g. and . 上式可以证明只有两个独立的指数，例如 ν和η。


It is a remarkable fact that phase transitions arising in different systems often possess the same set of critical exponents. This phenomenon is known as universality. For example, the critical exponents at the liquid–gas critical point have been found to be independent of the chemical composition of the fluid.

It is a remarkable fact that phase transitions arising in different systems often possess the same set of critical exponents. This phenomenon is known as universality. For example, the critical exponents at the liquid–gas critical point have been found to be independent of the chemical composition of the fluid.

值得注意的是，在不同系统中发生的相变通常具有相同的临界指数。我们称这种现象为普适性universality。例如，液气临界点的临界指数与流体的化学组成无关。


More impressively, but understandably from above, they are an exact match for the critical exponents of the ferromagnetic phase transition in uniaxial magnets. Such systems are said to be in the same universality class. Universality is a prediction of the renormalization group theory of phase transitions, which states that the thermodynamic properties of a system near a phase transition depend only on a small number of features, such as dimensionality and symmetry, and are insensitive to the underlying microscopic properties of the system. Again, the divergence of the correlation length is the essential point.

More impressively, but understandably from above, they are an exact match for the critical exponents of the ferromagnetic phase transition in uniaxial magnets. Such systems are said to be in the same universality class. Universality is a prediction of the renormalization group theory of phase transitions, which states that the thermodynamic properties of a system near a phase transition depend only on a small number of features, such as dimensionality and symmetry, and are insensitive to the underlying microscopic properties of the system. Again, the divergence of the correlation length is the essential point.

以上现象很特别，但并非无法理解，它们与单轴磁体中铁磁相变的临界指数完全匹配。人们认为这类系统具有同一普适性。这里的普适性是相变的重整化群理论的一种预测，指出系统在即将相变时的热力学性质仅取决于少数几个特征，例如维数dimensionality和对称性symmetry，对系统的基本微观特性并不敏感。同样，相关长度的差异性也是非常重要的因素。

Critical slowing down and other phenomena 临界慢化和其他现象

There are also other critical phenomena; e.g., besides static functions there is also critical dynamics. As a consequence, at a phase transition one may observe critical slowing down or speeding up. The large static universality classes of a continuous phase transition split into smaller dynamic universality classes. In addition to the critical exponents, there are also universal relations for certain static or dynamic functions of the magnetic fields and temperature differences from the critical value.

There are also other critical phenomena; e.g., besides static functions there is also critical dynamics. As a consequence, at a phase transition one may observe critical slowing down or speeding up. The large static universality classes of a continuous phase transition split into smaller dynamic universality classes. In addition to the critical exponents, there are also universal relations for certain static or dynamic functions of the magnetic fields and temperature differences from the critical value.

在相变过程中，还存在其他临界现象。例如，除了静态函数static functions外，还存在临界动态。因此在相变发生时，人们可能会观察到明显的减速或加速现象。连续相变的静态普适性可以被分成更小的动态普适性。除了临界指，磁场的某些静态或动态函数以及与临界值的温差也存在普适性关系。


Percolation theory 渗流理论

Another phenomenon which shows phase transitions and critical exponents is percolation. The simplest example is perhaps percolation in a two dimensional square lattice. Sites are randomly occupied with probability p. For small values of p the occupied sites form only small clusters. At a certain threshold pc a giant cluster is formed and we have a second-order phase transition. The behavior of P∞ near pc is, P∞~(p-pc)β, where β is a critical exponent.

Another phenomenon which shows phase transitions and critical exponents is percolation. The simplest example is perhaps percolation in a two dimensional square lattice. Sites are randomly occupied with probability p. For small values of p the occupied sites form only small clusters. At a certain threshold pc a giant cluster is formed and we have a second-order phase transition. The behavior of P∞ near pc is, P∞~(p-pc)β, where β is a critical exponent.

渗流percolation具有临界指数，能够发生相变。最简单的例子是发生在二维方格中的渗流。其中每一个格子以概率p标记。对于较小的p值，格子就形成较小的团簇clusters。但是当p达到某个阈值Pc时就会出现一个巨大的团簇，此时发生二阶相变。Pc附近的P∞行为是P∞〜（p − pc）β——其中β是一个临界指数。


Phase transitions in biological systems 生物系统中的相变

Phase transitions play many important roles in biological systems. Examples include the lipid bilayer formation, the coil-globule transition in the process of protein folding and DNA melting, liquid crystal-like transitions in the process of DNA condensation, and cooperative ligand binding to DNA and proteins with the character of phase transition.

Phase transitions play many important roles in biological systems. Examples include the lipid bilayer formation, the coil-globule transition in the process of protein folding and DNA melting, liquid crystal-like transitions in the process of DNA condensation, and cooperative ligand binding to DNA and proteins with the character of phase transition.

相变在生物系统中也具有重要的作用。比如 脂质双层lipid bilayer的形成， 蛋白质折叠protein folding和 DNA解链DNA melting过程中的 坍塌转变coil–globule transition， DNA缩合DNA condensation过程中的液晶转变，以及具有相变特征的配体与DNA和蛋白质的结合。


In biological membranes, gel to liquid crystalline phase transitions play a critical role in physiological functioning of biomembranes. In gel phase, due to low fluidity of membrane lipid fatty-acyl chains, membrane proteins have restricted movement and thus are restrained in exercise of their physiological role. Plants depend critically on photosynthesis by chloroplast thylakoid membranes which are exposed cold environmental temperatures. Thylakoid membranes retain innate fluidity even at relatively low temperatures because of high degree of fatty-acyl disorder allowed by their high content of linolenic acid, 18-carbon chain with 3-double bonds. Gel-to-liquid crystalline phase transition temperature of biological membranes can be determined by many techniques including calorimetry, fluorescence, spin label electron paramagnetic resonance and NMR by recording measurements of the concerned parameter by at series of sample temperatures. A simple method for its determination from 13-C NMR line intensities has also been proposed.

In biological membranes, gel to liquid crystalline phase transitions play a critical role in physiological functioning of biomembranes. In gel phase, due to low fluidity of membrane lipid fatty-acyl chains, membrane proteins have restricted movement and thus are restrained in exercise of their physiological role. Plants depend critically on photosynthesis by chloroplast thylakoid membranes which are exposed cold environmental temperatures. Thylakoid membranes retain innate fluidity even at relatively low temperatures because of high degree of fatty-acyl disorder allowed by their high content of linolenic acid, 18-carbon chain with 3-double bonds. Gel-to-liquid crystalline phase transition temperature of biological membranes can be determined by many techniques including calorimetry, fluorescence, spin label electron paramagnetic resonance and NMR by recording measurements of the concerned parameter by at series of sample temperatures. A simple method for its determination from 13-C NMR line intensities has also been proposed.

在 生物膜biological membranes中，从凝胶gel到液晶的相变是其维持生理机能的关键。在凝胶相中，由于膜脂质脂肪酰基链membrane lipid fatty-acyl chains的流动性低，膜蛋白membrane proteins的运动受到限制，因此其生理机能的发挥受到限制。植物非常依赖暴露于低温环境下叶绿体类囊体膜chloroplast thylakoid membranes的光合作用photosynthesis。由于其高含量的亚麻酸linolenic acid——带有3个双键的18碳链允许高度的脂肪酰基紊乱，类囊体膜即使在相对较低的温度下也能保持固有的流动性。运用众多技术，包括量热法calorimetry，荧光法fluorescence，自旋标记电子顺磁共振spin label electron paramagnetic resonance和NMR，通过记录各种实验温度下有关参数的测量值来确定生物膜凝胶到液晶相变的温度。人们还提出了一种用13-C NMR谱线强度来测定的简单方法。


It has been proposed that some biological systems might lie near critical points. Examples include neural networks in the salamander retina, bird flocks gene expression networks in Drosophila, and protein folding. However, it is not clear whether or not alternative reasons could explain some of the phenomena supporting arguments for criticality. It has also been suggested that biological organisms share two key properties of phase transitions: the change of macroscopic behavior and the coherence of a system at a critical point.

It has been proposed that some biological systems might lie near critical points. Examples include neural networks in the salamander retina, bird flocks gene expression networks in Drosophila, and protein folding. However, it is not clear whether or not alternative reasons could explain some of the phenomena supporting arguments for criticality. It has also been suggested that biological organisms share two key properties of phase transitions: the change of macroscopic behavior and the coherence of a system at a critical point.

曾经有观点认为生物系统可能位于临界点附近。例如蝾螈视网膜中的神经网络，果蝇中的鸟群基因表达网络和蛋白质折叠protein folding。但是，尚不清楚替代原因是否可以解释某些现象来支持关键性论证。另一个观点认为，生物有机体具有两个重要的相变特性：宏观行为的变化和系统在临界点的一致性。


The characteristic feature of second order phase transitions is the appearance of fractals in some scale-free properties. It has long been known that protein globules are shaped by interactions with water. There are 20 amino acids that form side groups on protein peptide chains range from hydrophilic to hydrophobic, causing the former to lie near the globular surface, while the latter lie closer to the globular center. Twenty fractals were discovered in solvent associated surface areas of > 5000 protein segments [39]. The existence of these fractals proves that proteins function near critical points of second-order phase transitions.

The characteristic feature of second order phase transitions is the appearance of fractals in some scale-free properties. It has long been known that protein globules are shaped by interactions with water. There are 20 amino acids that form side groups on protein peptide chains range from hydrophilic to hydrophilic, causing the former to lie near the globular surface, while the latter lie closer to the globular center. Twenty fractals were discovered in solvent associated surface areas of > 5000 protein segments [39]. The existence of these fractals proves that proteins function near critical points of second-order phase transitions.

二阶相变的特征是在某些无标度特性scale-free properties中出现了分形fractals。众所周知，蛋白质球是通过与水的相互作用形成的。蛋白质肽链protein peptide chains上形成侧基的氨基酸amino acids有20种（从亲水性hydrophilic到疏水性hydrophilic都有）使亲水性的氨基酸位于球状表面附近，疏水性的氨基酸更靠近球状中心。实验人员在一个在与溶剂相关的且表面积大于5000个蛋白质片段的区域中发现了二十个分形。这些分形的存在证明了蛋白质在二阶相变的临界点附近起作用。


In groups of organisms in stress (when approaching critical transitions), correlations tend to increase, while at the same time, fluctuations also increase. This effect is supported by many experiments and observations of groups of people, mice, trees, and grassy plants.

In groups of organisms in stress (when approaching critical transitions), correlations tend to increase, while at the same time, fluctuations also increase. This effect is supported by many experiments and observations of groups of people, mice, trees, and grassy plants.

在处于压力下的生物群中（接近临界转变时），相关性会增强，波动也会增加。许多以人、小鼠、树木和草类植物为研究对象的实验都得出了支持性的结果。


Experimental 实验性

A variety of methods are applied for studying the various effects. Selected examples are: A variety of methods are applied for studying the various effects. Selected examples are: 研究各种效果的方法多种多样。部分示例如下：

  • 热重量分析法（非常常见）Thermogravimetry
  • X射线衍射法X-ray diffraction
  • 中子衍射Neutron diffraction
  • 拉曼光谱法Raman Spectroscopy
  • SQUID（磁跃迁测量）
  • 霍尔效应Hall effect（磁跃迁测量）
  • 穆斯堡尔光谱法Mössbauer spectroscopy（同时测量磁性和非磁性跃迁。限制在大约800–1000°C的温度下）
  • 扰动角关联Perturbed angular correlation（同时测量磁性和非磁性跃迁。没有温度限制。已经执行了超过2000°C的操作，理论上可能达到最高晶体材料，例如钽碳化carbide 4215°C。）

See also 其他参考资料

  • 同素异形体Allotropy
  • 自动催化反应和序生成Autocatalytic reactions and order creation
  • 晶体生长Crystal growth
    • 谷物异常生长Abnormal grain growth
  • 差示扫描量热法Differential scanning calorimetry
  • 无扩散相变Diffusionless transformations
  • 埃伦费斯特方程Ehrenfest equations
  • 阻塞（物理）Jamming (physics)
  • 开尔文探针力显微镜Kelvin probe force microscope
  • 朗道二阶相变理论Landau theory of second order phase transition
  • 激光加热基座法Laser-heated pedestal growth
  • 物质状态列表List of states of matter
  • 微下拉法Micro-pulling-down
  • 渗流理论Percolation theory
    • 连续介质渗流理论Continuum percolation theory
  • 超流体膜Superfluid film
  • 超辐射相变Superradiant phase transition
  • 拓扑量子场论Topological quantum field theory

References 参考文献

Further reading 扩展阅读

  • Fisher, M.E. (1974). "The renormalization group in the theory of critical behavior". Rev. Mod. Phys. 46 (4): 597–616. Bibcode:1974RvMP...46..597F. doi:10.1103/revmodphys.46.597.
  • Goldenfeld, N., Lectures on Phase Transitions and the Renormalization Group, Perseus Publishing (1992).
  • M.R.Khoshbin-e-Khoshnazar, Ice Phase Transition as a sample of finite system phase transition, (Physics Education(India)Volume 32. No. 2, Apr - Jun 2016)[1]
取自“https://wiki.swarma.org/index.php?title=相变&oldid=21533”