网络中心性
此词条暂由水流心不竞初译,未经审校,带来阅读不便,请见谅。已由Bai审校。
| Network science | ||||
|---|---|---|---|---|
| 模板:CSS image crop | ||||
| 模板:Hlist | ||||
| Network types | ||||
| Graphs | ||||
|
||||
| 模板:Hlist | ||||
| Models | ||||
|
||||
| 模板:Hlist | ||||
In graph theory and network analysis, indicators of centrality identify the most important vertices within a graph. Applications include identifying the most influential person(s) in a social network, key infrastructure nodes in the Internet or urban networks, and super-spreaders of disease. Centrality concepts were first developed in social network analysis, and many of the terms used to measure centrality reflect their sociological origin.[1]
In graph theory and network analysis, indicators of centrality identify the most important vertices within a graph. Applications include identifying the most influential person(s) in a social network, key infrastructure nodes in the Internet or urban networks, and super-spreaders of disease. Centrality concepts were first developed in , and many of the terms used to measure centrality reflect their sociological origin.
They should not be confused with node influence metrics, which seek to quantify the influence of every node in the network.
They should not be confused with node influence metrics, which seek to quantify the influence of every node in the network.
在图论 graph theory 和网络分析 network analysis 中,中心性 centrality 指标用于识别图中最重要的顶点。其应用包括在社交网络中识别出最有影响力的个人,在因特网或城市网络中识别出最为关键的基础设施节点,以及识别疾病的超级传播者。中心性的概念最初是在社交网络分析 social network analysis中发展起来的,许多用于衡量中心性的术语都反映出了它们的社会学起源。[1]中心性不应与节点影响度相混淆,后者意在量化网络中每个节点的影响。
中心性指数的定义与特性Definition and characterization of centrality indices
Centrality indices are answers to the question "What characterizes an important vertex?" The answer is given in terms of a real-valued function on the vertices of a graph, where the values produced are expected to provide a ranking which identifies the most important nodes.[2][3][4]
Centrality indices are answers to the question "What characterizes an important vertex?" The answer is given in terms of a real-valued function on the vertices of a graph, where the values produced are expected to provide a ranking which identifies the most important nodes.
中心性指数 centrality indices是对“重要顶点的特征是什么?”这一问题的回答。这个回答是以图中顶点的实值函数的形式给出的,可根据产生的函数值排序以确定最为重要的节点。[2][3][4]
The word "importance" has a wide number of meanings, leading to many different definitions of centrality. Two categorization schemes have been proposed.
The word "importance" has a wide number of meanings, leading to many different definitions of centrality. Two categorization schemes have been proposed.
“重要性”的含义十分广泛,因此导致了许多不同的中心性定义方式,我们可以将各种不同的定义方式划分为如下两类。
"Importance" can be conceived in relation to a type of flow or transfer across the network. This allows centralities to be classified by the type of flow they consider important.[3] "Importance" can alternatively be conceived as involvement in the cohesiveness of the network. This allows centralities to be classified based on how they measure cohesiveness.[5] Both of these approaches divide centralities in distinct categories. A further conclusion is that a centrality which is appropriate for one category will often "get it wrong" when applied to a different category.[3]
"Importance" can be conceived in relation to a type of flow or transfer across the network. This allows centralities to be classified by the type of flow they consider important. "Importance" can alternatively be conceived as involvement in the cohesiveness of the network. This allows centralities to be classified based on how they measure cohesiveness.Both of these approaches divide centralities in distinct categories. A further conclusion is that a centrality which is appropriate for one category will often "get it wrong" when applied to a different category.
“重要性”可以被设想为与网络中的某种流动或传输有关。这允许根据重要的流动的类型对中心性进行分类。[3] “重要性”也可以被设想为与网络的内聚力 cohesiveness有关。这允许根据内聚力的度量方式对中心性进行分类。[5]这两种方法在不同类别中划分了中心性。进一步的结论是,适用于某一类别的中心性在应用于另一类别时往往会“出错”。[3]
When centralities are categorized by their approach to cohesiveness, it becomes apparent that the majority of centralities inhabit one category. The count of the number of walks starting from a given vertex differs only in how walks are defined and counted. Restricting consideration to this group allows for a soft characterization which places centralities on a spectrum from walks of length one (degree centrality) to infinite walks (eigenvalue centrality).[2][6] The observation that many centralities share this familial relationships perhaps explains the high rank correlations between these indices.
When centralities are categorized by their approach to cohesiveness, it becomes apparent that the majority of centralities inhabit one category. The count of the number of walks starting from a given vertex differs only in how walks are defined and counted. Restricting consideration to this group allows for a soft characterization which places centralities on a spectrum from walks of length one (degree centrality) to infinite walks (eigenvalue centrality). The observation that many centralities share this familial relationships perhaps explains the high rank correlations between these indices.
当根据内聚力方法对中心性进行分类时,很明显大多数中心性都将被划分于同一类别。起始于给定顶点的步数总和仅取决于步数的定义以及计数方式。这种分类方式的不足表现为它仅能较弱的描绘中心性特征,即按照一步步长(度中心性 degree centrality)到无穷步步长(特征向量中心性 eigenvalue centrality)的方式将中心性置于一种光谱状的分类中。[2][6]观察到许多中心性共享这种家庭关系,这或许能解释这些指数之间的高阶相关性。
网络流特征Characterization by network flows
A network can be considered a description of the paths along which something flows. This allows a characterization based on the type of flow and the type of path encoded by the centrality. A flow can be based on transfers, where each indivisible item goes from one node to another, like a package delivery going from the delivery site to the client's house. A second case is serial duplication, in which an item is replicated so that both the source and the target have it. An example is the propagation of information through gossip, with the information being propagated in a private way and with both the source and the target nodes being informed at the end of the process. The last case is parallel duplication, with the item being duplicated to several links at the same time, like a radio broadcast which provides the same information to many listeners at once.[3]
A network can be considered a description of the paths along which something flows. This allows a characterization based on the type of flow and the type of path encoded by the centrality. A flow can be based on transfers, where each indivisible item goes from one node to another, like a package delivery going from the delivery site to the client's house. A second case is serial duplication, in which an item is replicated so that both the source and the target have it. An example is the propagation of information through gossip, with the information being propagated in a private way and with both the source and the target nodes being informed at the end of the process. The last case is parallel duplication, with the item being duplicated to several links at the same time, like a radio broadcast which provides the same information to many listeners at oe.
一个网络可以被看成是对某种物体流动的路径描述。这允许基于流动的类型和由中心性编码的路径类型进行表征。流可以基于传输,即每个不可分割的项目从一个节点到另一个节点,就像一个包裹从配送站传递到客户的房子。第二种情况是串行复制,在这种情况下,一个项目被复制以便源头和目标节点都拥有它。例如通过流言传播信息,信息以私有方式传播,并在流程结束时通知源节点和目标节点。最后一种情况是并行复制,即项目同时被复制到几个链接,就像无线电广播一次性向多个听众提供相同的信息。[3]
Likewise, the type of path can be constrained to geodesics (shortest paths), paths (no vertex is visited more than once), trails (vertices can be visited multiple times, no edge is traversed more than once), or walks (vertices and edges can be visited/traversed multiple times).[3]
Likewise, the type of path can be constrained to geodesics (shortest paths), paths (no vertex is visited more than once), trails (vertices can be visited multiple times, no edge is traversed more than once), or walks (vertices and edges can be visited/traversed multiple times).
同样,路径类型可以被限定为 测地线geodesics (最短路径)、路径(对顶点的访问不超过一次)、小径(可以访问多次顶点,没有边被访问超过一次)或者步子(可以多次访问/穿过多次顶点和边)。
行走结构特征Characterization by walk structure
An alternative classification can be derived from how the centrality is constructed. This again splits into two classes. Centralities are either radial or medial. Radial centralities count walks which start/end from the given vertex. The degree and eigenvalue centralities are examples of radial centralities, counting the number of walks of length one or length infinity. Medial centralities count walks which pass through the given vertex. The canonical example is Freeman's betweenness centrality, the number of shortest paths which pass through the given vertex.[5]
An alternative classification can be derived from how the centrality is constructed. This again splits into two classes. Centralities are either radial or medial. Radial centralities count walks which start/end from the given vertex. The degree and eigenvalue centralities are examples of radial centralities, counting the number of walks of length one or length infinity. Medial centralities count walks which pass through the given vertex. The canonical example is Freeman's betweenness centrality, the number of shortest paths which pass through the given vertex.
可以从中心性的构造方式推导出另一种分类方法。这又分成了两个类。中心性可以是径向的,也可以是中间的。径向中心性计算从给定顶点开始/结束的步数。度中心性和特征向量中心性是 径向中心性Radial centralities的例子,计算长度为一或无穷大的步数。 中间中心性Medial centralities计算通过给定顶点的步数。典型的例子是弗里曼 Freeman的 中介中心性Betweenness centrality,,即通过给定顶点的最短路径的数量。[5]
Likewise, the counting can capture either the volume or the length of walks. Volume is the total number of walks of the given type. The three examples from the previous paragraph fall into this category. Length captures the distance from the given vertex to the remaining vertices in the graph. Freeman's closeness centrality, the total geodesic distance from a given vertex to all other vertices, is the best known example.[5] Note that this classification is independent of the type of walk counted (i.e. walk, trail, path, geodesic).
Likewise, the counting can capture either the volume or the length of walks. Volume is the total number of walks of the given type. The three examples from the previous paragraph fall into this category. Length captures the distance from the given vertex to the remaining vertices in the graph. Freeman's closeness centrality, the total geodesic distance from a given vertex to all other vertices, is the best known example. Note that this classification is independent of the type of walk counted (i.e. walk, trail, path, geodesic).
同样地,计数可以记录行走的数量或长度。量是给定类型的总步数。上一段的三个例子就属于这一类。长度则给出从给定顶点到图中其余顶点的距离。Freeman的 接近中心性Closeness centrality,即从一个给定顶点到所有其他顶点的总测地线距离,是最著名的例子。[5]请注意,这种分类独立于步行计数的类型(即:步行,小道,路径,测地线)。
Borgatti and Everett propose that this typology provides insight into how best to compare centrality measures. Centralities placed in the same box in this 2×2 classification are similar enough to make plausible alternatives; one can reasonably compare which is better for a given application. Measures from different boxes, however, are categorically distinct. Any evaluation of relative fitness can only occur within the context of predetermining which category is more applicable, rendering the comparison moot.[5]
Borgatti and Everett propose that this typology provides insight into how best to compare centrality measures. Centralities placed in the same box in this 2×2 classification are similar enough to make plausible alternatives; one can reasonably compare which is better for a given application. Measures from different boxes, however, are categorically distinct. Any evaluation of relative fitness can only occur within the context of predetermining which category is more applicable, rendering the comparison moot.
博尔加蒂 Borgatti和埃弗雷特 Everett提出,这种类型为如何最好地比较中心性度量提供了见解。在这个2×2分类中,放在同一盒子中的中心性足够相似,可以做出合理的选择; 人们可以合理地比较哪个对于给定的应用更好。然而,不同盒子中的度量方法是截然不同的。只有在预先确定哪个类别更适用的情况下,对相对适应性的评估才会发生,这使得比较变得毫无意义。[5]
光谱上存在的径向量中心Radial-volume centralities exist on a spectrum
The characterization by walk structure shows that almost all centralities in wide use are radial-volume measures. These encode the belief that a vertex's centrality is a function of the centrality of the vertices it is associated with. Centralities distinguish themselves on how association is defined.
The characterization by walk structure shows that almost all centralities in wide use are radial-volume measures. These encode the belief that a vertex's centrality is a function of the centrality of the vertices it is associated with. Centralities distinguish themselves on how association is defined.
步行结构的特征表明,几乎所有广泛使用的中心性都是径向量的衡量。这得出结论顶点的中心性是与之相关联的顶点中心性的函数。中心性根据如何定义关联而不同。
Bonacich showed that if association is defined in terms of walks, then a family of centralities can be defined based on the length of walk considered.[2] Degree centrality counts walks of length one, while eigenvalue centrality counts walks of length infinity. Alternative definitions of association are also reasonable. Alpha centrality allows vertices to have an external source of influence. Estrada's subgraph centrality proposes only counting closed paths (triangles, squares, etc.).
Bonacich showed that if association is defined in terms of walks, then a family of centralities can be defined based on the length of walk considered. Degree centrality counts walks of length one, while eigenvalue centrality counts walks of length infinity. Alternative definitions of association are also reasonable. Alpha centrality allows vertices to have an external source of influence. Estrada's subgraph centrality proposes only counting closed paths (triangles, squares, etc.).
博纳奇 Bonacich指出,如果联想是根据行走来定义的,那么可以根据考虑的行走长度来定义一个中心性家族。[2]度中心性计算长度为1的行走,特征向量中心性计算长度为无穷大的行走。关联的其他定义也是合理的。 阿尔法中心性Alpha centrality允许顶点有一个外部影响源。埃斯特拉达 Estrada的 子图中心性Subgraph centrality 提出只计算封闭路径(三角形、正方形等)。).
The heart of such measures is the observation that powers of the graph's adjacency matrix gives the number of walks of length given by that power. Similarly, the matrix exponential is also closely related to the number of walks of a given length. An initial transformation of the adjacency matrix allows a different definition of the type of walk counted. Under either approach, the centrality of a vertex can be expressed as an infinite sum, either
The heart of such measures is the observation that powers of the graph's adjacency matrix gives the number of walks of length given by that power. Similarly, the matrix exponential is also closely related to the number of walks of a given length. An initial transformation of the adjacency matrix allows a different definition of the type of walk counted. Under either approach, the centrality of a vertex can be expressed as an infinite sum, either
这些度量方法的核心是这种现象:图中 邻接矩阵 adjacency matrix 的幂给出了由该幂给出的步长的数目。同样, 矩阵指数Matrix exponential也与给定步长的数目密切相关。邻接矩阵的初始转换允许对步行计数的类型进行不同的定义。无论采用哪种方法,顶点的中心性都可以表示为无穷和
- [math]\displaystyle{ \sum_{k=0}^\infty A_{R}^{k} \beta^k }[/math]
[math]\displaystyle{ \sum_{k=0}^\infty A_{R}^{k} \beta^k }[/math]
< math > sum _ { k = 0} ^ infty a _ { r } ^ { k } beta ^ k </math >
for matrix powers or
for matrix powers or
矩阵幂或者
- [math]\displaystyle{ \sum_{k=0}^\infty \frac{(A_R \beta)^k}{k!} }[/math]
[math]\displaystyle{ \sum_{k=0}^\infty \frac{(A_R \beta)^k}{k!} }[/math]
< math > sum { k = 0} ^ infty frac {(a _ r beta) ^ k }{ k!{/math >
for matrix exponentials, where
for matrix exponentials, where
矩阵指数,其中
- [math]\displaystyle{ k }[/math] is walk length,
- [math]\displaystyle{ A_R }[/math] is the transformed adjacency matrix, and
- [math]\displaystyle{ \beta }[/math] is a discount parameter which ensures convergence of the sum.
K为步长,A_R是邻接矩阵的转秩,\beta是保证收敛的折扣参数。
Bonacich's family of measures does not transform the adjacency matrix. Alpha centrality replaces the adjacency matrix with its resolvent. Subgraph centrality replaces the adjacency matrix with its trace. A startling conclusion is that regardless of the initial transformation of the adjacency matrix, all such approaches have common limiting behavior. As [math]\displaystyle{ \beta }[/math] approaches zero, the indices converge to degree centrality. As [math]\displaystyle{ \beta }[/math] approaches its maximal value, the indices converge to eigenvalue centrality.[6]
Bonacich's family of measures does not transform the adjacency matrix. Alpha centrality replaces the adjacency matrix with its resolvent. Subgraph centrality replaces the adjacency matrix with its trace. A startling conclusion is that regardless of the initial transformation of the adjacency matrix, all such approaches have common limiting behavior. As [math]\displaystyle{ \beta }[/math] approaches zero, the indices converge to degree centrality. As [math]\displaystyle{ \beta }[/math] approaches its maximal value, the indices converge to eigenvalue centrality.
Bonacich的一系列度量并没有改变邻接矩阵。阿尔法中心性用它的解决方案替代了邻接矩阵。子图中心性用它的踪迹取代了邻接矩阵。一个令人吃惊的结论是,不管邻接矩阵最初的转变是什么,所有这些方法都有共同的限制行为。随着贝塔系数趋近于零,指数收敛到度中心性。随着贝塔系数接近其最大值,指数收敛到特征向量中心性。[6]
博弈论中心性Game-theoretic centrality
The common feature of most of the aforementioned standard measures is that they assess the importance of a node by focusing only on the role that a node plays by itself. However, in many applications such an approach is inadequate because of synergies that may occur
The common feature of most of the aforementioned standard measures is that they assess the importance of a node by focusing only on the role that a node plays by itself. However, in many applications such an approach is inadequate because of synergies that may occur
上述大多数标准度量的共同特点是,它们通过只关注一个节点本身所扮演的角色来评估确定节点的重要性。然而, 在许多应用中,这种方法是不充分的,因为可能会发生协同作用
if the functioning of nodes is considered in groups.
if the functioning of nodes is considered in groups.
如果将节点的功能分组考虑。
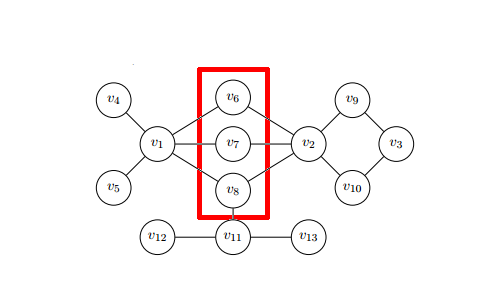
Example of game-theoretic centrality
博弈论中心性 Game-theoretic centrality的例子
For example, consider the problem of stopping an epidemic. Looking at above image of network, which nodes should we vaccinate? Based on previously described measures, we want to recognize nodes that are the most important in disease spreading. Approaches based only on centralities, that focus on individual features of nodes, may not be good idea. Nodes in the red square, individually cannot stop disease spreading, but considering them as a group, we clearly see that they can stop disease if it has started in nodes [math]\displaystyle{ v_1 }[/math], [math]\displaystyle{ v_4 }[/math], and [math]\displaystyle{ v_5 }[/math]. Game-theoretic centralities try to consult described problems and opportunities, using tools from game-theory. The approach proposed in [7] uses the Shapley value. Because of the time-complexity hardness of the Shapley value calculation, most efforts in this domain are driven into implementing new algorithms and methods which rely on a peculiar topology of the network or a special character of the problem. Such an approach may lead to reducing time-complexity from exponential to polynomial.
For example, consider the problem of stopping an epidemic. Looking at above image of network, which nodes should we vaccinate? Based on previously described measures, we want to recognize nodes that are the most important in disease spreading. Approaches based only on centralities, that focus on individual features of nodes, may not be good idea. Nodes in the red square, individually cannot stop disease spreading, but considering them as a group, we clearly see that they can stop disease if it has started in nodes [math]\displaystyle{ v_1 }[/math], [math]\displaystyle{ v_4 }[/math], and [math]\displaystyle{ v_5 }[/math]. Game-theoretic centralities try to consult described problems and opportunities, using tools from game-theory. The approach proposed in uses the Shapley value. Because of the time-complexity hardness of the Shapley value calculation, most efforts in this domain are driven into implementing new algorithms and methods which rely on a peculiar topology of the network or a special character of the problem. Such an approach may lead to reducing time-complexity from exponential to polynomial.
例如,考虑阻止流行病的问题。看看上面的网络图像,我们应该给哪些节点接种疫苗?基于前面描述的度量,我们希望识别在疾病传播中最重要的节点。仅仅基于中心性的方法,即关注节点的个别特性,可能不是一个好主意。红色方块中的节点,单独不能阻止疾病的传播,但把它们作为一个群体来考虑,我们清楚地看到,如果疾病在节点 < math > v _ 1 </math > 、 < math > v _ 4 </math > 和 < math > v _ 5 </math > 中开始,它们就能阻止疾病的传播。博弈论中心性试图利用博弈论中的工具来研究所描述的问题和机会。本文提出的方法[8]使用了 Shapley 值。由于 Shapley 值计算的时间复杂性,这一领域的大部分工作都集中在实现新的算法和方法,这些算法和方法依赖于网络的特殊拓扑结构或问题的特殊性质。这种方法可以将时间复杂度从指数级降低到多项式级。
Similarly, the solution concept authority distribution ([9]) applies the Shapley-Shubik power index, rather than the Shapley value, to measure the bilateral direct influence between the players. The distribution is indeed a type of engenvector centrality. It is used to sort big data objects in Hu (2020)[10], such as ranking U.S. colleges.
Similarly, the solution concept authority distribution () applies the Shapley-Shubik power index, rather than the Shapley value, to measure the bilateral direct influence between the players. The distribution is indeed a type of engenvector centrality. It is used to sort big data objects in Hu (2020), such as ranking U.S. colleges.
同样,权限分配的解决方案()[11]采用 Shapley-Shubik 幂指数,而不是 Shapley 值来衡量参与者之间的双边直接影响。这种分布确实是一种产生特征向量中心性的类型。它用于对 Hu (2020)中的大数据对象进行排序[12],比如美国大学排名。
重要限制Important limitations
Centrality indices have two important limitations, one obvious and the other subtle. The obvious limitation is that a centrality which is optimal for one application is often sub-optimal for a different application. Indeed, if this were not so, we would not need so many different centralities. An illustration of this phenomenon is provided by the Krackhardt kite graph, for which three different notions of centrality give three different choices of the most central vertex.[13]
Centrality indices have two important limitations, one obvious and the other subtle. The obvious limitation is that a centrality which is optimal for one application is often sub-optimal for a different application. Indeed, if this were not so, we would not need so many different centralities. An illustration of this phenomenon is provided by the Krackhardt kite graph, for which three different notions of centrality give three different choices of the most central vertex.
中心性指标有两个重要的局限性,一个显而易见,另一个则不易察觉。显而易见的局限性是,对于一个应用最优的中心性对于另一个应用常常是次优的。事实上,如果不是这样,我们就不需要这么多不同的中心性。克拉克哈特风筝图为这一现象提供了一个例证,对于这个图,三个不同的中心性概念给出了最中心顶点的三种不同选择。[14]
The more subtle limitation is the commonly held fallacy that vertex centrality indicates the relative importance of vertices. Centrality indices are explicitly designed to produce a ranking which allows indication of the most important vertices.[2][3] This they do well, under the limitation just noted. They are not designed to measure the influence of nodes in general. Recently, network physicists have begun developing node influence metrics to address this problem.
The more subtle limitation is the commonly held fallacy that vertex centrality indicates the relative importance of vertices. Centrality indices are explicitly designed to produce a ranking which allows indication of the most important vertices. This they do well, under the limitation just noted. They are not designed to measure the influence of nodes in general. Recently, network physicists have begun developing node influence metrics to address this problem.
更不易察觉的限制是通常会错误地认为顶点中心性表示顶点的相对重要性。中心性指数被明确地设计来产生一个指出最重要顶点的排名。[2][3]在刚才提到的限制下,他们做得很好。它们通常不用来度量节点的影响力。最近,网络物理学家已经开始开发节点影响力度量Node influence metrics 来解决这个问题。
The error is two-fold. Firstly, a ranking only orders vertices by importance, it does not quantify the difference in importance between different levels of the ranking. This may be mitigated by applying Freeman centralization to the centrality measure in question, which provide some insight to the importance of nodes depending on the differences of their centralization scores. Furthermore, Freeman centralization enables one to compare several networks by comparing their highest centralization scores.[15] This approach, however, is seldom seen in practice.[citation needed]
The error is two-fold. Firstly, a ranking only orders vertices by importance, it does not quantify the difference in importance between different levels of the ranking. This may be mitigated by applying Freeman centralization to the centrality measure in question, which provide some insight to the importance of nodes depending on the differences of their centralization scores. Furthermore, Freeman centralization enables one to compare several networks by comparing their highest centralization scores. This approach, however, is seldom seen in practice.
错误有两方面。首先,一个排名只根据顶点的重要性排序,它并不对节点重要性的不同水平进行量化区分。这可以通过将 弗里曼中心度Freeman centralization应用到中心性度量来缓解,这可以根据节点的中心度得分差异对节点的重要性提供一些见解。此外,弗里曼中心度使人们能够通过比较几个网络的最高中心度得分来比较它们。[15]然而,这种方法在实践中很少见到。[citation needed]
Secondly, the features which (correctly) identify the most important vertices in a given network/application do not necessarily generalize to the remaining vertices.
Secondly, the features which (correctly) identify the most important vertices in a given network/application do not necessarily generalize to the remaining vertices.
其次,用以(正确地)识别给定网络/应用中最重要顶点的特征并不一定适用于其余顶点。
For the majority of other network nodes the rankings may be meaningless.[16][17][18][19] This explains why, for example, only the first few results of a Google image search appear in a reasonable order. The pagerank is a highly unstable measure, showing frequent rank reversals after small adjustments of the jump parameter.[20]
For the majority of other network nodes the rankings may be meaningless. This explains why, for example, only the first few results of a Google image search appear in a reasonable order. The pagerank is a highly unstable measure, showing frequent rank reversals after small adjustments of the jump parameter.
对于大多数其他网络节点,排名可能是没有意义的。[16][17][18][19]这就解释了为什么,例如,谷歌图片搜索只有前几个结果以合理的顺序出现。网页排名是一个非常不稳定的度量,在对跳转参数进行小的调整之后显示了频繁的秩逆转。[20]
While the failure of centrality indices to generalize to the rest of the network may at first seem counter-intuitive, it follows directly from the above definitions.
While the failure of centrality indices to generalize to the rest of the network may at first seem counter-intuitive, it follows directly from the above definitions.
虽然中心性指数未能推广到网络的其他部分,乍看起来似乎是违反直觉的,但它直接遵循上述定义。
Complex networks have heterogeneous topology. To the extent that the optimal measure depends on the network structure of the most important vertices, a measure which is optimal for such vertices is sub-optimal for the remainder of the network.[16]
Complex networks have heterogeneous topology. To the extent that the optimal measure depends on the network structure of the most important vertices, a measure which is optimal for such vertices is sub-optimal for the remainder of the network.
复杂网络具有异构的拓扑结构。如果最佳度量取决于最重要顶点的网络结构,对于这些顶点最优的度量对于网络的其余部分是次优的。
Degree centrality
度中心性Degree centrality
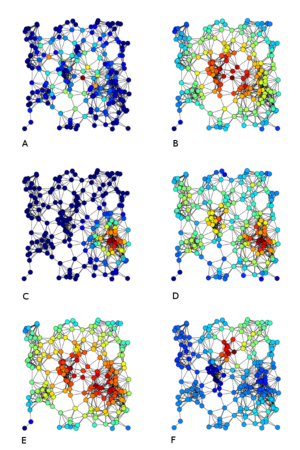
同一幅图中的实例A中介中心性,B紧密中心性,C特征向量中心性,D度中心性,E调和中心性,F卡兹中心性 Katz centrality
Historically first and conceptually simplest is degree centrality, which is defined as the number of links incident upon a node (i.e., the number of ties that a node has). The degree can be interpreted in terms of the immediate risk of a node for catching whatever is flowing through the network (such as a virus, or some information). In the case of a directed network (where ties have direction), we usually define two separate measures of degree centrality, namely indegree and outdegree. Accordingly, indegree is a count of the number of ties directed to the node and outdegree is the number of ties that the node directs to others. When ties are associated to some positive aspects such as friendship or collaboration, indegree is often interpreted as a form of popularity, and outdegree as gregariousness.
Historically first and conceptually simplest is degree centrality, which is defined as the number of links incident upon a node (i.e., the number of ties that a node has). The degree can be interpreted in terms of the immediate risk of a node for catching whatever is flowing through the network (such as a virus, or some information). In the case of a directed network (where ties have direction), we usually define two separate measures of degree centrality, namely indegree and outdegree. Accordingly, indegree is a count of the number of ties directed to the node and outdegree is the number of ties that the node directs to others. When ties are associated to some positive aspects such as friendship or collaboration, indegree is often interpreted as a form of popularity, and outdegree as gregariousness.
历史上第一个并且概念上最简单是度中心性,它定义为一个节点上事件的链接数量(即一个节点拥有的关系数量)。度可以解释为节点捕获的任何流经网络的东西(例如病毒或某些信息)的直接风险。在有向网络的情况下(关系有方向) ,我们通常定义两个独立的度中心性的度量,即 入度Indegree和 出度 Outdegree。因此,入度是指向该节点的关系数,出度是该节点指向其他节点的关系数。当关系与一些积极的方面如友谊或合作有关时,入度通常被解释为一种受欢迎的形式,而出度则被解释为一种合群的形式。
The degree centrality of a vertex [math]\displaystyle{ v }[/math], for a given graph [math]\displaystyle{ G:=(V,E) }[/math] with [math]\displaystyle{ |V| }[/math] vertices and [math]\displaystyle{ |E| }[/math] edges, is defined as
The degree centrality of a vertex [math]\displaystyle{ v }[/math], for a given graph [math]\displaystyle{ G:=(V,E) }[/math] with [math]\displaystyle{ |V| }[/math] vertices and [math]\displaystyle{ |E| }[/math] edges, is defined as
对于给定的图 g: = (v,e) </math > 与 < math > | v | </math > 顶点和 < math > | e | </math > 边,顶点的度中心性定义为
- [math]\displaystyle{ C_D(v)= \deg(v) }[/math]
[math]\displaystyle{ C_D(v)= \deg(v) }[/math]
[math]\displaystyle{ C_D(v)= \deg(v) }[/math]
Calculating degree centrality for all the nodes in a graph takes [math]\displaystyle{ \Theta(V^2) }[/math] in a dense adjacency matrix representation of the graph, and for edges takes [math]\displaystyle{ \Theta(E) }[/math] in a sparse matrix representation.
Calculating degree centrality for all the nodes in a graph takes [math]\displaystyle{ \Theta(V^2) }[/math] in a dense adjacency matrix representation of the graph, and for edges takes [math]\displaystyle{ \Theta(E) }[/math] in a sparse matrix representation.
计算一个图中所有节点的度中心性,在图的密集邻接矩阵表示中采用 Theta (v ^ 2) </math > ,在边的稀疏矩阵表示中采用Theta (e) </math > 。
The definition of centrality on the node level can be extended to the whole graph, in which case we are speaking of graph centralization.[21] Let [math]\displaystyle{ v* }[/math] be the node with highest degree centrality in [math]\displaystyle{ G }[/math]. Let [math]\displaystyle{ X:=(Y,Z) }[/math] be the [math]\displaystyle{ |Y| }[/math]-node connected graph that maximizes the following quantity (with [math]\displaystyle{ y* }[/math] being the node with highest degree centrality in [math]\displaystyle{ X }[/math]):
The definition of centrality on the node level can be extended to the whole graph, in which case we are speaking of graph centralization. Let [math]\displaystyle{ v* }[/math] be the node with highest degree centrality in [math]\displaystyle{ G }[/math]. Let [math]\displaystyle{ X:=(Y,Z) }[/math] be the [math]\displaystyle{ |Y| }[/math]-node connected graph that maximizes the following quantity (with [math]\displaystyle{ y* }[/math] being the node with highest degree centrality in [math]\displaystyle{ X }[/math]):
节点级中心性的定义可以扩展到整个图,在这种情况下,我们指的是图的中心度。[22]设 < math > v </math > 为 < math > g </math > 中度中心性最高的节点。让 < math > x: = (y,z) </math > 是 < math > | y | </math > 节点连接图,最大化下列数量(< math > y * </math > 是 < math > 中度最高的节点) :
- [math]\displaystyle{ H= \sum^{|Y|}_{j=1} [C_D(y*)-C_D(y_j)] }[/math]
[math]\displaystyle{ H= \sum^{|Y|}_{j=1} [C_D(y*)-C_D(y_j)] }[/math]
< math > h = sum ^ { | y | }{ j = 1}[ c _ d (y *)-c _ d (y _ j)] </math >
Correspondingly, the degree centralization of the graph [math]\displaystyle{ G }[/math] is as follows:
Correspondingly, the degree centralization of the graph [math]\displaystyle{ G }[/math] is as follows:
相应地,图形 < math > g </math > 的度中心度如下:
- [math]\displaystyle{ C_D(G)= \frac{\sum^{|V|}_{i=1} [C_D(v*)-C_D(v_i)]}{H} }[/math]
[math]\displaystyle{ C_D(G)= \frac{\sum^{|V|}_{i=1} [C_D(v*)-C_D(v_i)]}{H} }[/math]
< math > c _ d (g) = frac { sum ^ { | v | } _ { i = 1}[ c _ d (v *)-c _ d (v _ i)]}{ h } </math >
The value of [math]\displaystyle{ H }[/math] is maximized when the graph [math]\displaystyle{ X }[/math] contains one central node to which all other nodes are connected (a star graph), and in this case
The value of [math]\displaystyle{ H }[/math] is maximized when the graph [math]\displaystyle{ X }[/math] contains one central node to which all other nodes are connected (a star graph), and in this case
当图形 < math > x </math > 包含与一个所有其他节点都连接的中心节点(一个星形图)时,< math > h </math > 的值最大化,在这种情况下
- [math]\displaystyle{ H=(n-1)\cdot((n-1)-1)=n^2-3n+2. }[/math]
[math]\displaystyle{ H=(n-1)\cdot((n-1)-1)=n^2-3n+2. }[/math]
(n-1)-1) = n ^ 2-3n + 2
So, for any graph [math]\displaystyle{ G:=(V,E), }[/math]
So, for any graph [math]\displaystyle{ G:=(V,E), }[/math]
所以,对于任意的图 < math > g: = (v,e) ,</math >
- [math]\displaystyle{ C_D(G)= \frac{\sum^{|V|}_{i=1} [C_D(v*)-C_D(v_i)] }{|V|^2-3|V|+2} }[/math]
[math]\displaystyle{ C_D(G)= \frac{\sum^{|V|}_{i=1} [C_D(v*)-C_D(v_i)] }{|V|^2-3|V|+2} }[/math]
< math > c _ d (g) = frac { sum ^ { | v | } _ { i = 1}[ c _ d (v *)-c _ d (v _ i)]}{ | v | ^ 2-3 | v | + 2} </math >
Closeness centrality
紧密中心性Closeness centrality
In a connected graph, the normalized closeness centrality (or closeness) of a node is the average length of the shortest path between the node and all other nodes in the graph. Thus the more central a node is, the closer it is to all other nodes.
In a connected graph, the normalized closeness centrality (or closeness) of a node is the average length of the shortest path between the node and all other nodes in the graph. Thus the more central a node is, the closer it is to all other nodes.
在连通图中,节点的标准紧密中心性(或贴近性)是节点与图中所有其他节点之间最短路径的平均长度。因此,一个节点越是中心,它就越接近所有其他节点。
Closeness was defined by Alex Bavelas (1950) as the reciprocal of the farness,[23][24] that is:
Closeness was defined by Alex Bavelas (1950) as the reciprocal of the farness, that is:
亚历克斯 · 巴维拉斯 Alex Bavelas (1950)将贴近性定义为相对于距离的倒数,即:
- [math]\displaystyle{ C(x)= \frac{1}{\sum_y d(y,x)} }[/math]
[math]\displaystyle{ C(x)= \frac{1}{\sum_y d(y,x)} }[/math]
C (x) = frac {1}{ sum _ y d (y,x)} </math >
where [math]\displaystyle{ d(y,x) }[/math] is the distance between vertices [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math]. However, when speaking of closeness centrality, people usually refer to its normalized form, generally given by the previous formula multiplied by [math]\displaystyle{ N-1 }[/math], where [math]\displaystyle{ N }[/math] is the number of nodes in the graph. This adjustment allows comparisons between nodes of graphs of different sizes.
where [math]\displaystyle{ d(y,x) }[/math] is the distance between vertices [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math]. However, when speaking of closeness centrality, people usually refer to its normalized form, generally given by the previous formula multiplied by [math]\displaystyle{ N-1 }[/math], where [math]\displaystyle{ N }[/math] is the number of nodes in the graph. This adjustment allows comparisons between nodes of graphs of different sizes.
其中 < math > d (y,x) </math > 是顶点 < math > x </math > 和 < math > y </math > 之间的距离。然而,当谈到紧密中心性时,人们通常会提到它的标准化形式,一般是以前的公式乘以 < math > N-1 </math > ,其中 < math > n </math > 是图中的节点数。这种调整允许比较不同大小图形的节点。
Taking distances from or to all other nodes is irrelevant in undirected graphs, whereas it can produce totally different results in directed graphs (e.g. a website can have a high closeness centrality from outgoing link, but low closeness centrality from incoming links).
Taking distances from or to all other nodes is irrelevant in undirected graphs, whereas it can produce totally different results in directed graphs (e.g. a website can have a high closeness centrality from outgoing link, but low closeness centrality from incoming links).
从所有其他节点或到所有其他节点的距离在 无向图Undirected graphs中是不相关的,但是在 有向图Directed graphs中可能产生完全不同的结果(例如:一个网站可以从传出链接获得高的紧密中心性,而从传入链接获得低的紧密中心性)。
Harmonic centrality
调和中心性Harmonic centrality
In a (not necessarily connected) graph, the harmonic centrality reverses the sum and reciprocal operations in the definition of closeness centrality:
In a (not necessarily connected) graph, the harmonic centrality reverses the sum and reciprocal operations in the definition of closeness centrality:
在一个(不一定是连通的)图中,调和中心性反转了紧密中心性定义中的和互反运算:
- [math]\displaystyle{ H(x)= \sum_{y \neq x} \frac{1}{d(y,x)} }[/math]
[math]\displaystyle{ H(x)= \sum_{y \neq x} \frac{1}{d(y,x)} }[/math]
< math > h (x) = sum { y neq x } frac {1}{ d (y,x)} </math >
where [math]\displaystyle{ 1 / d(y,x) = 0 }[/math] if there is no path from [math]\displaystyle{ y }[/math] to [math]\displaystyle{ x }[/math]. Harmonic centrality can be normalized by dividing by [math]\displaystyle{ N-1 }[/math], where [math]\displaystyle{ N }[/math] is the number of nodes in the graph.
where [math]\displaystyle{ 1 / d(y,x) = 0 }[/math] if there is no path from [math]\displaystyle{ y }[/math] to [math]\displaystyle{ x }[/math]. Harmonic centrality can be normalized by dividing by [math]\displaystyle{ N-1 }[/math], where [math]\displaystyle{ N }[/math] is the number of nodes in the graph.
其中 < math > 1/d (y,x) = 0 </math > 如果没有来自< math > y </math > to < math > x </math >的路径 。调和中心性可以通过除以 < math > N-1 </math > 来标准化,其中 < math > n </math > 是图中的节点数。
Harmonic centrality was proposed by Marchiori and Latora (2000)[25] and then independently by Dekker (2005), using the name "valued centrality,"[26] and by Rochat (2009).[27]
Harmonic centrality was proposed by Marchiori and Latora (2000) and then independently by Dekker (2005), using the name "valued centrality," and by Rochat (2009).
调和中心性是由马奇奥里 Marchiori 和拉托拉 Latora (2000)提出的[25],然后由德克 Dekker (2005)以“有价值的中心性”之名独立提出的,[28]再由罗切特 Rochat提出(2009)。[29]
Betweenness centrality
中介中心性Betweenness centrality
Hue (from red = 0 to blue = max) shows the node betweenness.
色调(从红色 = 0到蓝色 = max)表示 节点中介性node betweenness 。
Betweenness is a centrality measure of a vertex within a graph (there is also edge betweenness, which is not discussed here). Betweenness centrality quantifies the number of times a node acts as a bridge along the shortest path between two other nodes. It was introduced as a measure for quantifying the control of a human on the communication between other humans in a social network by Linton Freeman[30] In his conception, vertices that have a high probability to occur on a randomly chosen shortest path between two randomly chosen vertices have a high betweenness.
Betweenness is a centrality measure of a vertex within a graph (there is also edge betweenness, which is not discussed here). Betweenness centrality quantifies the number of times a node acts as a bridge along the shortest path between two other nodes. It was introduced as a measure for quantifying the control of a human on the communication between other humans in a social network by Linton Freeman In his conception, vertices that have a high probability to occur on a randomly chosen shortest path between two randomly chosen vertices have a high betweenness.
中介性是图中顶点的中心性度量(也有边中介性,这里没有讨论)。中介中心性量化了一个节点沿着其他两个节点之间的最短路径充当桥梁的次数。在林顿 · 弗里曼 Linton Freeman[30]的概念中,它是作为一种量化一个人对社交网络中其他人之间交流控制的度量被引入的,在两个随机选择的顶点之间随机选择的最短路径上出现概率高的顶点具有很高的中介性。
The betweenness of a vertex [math]\displaystyle{ v }[/math] in a graph [math]\displaystyle{ G:=(V,E) }[/math] with [math]\displaystyle{ V }[/math] vertices is computed as follows:
The betweenness of a vertex [math]\displaystyle{ v }[/math] in a graph [math]\displaystyle{ G:=(V,E) }[/math] with [math]\displaystyle{ V }[/math] vertices is computed as follows:
在一个图 < math > g: = (v,e) </math > 与 < math > v </math > 的顶点中介性计算如下:
- For each pair of vertices (s,t), compute the shortest paths between them.
For each pair of vertices (s,t), compute the shortest paths between them.
对于每一对顶点(s,t) ,计算它们之间的最短路径。
- For each pair of vertices (s,t), determine the fraction of shortest paths that pass through the vertex in question (here, vertex v).
For each pair of vertices (s,t), determine the fraction of shortest paths that pass through the vertex in question (here, vertex v).
对于每对顶点(s,t) ,确定通过该顶点(这里是顶点 v)的最短路径的分数。
- Sum this fraction over all pairs of vertices (s,t).
Sum this fraction over all pairs of vertices (s,t).
对所有顶点对(s,t)求这个分数的和。
More compactly the betweenness can be represented as:[31]
More compactly the betweenness can be represented as:
更确切地说,中介性可以表示为:
- [math]\displaystyle{ C_B(v)= \sum_{s \neq v \neq t \in V}\frac{\sigma_{st}(v)}{\sigma_{st}} }[/math]
[math]\displaystyle{ C_B(v)= \sum_{s \neq v \neq t \in V}\frac{\sigma_{st}(v)}{\sigma_{st}} }[/math]
{ math > c _ b (v) = sum _ { s neq v neq t in v } frac { sigma _ st }(v)}{ sigma _ st } </math >
where [math]\displaystyle{ \sigma_{st} }[/math] is total number of shortest paths from node [math]\displaystyle{ s }[/math] to node [math]\displaystyle{ t }[/math] and [math]\displaystyle{ \sigma_{st}(v) }[/math] is the number of those paths that pass through [math]\displaystyle{ v }[/math]. The betweenness may be normalised by dividing through the number of pairs of vertices not including v, which for directed graphs is [math]\displaystyle{ (n-1)(n-2) }[/math] and for undirected graphs is [math]\displaystyle{ (n-1)(n-2)/2 }[/math]. For example, in an undirected star graph, the center vertex (which is contained in every possible shortest path) would have a betweenness of [math]\displaystyle{ (n-1)(n-2)/2 }[/math] (1, if normalised) while the leaves (which are contained in no shortest paths) would have a betweenness of 0.
where [math]\displaystyle{ \sigma_{st} }[/math] is total number of shortest paths from node [math]\displaystyle{ s }[/math] to node [math]\displaystyle{ t }[/math] and [math]\displaystyle{ \sigma_{st}(v) }[/math] is the number of those paths that pass through [math]\displaystyle{ v }[/math]. The betweenness may be normalised by dividing through the number of pairs of vertices not including v, which for directed graphs is [math]\displaystyle{ (n-1)(n-2) }[/math] and for undirected graphs is [math]\displaystyle{ (n-1)(n-2)/2 }[/math]. For example, in an undirected star graph, the center vertex (which is contained in every possible shortest path) would have a betweenness of [math]\displaystyle{ (n-1)(n-2)/2 }[/math] (1, if normalised) while the leaves (which are contained in no shortest paths) would have a betweenness of 0.
其中 < math > sigma { st } </math > 是从节点 < math > s </math > 到节点 < math > t </math > 的最短路径总数,< math > sigma { st }(v) </math > 是通过 < math > v </math > 的路径数。中介性也许可以通过除以不包括V的顶点对的数目被规范化,对于有向图是 < math > (n-1)(n-2) </math > ,对于无向图是 < math > (n-1)(n-2)/2 </math > 。例如,在一个无向星图中,中心顶点(包含在每个可能的最短路径中)的中介性为 < math > (n-1)(n-2)/2 </math > (1,如果标准化) ,而叶节点(包含在没有最短路径中)的中介性为0。
From a calculation aspect, both betweenness and closeness centralities of all vertices in a graph involve calculating the shortest paths between all pairs of vertices on a graph, which requires [math]\displaystyle{ O(V^3) }[/math] time with the Floyd–Warshall algorithm. However, on sparse graphs, Johnson's algorithm may be more efficient, taking [math]\displaystyle{ O(V^2 \log V + V E) }[/math] time. In the case of unweighted graphs the calculations can be done with Brandes' algorithm[31] which takes [math]\displaystyle{ O(V E) }[/math] time. Normally, these algorithms assume that graphs are undirected and connected with the allowance of loops and multiple edges. When specifically dealing with network graphs, often graphs are without loops or multiple edges to maintain simple relationships (where edges represent connections between two people or vertices). In this case, using Brandes' algorithm will divide final centrality scores by 2 to account for each shortest path being counted twice.[31]
From a calculation aspect, both betweenness and closeness centralities of all vertices in a graph involve calculating the shortest paths between all pairs of vertices on a graph, which requires [math]\displaystyle{ O(V^3) }[/math] time with the Floyd–Warshall algorithm. However, on sparse graphs, Johnson's algorithm may be more efficient, taking [math]\displaystyle{ O(V^2 \log V + V E) }[/math] time. In the case of unweighted graphs the calculations can be done with Brandes' algorithm which takes [math]\displaystyle{ O(V E) }[/math] time. Normally, these algorithms assume that graphs are undirected and connected with the allowance of loops and multiple edges. When specifically dealing with network graphs, often graphs are without loops or multiple edges to maintain simple relationships (where edges represent connections between two people or vertices). In this case, using Brandes' algorithm will divide final centrality scores by 2 to account for each shortest path being counted twice.
从计算的角度来看,图中所有顶点的中介中心性和紧密中心性都涉及到计算图中所有顶点对之间的最短路径,采用[math]\displaystyle{ O(V^3) }[/math]时间和 弗洛伊德-沃肖尔 Floyd-Warshall算法。然而,对于稀疏图,约翰逊 Johnson算法的效率可能更高,采用 < math > o (v ^ 2 log v + v e) </math > 时间。在不加权图的情况下,可以用布兰德斯 Brandes 的算法进行计算[31],该算法需要 < math > o (v e) </math > 时间。一般情况下,这些算法假定图是无向的,并且连通图中允许有圈和多条边。当专门处理网络图时,图通常没有环或多条边来维持简单的关系(其中的边表示两个人或顶点之间的联系)。在这种情况下,使用 Brandes 的算法将最终的中心性分数除以2来计算每条被重复计算的最短路径。[31]
Eigenvector centrality
特征向量中心性 Eigenvector centrality
Eigenvector centrality (also called eigencentrality) is a measure of the influence of a node in a network. It assigns relative scores to all nodes in the network based on the concept that connections to high-scoring nodes contribute more to the score of the node in question than equal connections to low-scoring nodes.[32][4] Google's PageRank and the Katz centrality are variants of the eigenvector centrality.[33]
Eigenvector centrality (also called eigencentrality) is a measure of the influence of a node in a network. It assigns relative scores to all nodes in the network based on the concept that connections to high-scoring nodes contribute more to the score of the node in question than equal connections to low-scoring nodes.
特征向量中心性 (也称为特征中心性)是对网络中节点影响的一种度量。它将相对得分分配给网络中的所有节点,这是基于这样一个概念: 连接得分高的节点比连接得分低的节点对得分贡献更大。[34][4]谷歌的网页排名和卡兹中心性是特征向量中心性的变体。[33]
= Using the adjacency matrix to find eigenvector centrality
使用 邻接矩阵The adjacency matrix发现特征向量中心性 Eigenvector centrality
For a given graph [math]\displaystyle{ G:=(V,E) }[/math] with [math]\displaystyle{ |V| }[/math] number of vertices let [math]\displaystyle{ A = (a_{v,t}) }[/math] be the adjacency matrix, i.e. [math]\displaystyle{ a_{v,t} = 1 }[/math] if vertex [math]\displaystyle{ v }[/math] is linked to vertex [math]\displaystyle{ t }[/math], and [math]\displaystyle{ a_{v,t} = 0 }[/math] otherwise. The relative centrality score of vertex [math]\displaystyle{ v }[/math] can be defined as:
For a given graph [math]\displaystyle{ G:=(V,E) }[/math] with [math]\displaystyle{ |V| }[/math] number of vertices let [math]\displaystyle{ A = (a_{v,t}) }[/math] be the adjacency matrix, i.e. [math]\displaystyle{ a_{v,t} = 1 }[/math] if vertex [math]\displaystyle{ v }[/math] is linked to vertex [math]\displaystyle{ t }[/math], and [math]\displaystyle{ a_{v,t} = 0 }[/math] otherwise. The relative centrality score of vertex [math]\displaystyle{ v }[/math] can be defined as:
对于一个给定的图 g: = (v,e) </math > 与 < math > | v | </math >的顶点数 让 < math > a = (a { v,t }) </math > 成为邻接矩阵。即,如果顶点 < math > > v </math > 与 math > t </math > 相连,而 < math > a { v,t } = 0 </math > 不然。顶点 < math > v </math > 的相对中心性评分可以定义为:
- [math]\displaystyle{ x_v = \frac{1}{\lambda} \sum_{t \in M(v)}x_t = \frac{1}{\lambda} \sum_{t \in G} a_{v,t}x_t }[/math]
[math]\displaystyle{ x_v = \frac{1}{\lambda} \sum_{t \in M(v)}x_t = \frac{1}{\lambda} \sum_{t \in G} a_{v,t}x_t }[/math]
在 m (v)} x _ t = frac {1}{ lambda } sum { t in g } a { v,t } x _ t </math >
where [math]\displaystyle{ M(v) }[/math] is a set of the neighbors of [math]\displaystyle{ v }[/math] and [math]\displaystyle{ \lambda }[/math] is a constant. With a small rearrangement this can be rewritten in vector notation as the eigenvector equation
where [math]\displaystyle{ M(v) }[/math] is a set of the neighbors of [math]\displaystyle{ v }[/math] and [math]\displaystyle{ \lambda }[/math] is a constant. With a small rearrangement this can be rewritten in vector notation as the eigenvector equation
其中 < math > m (v) </math > 是 < math >的相邻集合,而< math > > lambda </math >是一个常量。通过一个小的重新排列,这可以用向量符号重写为特征向量方程。
- [math]\displaystyle{ \mathbf{Ax} = {\lambda}\mathbf{x} }[/math]
[math]\displaystyle{ \mathbf{Ax} = {\lambda}\mathbf{x} }[/math]
[ math > mathbf { Ax } = { lambda } mathbf { x } </math >
In general, there will be many different eigenvalues [math]\displaystyle{ \lambda }[/math] for which a non-zero eigenvector solution exists. Since the entries in the adjacency matrix are non-negative, there is a unique largest eigenvalue, which is real and positive, by the Perron–Frobenius theorem. This greatest eigenvalue results in the desired centrality measure.[35] The [math]\displaystyle{ v^{th} }[/math] component of the related eigenvector then gives the relative centrality score of the vertex [math]\displaystyle{ v }[/math] in the network. The eigenvector is only defined up to a common factor, so only the ratios of the centralities of the vertices are well defined. To define an absolute score one must normalise the eigenvector, e.g., such that the sum over all vertices is 1 or the total number of vertices n. Power iteration is one of many eigenvalue algorithms that may be used to find this dominant eigenvector.[33] Furthermore, this can be generalized so that the entries in A can be real numbers representing connection strengths, as in a stochastic matrix.
In general, there will be many different eigenvalues [math]\displaystyle{ \lambda }[/math] for which a non-zero eigenvector solution exists. Since the entries in the adjacency matrix are non-negative, there is a unique largest eigenvalue, which is real and positive, by the Perron–Frobenius theorem. This greatest eigenvalue results in the desired centrality measure. The [math]\displaystyle{ v^{th} }[/math] component of the related eigenvector then gives the relative centrality score of the vertex [math]\displaystyle{ v }[/math] in the network. The eigenvector is only defined up to a common factor, so only the ratios of the centralities of the vertices are well defined. To define an absolute score one must normalise the eigenvector, e.g., such that the sum over all vertices is 1 or the total number of vertices n. Power iteration is one of many eigenvalue algorithms that may be used to find this dominant eigenvector. Furthermore, this can be generalized so that the entries in A can be real numbers representing connection strengths, as in a stochastic matrix.
一般情况下,存在许多不同的特征值< math > > lambda </math >,对于这些特征值存在一个非零特征向量解。由于邻接矩阵中的项是非负的,所以由 佩龙-弗罗贝尼乌斯 Perron- Frobenius定理得出,它有一个唯一的正实数最大特征值。由这个最大的特征值得出期望的中心性度量。[36]相关特征向量的 < math > v ^ { th } </math > 分量给出了网络中顶点 < math > v </math > 的相对中心性评分。特征向量只定义了一个公共因子,所以只有顶点中心性的比例是明确定义的。要定义一个绝对分数,必须对特征向量进行标准化,例如,使所有顶点的和为1或顶点的总数n。幂迭代是许多特征值算法之一,可以用来找到这个主要特征向量。[33]此外,这推广,使得 A中的项可以是表示连接强度的实数,就像在 随机矩阵 Stochastic matrix中一样。
Katz centrality
卡兹中心性 Katz centrality
Katz centrality[37] is a generalization of degree centrality. Degree centrality measures the number of direct neighbors, and Katz centrality measures the number of all nodes that can be connected through a path, while the contributions of distant nodes are penalized. Mathematically, it is defined as
Katz centrality is a generalization of degree centrality. Degree centrality measures the number of direct neighbors, and Katz centrality measures the number of all nodes that can be connected through a path, while the contributions of distant nodes are penalized. Mathematically, it is defined as
卡兹中心性[38]是度中心性的推广。度中心性度量的是直接相邻节点的数量,卡兹中心性度量的是通过一条路径可以连接的所有节点的数量,而远处节点的贡献会受到削减。在数学上,它被定义为
- [math]\displaystyle{ x_i = \sum_{k=1}^{\infin}\sum_{j=1}^N \alpha^k (A^k)_{ji} }[/math]
[math]\displaystyle{ x_i = \sum_{k=1}^{\infin}\sum_{j=1}^N \alpha^k (A^k)_{ji} }[/math]
[数学][数学]
where [math]\displaystyle{ \alpha }[/math] is an attenuation factor in [math]\displaystyle{ (0,1) }[/math].
where [math]\displaystyle{ \alpha }[/math] is an attenuation factor in [math]\displaystyle{ (0,1) }[/math].
其中 < math > alpha </math > 是 < math > (0,1) </math > 中的衰减因子。
Katz centrality can be viewed as a variant of eigenvector centrality. Another form of Katz centrality is
Katz centrality can be viewed as a variant of eigenvector centrality. Another form of Katz centrality is
卡兹中心性可以看作是特征向量中心性的一种变体。卡兹中心性的另一种形式是
- [math]\displaystyle{ x_i = \alpha \sum_{j =1}^N a_{ij}(x_j+1). }[/math]
[math]\displaystyle{ x_i = \alpha \sum_{j =1}^N a_{ij}(x_j+1). }[/math]
(x _ j + 1)
Compared to the expression of eigenvector centrality, [math]\displaystyle{ x_j }[/math] is replaced by [math]\displaystyle{ x_j+1. }[/math]
Compared to the expression of eigenvector centrality, [math]\displaystyle{ x_j }[/math] is replaced by [math]\displaystyle{ x_j+1. }[/math]
与特征向量中心性的表达式相比,< math > x _ j </math > 被 < math > x _ j + 1所代替
It is shown that[39] the principal eigenvector (associated with the largest eigenvalue of [math]\displaystyle{ A }[/math], the adjacency matrix) is the limit of Katz centrality as [math]\displaystyle{ \alpha }[/math] approaches [math]\displaystyle{ \tfrac{1}{\lambda} }[/math] from below.
It is shown that the principal eigenvector (associated with the largest eigenvalue of [math]\displaystyle{ A }[/math], the adjacency matrix) is the limit of Katz centrality as [math]\displaystyle{ \alpha }[/math] approaches [math]\displaystyle{ \tfrac{1}{\lambda} }[/math] from below.
结果表明,[40]主特征向量(与 < math > a </math > ,邻接矩阵的最大特征值相关)是卡兹中心性的极限,当 < math > alpha </math > 从下接近 < math > tfrac {1}{ lambda } </math >时 。
PageRank centrality
网页排名中心性 PageRank centrality
PageRank satisfies the following equation
PageRank satisfies the following equation
网页排名满足下面的等式
- [math]\displaystyle{ x_i = \alpha \sum_{j } a_{ji}\frac{x_j}{L(j)} + \frac{1-\alpha}{N}, }[/math]
[math]\displaystyle{ x_i = \alpha \sum_{j } a_{ji}\frac{x_j}{L(j)} + \frac{1-\alpha}{N}, }[/math]
1-alpha { n } ,</math >
where
where
其中
- [math]\displaystyle{ L(j) = \sum_{i} a_{ji} }[/math]
[math]\displaystyle{ L(j) = \sum_{i} a_{ji} }[/math]
[ math > l (j) = sum { i } a { ji } </math >
is the number of neighbors of node [math]\displaystyle{ j }[/math] (or number of outbound links in a directed graph). Compared to eigenvector centrality and Katz centrality, one major difference is the scaling factor [math]\displaystyle{ L(j) }[/math]. Another difference between PageRank and eigenvector centrality is that the PageRank vector is a left hand eigenvector (note the factor [math]\displaystyle{ a_{ji} }[/math] has indices reversed).[41]
is the number of neighbors of node [math]\displaystyle{ j }[/math] (or number of outbound links in a directed graph). Compared to eigenvector centrality and Katz centrality, one major difference is the scaling factor [math]\displaystyle{ L(j) }[/math]. Another difference between PageRank and eigenvector centrality is that the PageRank vector is a left hand eigenvector (note the factor [math]\displaystyle{ a_{ji} }[/math] has indices reversed).
是节点 < math > j </math > (或有向图中出站链接的数量)的相邻节点数量。与特征向量中心性和卡兹中心性相比,尺度因子 < math > l (j) </math > 是一个主要的区别。网页排名中心性和特征向量中心性的另一个区别是网页排名中心性向量是一个左手特征向量(注意因子 < math > a _ { ji } </math >具有相反的索引)。[42]
Percolation centrality
渗滤中心性 Percolation centrality
A slew of centrality measures exist to determine the ‘importance’ of a single node in a complex network. However, these measures quantify the importance of a node in purely topological terms, and the value of the node does not depend on the ‘state’ of the node in any way. It remains constant regardless of network dynamics. This is true even for the weighted betweenness measures. However, a node may very well be centrally located in terms of betweenness centrality or another centrality measure, but may not be ‘centrally’ located in the context of a network in which there is percolation. Percolation of a ‘contagion’ occurs in complex networks in a number of scenarios. For example, viral or bacterial infection can spread over social networks of people, known as contact networks. The spread of disease can also be considered at a higher level of abstraction, by contemplating a network of towns or population centres, connected by road, rail or air links. Computer viruses can spread over computer networks. Rumours or news about business offers and deals can also spread via social networks of people. In all of these scenarios, a ‘contagion’ spreads over the links of a complex network, altering the ‘states’ of the nodes as it spreads, either recoverably or otherwise. For example, in an epidemiological scenario, individuals go from ‘susceptible’ to ‘infected’ state as the infection spreads. The states the individual nodes can take in the above examples could be binary (such as received/not received a piece of news), discrete (susceptible/infected/recovered), or even continuous (such as the proportion of infected people in a town), as the contagion spreads. The common feature in all these scenarios is that the spread of contagion results in the change of node states in networks. Percolation centrality (PC) was proposed with this in mind, which specifically measures the importance of nodes in terms of aiding the percolation through the network. This measure was proposed by Piraveenan et al.[43]
A slew of centrality measures exist to determine the ‘importance’ of a single node in a complex network. However, these measures quantify the importance of a node in purely topological terms, and the value of the node does not depend on the ‘state’ of the node in any way. It remains constant regardless of network dynamics. This is true even for the weighted betweenness measures. However, a node may very well be centrally located in terms of betweenness centrality or another centrality measure, but may not be ‘centrally’ located in the context of a network in which there is percolation. Percolation of a ‘contagion’ occurs in complex networks in a number of scenarios. For example, viral or bacterial infection can spread over social networks of people, known as contact networks. The spread of disease can also be considered at a higher level of abstraction, by contemplating a network of towns or population centres, connected by road, rail or air links. Computer viruses can spread over computer networks. Rumours or news about business offers and deals can also spread via social networks of people. In all of these scenarios, a ‘contagion’ spreads over the links of a complex network, altering the ‘states’ of the nodes as it spreads, either recoverably or otherwise. For example, in an epidemiological scenario, individuals go from ‘susceptible’ to ‘infected’ state as the infection spreads. The states the individual nodes can take in the above examples could be binary (such as received/not received a piece of news), discrete (susceptible/infected/recovered), or even continuous (such as the proportion of infected people in a town), as the contagion spreads. The common feature in all these scenarios is that the spread of contagion results in the change of node states in networks. Percolation centrality (PC) was proposed with this in mind, which specifically measures the importance of nodes in terms of aiding the percolation through the network. This measure was proposed by Piraveenan et al.
在复杂网络中,存在大量的中心性度量来确定单个节点的“重要性”。然而,这些度量单纯从拓扑学的角度来量化节点的重要性,节点的值并不以任何方式依赖于节点的状态。不管网络动态如何,它都保持不变。即使对于加权的两者之间的度量也是如此。然而,一个节点可能很好地位于中介中心性或其他中心性度量的中心位置,但可能不是位于有渗滤的网络的上下文中的中心位置。在许多情况下,复杂网络中都会出现“传染”的渗滤现象。例如,病毒或细菌感染可以通过人们的社交网络传播,也就是所谓的接触网络。还可以在更高的抽象层次上考虑疾病的传播问题,设想通过公路、铁路或空中连接起来的城镇或人口中心网络。计算机病毒可以通过计算机网络传播。关于商业活动和交易的谣言或新闻也可以通过人们的社交网络传播。在所有这些情况下,一种“传染病”在一个复杂网络的链接上传播,随着它的传播,无论是可恢复的还是不可恢复的,都会改变节点的“状态”。例如,在流行病学方案中,随着感染扩散,个人从”易感”状态转变为”受感染”状态。在上面的例子中,随着传染的扩散,每个节点可以采取的状态可以是二进制的(例如接收/没有接收到一条新闻)、离散的(易感/受感染/康复) ,甚至是连续的(例如一个城镇中受感染的人的比例) 。这些情景的共同特点是,传染的扩散导致网络中节点状态的改变。 渗滤中心性 Percolation centrality(PC)就是基于这个思想而提出的,它特别地度量了节点在协助网络渗滤方面的重要性。这种度量是由皮拉维南 piraveanan等人提出的。[43]
Percolation centrality is defined for a given node, at a given time, as the proportion of ‘percolated paths’ that go through that node. A ‘percolated path’ is a shortest path between a pair of nodes, where the source node is percolated (e.g., infected). The target node can be percolated or non-percolated, or in a partially percolated state.
Percolation centrality is defined for a given node, at a given time, as the proportion of ‘percolated paths’ that go through that node. A ‘percolated path’ is a shortest path between a pair of nodes, where the source node is percolated (e.g., infected). The target node can be percolated or non-percolated, or in a partially percolated state.
渗滤中心性定义为在给定时间内一个给定节点的渗滤路径的比例。“渗滤路径”是一对节点之间的最短路径,其中源节点被渗滤(例如,被感染)。目标节点可以是渗滤的或非渗滤的,或处于部分渗滤状态。
- [math]\displaystyle{ PC^t(v)= \frac{1}{N-2}\sum_{s \neq v \neq r}\frac{\sigma_{sr}(v)}{\sigma_{sr}}\frac{{x^t}_s}{{\sum {[{x^t}_i}]}-{x^t}_v} }[/math]
[math]\displaystyle{ PC^t(v)= \frac{1}{N-2}\sum_{s \neq v \neq r}\frac{\sigma_{sr}(v)}{\sigma_{sr}}\frac{{x^t}_s}{{\sum {[{x^t}_i}]}-{x^t}_v} }[/math]
< math > PC ^ t (v) = frac {1}{ N-2} sum { s neq v neq r } frac { sigma { sr }(v)}{ sigma { sr }} frac { x ^ t }{ sum {[{ x ^ t } i }}}]}}-{ x ^ t }{ v } </math >
where [math]\displaystyle{ \sigma_{sr} }[/math] is total number of shortest paths from node [math]\displaystyle{ s }[/math] to node [math]\displaystyle{ r }[/math] and [math]\displaystyle{ \sigma_{sr}(v) }[/math] is the number of those paths that pass through [math]\displaystyle{ v }[/math]. The percolation state of the node [math]\displaystyle{ i }[/math] at time [math]\displaystyle{ t }[/math] is denoted by [math]\displaystyle{ {x^t}_i }[/math] and two special cases are when [math]\displaystyle{ {x^t}_i=0 }[/math] which indicates a non-percolated state at time [math]\displaystyle{ t }[/math] whereas when [math]\displaystyle{ {x^t}_i=1 }[/math] which indicates a fully percolated state at time [math]\displaystyle{ t }[/math]. The values in between indicate partially percolated states ( e.g., in a network of townships, this would be the percentage of people infected in that town).
where [math]\displaystyle{ \sigma_{sr} }[/math] is total number of shortest paths from node [math]\displaystyle{ s }[/math] to node [math]\displaystyle{ r }[/math] and [math]\displaystyle{ \sigma_{sr}(v) }[/math] is the number of those paths that pass through [math]\displaystyle{ v }[/math]. The percolation state of the node [math]\displaystyle{ i }[/math] at time [math]\displaystyle{ t }[/math] is denoted by [math]\displaystyle{ {x^t}_i }[/math] and two special cases are when [math]\displaystyle{ {x^t}_i=0 }[/math] which indicates a non-percolated state at time [math]\displaystyle{ t }[/math] whereas when [math]\displaystyle{ {x^t}_i=1 }[/math] which indicates a fully percolated state at time [math]\displaystyle{ t }[/math]. The values in between indicate partially percolated states ( e.g., in a network of townships, this would be the percentage of people infected in that town).
其中 < math > σ { sr } </math > 是从节点 < math > s </math > 到节点 < math > r </math >的最短路径的总数, < math > sigma { sr }(v) </math > 是通过 < math > v </math > 的路径的总数。在时间 < math > t </math > 时,节点< math > i</math >的渗滤状态用 < math > { x ^ t } _ i </math > 表示,两个特殊情况是当 < math > { x ^ t } _ i = 0 </math > 表示在时间上是非渗滤状态,而当 < math > < x ^ t </math > i = 1 </math > 表示在时间上是完全渗滤状态。两者之间的值表示部分渗滤状态(例如,在一个城镇网络中,这是该城镇感染者的百分比)。
The attached weights to the percolation paths depend on the percolation levels assigned to the source nodes, based on the premise that the higher the percolation level of a source node is, the more important are the paths that originate from that node. Nodes which lie on shortest paths originating from highly percolated nodes are therefore potentially more important to the percolation. The definition of PC may also be extended to include target node weights as well. Percolation centrality calculations run in [math]\displaystyle{ O(NM) }[/math] time with an efficient implementation adopted from Brandes' fast algorithm and if the calculation needs to consider target nodes weights, the worst case time is [math]\displaystyle{ O(N^3) }[/math].
The attached weights to the percolation paths depend on the percolation levels assigned to the source nodes, based on the premise that the higher the percolation level of a source node is, the more important are the paths that originate from that node. Nodes which lie on shortest paths originating from highly percolated nodes are therefore potentially more important to the percolation. The definition of PC may also be extended to include target node weights as well. Percolation centrality calculations run in [math]\displaystyle{ O(NM) }[/math] time with an efficient implementation adopted from Brandes' fast algorithm and if the calculation needs to consider target nodes weights, the worst case time is [math]\displaystyle{ O(N^3) }[/math].
渗流路径的权重取决于分配给源节点的渗滤水平,前提是源节点的渗滤水平越高,源节点的路径就越重要。因此,位于源自高渗滤节点的最短路径上的节点可能对渗滤更为重要。PC 的定义也可以扩展到包括目标节点的权重。渗滤中心性计算运行在 < math > o (NM) </math > 时间,高效的实现采用了布兰德斯快速算法,如果计算需要考虑目标节点的权重,最坏情况下时间为 < math > o (n ^ 3) </math > 。
Cross-clique centrality
跨团中心性 Cross-clique centrality
Cross-clique centrality of a single node in a complex graph determines the connectivity of a node to different cliques. A node with high cross-clique connectivity facilitates the propagation of information or disease in a graph. Cliques are subgraphs in which every node is connected to every other node in the clique. The cross-clique connectivity of a node [math]\displaystyle{ v }[/math] for a given graph [math]\displaystyle{ G:=(V,E) }[/math] with [math]\displaystyle{ |V| }[/math] vertices and [math]\displaystyle{ |E| }[/math] edges, is defined as [math]\displaystyle{ X(v) }[/math] where [math]\displaystyle{ X(v) }[/math] is the number of cliques to which vertex [math]\displaystyle{ v }[/math] belongs. This measure was used in [44] but was first proposed by Everett and Borgatti in 1998 where they called it clique-overlap centrality.
Cross-clique centrality of a single node in a complex graph determines the connectivity of a node to different cliques. A node with high cross-clique connectivity facilitates the propagation of information or disease in a graph. Cliques are subgraphs in which every node is connected to every other node in the clique. The cross-clique connectivity of a node [math]\displaystyle{ v }[/math] for a given graph [math]\displaystyle{ G:=(V,E) }[/math] with [math]\displaystyle{ |V| }[/math] vertices and [math]\displaystyle{ |E| }[/math] edges, is defined as [math]\displaystyle{ X(v) }[/math] where [math]\displaystyle{ X(v) }[/math] is the number of cliques to which vertex [math]\displaystyle{ v }[/math] belongs. This measure was used in but was first proposed by Everett and Borgatti in 1998 where they called it clique-overlap centrality.
复杂图中单个节点的跨团中心性决定了一个节点与不同团的连通性。具有高度跨团连通性的节点有利于信息或疾病在图中的传播。团是一种 子图 Subgraphs,团中的每个节点都与团中的其他节点相连。对于一个给定的图 g: = (v,e) </math > 与 < math > | v | </math > 顶点和 < math > | e | </math > 边的跨团连通性,定义为 < math > x (v) </math > x (v) </math > 其中 < math > x (v) </math > 是 < math > v </math > 所属的顶点团数。这个度量应用日久,[44]但是在1998年由埃弗莱特 Everett 和博加提 Borgatti 首次提出,他们称之为 派系重叠中心性 Clique-overlap centrality。
Freeman centralization
弗里曼中心度Freeman centralization
The centralization of any network is a measure of how central its most central node is in relation to how central all the other nodes are.[15] Centralization measures then (a) calculate the sum in differences in centrality between the most central node in a network and all other nodes; and (b) divide this quantity by the theoretically largest such sum of differences in any network of the same size.[15] Thus, every centrality measure can have its own centralization measure. Defined formally, if [math]\displaystyle{ C_x(p_i) }[/math] is any centrality measure of point [math]\displaystyle{ i }[/math], if [math]\displaystyle{ C_x(p_*) }[/math] is the largest such measure in the network, and if:
The centralization of any network is a measure of how central its most central node is in relation to how central all the other nodes are. Centralization measures then (a) calculate the sum in differences in centrality between the most central node in a network and all other nodes; and (b) divide this quantity by the theoretically largest such sum of differences in any network of the same size. Thus, every centrality measure can have its own centralization measure. Defined formally, if [math]\displaystyle{ C_x(p_i) }[/math] is any centrality measure of point [math]\displaystyle{ i }[/math], if [math]\displaystyle{ C_x(p_*) }[/math] is the largest such measure in the network, and if:
任何网络的中心度都是衡量其最核心的节点相对于其他所有节点的集聚程度的标准。[15]中心度的度量方法是: (a)计算网络中最中心的节点与所有其他节点之间的中心性差异之和; (b)将这个数量除以理论上相同规模的任何网络中这种差异之和的最大值。[15]因此,每个中心性度量都可以有自己的中心度度量。正式定义,如果 < math > c _ x (p _ i) </math > 是点 < math > i </math > 的中心性度量,如果 < math > c _ x (p _ *) </math > 是网络中最大的中心性度量,如果:
- [math]\displaystyle{ \max \sum_{i=1}^{N} C_x(p_*)-C_x(p_i) }[/math]
[math]\displaystyle{ \max \sum_{i=1}^{N} C_x(p_*)-C_x(p_i) }[/math]
< math > max sum { i = 1} ^ { n } c _ x (p _ *)-c _ x (p _ i) </math >
is the largest sum of differences in point centrality [math]\displaystyle{ C_x }[/math] for any graph with the same number of nodes, then the centralization of the network is:[15]
is the largest sum of differences in point centrality [math]\displaystyle{ C_x }[/math] for any graph with the same number of nodes, then the centralization of the network is:
是具有相同节点数的任何图的点中心性的最大差值之和,然后网络中心度是:
- [math]\displaystyle{ C_x=\frac{\sum_{i=1}^{N} C_x(p_*)-C_x(p_i)}{\max \sum_{i=1}^{N} C_x(p_*)-C_x(p_i)}. }[/math]
[math]\displaystyle{ C_x=\frac{\sum_{i=1}^{N} C_x(p_*)-C_x(p_i)}{\max \sum_{i=1}^{N} C_x(p_*)-C_x(p_i)}. }[/math]
< math > c _ x = frac { sum _ { i = 1} ^ { n } c _ x (p _ *)-c _ x (p _ i)}{ max sum _ { i = 1 ^ { n } c _ x (p _ *)-c _ x (p _ i)} . </math >
Dissimilarity based centrality measures
基于相异性的中心性度量
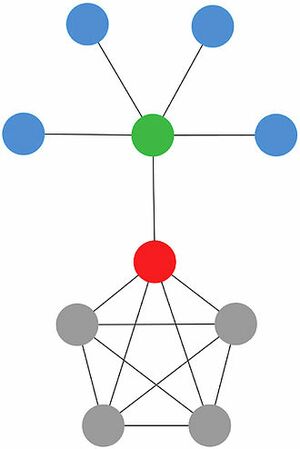
In the illustrated network, green and red nodes are the most dissimilar because they do not share neighbors between them. So, the green one contributes more to the centrality of the red one than the gray ones, because the red one can access to the blue ones only through the green, and the gray nodes are redundant for the red one, because it can access directly to each gray node without any intermediary.
在图示的网络中,绿色节点和红色节点最不相似,因为它们之间不共享相邻节点。因此,绿色的节点比灰色的节点对红色节点的中心性的贡献更大,因为红色的节点只能通过绿色访问蓝色的节点,而灰色的节点对于红色的节点是多余的,因为它可以直接访问每个灰色的节点,而不需要任何中介。
In order to obtain better results in the ranking of the nodes of a given network, in [45] are used dissimilarity measures (specific to the theory of classification and data mining) to enrich the centrality measures in complex networks. This is illustrated with eigenvector centrality, calculating the centrality of each node through the solution of the eigenvalue problem
In order to obtain better results in the ranking of the nodes of a given network, in are used dissimilarity measures (specific to the theory of classification and data mining) to enrich the centrality measures in complex networks. This is illustrated with eigenvector centrality, calculating the centrality of each node through the solution of the eigenvalue problem
为了在给定网络节点的排序中获得更好的结果,[46]在复杂网络中使用了相异性度量(特定于分类和数据挖掘理论)来丰富中心性度量。用特征向量中心性来说明,通过求解特征值问题来计算每个节点的中心性。
- [math]\displaystyle{ W\mathbf{c}=\lambda \mathbf{c} }[/math]
[math]\displaystyle{ W\mathbf{c}=\lambda \mathbf{c} }[/math]
数学,数学
where [math]\displaystyle{ W_{ij}=A_{ij}D_{ij} }[/math] (coordinate-to-coordinate product) and [math]\displaystyle{ D_{ij} }[/math] is an arbitrary dissimilarity matrix, defined through a dissimilitary measure, e.g., Jaccard dissimilarity given by
where [math]\displaystyle{ W_{ij}=A_{ij}D_{ij} }[/math] (coordinate-to-coordinate product) and [math]\displaystyle{ D_{ij} }[/math] is an arbitrary dissimilarity matrix, defined through a dissimilitary measure, e.g., Jaccard dissimilarity given by
这里 < math > w { ij } = a { ij } d { ij } </math > (coordinate-to-coordinate product)和 < math > d { ij } </math > 是一个任意的不相似矩阵,通过一个相异性度量来定义,例如,杰卡德 Jaccard相异性由以下给出。
- [math]\displaystyle{ D_{ij}=1-\dfrac{|V^{+}(i)\cap V^{+}(j)|}{|V^{+}(i)\cup V^{+}(j)|} }[/math]
[math]\displaystyle{ D_{ij}=1-\dfrac{|V^{+}(i)\cap V^{+}(j)|}{|V^{+}(i)\cup V^{+}(j)|} }[/math]
1-dfrac { | v ^ { + }(i) cap v ^ { + }(j) | }{ | v ^ { + }(i) cup v ^ { + }(j) | } </math >
Where this measure permits us to quantify the topological contribution (which is why is called contribution centrality) of each node to the centrality of a given node, having more weight/relevance those nodes with greater dissimilarity, since these allow to the given node access to nodes that which themselves can not access directly.
Where this measure permits us to quantify the topological contribution (which is why is called contribution centrality) of each node to the centrality of a given node, having more weight/relevance those nodes with greater dissimilarity, since these allow to the given node access to nodes that which themselves can not access directly.
这种度量允许我们量化每个节点对给定节点中心性的拓扑贡献(这就是为什么我们称之为贡献中心性) ,对那些相异性较大的节点有更多的权重/相关性,因为这些节点允许给定的节点访问那些它们自己不能直接访问的节点。
Is noteworthy that [math]\displaystyle{ W }[/math] is non-negative because [math]\displaystyle{ A }[/math] and [math]\displaystyle{ D }[/math] are non-negative matrices, so we can use the Perron–Frobenius theorem to ensure that the above problem has a unique solution for λ = λmax with c non-negative, allowing us to infer the centrality of each node in the network. Therefore, the centrality of the i-th node is
Is noteworthy that [math]\displaystyle{ W }[/math] is non-negative because [math]\displaystyle{ A }[/math] and [math]\displaystyle{ D }[/math] are non-negative matrices, so we can use the Perron–Frobenius theorem to ensure that the above problem has a unique solution for λ = λmax with c non-negative, allowing us to infer the centrality of each node in the network. Therefore, the centrality of the i-th node is
值得注意的是,< math > w </math > 是非负的,因为 < math > a </math > 和 < math > d </math > 都是非负矩阵,所以我们可以使用Perron–Frobenius定理来确保上述问题对于 c 非负的 = < sub > max 有唯一的解,这样我们就可以推断出网络中每个节点的中心性。因此,i-th 节点的中心性为
- [math]\displaystyle{ c_i=\dfrac{1}{n}\sum_{j=1}^{n}W_{ij}c_{j}, \,\,\,\,\,\, j=1,\cdots,n }[/math]
[math]\displaystyle{ c_i=\dfrac{1}{n}\sum_{j=1}^{n}W_{ij}c_{j}, \,\,\,\,\,\, j=1,\cdots,n }[/math]
1{ n } sum { j = 1} ^ { n } w { ij } c { j } ,,,,,j = 1,cdots,n </math >
where [math]\displaystyle{ n }[/math] is the number of the nodes in the network. Several dissimilarity measures and networks were tested in [47] obtaining improved results in the studied cases.
where [math]\displaystyle{ n }[/math] is the number of the nodes in the network. Several dissimilarity measures and networks were tested in obtaining improved results in the studied cases.
其中 < math > n </math > 是网络中的节点数。在所研究的案例中,为了获得改进的结果,测试了一些相异性度量和网络被测试。[48]
Extensions
扩展
Empirical and theoretical research have extended the concept of centrality in the context of static networks to dynamic centrality[49] in the context of time-dependent and temporal networks.[50][51][52]
Empirical and theoretical research have extended the concept of centrality in the context of static networks to dynamic centrality in the context of time-dependent and temporal networks.
经验和理论研究已经将静态网络中的中心性概念扩展到时间依赖网络和时间网络中的动态中心性。[53][54][55]
For generalizations to weighted networks, see Opsahl et al. (2010).[56]
For generalizations to weighted networks, see Opsahl et al. (2010).
对加权网络的推广,见 Opsahl 等人。(2010). [57]
The concept of centrality was extended to a group level as well. For example, group betweenness centrality shows the proportion of geodesics connecting pairs of non-group members that pass through the group.[58][59]
The concept of centrality was extended to a group level as well. For example, group betweenness centrality shows the proportion of geodesics connecting pairs of non-group members that pass through the group.
中心性的概念也扩展到了群体层次。例如,组间的中介中心性显示了连接穿过组的成对非组成员的测地线的比例。[58][59]
See also
又及
- 阿尔法中心性
- 核心—外围结构
- 距离(图理论)图中的距离
Notes and references
- ↑ 1.0 1.1 Newman, M.E.J. 2010. Networks: An Introduction. Oxford, UK: Oxford University Press.
- ↑ 2.0 2.1 2.2 2.3 2.4 2.5 2.6 2.7 Bonacich, Phillip (1987). "Power and Centrality: A Family of Measures". American Journal of Sociology. 92 (5): 1170–1182. doi:10.1086/228631.
- ↑ 3.00 3.01 3.02 3.03 3.04 3.05 3.06 3.07 3.08 3.09 3.10 Borgatti, Stephen P. (2005). "Centrality and Network Flow". Social Networks. 27: 55–71. CiteSeerX 10.1.1.387.419. doi:10.1016/j.socnet.2004.11.008.
- ↑ 4.0 4.1 4.2 4.3 Christian F. A. Negre, Uriel N. Morzan, Heidi P. Hendrickson, Rhitankar Pal, George P. Lisi, J. Patrick Loria, Ivan Rivalta, Junming Ho, Victor S. Batista. (2018). "Eigenvector centrality for characterization of protein allosteric pathways". Proceedings of the National Academy of Sciences. 115 (52): E12201–E12208. doi:10.1073/pnas.1810452115. PMC 6310864. PMID 30530700.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ↑ 5.0 5.1 5.2 5.3 5.4 5.5 5.6 5.7 Borgatti, Stephen P.; Everett, Martin G. (2006). "A Graph-Theoretic Perspective on Centrality". Social Networks. 28 (4): 466–484. doi:10.1016/j.socnet.2005.11.005.
- ↑ 6.0 6.1 6.2 6.3 Benzi, Michele; Klymko, Christine (2013). "A matrix analysis of different centrality measures". SIAM Journal on Matrix Analysis and Applications. 36 (2): 686–706. arXiv:1312.6722. doi:10.1137/130950550.
- ↑ Michalak, Aadithya, Szczepański, Ravindran, & Jennings 模板:ArXiv
- ↑ Michalak, Aadithya, Szczepański, Ravindran, & Jennings 模板:ArXiv
- ↑ Hu, Xingwei; Shapley, Lloyd (2003). "On Authority Distributions in Organizations". Games and Economic Behavior. 45: 132–170. doi:10.1016/s0899-8256(03)00130-1.
- ↑ Hu, Xingwei (2020). "Sorting big data by revealed preference with application to college ranking". Journal of Big Data. 7. doi:10.1186/s40537-020-00300-1.
- ↑ Hu, Xingwei; Shapley, Lloyd (2003). "On Authority Distributions in Organizations". Games and Economic Behavior. 45: 132–170. doi:10.1016/s0899-8256(03)00130-1.
- ↑ Hu, Xingwei (2020). "Sorting big data by revealed preference with application to college ranking". Journal of Big Data. 7. doi:10.1186/s40537-020-00300-1.
- ↑ Krackhardt, David (June 1990). "Assessing the Political Landscape: Structure, Cognition, and Power in Organizations". Administrative Science Quarterly. 35 (2): 342–369. doi:10.2307/2393394. JSTOR 2393394.
- ↑ Krackhardt, David (June 1990). "Assessing the Political Landscape: Structure, Cognition, and Power in Organizations". Administrative Science Quarterly. 35 (2): 342–369. doi:10.2307/2393394. JSTOR 2393394.
- ↑ 15.0 15.1 15.2 15.3 15.4 15.5 15.6 Freeman, Linton C. (1979), "centrality in social networks: Conceptual clarification" (PDF), Social Networks, 1 (3): 215–239, CiteSeerX 10.1.1.227.9549, doi:10.1016/0378-8733(78)90021-7, archived from the original (PDF) on 2016-02-22, retrieved 2014-07-31
- ↑ 16.0 16.1 16.2 Lawyer, Glenn (2015). "Understanding the spreading power of all nodes in a network: a continuous-time perspective". Sci Rep. 5: 8665. arXiv:1405.6707. Bibcode:2015NatSR...5E8665L. doi:10.1038/srep08665. PMC 4345333. PMID 25727453.
- ↑ 17.0 17.1 da Silva, Renato; Viana, Matheus; da F. Costa, Luciano (2012). "Predicting epidemic outbreak from individual features of the spreaders". J. Stat. Mech.: Theory Exp. 2012 (7): P07005. arXiv:1202.0024. Bibcode:2012JSMTE..07..005A. doi:10.1088/1742-5468/2012/07/p07005.
- ↑ 18.0 18.1 Bauer, Frank; Lizier, Joseph (2012). "Identifying influential spreaders and efficiently estimating infection numbers in epidemic models: A walk counting approach". Europhys Lett. 99 (6): 68007. arXiv:1203.0502. Bibcode:2012EL.....9968007B. doi:10.1209/0295-5075/99/68007.
- ↑ 19.0 19.1 Sikic, Mile; Lancic, Alen; Antulov-Fantulin, Nino; Stefanic, Hrvoje (2013). "Epidemic centrality -- is there an underestimated epidemic impact of network peripheral nodes?". The European Physical Journal B. 86 (10): 1–13. arXiv:1110.2558. Bibcode:2013EPJB...86..440S. doi:10.1140/epjb/e2013-31025-5.
- ↑ 20.0 20.1 Ghoshal, G.; Barabsi, A L (2011). "Ranking stability and super-stable nodes in complex networks". Nat Commun. 2: 394. Bibcode:2011NatCo...2..394G. doi:10.1038/ncomms1396. PMID 21772265.
- ↑ Freeman, Linton C. "Centrality in social networks conceptual clarification." Social networks 1.3 (1979): 215–239.
- ↑ Freeman, Linton C. "Centrality in social networks conceptual clarification." Social networks 1.3 (1979): 215–239.
- ↑ Alex Bavelas. Communication patterns in task-oriented groups. J. Acoust. Soc. Am, 22(6):725–730, 1950.
- ↑ Sabidussi, G (1966). "The centrality index of a graph". Psychometrika. 31 (4): 581–603. doi:10.1007/bf02289527. hdl:10338.dmlcz/101401. PMID 5232444.
- ↑ 25.0 25.1 Marchiori, Massimo; Latora, Vito (2000), "Harmony in the small-world", Physica A: Statistical Mechanics and Its Applications, 285 (3–4): 539–546, arXiv:cond-mat/0008357, Bibcode:2000PhyA..285..539M, doi:10.1016/s0378-4371(00)00311-3
- ↑ Dekker, Anthony (2005). "Conceptual Distance in Social Network Analysis". Journal of Social Structure. 6 (3).
- ↑ Yannick Rochat. Closeness centrality extended to unconnected graphs: The harmonic centrality index (PDF). Applications of Social Network Analysis, ASNA 2009.
- ↑ Dekker, Anthony (2005). "Conceptual Distance in Social Network Analysis". Journal of Social Structure. 6 (3).
- ↑ Yannick Rochat. Closeness centrality extended to unconnected graphs: The harmonic centrality index (PDF). Applications of Social Network Analysis, ASNA 2009.
- ↑ 30.0 30.1 Freeman, Linton (1977). "A set of measures of centrality based upon betweenness". Sociometry. 40 (1): 35–41. doi:10.2307/3033543. JSTOR 3033543.
- ↑ 31.0 31.1 31.2 31.3 31.4 Brandes, Ulrik (2001). "A faster algorithm for betweenness centrality" (PDF). Journal of Mathematical Sociology. 25 (2): 163–177. CiteSeerX 10.1.1.11.2024. doi:10.1080/0022250x.2001.9990249. Retrieved October 11, 2011.
- ↑ M. E. J. Newman. "The mathematics of networks" (PDF). Retrieved 2006-11-09.
{{cite journal}}: Cite journal requires|journal=(help) - ↑ 33.0 33.1 33.2 33.3 "American Mathematical Society".
- ↑ M. E. J. Newman. "The mathematics of networks" (PDF). Retrieved 2006-11-09.
{{cite journal}}: Cite journal requires|journal=(help) - ↑ M. E. J. Newman. "The mathematics of networks" (PDF). Retrieved 2006-11-09.
{{cite journal}}: Cite journal requires|journal=(help) - ↑ M. E. J. Newman. "The mathematics of networks" (PDF). Retrieved 2006-11-09.
{{cite journal}}: Cite journal requires|journal=(help) - ↑ Katz, L. 1953. A New Status Index Derived from Sociometric Index. Psychometrika, 39–43.
- ↑ Katz, L. 1953. A New Status Index Derived from Sociometric Index. Psychometrika, 39–43.
- ↑ Bonacich, P (1991). "Simultaneous group and individual centralities". Social Networks. 13 (2): 155–168. doi:10.1016/0378-8733(91)90018-o.
- ↑ Bonacich, P (1991). "Simultaneous group and individual centralities". Social Networks. 13 (2): 155–168. doi:10.1016/0378-8733(91)90018-o.
- ↑ How does Google rank webpages? -{zh-cn:互联网档案馆; zh-tw:網際網路檔案館; zh-hk:互聯網檔案館;}-的存檔,存档日期January 31, 2012,. 20Q: About Networked Life
- ↑ How does Google rank webpages? -{zh-cn:互联网档案馆; zh-tw:網際網路檔案館; zh-hk:互聯網檔案館;}-的存檔,存档日期January 31, 2012,. 20Q: About Networked Life
- ↑ 43.0 43.1 Piraveenan, M.; Prokopenko, M.; Hossain, L. (2013). "Percolation Centrality: Quantifying Graph-Theoretic Impact of Nodes during Percolation in Networks". PLOS One. 8 (1): e53095. Bibcode:2013PLoSO...853095P. doi:10.1371/journal.pone.0053095. PMC 3551907. PMID 23349699.
- ↑ 44.0 44.1 Faghani, Mohamamd Reza (2013). "A Study of XSS Worm Propagation and Detection Mechanisms in Online Social Networks". IEEE Transactions on Information Forensics and Security. 8 (11): 1815–1826. doi:10.1109/TIFS.2013.2280884.
- ↑ Alvarez-Socorro, A. J.; Herrera-Almarza, G. C.; González-Díaz, L. A. (2015-11-25). "Eigencentrality based on dissimilarity measures reveals central nodes in complex networks". Scientific Reports. 5: 17095. Bibcode:2015NatSR...517095A. doi:10.1038/srep17095. PMC 4658528. PMID 26603652.
- ↑ Alvarez-Socorro, A. J.; Herrera-Almarza, G. C.; González-Díaz, L. A. (2015-11-25). "Eigencentrality based on dissimilarity measures reveals central nodes in complex networks". Scientific Reports. 5: 17095. Bibcode:2015NatSR...517095A. doi:10.1038/srep17095. PMC 4658528. PMID 26603652.
- ↑ Alvarez-Socorro, A.J.; Herrera-Almarza; González-Díaz, L. A. "Supplementary Information for Eigencentrality based on dissimilarity measures reveals central nodes in complex networks" (PDF). Nature Publishing Group.
- ↑ Alvarez-Socorro, A.J.; Herrera-Almarza; González-Díaz, L. A. "Supplementary Information for Eigencentrality based on dissimilarity measures reveals central nodes in complex networks" (PDF). Nature Publishing Group.
- ↑ Braha, D.; Bar-Yam, Y. (2006). "From Centrality to Temporary Fame: Dynamic Centrality in Complex Networks". Complexity. 12 (2): 59–63. arXiv:physics/0611295. Bibcode:2006Cmplx..12b..59B. doi:10.1002/cplx.20156.
- ↑ Hill, S.A.; Braha, D. (2010). "Dynamic Model of Time-Dependent Complex Networks". Physical Review E. 82 (4): 046105. arXiv:0901.4407. Bibcode:2010PhRvE..82d6105H. doi:10.1103/physreve.82.046105. PMID 21230343.
- ↑ Gross, T. and Sayama, H. (Eds.). 2009. Adaptive Networks: Theory, Models and Applications. Springer.
- ↑ Holme, P. and Saramäki, J. 2013. Temporal Networks. Springer.
- ↑ Hill, S.A.; Braha, D. (2010). "Dynamic Model of Time-Dependent Complex Networks". Physical Review E. 82 (4): 046105. arXiv:0901.4407. Bibcode:2010PhRvE..82d6105H. doi:10.1103/physreve.82.046105. PMID 21230343.
- ↑ Gross, T. and Sayama, H. (Eds.). 2009. Adaptive Networks: Theory, Models and Applications. Springer.
- ↑ Holme, P. and Saramäki, J. 2013. Temporal Networks. Springer.
- ↑ Opsahl, Tore; Agneessens, Filip; Skvoretz, John (2010). "Node centrality in weighted networks: Generalizing degree and shortest paths". Social Networks. 32 (3): 245–251. doi:10.1016/j.socnet.2010.03.006. Archived from the original on 2018-02-26. Retrieved 2010-04-23.
- ↑ Opsahl, Tore; Agneessens, Filip; Skvoretz, John (2010). "Node centrality in weighted networks: Generalizing degree and shortest paths". Social Networks. 32 (3): 245–251. doi:10.1016/j.socnet.2010.03.006. Archived from the original on 2018-02-26. Retrieved 2010-04-23.
- ↑ 58.0 58.1 Everett, M. G. and Borgatti, S. P. (2005). Extending centrality. In P. J. Carrington, J. Scott and S. Wasserman (Eds.), Models and methods in social network analysis (pp. 57–76). New York: Cambridge University Press.
- ↑ 59.0 59.1 Puzis, R., Yagil, D., Elovici, Y., Braha, D. (2009).Collaborative attack on Internet users’ anonymity -{zh-cn:互联网档案馆; zh-tw:網際網路檔案館; zh-hk:互聯網檔案館;}-的存檔,存档日期2013-12-07., Internet Research 19(1)
Further reading
拓展阅读
- Koschützki, D.; Lehmann, K. A.; Peeters, L.; Richter, S.; Tenfelde-Podehl, D. and Zlotowski, O. (2005) Centrality Indices. In Brandes, U. and Erlebach, T. (Eds.) Network Analysis: Methodological Foundations, pp. 16–61, LNCS 3418, Springer-Verlag.
Category:Graph theory
分类: 图论
Category:Graph algorithms
分类: 图形算法
Category:Algebraic graph theory
分类: 代数图论
Category:Networks
分类: 网络
Category:Network analysis
分类: 网络分析
Category:Network theory
分类: 网络理论
This page was moved from wikipedia:en:Centrality. Its edit history can be viewed at 网络中心性/edithistory
- CS1 maint: multiple names: authors list
- CS1 errors: missing periodical
- Webarchive模板wayback链接
- Articles with hatnote templates targeting a nonexistent page
- All articles with unsourced statements
- Articles with unsourced statements from September 2015
- Articles with invalid date parameter in template
- 含有受损文件链接的页面
- Graph theory
- Graph algorithms
- Algebraic graph theory
- Networks
- Network analysis
- Network theory
- 待整理页面