KS检验

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
跳到导航 跳到搜索

此词条由Jie翻译。由Lincent审校。

Kolmogorov–Smirnov统计数据的图示。 红线是累积分布函数，蓝线是经验分布函数，黑色箭头是K–S统计量。

在统计学中， Kolmogorov–Smirnov检验（亦称K-S检验或KS检验）是一种连续（或不连续，请参见第2.2节）的一维概率分布均等性的非参数检验，可用于比较一个样本与一个参考概率分布（单一样本K-S检验），或比较两个样本（两个样本的K-S检验）。它是以安德雷·柯尔莫哥洛夫 Andrey Kolmogorov和尼古莱·斯米尔诺夫 Nikolai Smirnov的名字命名。


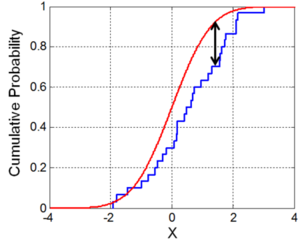
Kolmogorov-Smirnov统计定量描述了一个样本分布的经验分布函数 Empirical distribution function与一个参考分布的累积分布函数 Cumulative distribution function之间的距离，或者是两个样本分布的经验分布函数之间的距离。该统计量的零分布 Null distribution是基于零假设Null hypothesis（或称原始假设）下计算的，可以从参考分布中抽取样本（在单个样本的情况下），或者从相同分布中抽取样本组（在两个样本的情况下）。在单样本情况下，零假设（原假设）考虑的分布可能是连续的（请参阅第2节），纯离散的或混合的（请参阅第2.2节）。然而在考虑两个样本情况下（请参阅第3节），零假设下的分布仅能确定为连续分布，在其他方面并不受限制。


K–S双样本检验是比较两个样本分布最有用，也是最通用的非参数方法之一，因为在对比两个样本时，K-S检验对其经验累积分布函数的位置和形状差异具有一定的敏感性。


Kolmogorov–Smirnov检验经过修改以后可以作为拟合优度检验 goodness of fit test。在测试分布正态性的特殊情况下，将样本先标准化再与标准正态分布进行比较。这相当于将参考分布的均值和方差设置为与样本估计值相等。显然，使用这些值和方差来定义特定参考分布会更改检验统计量的零分布（请参阅使用估算参数进行检验）。各种研究发现，即使采用这种校正形式，该测试也不能像夏皮罗一威尔克 Shapiro-Wilk检验或安德森·达林 Anderson-Darling检验那样有效地检验正态性。当然，这些检验方法也有其自身的缺点。例如，Shapiro–Wilk检验在具有许多相同值的样本中效果并不好。


Kolmogorov-Smirnov统计

n 个独立且同分布（i.i.d.）的有序观测值Xi的经验分布函数Fn定义为：


[math]\displaystyle{ F_n(x)={1 \over n}\sum_{i=1}^n I_{[-\infty,x]}(X_i) }[/math]


其中 [math]\displaystyle{ I_{[-\infty,x]}(X_i) }[/math]是指标函数，如果[math]\displaystyle{ X_i \le x }[/math]等于1，否则等于0。


给定累积分布函数 [math]\displaystyle{ F(x) }[/math]的Kolmogorov–Smirnov统计量为：


[math]\displaystyle{ D_n= \sup_x |F_n(x)-F(x)| }[/math]


其中[math]\displaystyle{ \sup_x }[/math]是距离集的上限值。根据格利文科·坎泰利 Glivenko-Cantelli定理，如果样本来自分布[math]\displaystyle{ F(x) }[/math]，则当n变为无穷大时，[math]\displaystyle{ Dn }[/math]几乎肯定会收敛于0。科尔莫戈罗夫 Kolmogorov通过有效加入收敛速率来增强此结果（请参阅Kolmogorov分布）。另外Donsker定理提供了更有力的结果。


在实践中，该统计需要相对大量的数据点（与其他拟合优度标准相比，例如Anderson-Darling检验统计）才能正确地拒绝零假设。

Kolmogorov distribution Kolmogorov 分布

Kolmogorov分布是随机变量的分布


[math]\displaystyle{ K=\sup_{t\in[0,1]}|B(t)| }[/math]


其中[math]\displaystyle{ B(t) }[/math]是布朗 Brownian桥。K的累积分布函数为


[math]\displaystyle{ \operatorname{Pr}(K\leq x)=1-2\sum_{k=1}^\infty (-1)^{k-1} e^{-2k^2 x^2}=\frac{\sqrt{2\pi}}{x}\sum_{k=1}^\infty e^{-(2k-1)^2\pi^2/(8x^2)} }[/math],


也可以用雅可比θ函数 Jacobi theta function[math]\displaystyle{ \vartheta_{01}(z=0;\tau=2ix^2/\pi) }[/math]表示。在零假设下，Andrey Kolmogorov定义并规范了Kolmogorov–Smirnov检验统计量的形式及其渐近分布，[1]Nikolai Smirnov则规范了分布表。[2]这里可以运用有限样本中检验统计量分布的递归关系。[1]


当样本来自假设分布F(x)的零假设下，


[math]\displaystyle{ \sqrt{n}D_n\xrightarrow{n\to\infty}\sup_t |B(F(t))| }[/math]


在其分布中，[math]\displaystyle{ B(t) }[/math]指的是布朗桥 Brownian bridge。


如果F是连续的，则在原假设 [math]\displaystyle{ \sqrt{n}D_n }[/math]下收敛到不依赖于F的Kolmogorov分布。该结果也称为Kolmogorov定理。当[math]\displaystyle{ n }[/math] 为有限时，此极限的精确度近似为[math]\displaystyle{ K }[/math]的确切累积分布函数，效果并不十分令人满意：即使[math]\displaystyle{ n=1000 }[/math]，相应的最大误差约为[math]\displaystyle{ 0.9\% }[/math]。在[math]\displaystyle{ n=100 }[/math]时，此误差增加到[math]\displaystyle{ 2.6\% }[/math]，在[math]\displaystyle{ n=10 }[/math]时增加到完全不可接受的[math]\displaystyle{ 7\% }[/math]。但是，如果简单地将[math]\displaystyle{ x }[/math]替换为


[math]\displaystyle{ x+\frac{1}{6\sqrt{n}}+ \frac{x-1}{4n} }[/math]


在Jacobi theta函数的参数e中，将这些误差分别减小到[math]\displaystyle{ 0.003\% }[/math], [math]\displaystyle{ 0.027\% }[/math]和[math]\displaystyle{ 0.27\% }[/math]；该精度足以满足现阶段所有实际应用。[3]


拟合优度检验或Kolmogorov–Smirnov检验可通过使用Kolmogorov分布的临界值来构建。当[math]\displaystyle{ n \to\infty }[/math]时，该检验是渐近有效的。如果条件为：


[math]\displaystyle{ \sqrt{n}D_n\gt K_\alpha,\, }[/math]，


它会拒绝[math]\displaystyle{ \alpha }[/math]等级上的零假设。即Kα为：


[math]\displaystyle{ \operatorname{Pr}(K\leq K_\alpha)=1-\alpha.\, }[/math]


这个检验的渐近幂是1。


用于计算任意[math]\displaystyle{ n }[/math]和[math]\displaystyle{ x }[/math]的累积分布函数[math]\displaystyle{ \operatorname{Pr}(D_n \leq x) }[/math]或其补数的快速准确的算法可以从以下获取:

  • 统计软件期刊2011年Journal of Statistical Software刊登的Simard R, L'Ecuyer P的文章《计算双向Kolmogorov–Smirnov分布》[4]以及统计与概率通信期刊2017年刊登的Moscovich A, Nadler B 的文章《快速计算泊松过程的边界穿越概率》。[5]关于连续零分布的C和Java代码实现可以在文章《计算双向Kolmogorov–Smirnov分布》中找到。[4]
  • 统计软件期刊2019年Journal of Statistical Software刊登的Dimitrova DS, Kaishev VK, Tan S的文章《当潜在累积分布函数是完全离散，混合或连续时，计算Kolmogorov–Smirnov分布》[6]和Dimitrova, Dimitrina; Kaishev, Vladimir; Tan, Senren.的文章《KSgeneral：计算（离散）连续零分布的K-S检验的P值》。[7]R工程KSgeneral软件包中实现的纯离散，混合或连续零分布，可以进行统计计算，对于给定的样本，它还可以计算KS检验统计量及其p值。或者，可以从文章《当潜在累积分布函数是完全离散，混合或连续时，计算Kolmogorov–Smirnov分布》中获得替代的C++实现。[6]


用估计的参数进行测试

如果以数据Xi来确定F(x)的形式或参数，则以这种方式确定的临界值是无效的。在这种情况下，可能需要蒙特卡洛 Monte Carlo或其他方法，不过数据表格已经做了多个情况下的准备。业界目前已经发布了对测试统计量的必要修正细节以及正态分布和指数分布临界值的具体信息，[8]以后的出版物还包括耿贝尔 Gumbel分布。[9]另外莉莉福斯 Lilliefors检验代表正态分布的一种特殊情况。另外为了克服Kolmogorov检验数据可能不符合来自正态分布假设的情况，可以进行对数变换。


想要使用估计参数值，自然而然会出现应该使用哪种估计方法的问题。通常情况下，采用的是最大似然法，但对于如正态分布，最大似然法在sigma上具有较大的偏差。而使用矩量拟合或KS最小化来替代则对临界值有很大影响，并且对检验功效也有一定影响。如果我们需要通过KS测试来确定df = 2的Student-T数据是否正常，那么基于H0</sub的最大似然率估计（数据是正常的，因此使用标度的标准偏差）会得出更大的KS距离，从而不符合最小KS的拟合。在这种情况下，我们应该拒绝H0</sub，在最大似然法中通常是这样，因为对于T-2数据而言，样本标准偏差可能非常大，但是如果将KS最小化，我们可能会得到太低的KS而无法拒绝H0。在Student-T情况下，用KS估计而不是最大似然法来进行改进的KS检验会使其效果稍差一些。但是在其他情况下，经过改良的KS检测会得到更好的检验功效。


离散和混合零分布

假设[math]\displaystyle{ F(x) }[/math]是非递减且右连续的，且具有可数（可能是无限）的跳变次数，则KS检验统计量可表示为：


[math]\displaystyle{ D_n= \sup_x |F_n(x)-F(x)| = \sup_{0 \leq t \leq 1} |F_n(F^{-1}(t)) - F(F^{-1}(t))|. }[/math]


从[math]\displaystyle{ F(x) }[/math]的右连续性，可以得出[math]\displaystyle{ F(F^{-1}(t)) \geq t }[/math]和[math]\displaystyle{ F^{-1}(F(x)) \leq x }[/math]，因此[math]\displaystyle{ D_{n} }[/math]的分布取决于零分布[math]\displaystyle{ F(x) }[/math]，即在连续情况下不再无分布。目前已经开发出一种快速，准确的方法，以C ++和R语言的KSgeneral软件包来实现，当[math]\displaystyle{ F(x) }[/math]是纯离散或混合时，可以计算出Dn的精确且渐近分布。函数disc_ks_test()，mixed_ks_test()和cont_ks_test()还可以针对纯离散，混合或连续的零分布和任意样本大小，计算出KS检测统计量和p值。[10]另外作为R语言的dgof软件包的一部分，还可以计算出KS检测及其用于离散零分布和小样本量的p值。关于主要统计软件包，其中SAS PROC NPAR1WAY[11]和Stata ksmirnov [12]是假设[math]\displaystyle{ F(x) }[/math]是连续的，因此执行KS检验时，如果零分布实际上不是连续的，则该检验更为保守。详情请见：

  1. 《关于离散案例中的Kolmogorov统计量的注释 Note on the Kolmogorov Statistic in the Discrete Case》[13]
  2. 《皮尔逊卡方检验和Kolmogorov拟合优度检验在有效性方面的比较 A Comparison of the Pearson Chi-Square and Kolmogorov Goodness-of-Fit Tests with Respect to Validity》[14]
  3. 《Kolmogorov–Smirnov的有限概率性质和离散数据的相似统计量 Bounded Probability Properties of Kolmogorov–Smirnov and Similar Statistics for Discrete Data》[15]

Two-sample Kolmogorov–Smirnov test 双样本Kolmogorov–Smirnov检验

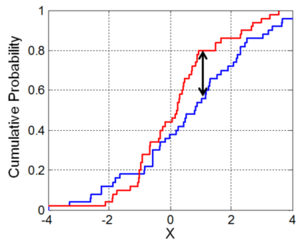
关于两个样本的Kolmogorov–Smirnov统计量的图解。 红线和蓝线分别对应于经验分布函数，而黑色箭头是两样本的KS统计量。

Kolmogorov–Smirnov检验也可用于检验两个潜在的一维概率分布是否不同。在这种情况下，Kolmogorov-Smirnov统计量为


[math]\displaystyle{ D_{n,m}=\sup_x |F_{1,n}(x)-F_{2,m}(x)|, }[/math]


其中[math]\displaystyle{ F_{1,n} }[/math]和[math]\displaystyle{ F_{2,m} }[/math]分别是第一样本和第二样本的经验分布函数，而[math]\displaystyle{ \sup }[/math]是上确界函数。


对于量大的样本，如果满足以下条件，则原假设在[math]\displaystyle{ \alpha }[/math]级被拒绝


[math]\displaystyle{ D_{n,m}\gt c(\alpha)\sqrt{\frac{n + m}{n\cdot m}}. }[/math]


其中[math]\displaystyle{ n }[/math]和[math]\displaystyle{ m }[/math]分别是第一样本和第二样本的大小。下表给出了在[math]\displaystyle{ \alpha }[/math]级最常见的[math]\displaystyle{ c({\alpha}) }[/math]值：


| [math]\displaystyle{ \alpha }[/math] || 0.20 || 0.15 || 0.10 || 0.05 || 0.025 || 0.01 || 0.005 || 0.001

|-

| [math]\displaystyle{ c({\alpha}) }[/math] || 1.073 || 1.138 || 1.224 || 1.358 || 1.48 || 1.628 || 1.731 || 1.949

|}

一般而言：


[math]\displaystyle{ c\left(\alpha\right)=\sqrt{-\ln\left(\tfrac{\alpha}{2}\right)\cdot \tfrac{1}{2}}, }[/math]


以至于条件为：


[math]\displaystyle{ D_{n,m}\gt \frac{1}{\sqrt{n}}\cdot\sqrt{-\ln\left(\tfrac{\alpha}{2}\right)\cdot \tfrac{1 + \tfrac{n}{m}}{2}}. }[/math]


同样，样本量越大，最小界限越敏感：对于给定比率的样本大小（例如m = n），最小界限根据其平方根的倒数来缩放两个样本的大小。


这里要注意的是两个样本检验出来的数据样本是否来自同一分布。其并未指定该共同分布是什么（例如，它是正常还是不正常）。而且关键值表已经得出。Kolmogorov–Smirnov检验没有那么有效，因为它被设计为对两个分布函数之间所有可能的差异敏感。如刊登在Journal of Nonparametric Statistics2009年刊上Marozzi, Marco (2009)的文章《Some Notes on the Location-Scale Cucconi Test》和刊登在Communications in Statistics – Simulation and Computation2013年刊上同样Marozzi, Marco (2009)的文章《Nonparametric Simultaneous Tests for Location and Scale Testing: a Comparison of Several Methods显示了证据，当比较两个分布函数时，最初建议同时比较位置和比例的Cucconi检验比Kolmogorov-Smirnov检验更有效。


为分布函数的形状设置置信极限

While the Kolmogorov–Smirnov test is usually used to test whether a given F(x) is the underlying probability distribution of Fn(x), the procedure may be inverted to give confidence limits on F(x) itself. If one chooses a critical value of the test statistic Dα such that P(Dn > Dα) = α, then a band of width ±Dα around Fn(x) will entirely contain F(x) with probability 1 − α.


虽然通常使用Kolmogorov–Smirnov检验法来检验给定的F(x)是否为Fn(x)的潜在概率分布，但可以将过程倒过来给出F(x)本身的置信极限。如果选择检验统计量Dα) = α的临界值，使得 P(Dn，则在Fn(x) 周围宽度±Dα内将完全包含概率为1-α的F(x) 。


The Kolmogorov–Smirnov statistic in more than one dimension 多个维度的Kolmogorov–Smirnov统计

朱斯特尔 Justel，培尼亚 Peña和扎马 Zamar（1997）提出了无分布的多元Kolmogorov-Smirnov拟合优度检验。该检验使用通过Rosenblatt变换建立的统计量，开发出了一种算法来计算双变量情况。还介绍了可以在任何维度上轻松计算的近似检测法。


如果要将类似的检验应用于多元数据，则需要修改Kolmogorov–Smirnov检验统计量。过程略显复杂，因为两个联合累积分布函数之间的最大差异通常与任何互补分布函数中的最大差异都不相同。因此，最大差异将取决于使用[math]\displaystyle{ \Pr(x \lt X \land y \lt Y) }[/math]或[math]\displaystyle{ \Pr(X \lt x \land Y \gt y) }[/math]中的哪一个，或者使用其他两种可能分布中的任何一种。当然有可能要求所用的检测结果无关于这样的选择。


在满足以上要求的同时，将Kolmogorov-Smirnov统计量泛化为更高维度的一种方法是，在所有可能的排序中比较两个样本的累积分布函数，并从所得的K-S统计量中取最大。在d 维数据中，有 2d−1个这样的排序。皮柯克 Peacock得出了一种这样的变化量（有关3D版本，另请参见Gosset），另一种由法萨诺 Fasano和弗朗切斯基尼 Franceschini得出（有关比较和计算细节，请参见Lopes等人）。检测统计量的临界值可以通过仿真获取，但取决于联合分布中的依存关系结构。


一维的Kolmogorov-Smirnov统计量与所谓的星差D相同，因此，另一个对更高维度的本地KS扩展是将D也用于更高维度。可惜的是，很难从高维度上计算出星差。


Implementations 软件实现

Kolmogorov-Smirnov检验（一个或两个抽样检验可验证分布是否相等）可以在众多软件程序中实现：

  • 科学计算软件 Wolfram Mathematica内含KolmogorovSmirnovTestt。
  • MATLAB在其统计工具箱中含有kstest。
  • R语言包“KSgeneral”[7] 可以在任意，可能离散，混合或连续的零分布下计算KS检验统计信息及其p值。
  • R语言的统计基本程序包在其“stats”程序包中可以运行检验，命令为ks.test {stats}。
  • 统计软件SAS在其PROC NPAR1WAY程序中可以实现检验。
  • Python通过SciPy[16]中的统计功能（scipy.stats）可以实现检验。
  • SYSTAT（SPSS Inc.，伊利诺伊州芝加哥）
  • 基于Java语言开发的Apache Commons可以实现检验。[17]
  • KNIME是一个数据分析平台，基于上述Java语言，可以通过一个节点Node来实现检验。
  • StatsDirect（StatsDirect Ltd，英国曼彻斯特）包含所有常见的变体。all common variants
  • Stata（德克萨斯州大学城Stata公司）在ksmirnov（Kolmogorov–Smirnov分配均等测试）中执行检验命令。[18]
  • PSPP通过其Kolmogorov–Smirnov（或使用K-S快捷功能）实施检验。KOLMOGOROV-SMIRNOV (or using K-S shortcut
  • Excel以KSCRIT和KSPROB的形式运行检验。


参见


参考文献

  1. ↑ 1.0 1.1 Kolmogorov A (1933). "Sulla determinazione empirica di una legge di distribuzione". G. Ist. Ital. Attuari. 4: 83–91.
  2. ↑ Smirnov N (1948). "Table for estimating the goodness of fit of empirical distributions". Annals of Mathematical Statistics. 19 (2): 279–281. doi:10.1214/aoms/1177730256.
  3. ↑ Vrbik, Jan (2018). "Small-Sample Corrections to Kolmogorov–Smirnov Test Statistic". Pioneer Journal of Theoretical and Applied Statistics. 15 (1–2): 15–23.
  4. ↑ 4.0 4.1 Simard R, L'Ecuyer P (2011). "Computing the Two-Sided Kolmogorov–Smirnov Distribution". Journal of Statistical Software. 39 (11): 1–18. doi:10.18637/jss.v039.i11.
  5. ↑ Moscovich A, Nadler B (2017). "Fast calculation of boundary crossing probabilities for Poisson processes". Statistics and Probability Letters. 123: 177–182. arXiv:1503.04363. doi:10.1016/j.spl.2016.11.027.
  6. ↑ 6.0 6.1 Dimitrova DS, Kaishev VK, Tan S (2019). "Computing the Kolmogorov–Smirnov Distribution when the Underlying cdf is Purely Discrete, Mixed or Continuous". Journal of Statistical Software. forthcoming.
  7. ↑ 7.0 7.1 Dimitrova, Dimitrina; Kaishev, Vladimir; Tan, Senren. "KSgeneral: Computing P-Values of the K-S Test for (Dis)Continuous Null Distribution". cran.r-project.org/web/packages/KSgeneral/index.html.
  8. ↑ Pearson, E. S., ed. (1972). Biometrika Tables for Statisticians. 2. Cambridge University Press. pp. 117–123, Tables 54, 55. ISBN 978-0-521-06937-3. 
  9. ↑ Shorack, Galen R.; Wellner, Jon A. (1986). Empirical Processes with Applications to Statistics. Wiley. p. 239. ISBN 978-0471867258. 
  10. ↑ Arnold, Taylor B.; Emerson, John W. (2011). "Nonparametric Goodness-of-Fit Tests for Discrete Null Distributions" (PDF). The R Journal. 3 (2): 34\[Dash]39. doi:10.32614/rj-2011-016.
  11. ↑ "SAS/STAT(R) 14.1 User's Guide". support.sas.com. Retrieved 14 April 2018.
  12. ↑ "ksmirnov — Kolmogorov–Smirnov equality-of-distributions test" (PDF). stata.com. Retrieved 14 April 2018.
  13. ↑ Noether GE (1963). "Note on the Kolmogorov Statistic in the Discrete Case". Metrika. 7 (1): 115–116. doi:10.1007/bf02613966.
  14. ↑ Slakter MJ (1965). "A Comparison of the Pearson Chi-Square and Kolmogorov Goodness-of-Fit Tests with Respect to Validity". Journal of the American Statistical Association. 60 (311): 854–858. doi:10.2307/2283251. JSTOR 2283251.
  15. ↑ Walsh JE (1963). "Bounded Probability Properties of Kolmogorov–Smirnov and Similar Statistics for Discrete Data". Annals of the Institute of Statistical Mathematics. 15 (1): 153–158. doi:10.1007/bf02865912.
  16. ↑ "scipy.stats.kstest". SciPy SciPy v0.14.0 Reference Guide. The Scipy community. Retrieved 18 June 2019.
  17. ↑ "KolmogorovSmirnovTes". Retrieved 18 June 2019.
  18. ↑ "ksmirnov — Kolmogorov –Smirnov equality-of-distributions test" (PDF). Retrieved 18 June 2019.


进一步阅读

  • Daniel, Wayne W. (1990). "Kolmogorov–Smirnov one-sample test". Applied Nonparametric Statistics (2nd ed.). Boston: PWS-Kent. pp. 319–330. ISBN 978-0-534-91976-4.
  • Eadie, W.T.; D. Drijard; F.E. James; M. Roos; B. Sadoulet (1971). Statistical Methods in Experimental Physics. Amsterdam: North-Holland. pp. 269–271. ISBN 978-0-444-10117-4.
  • Stuart, Alan; Ord, Keith; Arnold, Steven [F.] (1999). Classical Inference and the Linear Model. Kendall's Advanced Theory of Statistics. 2A (Sixth ed.). London: Arnold. pp. 25.37–25.43. ISBN 978-0-340-66230-4. MR 1687411.
  • Corder, G. W.; Foreman, D. I. (2014). Nonparametric Statistics: A Step-by-Step Approach. Wiley. ISBN 978-1118840313.
  • Stephens, M. A. (1979). "Test of fit for the logistic distribution based on the empirical distribution function". Biometrika. 66 (3): 591–595. doi:10.1093/biomet/66.3.591.


  • Daniel, Wayne W. (1990). " Kolmogorov–Smirnov单样本检验. Applied Nonparametric Statistics (2nd ed.). Boston: PWS-Kent. pp. 319–330. ISBN 978-0-534-91976-4.
  • Eadie, W.T.; D. Drijard; F.E. James; M. Roos; B. Sadoulet (1971). 实验物理中的统计方法. Amsterdam: North-Holland. pp. 269–271. ISBN 978-0-444-10117-4.
  • Stuart, Alan; Ord, Keith; Arnold, Steven [F.] (1999). 经典推论和线性模型。肯德尔Kendall高级统计理论. 2A (Sixth ed.). London: Arnold. pp. 25.37–25.43. ISBN 978-0-340-66230-4. MR 1687411.
  • Corder, G. W.; Foreman, D. I. (2014). 非参数统计：分步法. Wiley. ISBN 978-1118840313.
  • Stephens, M. A. (1979). "基于经验分布函数的逻辑分布拟合检验". Biometrika. 66 (3): 591–595. doi:10.1093/biomet/66.3.591.
取自“https://wiki.swarma.org/index.php?title=KS检验&oldid=21652”