概率图模型

图模型 Graphical Model，亦称概率图模型 Probabilistic Graphical Model（PGM）或结构化概率模型 structured probabilistic model，是一种用图表示随机变量之间条件依赖关系的概率模型。它们通常用于概率论、统计学，尤其是贝叶斯统计学和机器学习。

这是一个图模型的例子。每个箭头表示一个依赖关系。在这个例子中: D 依赖于 A、 B 和 C; C 依赖于 B 和 D; 而 A 和 B 相互独立。

常用的概率图模型大致分为两类：贝叶斯网络（Bayesian network, BN）和马尔可夫网络（Markovnetwork, MN）或者称为马尔可夫随机场。概率图理论共分为三个部分，分别为概率图模型表示理论，概率图模型推理理论和概率图模型学习理论。

其中：

• 图模型的表示representation是指：如何用图模型来将概率分布进行表示；
• 图模型的推理inference是指：在已知图模型的情况下，如何计算某一未知节点的概率；
• 图模型的学习learning是指：对图的结构和参数的学习。

图模型的表示

一般来说，概率图模型中图的表示方法常常作为对多维空间上的分布进行编码的基础，主要由参数和结构两个部分组成。

常用的概率图模型大致分为两类：贝叶斯网络（Bayesian network, BN）和马尔可夫网络（Markov network, MN）或者称为马尔可夫随机场（Markov Random Field, MRF）。这两种模型的主要思想都是利用条件独立性假设来对联合概率分布进行因式分解，从而达到降维的目的。 概率图模型的好处是提供了一种简单的可视化概率模型的方法，有利于设计和开发新模型，并且简化数学表示，提高推理运算能力。

贝叶斯网络一般是指有向图模型，使用有向无环图来表示变量之间的关系；

马尔可夫随机场一般是指在无向图模型，使用无向图来表示变量之间的关系。

贝叶斯网络

如果模型的网络结构是有向无环图，则模型表示所有随机变量的联合概率的因式分解。更确切地说，如果事件是[math]\displaystyle{ X_1,\ldots,X_n }[/math]，那么联合概率满足：

[math]\displaystyle{ P[X_1,\ldots,X_n]=\prod_{i=1}^nP[X_i|\text{pa}(X_i)] }[/math]

其中 [math]\displaystyle{ \text{pa}(X_i) }[/math] 是节点 [math]\displaystyle{ X_i }[/math] 的父节点集（节点的边际指向 [math]\displaystyle{ X_i }[/math] )。换句话说，联合分布因子可以表示为条件分布的乘积。例如，上图中的图模型（实际上不是有向无环图，而是原始图）是由随机变量[math]\displaystyle{ A, B, C, D }[/math] 组成，联合概率密度因子为

[math]\displaystyle{ P[A,B,C,D] = P[A]\cdot P[B]\cdot P[C,D|A,B] }[/math]

任何两个节点都是和其父节点的值是条件独立的。一般来说，如果 d-分离准则在图中成立，那么任意两组节点和给定第三个节点集都是条件独立的。在贝叶斯网络中，局部独立性和全局独立性是等价的。

这种类型的图形模型被称为有向图模型、贝氏网路或信念网络。经典的机器学习模型：隐马尔可夫模型、神经网络和更新的模型如可变阶马尔可夫模型都可以看作是贝叶斯网络的特殊情况。

马尔可夫随机场

如果模型的网络结构是无向图，则模型表示所有团的联合概率的因式分解。更确切地说，如果[math]\displaystyle{ x_{ \{ k \}} }[/math]是随机变量[math]\displaystyle{ x }[/math]在第k个团的状态（[math]\displaystyle{ |c_k| }[/math]是在第k个团中包含的节点数），那么联合概率满足：

[math]\displaystyle{ P(X=x) = \frac{1}{Z} \prod_{k} f_k (x_{ \{ k \}}) }[/math]

其中[math]\displaystyle{ Z }[/math]是配分函数，有

[math]\displaystyle{ Z = \sum_{x \isin \mathcal{X}} \prod_{k} f_k(x_{ \{ k \} }) }[/math].

实际上，马尔可夫随机场经常表示为对数线性模型。通过引入特征函数[math]\displaystyle{ \phi_k }[/math]，得到

[math]\displaystyle{ f_k=\exp \left(w_k^{\top} \phi_k (x_{ \{ k \}}) \right) }[/math]

和

[math]\displaystyle{ P(X=x) = \frac{1}{Z} \exp \left( \sum_{k} w_k^{\top} \phi_k (x_{ \{ k \}}) \right) }[/math]

以及配分函数

[math]\displaystyle{ Z = \sum_{x \isin \mathcal{X}} \exp \left(\sum_{k} w_k^{\top}\phi_k(x_{ \{ k \} })\right) }[/math]。

其中，[math]\displaystyle{ w_k }[/math]是权重，[math]\displaystyle{ \phi_k }[/math]是势函数，映射团[math]\displaystyle{ k }[/math]到实数。

图模型的推理

概率图模型的推理方法主要分精确推理和近似推理两大类，而根据网络结构和查询问题的不同，概率图模型的推理方法可以分为三大类，分别是BN和MN的推理、混合网络的推理和DBN的推理，然后再根据查询问题的形式对每一类推理方法继续细分，下图着重介绍BN和MN的推理。

BN和 MN的推理算法分类

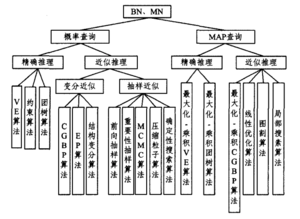
其中概率查询是计算后验概率分布[math]\displaystyle{ P(Y|E=e) }[/math]，其中[math]\displaystyle{ Y }[/math]是查询变量集，[math]\displaystyle{ E }[/math]为证据变量集；MAP表示最大后验概率查询，也称最有可能解释查询，即求出非证据变量集的最有可能取值。

图模型的学习

由于概率图模型的表示分参数表示和结构表示两个部分, 因此学习算法也分为参数学习与结构学习两大类。

贝叶斯网络模型学习

贝叶斯网络模型模型的参数学习，一般会假设结构一致，然后从样本数据中学习每个变量的概率分布。概率分布的形式一般会预先设定，如多项式分布、高斯分布和泊松分布等。 贝叶斯网络模型的结构学习是贝叶斯网络学习的最主要的部分，此时贝叶斯网络的参数和结构都未知，需要从样本数据中找到与数据匹配度最好的网络结构。当确定网络结构之后，参数学习知识相对简单的参数估计问题。结构学习的算法主要分为三类：基于约束 (Constraint based, CB) 的学习算法、基于评分搜索(Scoring and searching, SS) 的学习算法和混合学习算法。

马尔可夫随机场模型学习

马尔可夫随机场模型的学习任务比贝叶斯网络模型的学习更加复杂。在马尔可夫随机场模型的参数学习中, 其配分函数耦合了结构中的所有参数，使得参数学习问题不能分解，不能分别独立估计每个局部参数。 而且马尔可夫随机场的最优参数没有解析解，所以一般使用迭代方法求解最优参数，如梯度下降法。庆幸的是，迭代中的似然目标函数为凹函数，迭代方法能保证收敛至全局最优解。但是迭代中的每一步都需要在网络中进行推理，使得计算成本相当高。MN 的结构学习也需要计算划分函数，所以其参数学习存在的问题对结构学习有很大的影响。

其他类别

• 朴素贝叶斯分类器 Naive Bayes classifier，其中会使用单根树。
• 依赖性网络 Dependency network中会出现环。
• 树增广朴素贝叶斯分类器 Tree-augmented classifier 或简称为TAN模型。
• 因子图 factor graph是连接变量和因子的无向二分图。 每个因子代表与其连接的变量有关的函数。 这对于理解和实现信念传播算法很有帮助。
• 团树 clique tree或者联合树，是指基于团的树，一般是将有向图转化为树，减少计算难度，一般会使用联合树算法来求解。
• 链式图 chain graph 是既可以有向也可以无向的边，但是没有任何有向环（即，如果我们从任意一个顶点开始并依据任何箭头的方向沿该图形移动，则只要我们沿着箭头走了一步我们将无法返回到该顶点）。 有向无环图和无向图都是链式图的特例，因此可以提供一种统一和泛化贝叶斯网络和马尔可夫网络的方法。

• 祖先图是既有有向边，也有双向边和无向边的图。

• 随机场方法

• • 马尔可夫随机场也称为马尔可夫网络，是一个基于无向图的模型，图模型中很多重复的子单元可以用 “盘子表示法”（plate notation） 来进行表示。

• • 条件随机场是基于无向图上的判别模型。

• 受限玻尔兹曼机是一个基于无向图上的二分生成模型。

应用

该模型的框架为发现和分析复杂分布中的结构、简洁地描述结构和提取非结构化信息提供了算法，使模型得到有效的构建和利用。图形模型的应用包括因果推理、信息抽取、语音识别、l计算机视觉、低密度奇偶校验码的解码、基因调控网络的建模、基因发现和疾病诊断，以及蛋白质结构的图形模型。

另见

• Belief propagation 信念传递网络
• Structural equation model 结构方程模型

进一步阅读

书籍

• Barber, David (2012). Bayesian Reasoning and Machine Learning. Cambridge University Press. ISBN 978-0-521-51814-7. 
• Bishop, Christopher M. (2006). "Chapter 8. Graphical Models". Pattern Recognition and Machine Learning. Springer. pp. 359–422. ISBN 978-0-387-31073-2. MR 2247587. https://www.microsoft.com/en-us/research/wp-content/uploads/2016/05/Bishop-PRML-sample.pdf. 
• Cowell, Robert G.; Dawid, A. Philip; Lauritzen, Steffen L. author4=Spiegelhalter, David J. (1999). Probabilistic networks and expert systems. Berlin: Springer. ISBN 978-0-387-98767-5. MR 1697175.  一本更先进和面向统计的书。
• Jensen, Finn (1996). An introduction to Bayesian networks. Berlin: Springer. ISBN 978-0-387-91502-9. 
• Pearl, Judea (1988). Probabilistic Reasoning in Intelligent Systems (2nd revised ed.). San Mateo, CA: Morgan Kaufmann. ISBN 978-1-55860-479-7. MR 0965765. 一种计算推理方法，图和概率之间的关系被正式引入。

论文

• Edoardo M. Airoldi (2007). "Getting Started in Probabilistic Graphical Models". PLoS Computational Biology. 3 (12): e252. doi:10.1371/journal.pcbi.0030252. PMC 2134967. PMID 18069887.
• Jordan, M. I. (2004). "Graphical Models". Statistical Science. 19: 140–155. doi:10.1214/088342304000000026.
• Ghahramani, Zoubin (May 2015). "Probabilistic machine learning and artificial intelligence". Nature (in English). 521 (7553): 452–459. doi:10.1038/nature14541. PMID 26017444.

其他

• Heckerman's Bayes Net Learning Tutorial

• A Brief Introduction to Graphical Models and Bayesian Networks

• Sargur Srihari's lecture slides on probabilistic graphical models

其他链接

• Graphical models and Conditional Random Fields
• Probabilistic Graphical Models taught by Eric Xing at CMU

编者推荐

课程推荐

概率图模型

人工智能可以看做两个割裂的阶段，一是早期的基于符号的搜索，二是现在的机器学习，概率图模型可以将两者统一起来。概率图模型完美融合了人工智能的各个任务，我们既可以表示知识、推理、概率推断、learning，是为数不多的能够统一全部内容的方法。本课程中，北京师范大学系统科学学院教授张江将从概率理论、贝叶斯网、马尔科夫网和表示学习四部分内容讲解概率图模型。

概率上的图模型|Openlab内部读书会第一期分享

这部分内容是由北京师范大学的张章进行分享的内容，也可以作为一个参考推荐给大家。

因果科学与Causal AI读书会第二季

因果科学读书会的第二季将会从基础的部分介绍图模型，以及更多跟图模型拓展相关，解释因果性的文章。读书会期间将会精读三本因果科学方向的优秀书籍，并共同完成书籍中的思考题。

因果科学与Causal AI读书会第二季

---

本中文词条由HaoZHAN翻译，Yuling审校，薄荷欢迎在讨论页面留言。

本词条内容源自公开资料，遵守 CC3.0协议。