分层随机试验

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
孙钦贵（讨论 | 贡献）2021年6月11日 (五) 19:59的版本 （→‎Disadvantage）
跳到导航 跳到搜索
分层随机抽样的图形分解 Graphic breakdown of stratified random sampling

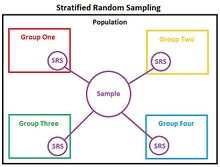
在统计学中， 分层随机试验 Stratified randomization 是一种抽样方法，首先将整个研究 总体 Population 层为具有相同属性或特征的子群，称为 分层 Attributes ，然后从分层组中进行简单随机抽样，在抽样过程的任何阶段，随机、完全偶然地无偏抽取同一子群中的元素。[1][2]分层随机试验被认为是 分层抽样 Stratified sampling 的一个细分。当共享属性部分存在，并且在被调查总体的不同亚群之间有很大差异时，应该采用分层随机试验。因此，在取样过程中需要特别考虑或明确区分。[3]这种抽样方法应区别于 整群抽样方法 Cluster sampling ，整群抽样方法是在整个群体中选择一个简单的随机抽样来代表整个总体，或分层系统抽样方法，在分层过程之后进行 系统抽样 Systematic sampling 。分层随机抽样有时也称为 定额随机抽样 Quota random sampling 。[1]


分层随机试验的步骤

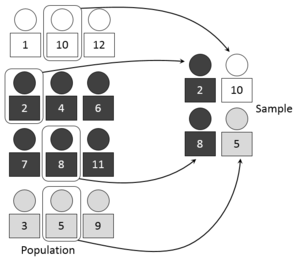
分层随机试验在目标总体异 质性 Heterogeneous的情况下非常有用， 它能有效地显示研究中的趋势或特征在不同阶层之间的差异。[1]当进行分层随机试验时，应采取以下8个步骤：[4][5]

  1. 定义目标总体
  2. 定义分层 变量 Variables 并决定要创建的分层数量。确定分层变量的标准,包括年龄、社会经济地位、国籍、种族、教育程度等，并应与研究目标相一致。理想情况下，应该使用4-6个阶层，因为任何分层变量的增加将提高其中一些变量抵消其他变量的影响的概率。[5]
  3. 使用 抽样框架 Sampling frame 评估目标总体中的所有元素。之后根据 覆盖率 Coverage 和分组进行更改。
  4. 列出所有的元素并考虑抽样结果。每个阶层应该相互排斥 Mutually exclusive，加起来涵盖总体的所有成员，而总体的每一个成员应该属于唯一的阶层，和其他差异最小的成员一起。[4]
  5. 决定随机抽样的选择标准。这可以手动完成，也可以用设计好的计算机程序完成。
  6. 为所有元素分配一个随机且唯一的编号，然后根据分配的编号对这些元素进行排序。
  7. 回顾每一层的大小（Size）和每一层中所有元素的 数值分布 Numerical distribution 。确定抽样类型，按比例或不按比例分层抽样。
  8. 按照第5步中的规定进行所选的随机抽样。至少，必须从每个阶层中选择一种元素，以便最终样品包括每个阶层的代表。如果从每个阶层中选择两个或两个以上的元素，则可以计算所收集数据的 误差范围 Error margins 。[5]


Simple randomization is considered as the easiest method for allocating subjects in each stratum. Subjects are assigned to each group purely randomly for every assignment. Even though it is easy to conduct, simple randomization is commonly applied in strata that contain more than 100 samples since a small sampling size would make assignment unequal.

简单随机化被认为是最简单的方法分配主体在每个阶层。每次分配的主题都是随机分配给每个小组的。尽管简单的随机化方法易于实施，但是由于小样本容易造成分配不等，因此在样本数超过100个的地层中常常采用简单的随机化方法。

Techniques

分层后简单随机抽样

Stratified randomization decides one or multiple prognostic factors to make subgroups, on average, have similar entry characteristics. The patient factor can be accurately decided by examining the outcome in previous studies.[6]

分层随机试验决定一个或多个预后因素，使亚组平均具有相似的进入特征。Stratified randomization decides one or multiple prognostic factors to make subgroups, on average, have similar entry characteristics. 通过检查先前研究的结果，可以准确地确定患者因素。[7]

The number of subgroups can be calculated by multiplying the number of strata for each factor.  Factors are measured before or at the time of randomization and experimental subjects are divided into several subgroups or strata according to the results of measurements.[8] 子群的数量可以通过乘以每个因素的层数来计算。在随机化前或随机化时测量因素，并根据测量结果将实验对象分为若干亚组或层。

Within each stratum, several randomization strategies can be applied, which involves simple randomization, blocked randomization, and minimization.

在每一层中，可以应用几种随机试验策略，包括 简单随机试验 Simple randomization 、 分块随机试验 Blocked randomization 和 最小化试验 Minimization 。

Simple randomization within strata

Simple randomization is considered as the easiest method for allocating subjects in each stratum. Subjects are assigned to each group purely randomly for every assignment. Even though it is easy to conduct, simple randomization is commonly applied in strata that contain more than 100 samples since a small sampling size would make assignment unequal.[8]

简单随机试验被认为是在每个阶层中分配受试者的最简单方法。对于每个任务，受试者被完全随机地分配到每个组中。尽管简单的随机化很容易进行，但由于取样量小，分配不均，因此在含有100多个样本的地层中，通常采用简单的随机化方法。尽管很容易进行，但简单随机试验通常应用于包含 100 个以上样本的层，因为小样本量会使分配不均等。

分层内的区块随机试验 Block randomization within strata

Block randomization, sometimes called permuted block randomization, applies blocks to allocate subjects from the same strata equally to each group in the study. In block randomization, allocation ratio (ratio of the number of one specific group over other groups) and group sizes are specified. The block size must be the multiples of the number of treatments so that samples in each stratum can be assigned to treatment groups with the intended ratio.[8] For instance, there should be 4 or 8 strata in a clinical trial concerning breast cancer where age and nodal statuses are two prognostic factors and each factor is split into two-level. The different blocks can be assigned to samples in multiple ways including random list and computer programming.[9][10]

区块随机试验 Block randomization ，有时称为置换区块随机试验，应用区块将来自同一阶层的受试者平均分配到研究中的每个组。 在区块随机试验中，指定了分配比率（一个特定组与其他组的数量之比）和组大小。 块大小必须是处理次数的倍数，以便每个层中的样本可以按预期比例分配到处理组。[8]例如，在一项关于乳腺癌的临床试验中，应该有 4 或 8 个层次，其中年龄和淋巴结状态是两个预后因素（prognostic factors），每个因素分为两个水平。 可以通过多种方式将不同的区块分配给样本，包括随机列表（random list）和计算机编程。

Block randomization is commonly used in the experiment with a relatively big sampling size to avoid the imbalance allocation of samples with important characteristics. In certain fields with strict requests of randomization such as clinical trials, the allocation would be predictable when there is no blinding process for conductors and the block size is limited. The blocks permuted randomization in strata could possibly cause an imbalance of samples among strata as the number of strata increases and the sample size is limited, For instance, there is a possibility that no sample is found meeting the characteristic of certain strata.

区块随机试验通常用于样本量较大的实验，以避免具有重要特征的样本分配不平衡。 在某些对随机试验有严格要求的领域，如临床试验，当没有对导体（conductors）进行盲法处理且区块块大小有限时，分配是可预测的。 分层中的块置换随机试验可能会随着分层数量的增加和样本量的限制而导致分层之间的样本不平衡，例如，有可能找不到符合某些分层特征的样本[11]。

最小化方法 Minimization method

In order to guarantee the similarity of each treatment group, the "minimization" method attempts are made, which is more direct than random permuted block within strats. In the minimization method, samples in each stratum are assigned to treatment groups based on the sum of samples in each treatment group, which makes the number of subjects keep balance among the group.[8] If the sums for multiple treatment groups are the same, simple randomization would be conducted to assign the treatment. In practice, the minimization method needs to follow a daily record of treatment assignments by prognostic factors, which can be done effectively by using a set of index cards to record.  The minimization method effectively avoids imbalance among groups but involves less random process than block randomization because the random process is only conducted when the treatment sums are the same. A feasible solution is to apply an additional random list which makes the treatment groups with a smaller sum of marginal totals possess a higher chance (e.g.¾) while other treatments have a lower chance(e.g.¼ ).[12] 为了保证每个处理组的相似性，尝试了“最小化”方法，这比分层内的随机排列块更直接。在最小化方法中，根据每个处理组中的样本总和将每个层中的样本分配到处理组中，这使得受试者数量在组间保持平衡。[8] 如果多个治疗组的总和相同，则将进行简单的随机化以分配治疗。在实践中，最小化方法需要根据预后因素（prognostic factors）跟踪治疗分配的每日记录，这可以通过使用一组索引卡进行记录来有效完成。最小化方法有效地避免了组间不平衡，但比块随机化涉及的随机过程更少，因为随机过程仅在治疗的总人数相同时进行。一个可行的解决方案是应用额外的随机列表，这使得具有较小边际总数的总和的治疗组具有更高的机会（例如 ¾），而其他治疗具有较低的机会（例如 ¼）。[12]


In order to guarantee the similarity of each treatment group, the "minimization" method attempts are made, which is more direct than random permuted block within strats. In the minimization method, samples in each stratum are assigned to treatment groups based on the sum of samples in each treatment group, which makes the number of subjects keep balance among the group.

为了保证每个处理组之间的相似性，尝试了“最小化”方法，这种方法比层内随机置乱更直接。在最小化方法中，根据每个处理组的样本总和，将每个地层的样本分配给处理组，使处理组的受试者人数保持平衡。

为了避免重要特征样本分配不平衡的问题，实验中常采用分块随机化的方法，采样规模较大。在某些严格要求随机化的领域，例如临床试验，当没有导体的盲法和块大小有限时，分配是可以预测的。随着地层数量的增加和样本容量的限制，地层中的块体随机化可能导致地层之间样本的不平衡，例如，有可能找不到符合特定地层特征的样本。

Stratified random sampling is useful and productive in situations requiring different weightings on specific strata. In this way, the researchers can manipulate the selection mechanisms from each strata to amplify or minimize the desired characteristics in the survey result.

分层随机抽样在特定地层需要不同权重的情况下是有用的和有效的。通过这种方式，研究人员可以操纵来自每个阶层的选择机制，以便在调查结果中放大或减少所需的特征。


Stratified randomization is helpful when researchers intend to seek for associations between two or more strata, as simple random sampling causes a larger chance of unequal representation of target groups. It is also useful when the researchers wish to eliminate confounders in observational studies as stratified random sampling allows the adjustments of covariances and the p-values for more accurate results.

当研究人员试图寻找两个或多个阶层之间的联系时，分层随机化是有帮助的，因为简单的随机抽样会导致目标群体代表性不平等的可能性更大。当研究人员希望在观察研究中消除混杂因素时，这也是有用的，因为分层随机抽样允许调整协方差和 p 值以获得更准确的结果。









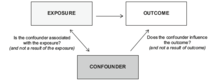
Confounding factors are important to consider in clinical trials

在临床试验中，混杂因素是需要考虑的重要因素


There is also a higher level of statistical accuracy for stratified random sampling compared with simple random sampling, due to the high relevance of elements chosen to represent the population. The step of stratified randomization is extremely important as an attempt to ensure that no bias, delibrate or accidental, affects the representative nature of the patient sample under study. It increases the study power, especially in small clinical trials(n<400), as these known clinical traits stratified are thought to effect the outcomes of the interventions. It helps prevent the occurrence of type I error, which is valued highly in clinical studies. It also has an important effect on sample size for active control equivalence trials and in theory, facilitates subgroup analysis and interim analysis.

与简单随机抽样相比，分层随机抽样具有更高的统计准确性，因为所选择的元素代表总体具有高度的相关性。分层随机化的步骤是非常重要的，它试图确保没有偏差，取样或偶然，影响研究中患者样本的代表性。它增加了研究力量，特别是在小型临床试验(n < 400) ，因为这些已知的临床特征分层被认为影响干预的结果。它有助于防止 i 型错误的发生，这在临床研究中是很有价值的。它还对主动控制等效试验的样本容量有重要影响，并在理论上简化了亚组分析和中期分析。 


The subgroup size is taken to be of the same importance if the data available cannot represent overall subgroup population. In some applications, subgroup size is decided with reference to the amount of data available instead of scaling sample sizes to subgroup size, which would introduce bias in the effects of factors.  In some cases that data needs to be stratified by variances,  subgroup variances differ significantly, making each subgroup sampling size proportional to the overall subgroup population cannot be guaranteed.

如果可用的数据不能代表整个分组人口，则子组大小被认为具有同样的重要性。在一些应用中，子群大小是根据可用数据量来决定的，而不是按照子群大小来衡量样本大小，这会在因素的影响中引入偏倚。在某些情况下，数据需要由方差分层，分组方差差异显著，使得每个分组抽样大小与整个分组总体成比例不能得到保证。

Block randomization is commonly used in the experiment with a relatively big sampling size to avoid the imbalance allocation of samples with important characteristics. In certain fields with strict requests of randomization such as clinical trials, the allocation would be predictable when there is no blinding process for conductors and the block size is limited. The blocks permuted randomization in strata could possibly cause an imbalance of samples among strata as the number of strata increases and the sample size is limited, For instance, there is a possibility that no sample is found meeting the characteristic of certain strata.[13] 

Stratified sampling can not be applied if the population cannot be completely assigned into strata, which would result in sample sizes proportional to sample available instead of overall subgroup population.

如果总体不能完全分配到地层中，那么分层抽样就不能应用，这将导致样本大小与可用样本成比例，而不是整个子群总体。 


The process of assigning samples into subgroups could involve overlapping if subjects meet the inclusion standard of multiple strata, which could result in a misrepresentation of the population.

如果受试者符合多个阶层的包含标准，将样本分配到各个子群组的过程可能会涉及重叠，这可能会导致人口的不正当手法引诱。

应用 Application

混杂因素在临床试验中很重要

Stratified random sampling is useful and productive in situations requiring different weightings on specific strata. In this way, the researchers can manipulate the selection mechanisms from each strata to amplify or minimize the desired characteristics in the survey result.[14] 分层随机试验在需要对特定层进行不同权重的情况下非常有用且富有成效。 通过这种方式，研究人员可以操纵每个层次的选择机制，以放大或最小化调查结果中所需的特征。[15]


Stratified randomization is helpful when researchers intend to seek for associations between two or more strata, as simple random sampling causes a larger chance of unequal representation of target groups. It is also useful when the researchers wish to eliminate confounders in observational studies as stratified random sampling allows the adjustments of covariances and the p-values for more accurate results.[16]

当研究人员打算寻找两个或多个层次之间的关联时，分层随机化很有帮助，因为简单的随机抽样会导致更大的可能出现目标群体的不平等代表性。当研究人员希望消除观察性研究中的 混杂因素 Confounder 时，它也很有用，因为分层随机试验允许调整 协方差 Covariances 和 p 值 p-values 以获得更准确的结果。 [17]

There is also a higher level of statistical accuracy for stratified random sampling compared with simple random sampling, due to the high relevance of elements chosen to represent the population.[5] The differences within the strata is much less compared to the one between strata. Hence, as the between-sample differences are minimized, the standard deviation will be consequently tightened, resulting in higher degree of accuracy and small error in the final results. This effectively reduces the sample size needed and increases cost-effectiveness of sampling when research funding is tight.

与简单随机抽样相比，分层随机抽样的统计准确度也更高，因为选择代表总体的元素具有高度相关性。[5]与分层之间的差异相比，分层内的差异要小得多。因此，随着样本间差异的最小化， 标准差 Standard deviation 也会随之收紧，从而导致最终结果的准确性更高，误差更小。当研究资金紧张时，这有效地减少了所需的样本量并提高了抽样的 成本效益 Cost-effectiveness 。

In real life, stratified random sampling can be applied to results of election polling, investigations into income disparities among social groups, or measurements of education opportunities across nations.[1]

在现实生活中，分层随机试验可应用于选举投票结果、社会群体收入差距调查或各国教育机会的衡量。 [1]

临床试验中的分层随机试验 Stratified randomization in clinical trials

In clinical trials, patients are stratified according to their social and individual backgrounds, or any factor that are relevant to the study, to match each of these groups within the entire patient population. The aim of such is to create a balance of clinical/prognostic factor as the trials would not produce valid results if the study design is not balanced.[18] The step of stratified randomization is extremely important as an attempt to ensure that no bias, delibrate or accidental, affects the representative nature of the patient sample under study.[19] It increases the study power, especially in small clinical trials(n<400), as these known clinical traits stratified are thought to effect the outcomes of the interventions.[20] It helps prevent the occurrence of type I error, which is valued highly in clinical studies.[21] It also has an important effect on sample size for active control equivalence trials and in theory, facilitates subgroup analysis and interim analysis.[21]

在 临床试验 Clinical trials 中，根据患者的社会和个人背景或与研究相关的任何因素对患者进行分层，以匹配整个患者群体中的每个组。 这样做的目的是建立临床/预后因素（prognostic factor）的平衡，因为如果研究设计不平衡，试验将不会产生有效的结果。[22] 分层随机化的步骤非常重要，因为它试图确保没有偏见、有意或无意地影响所研究患者样本的代表性。 [23] 它增加了研究能力，尤其是在小型临床试验中（n<400），因为这些已知的临床特征分层被认为会影响干预的结果。[24]它有助于防止在临床研究中受到高度重视的 I 型错误 Type I error 的发生。 [21]它还对主动对照等效试验的样本量产生重要影响，并且在理论上有助于 亚组分析 Subgroup analysis 和 中期分析 Interim analysis 。 [21]

Advantage

The advantages of stratified randomization include:

  1. Stratified randomization can accurately reflect the outcomes of the general population since influential factors are applied to stratify the entire samples and balance the samples' vital characteristics among treatment groups. For instance, applying stratified randomization to make a sample of 100 from the population can guarantee the balance of males and females in each treatment group, while using simple randomization might result in only 20 males in one group and 80 males in another group.[8]
  2. Stratified randomization makes a smaller error than other sampling methods such as cluster sampling, simple random sampling, and systematic sampling or non-probability methods since measurements within strata could be made to have a lower standard deviation. Randomizing divided strata are more manageable and cheaper in some cases than simply randomizing general samples.[12]

优势 Advantage

分层随机试验的优点包括：

  1. 分层随机试验可以准确反映一般人群的结果，因为应用影响因素对整个样本进行分层并平衡样本在治疗组之间的重要特征。例如，采用分层随机化从人群中抽取 100 名样本可以保证每个治疗组的男女平衡，而使用简单随机化可能会导致一组只有 20 名男性，而另一组有 80 名男性。[8]
  2. 分层随机试验比其他抽样方法（例如 整群抽样 Cluster sampling 、简单随机抽样 和 系统抽样 Systematic sampling 或 非概率方法 Non-probability methods ）的误差更小，因为可以使分层内的测量具有较低的标准差。在某些情况下，将分割的分层随机试验比简单地随机试验一般样本更易于管理且成本更低。[12]
  3. 由于分层随机试验本质的精确性，团队更容易接受分层样本的训练。
  4. 由于这种方法的统计准确性，研究人员可以通过分析小样本得到非常有用的结果。
  5. 这种抽样技术涵盖了广泛的总体，因为已经对分层划分进行了完整的 charge。 This sampling technique covers a wide range of population since complete charge over the strata division has been made.
  1. 有时需要分层随机试验来估计总体中各组的总体参数。[12]

缺点 Disadvantage

The limits of stratified randomization include:

  1. Stratified randomization firstly divides samples into several strata with reference to prognostic factors but there is possible that the samples are unable to be divided. In application, the significance of prognostic factors lacks strict approval in some cases, which could further result in bias. This is why the factors' potential for making effects to result should be checked before the factors are included in stratification. In some cases that the impact of factors on the outcome cannot be approved, unstratified randomization is suggested.[25]
  2. The subgroup size is taken to be of the same importance if the data available cannot represent overall subgroup population. In some applications, subgroup size is decided with reference to the amount of data available instead of scaling sample sizes to subgroup size, which would introduce bias in the effects of factors.  In some cases that data needs to be stratified by variances, subgroup variances differ significantly, making each subgroup sampling size proportional to the overall subgroup population cannot be guaranteed.[26]
  3. Stratified sampling can not be applied if the population cannot be completely assigned into strata, which would result in sample sizes proportional to sample available instead of overall subgroup population.[8]
  4. The process of assigning samples into subgroups could involve overlapping if subjects meet the inclusion standard of multiple strata, which could result in a misrepresentation of the population.[26]

分层随机化的限制包括：

分层随机化首先参考预后因素将样本分成若干层，但有可能无法划分样本。在应用中，在某些情况下，预后因素的重要性缺乏严格的认可，这可能进一步导致偏差。这就是为什么在将因素纳入分层之前应该检查因素产生影响的潜力的原因。在某些因素对结果的影响无法得到批准的情况下，建议进行无分层随机化。 [18] 如果可用数据不能代表整个亚组人口，则认为亚组大小具有相同的重要性。在某些应用程序中，子组大小是根据可用数据量来决定的，而不是将样本大小缩放到子组大小，这会在因子效应中引入偏差。在某些需要对数据进行方差分层的情况下，子组方差差异显着，使得每个子组的抽样规模无法保证与整个子组总体成正比。 [19] 如果人口不能完全分配到层中，则不能应用分层抽样，这将导致样本大小与可用样本成正比，而不是与总体子组人口成正比。 [7] 如果受试者符合多层次的纳入标准，则将样本分配到亚组的过程可能涉及重叠，这可能导致总体的错误陈述。 [19]

  1. It is easier for a team to be trained to stratify a sample because of the exactness of the nature of stratified randomization.[8]
  2. Researchers can get highly useful results by analyzing smaller sample sizes because of statistical accuracy of this method.
  3. This sampling technique covers a wide range of population since complete charge over the strata division has been made.
  4. Sometimes stratified randomization is desirable to have estimates of population parameters for groups within the population.[12]
  1. ↑ 1.0 1.1 1.2 1.3 1.4 Nickolas, Steven (July 14, 2019). "How Stratified Random Sampling Works". Investopedia (in English). Retrieved 2020-04-07.
  2. ↑ "Simple random sample", Wikipedia (in English), 2020-03-18, retrieved 2020-04-07
  3. ↑ "Stratified sampling", Wikipedia (in English), 2020-02-09, retrieved 2020-04-07
  4. ↑ 4.0 4.1 Stephanie (Dec 11, 2013). "Stratified Random Sample: Definition, Examples". Statistics How To (in English). Retrieved 2020-04-07.
  5. ↑ 5.0 5.1 5.2 5.3 5.4 "Stratified Random Sampling: Definition, Method and Examples". QuestionPro (in English). 2018-03-13. Retrieved 2020-04-07.
  6. ↑ Sylvester, Richard (December 1982). "Fundamentals of clinical trials". Controlled Clinical Trials. 3 (4): 385–386. doi:10.1016/0197-2456(82)90029-0. ISSN 0197-2456.
  7. ↑ Sylvester, Richard (December 1982). "Fundamentals of clinical trials". Controlled Clinical Trials. 3 (4): 385–386. doi:10.1016/0197-2456(82)90029-0. ISSN 0197-2456.
  8. ↑ 8.0 8.1 8.2 8.3 8.4 8.5 8.6 8.7 8.8 8.9 Pocock, Stuart J. (Jul 1, 2013). Clinical trials : a practical approach. Chichester: John Wiley & Sons Ltd. ISBN 978-1-118-79391-6. OCLC 894581169. 
  9. ↑ "Sealed Envelope | Random permuted blocks". www.sealedenvelope.com. Feb 25, 2020. Retrieved 2020-04-07.
  10. ↑ Friedman, Lawrence M.; Furberg, Curt D.; DeMets, David L. (2010), "Introduction to Clinical Trials", Fundamentals of Clinical Trials, Springer New York, pp. 1–18, doi:10.1007/978-1-4419-1586-3_1, ISBN 978-1-4419-1585-6
  11. ↑ Fundamentals of clinical trials. Friedman, Lawrence M., 1942-, Furberg, Curt,, DeMets, David L., 1944-, Reboussin, David,, Granger, Christopher B. (Fifth ed.). New York. 27 August 2015. ISBN 978-3-319-18539-2. OCLC 919463985. 
  12. ↑ 12.0 12.1 12.2 12.3 12.4 12.5 Pocock, S. J. (March 1979). "Allocation of Patients to Treatment in Clinical Trials". Biometrics. 35 (1): 183–197. doi:10.2307/2529944. ISSN 0006-341X. JSTOR 2529944. PMID 497334.
  13. ↑ Fundamentals of clinical trials. Friedman, Lawrence M., 1942-, Furberg, Curt,, DeMets, David L., 1944-, Reboussin, David,, Granger, Christopher B. (Fifth ed.). New York. 27 August 2015. ISBN 978-3-319-18539-2. OCLC 919463985. 
  14. ↑ Crossman, Ashley (Jan 27, 2020). "Understanding Stratified Samples and How to Make Them". ThoughtCo (in English). Retrieved 2020-04-07.
  15. ↑ Crossman, Ashley (Jan 27, 2020). "Understanding Stratified Samples and How to Make Them". ThoughtCo (in English). Retrieved 2020-04-07.
  16. ↑ Hennekens, Charles H. (1987). Epidemiology in medicine. Buring, Julie E., Mayrent, Sherry L. (1st ed.). Boston, Massachusetts: Little, Brown. ISBN 0-316-35636-0. OCLC 16890223. 
  17. ↑ Hennekens, Charles H. (1987). Epidemiology in medicine. Buring, Julie E., Mayrent, Sherry L. (1st ed.). Boston, Massachusetts: Little, Brown. ISBN 0-316-35636-0. OCLC 16890223. 
  18. ↑ Polit, DF; Beck, CT (2012). Nursing Research: Generating and Assessing Evidence for Nursing Practice, 9th ed.. Philadelphia, USA: Wolters Klower Health: Lippincott Williams & Wilkins.. 
  19. ↑ "Patient Stratification in Clinical Trials". Omixon | NGS for HLA (in English). 2014-12-01. Retrieved 2020-04-26.
  20. ↑ Stephanie (2016-05-20). "Stratified Randomization in Clinical Trials". Statistics How To (in English). Retrieved 2020-04-26.
  21. ↑ 21.0 21.1 21.2 21.3 Kernan, W (Jan 1999). "Stratified Randomization for Clinical Trials". Journal of Clinical Epidemiology. 52 (1): 19–26. doi:10.1016/S0895-4356(98)00138-3. PMID 9973070.
  22. ↑ Polit, DF; Beck, CT (2012). Nursing Research: Generating and Assessing Evidence for Nursing Practice, 9th ed.. Philadelphia, USA: Wolters Klower Health: Lippincott Williams & Wilkins.. 
  23. ↑ "Patient Stratification in Clinical Trials". Omixon | NGS for HLA (in English). 2014-12-01. Retrieved 2020-04-26.
  24. ↑ Stephanie (2016-05-20). "Stratified Randomization in Clinical Trials". Statistics How To (in English). Retrieved 2020-04-26.
  25. ↑ Murphy, Chris B. (Apr 13, 2019). "Pros and Cons of Stratified Random Sampling". Investopedia (in English). Retrieved 2020-04-07.
  26. ↑ 26.0 26.1 Glass, Aenne; Kundt, Guenther (2014), "Potential Advantages and Disadvantages of Stratification in Methods of Randomization", Springer Proceedings in Mathematics & Statistics, Springer New York, pp. 239–246, doi:10.1007/978-1-4939-2104-1_23, ISBN 978-1-4939-2103-4
取自“https://wiki.swarma.org/index.php?title=分层随机试验&oldid=23504”