蚁群算法

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
费米子（讨论 | 贡献）2020年4月9日 (四) 14:28的版本 （→‎基本流程）
跳到导航 跳到搜索

蚁群算法 Ant Colony Optimization（ACO）是一种用来寻找优化路径的概率型算法。它由Marco Dorigo于1992年在他的博士论文中提出，其灵感来源于蚂蚁在寻找食物过程中发现路径的行为。

蚂蚁集体寻食行为
当蚂蚁在通往食物的路上面临选择（有一条路会比另外的更短），他们的选择完全是随机的。但是那些通过更短的路更快找到食物的蚂蚁，他们会更多地选择从这条路通过

人工蚂蚁代表受实际蚂蚁行为启发的多智能体方法。 基于信息素的蚂蚁交流通常是主要被考虑的蚂蚁行为。[1]人工蚂蚁和局部搜索算法的结合已成为众多优化任务的一种选择方法，这些优化任务涉及某种图形，例如车辆路线 Vehicle routing 和互联网路线 Iinternet routing。 该领域蓬勃发展，专门针对人工蚁群算法的会议以及由诸如AntOptima之类的专门公司进行的大量商业应用都应用而生。

在群体智能方法中，该算法是蚁群算法家族的成员，它构成了一些元启发式优化。 Marco Dorigo最初于1992年在其博士学位论文中提出[2]，这种算法旨在根据蚂蚁在蚁穴和食物来源之间寻找路径的行为来在图中寻找最佳路径。

这种算法具有分布计算、信息正反馈和启发式搜索的特征，本质上是进化算法中的一种启发式全局优化算法。

背景

算法起源

  • 蚁群系统 Ant System 是由意大利学者Dorigo、Maniezzo等人于1991年首先提出来的，用于解决TSP问题。他们在研究蚂蚁觅食的过程中，发现单个蚂蚁的行为比较简单，但是蚁群整体却可以体现一些智能的行为。例如蚁群可以在不同的环境下，寻找最短到达食物源的路径。

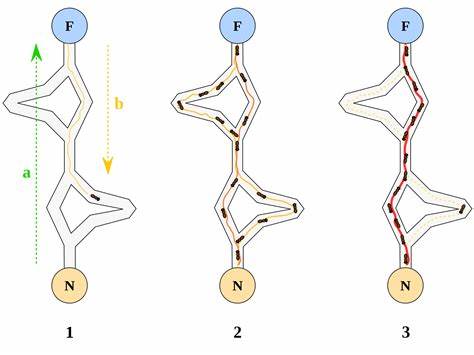
这是因为蚁群内的蚂蚁可以通过某种信息机制实现信息的传递。后又经进一步研究发现，蚂蚁会在其经过的路径上释放一种可以称之为 “信息素 pheromone” 的物质，蚁群内的蚂蚁对“信息素”具有感知能力，它们会沿着“信息素”浓度较高路径行走，而每只路过的蚂蚁都会在路上留下“信息素”，这就形成一种类似正反馈的机制，这样经过一段时间后，整个蚁群就会沿着最短路径到达食物源了。

  • 1995年Gramdardella和Dorigo提出Ant-Q算法，建立了AS和Q-learning的联系；
  • 1996年又提出Ant Colony System；
  • 1997年又提出Max-Min Ant System；
  • 1996年Dorigo等人把先前各种算法归结为Ant Colony Optimization meta-heuristic的统一框架下，给出抽象而规范的算法描述；

算法原理

  • 蚂蚁在运动过程中，能够在它所经过的路径上留下外激素，并且可以再运动过程中感知外激素的存在和强度，并且以此指导自己的运动方向——外激素强度越高蚂蚁选择走该路径的概率就越大；
  • 由大量蚂蚁组成的一群的集体行为便表现出一种信息正反馈现象：从某一路径上走过的蚂蚁越多，那么后来者选择该路径的概率就越大。蚂蚁个体之间就是通过这种信息的交流达到搜索食物的目的。

简化版蚂蚁寻食过程

假设蚂蚁每经过一处所留下的信息素为一个单位，则经过36个时间单位后，所有开始一起出发的蚂蚁都经过不同路径从D点取得了食物，此时，ABD路线往返了2趟，每一处的信息素为4个单位，而ACD的路线上往返了一趟，每一处的信息素为2个单位，其比值为2 : 1。

然后，蚂蚁继续寻找食物，按照信息素指导，蚂蚁在ABD路线上增派一只蚂蚁（共2只），而ACD路线上仍然有一只蚂蚁。再经过36个时间单位后，两条线路上的信息素单位积累为12和4，比值为3 : 1。

若按以上规则继续，蚁群在ABD路线上再增派一只蚂蚁（共3只），而ACD路线上仍然为一只蚂蚁，再经过36个时间单位后，两条线路上的信息素单位积累为24和6，比值为4 : 1。

继续进行，按照信息素指导，最终所有的蚂蚁都会放弃ACD路线，而都选择ABD路线，即正反馈效应。

人工蚁群算法

基于以上一群寻找食物时的最优路径选择问题，可以构造人工蚁群，来解决最优化问题（如TSP问题）。

蚁群觅食 蚁群优化算法
蚁群 搜索空间的一组有效解（表现为种群规模N）
信息素 信息素浓度变量
蚁巢到食物的一条路径 一个有效解
找到的最短路径 问题的最优解

算法内容

基本思想

  1. 根据具体问题设置多只蚂蚁，分头并行搜索。
  2. 每只蚂蚁完成一次周游后，在行进的路上释放信息素，信息素量与解的质量成正比。
  3. 蚂蚁路径的选择根据信息素强度大小（初始信息素量设为相等），同时考虑两点之间的距离，采用随机的局部搜索策略。这使得距离较短的边，其上的信息素量较大，后来的蚂蚁选择该边的概率也较大。
  4. 每只蚂蚁只能走合法路线（经过每个城市1次且仅1次），为此设置禁忌表来控制。
  5. 所有蚂蚁都搜索完一次就是迭代一次，每迭代一次就对所有的边做一次信息素更新，原来的蚂蚁死掉，新的蚂蚁进行新一轮搜索。
  6. 更新信息素包括原有信息素的蒸发和经过的路径上信息素的增加。
  7. 达到预定的迭代步数，或出现停滞现象（所有蚂蚁都选择同样的路径，解不再变化），则算法结束，以当前最优解作为问题的最优解。

总结后的要点即为 1. 状态转移 2. 信息素更新

基本蚁群算法原理推导

定义算法的关键参数如下：

[math]\displaystyle{ {m} }[/math] ：蚂蚁数量
[math]\displaystyle{ {M} }[/math] ：城市数量
[math]\displaystyle{ {\rho} }[/math] ：信息素挥发因子，表示信息素的持久度，推荐值为[0,1]
[math]\displaystyle{ {Q} }[/math] ：常量，表示信息素浓度
[math]\displaystyle{ {L_k} }[/math] ：表示第k只蚂蚁在本次迭代中路程的代价
[math]\displaystyle{ {\alpha} }[/math] ：信息素启发因子，表示在搜索中，信息量的相对重要程度
[math]\displaystyle{ {\beta} }[/math] ：期望启发因子，表示在搜索中，启发式信息的相对重要程度

一般：

[math]\displaystyle{ {m=1.5\times M} }[/math]
[math]\displaystyle{ {\rho \in [0.2,0.5] } }[/math]
[math]\displaystyle{ {Q \in [10,100] } }[/math]
[math]\displaystyle{ {\alpha \in [0,5] } }[/math]
[math]\displaystyle{ {\beta \in [0,5] } }[/math]

设第[math]\displaystyle{ {k} }[/math]只蚂蚁现在城市[math]\displaystyle{ {i} }[/math]，城市[math]\displaystyle{ {i} }[/math] 到[math]\displaystyle{ {j} }[/math]，[math]\displaystyle{ {j \in [1, M] } }[/math] 的距离为[math]\displaystyle{ {d_{ij}} }[/math]，从城市[math]\displaystyle{ {i} }[/math] 到[math]\displaystyle{ {j} }[/math]的信息素浓度为[math]\displaystyle{ {\rho_{ij}} }[/math]。当蚂蚁[math]\displaystyle{ {k} }[/math]选择下一个将要前往的城市时，则根据各城市距离和信息素计算前往该城市的概率为：

[math]\displaystyle{ {q_{ij}=p_{ij}^{\alpha}\times ({\frac{1}{d_{i,j}})}^{\beta}} }[/math]

当蚂蚁k走完所有的城市，就得出了一条对应的搜索路径，先更新信息素浓度：

[math]\displaystyle{ {p_{ij}=\rho*p_{i,j}+\frac{Q}{sum}} }[/math]

其中sum为每一个蚂蚁走过的距离之和。 然后将该搜索路径和其他蚂蚁对比，选择长度最短的那个蚂蚁，作为“最优蚂蚁”路径查找结果，本轮迭代结束，进入下一轮。

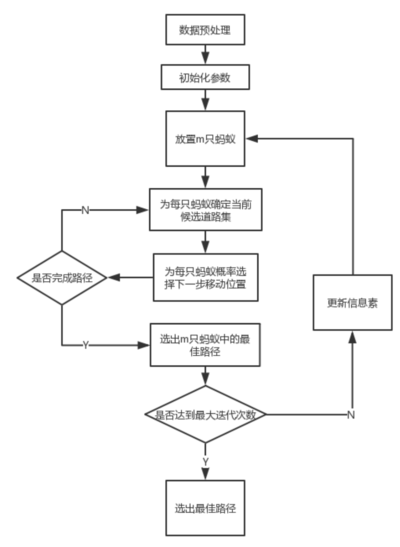
算法流程图

下面给出蚁群算法的算法流程图：

ACO蚁群算法流程图“CSDN——ACO 蚁群算法”，其中初始化和其他群算法一致，唯一区别在于，蚁群算法的位置更新根据上述计算的概率进行选择。

算法应用——以TSP问题为例

蚁群算法具有鲁棒性强、全局搜索、并行分布式计算、易于其他问题结合等优点。近年来，蚁群算法应用领域不断扩张——从旅行商问题 Traveling Salesman Problem、指派问题、图着色问题 Graph Coloring Problem、网络路由问题 Network Routing Problem 到车间调度问题、车辆路径问题 Vehicle Routing Problem、分配问题等等，这些问题总结起来主要是NP难的组合优化问题，用传统算法难以求解或者无法求解。

下面以最经典的TSP问题为例，使用蚁群算法进行求解[1]。

问题说明

旅行商问题，即TSP问题 Traveling Salesman Problem 又译为旅行推销员问题、货郎担问题，是数学领域中著名问题之一。 问题：假设有一个旅行商人要拜访N个城市（表示为有向图[math]\displaystyle{ {G = (N, A)} }[/math]，其中[math]\displaystyle{ {N = {1,2,\cdots,n}} }[/math]，[math]\displaystyle{ {A=\left \{ \right.(i,j)| i,j \in N\left. \right \}} }[/math]，城市之间距离 ），他必须选择所要走的路径，路径的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。 目标函数为：

[math]\displaystyle{ {f(w)=\sum_{l=1}^{n} d_{i_{l-1} i_l'}} }[/math]

其中[math]\displaystyle{ {w=(i_1,i_2,\cdots, i_n)} }[/math] 为城市[math]\displaystyle{ {1,2,\cdots,n} }[/math]的一个排列，[math]\displaystyle{ {i_{n+1}=i_l} }[/math]。

蚁群算法思路

  • TSP问题的人工蚁群算法中，假设m只蚂蚁在图的相邻节点间移动，从而通过协作得到问题的解。每只蚂蚁的一步转移概率由图中的每条边上的两类参数决定：信息素值和可见度（即先验值）；
  • 信息素的更新方式有两种：一是挥发，也就是所有路径上的信息素以一定的比率减少，模拟自然蚁群的信息素随时间挥发的过程；二是增强，给评价值为正反馈（有蚂蚁走过）的边增加信息素；
  • 蚂蚁向下一个目标的运动是通过一个随机原则来实现的，也就是运用当前所有节点存储的信息，计算出下一步可到达节点的概率，并按照此概率实现一步移动，按此循环，越来越接近最优解；
  • 蚂蚁在寻找过程中，或者找到一个解后，会评估该解或解的一部分的优化程度，并把评价信息保存在相关连接的信息素中。

基本流程

主要分为两步：路径构建和信息素更新[3]。

（1）路径构建

每个蚂蚁都随机选择一个城市作为其出发城市，并维护一个路径记忆向量，用来存放该蚂蚁依次经过的城市。蚂蚁在构建路径的每一步中，按照一个随机比例规则选择下一个要到达的城市。随机比例规则：

[math]\displaystyle{ {P_{ij}^k(t)=\begin{cases} \frac{{ \left [ \tau_{ij}(t) \right ]}^{\alpha}\times {\left [ \eta_{ij}(t) \right ]}^{\beta}}{\sum_{k\in allowed_k}{ \left [ \tau_{ij}(t) \right ]}^{\alpha}\times {\left [ \eta_{ij}(t) \right ]}^{\beta}} , & \text{if} \quad j \in allowed_k\\ 0 , & \text{others} \end{cases}} }[/math]

其中：

  • [math]\displaystyle{ {i,j} }[/math]分别为起点和终点；
  • [math]\displaystyle{ {\eta_{i,j}=\frac{1}{d_{ij}}} }[/math]为能见度，是两点路i，j距离的倒数；
  • [math]\displaystyle{ {\tau_{i,j}(t)} }[/math] 为时间t时由 i 到 j 的信息素浓度；
  • [math]\displaystyle{ {allowed_k} }[/math] 为尚未访问过的节点集合；
  • [math]\displaystyle{ {\alpha} }[/math]和 [math]\displaystyle{ {\beta} }[/math] 为两常数，分别是信息素和能见度的加权值。

（2）信息素更新

  • 初始化信息素浓度：[math]\displaystyle{ {\tau_{ij}(t)=C} }[/math]

注：如果[math]\displaystyle{ {C} }[/math]太小，算法容易早熟，蚂蚁会很快的全部集中到一条局部最优的路径上；相反，如果[math]\displaystyle{ {C} }[/math]太大，信息素对搜索方向的知道作用太低，也会影响算法性能。所以一般，[math]\displaystyle{ {C} }[/math]的取值为：

[math]\displaystyle{ {C=\frac{m}{C^{mn}}} }[/math]

  • 浓度更新：为了模拟蚂蚁在较短路径上留下更多的信息素，当所有蚂蚁到达重点时，必须把各路径的信息素浓度重新更新一次，信息素的更新也分两个步骤：首先，每一轮过后，问题空间中的所有路径上的信息素都会发生蒸发；然后，所有的蚂蚁根据自己构建的路径长度在它们本轮经过的边上释放信息素。更新过程如下：

[math]\displaystyle{ {t_{ij}(t)=(1-\rho) \tau_{ij}+\sum_{k=1}^m \Delta \tau _{ij}^k } }[/math]

其中[math]\displaystyle{ {m} }[/math]为蚂蚁个数，[math]\displaystyle{ 0\lt \rho \leq 1 }[/math]为信息素的蒸发率（通常为0.5），为第[math]\displaystyle{ {k} }[/math]只蚂蚁在路径 [math]\displaystyle{ {i} }[/math] 到 [math]\displaystyle{ {j} }[/math] 所留下来的信息素，其中：

[math]\displaystyle{ {\Delta \tau _{ij}^k=\begin{cases} {(C_k)}^{-1} ,& \text{ if the } k^{th} \text{ant travers} (i,j) \\ 0 ,& \text{others} \end{cases}} }[/math]

[math]\displaystyle{ {C_k} }[/math]是第[math]\displaystyle{ {k} }[/math]只蚂蚁走完整条路径后所得到的总路径长度。

伪代码

--------------*Pseudocode code of ACO for TSP *-------------------------
   Procedre AS
      for each edge 
         set initial pheromone value t0
      end for 
      while not stop 
         for each ant k
            randomly choose an initial city
            for I=1 to n
              choose next city j with probability 
            end for 
         end for 
         compute the length Ck of the tour constructed by the nth ant 
         for each edge 
             update the pheromone value 
         end for 
      end while 
      print results 
   end procedure

举例

（1）问题——四个城市之间的TSP问题： 距离矩阵和城市图示如下：

Matrix.png

（2）求解

设共有[math]\displaystyle{ {m=3} }[/math]只蚂蚁，参数[math]\displaystyle{ {\alpha=1, \beta=2,\rho=0.5} }[/math]

步骤1：初始化

先使用贪心法得到路径（ACDBA），则有：

[math]\displaystyle{ {C_{nm}=1+2+4+3=10} }[/math]

求得：

[math]\displaystyle{ {\tau_0=\frac{m}{C_{mn}}=0.3} }[/math]

[math]\displaystyle{ {\tau(0)=(\tau_{ij}(0))=\begin{pmatrix} 0 & 0.3 & 0.3 & 0.3 \\ 0.3 & 0 & 0.3 & 0.3 \\ 0.3 & 0.3 & 0 & 0.3\\ 0.3 & 0.3 & 0.3 & 0 \end{pmatrix}} }[/math]

步骤2：随机选择每个蚂蚁的出发城市

设蚂蚁1选择城市A，蚂蚁2选择城市B，蚂蚁3选择城市D。

步骤3.1：选择每个蚂蚁的下一访问城市

以蚂蚁1为例，当前城市[math]\displaystyle{ {i=A} }[/math]，可访问城市集合，计算蚂蚁1访问各个城市的概率：

[math]\displaystyle{ {A=\begin{cases} B: \tau_{AB}^{\alpha} \times \eta_{AB}^{\beta}=0.3^1+(1/3)^2=0.033 \\ C: \tau_{AC}^{\alpha} \times \eta_{AC}^{\beta}=0.3^1+(1/1)^2=0.300 \\ D: \tau_{AD}^{\alpha} \times \eta_{AD}^{\beta}=0.3^1+(1/3)^2=0.075 \end{cases}} }[/math]

[math]\displaystyle{ { \begin{array}{lcl} p(B) = 0.033/(0.033+0.3+0.075) = 0.018 \\ p(C) = 0.3/(0.033+0.3+0.075) = 0.74 \\ p(D) = 0.075/(0.033+0.3+0.075) = 0.18 \\ \end{array} } }[/math]

用轮盘赌法选择下一个访问城市。假设产生的随机数[math]\displaystyle{ {q=0.05} }[/math]，则蚂蚁1会选择城市B。同样，假设蚂蚁2选择城市D，蚂蚁3选择城市A。

步骤3.2：再选择每个蚂蚁的下一访问城市

同样，以蚂蚁1为例，当前城市[math]\displaystyle{ {i=B} }[/math]，路径记忆向量 [math]\displaystyle{ {R^t=(AB)} }[/math] ，可访问城市集合[math]\displaystyle{ {J_1(i)=\left [ C, D\right ]} }[/math] ，计算蚂蚁1访问C,D城市的概率：

[math]\displaystyle{ {B\Rightarrow \begin{cases} C: \tau_{BC}^{\alpha}\times \eta_{BC}^{\beta}=0.3^1+{(1/5)}^2=0.012\\ D: \tau_{BD}^{\alpha}\times \eta_{BD}^{\beta}=0.3^1+{(1/4)}^2=0.019 \end{cases}} }[/math]

[math]\displaystyle{ { \begin{array}{lcl} p(C) = 0.012/(0.012+0.019) = 0.39 \\ p(D) = 0.019/(0.012+0.019) = 0.61 \\ \end{array} } }[/math]

用轮盘赌法选择下一个访问城市。假设产生的随机数q = 0.67，则蚂蚁1会选择城市D。同样，假设蚂蚁2选择城市C，蚂蚁3选择城市D。 至此，所有蚂蚁的路径均构造完毕——蚂蚁1：ABDCA，蚂蚁2：BDCAB，蚂蚁3：DACBD

步骤4：信息素更新

计算每只蚂蚁构建的路径长度：

[math]\displaystyle{ { \begin{array}{lcl} C1 = 3 + 4 + 2 + 1 = 10 \\ C2 = 4 + 2 + 1 + 3 = 10 \\ C3 = 2 + 1 + 5 + 4 = 12 \\ \end{array} } }[/math]


更新每条边上的信息素：

[math]\displaystyle{ { \begin{array} {lccl} \tau_{AB}=(1-\rho)\times \tau_{AB}+\sum_{k=1}^3\Delta \tau_{AB}^k=0.5\times 0.3 +(1/10+1/10)=0.35 \\ \tau_{AC}=(1-\rho)\times \tau_{AC}+\sum_{k=1}^3\Delta \tau_{AC}^k=0.5\times 0.3 +(1/12)=0.16\\ \cdots \end{array} } }[/math]

步骤5：如果满足条件，则输出全局最优结果并结束程序，否则转向步骤2继续执行。

解决TSP问题的Python 代码实现

先创建一个文件命名为MyFuncTool.py，在这里定义函数 GetData，主要用来提取数据：城市位置和城市间距离。定义函数ResultShow用来输出最后结果。函数draw用于最后画结果图[2]。 

# -*- coding: utf-8 -*-
"""
	基于贪心算法的旅行商问题解法Python源码
	
	Author:	Greatpan
	Date:	2018.9.30
"""
import pandas
import numpy as np
import math
import matplotlib.pyplot as plt 

class Node:
	"""
		类名：Node
		类说明：	城市节点类
	"""
	def __init__(self,CityNum):
		"""
		函数名：GetData()
		函数功能：	从外界读取城市数据并处理
			输入	无
			输出	1 Position：各个城市的位置矩阵
				2 CityNum：城市数量
				3 Dist：城市间距离矩阵
		其他说明：无
		"""
		self.visited=[False]*CityNum    #记录城市是否走过
		self.start=0                    #起点城市
		self.end=0                      #目标城市
		self.current=0                  #当前所处城市
		self.num=0                      #走过的城市数量
		self.pathsum=0                  #走过的总路程
		self.lb=0                       #当前结点的下界
		self.listc=[]                   #记录依次走过的城市

def GetData(datapath):
	"""
	函数名：GetData()
	函数功能：	从外界读取城市数据并处理
		输入	无
		输出	1 Position：各个城市的位置矩阵
			2 CityNum：城市数量
			3 Dist：城市间距离矩阵
	其他说明：无
	"""
	dataframe = pandas.read_csv(datapath,sep=" ",header=None)
	Cities = dataframe.iloc[:,1:3]
	Position= np.array(Cities)				#从城市A到B的距离矩阵
	CityNum=Position.shape[0]				#CityNum:代表城市数量
	Dist = np.zeros((CityNum,CityNum))		#Dist(i,j)：城市i与城市j间的距离

	#计算距离矩阵
	for i in range(CityNum):
		for j in range(CityNum):
			if i==j:
				Dist[i,j] = math.inf
			else:
				Dist[i,j] = math.sqrt(np.sum((Position[i,:]-Position[j,:])**2))
	return Position,CityNum,Dist

def ResultShow(Min_Path,BestPath,CityNum,string):
	"""
		函数名：GetData()
		函数功能：	从外界读取城市数据并处理
			输入	无
			输出	1 Position：各个城市的位置矩阵
				2 CityNum：城市数量
				3 Dist：城市间距离矩阵
		其他说明：无
	"""
	print("基于"+string+"求得的旅行商最短路径为：")
	for m in range(CityNum):
		print(str(BestPath[m])+"—>",end="")
	print(BestPath[CityNum])
	print("总路径长为："+str(Min_Path))
	print()

def draw(BestPath,Position,title):
	"""
		函数名：draw(BestPath,Position,title)
		函数功能：	通过最优路径将旅行商依次经过的城市在图表上绘制出来
			输入	1 	BestPath：最优路径
				2	Position：各个城市的位置矩阵
				3	title:图表的标题
			输出	无
		其他说明：无
	"""
	plt.title(title) 
	plt.plot(Position[:,0],Position[:,1],'bo')
	for i,city in enumerate(Position): 
		plt.text(city[0], city[1], str(i)) 
	plt.plot(Position[BestPath, 0], Position[BestPath, 1], color='red') 
	plt.show()

这里开始代码的主要部分： 

# -*- coding: utf-8 -*-
"""
	基于回溯法的旅行商问题解法Python源码
	
	Author:		Greatpan
	Date:		2018.10.10
"""

from MyFuncTool import GetData,ResultShow,draw
import time
import numpy as np

def ant():
	"""
		函数名：ant()
		函数功能：蚁群算法核心
		输入    1: 无
		输出    1: 无
		其他说明：无
	"""
	numant = 25          # 蚂蚁个数
	numcity = CityNum   # 城市个数
	alpha = 1           # 信息素重要程度因子
	rho = 0.1           # 信息素的挥发速度
	Q = 1
	
	iters = 0
	itermax = 500
	
	etatable = 1.0/(Dist+np.diag([1e10]*numcity))       # 启发函数矩阵，表示蚂蚁从城市i转移到矩阵j的期望程度
	pheromonetable  = np.ones((numcity,numcity))        # 信息素矩阵
	pathtable = np.zeros((numant,numcity)).astype(int)  # 路径记录表
	
	lengthaver = np.zeros(itermax)          # 各代路径的平均长度
	lengthbest = np.zeros(itermax)          # 各代及其之前遇到的最佳路径长度
	pathbest = np.zeros((itermax,numcity))  # 各代及其之前遇到的最佳路径

	while iters < itermax:
		#  随机产生各个蚂蚁的起点城市
		if numant <= numcity:   # 城市数比蚂蚁数多
			pathtable[:,0] = np.random.permutation(range(0,numcity))[:numant]
		else:                   # 蚂蚁数比城市数多，需要补足
			pathtable[:numcity,0] = np.random.permutation(range(0,numcity))[:]
			pathtable[numcity:,0] = np.random.permutation(range(0,numcity))[:numant-numcity]
		
		length = np.zeros(numant)       # 计算各个蚂蚁的路径距离
		
		for i in range(numant):
			visiting = pathtable[i,0]   # 当前所在的城市
			
			# visited = set()                 # 已访问过的城市，防止重复
			# visited.add(visiting)           # 增加元素
			unvisited = set(range(numcity))   # 未访问的城市
			unvisited.remove(visiting)        # 删除元素
			
			for j in range(1,numcity):        # 循环numcity-1次，访问剩余的numcity-1个城市
				# 每次用轮盘法选择下一个要访问的城市
				listunvisited = list(unvisited)
				probtrans = np.zeros(len(listunvisited))
				
				for k in range(len(listunvisited)):
					probtrans[k] = np.power(pheromonetable[visiting][listunvisited[k]],alpha)\
						*np.power(etatable[visiting][listunvisited[k]],alpha)
				cumsumprobtrans = (probtrans/sum(probtrans)).cumsum()
				cumsumprobtrans -= np.random.rand()
				
				k = listunvisited[np.where(cumsumprobtrans>0)[0][0]] # 下一个要访问的城市
				pathtable[i,j] = k
				unvisited.remove(k)
				#visited.add(k)
				length[i] += Dist[visiting][k]
				visiting = k
			
			length[i] += Dist[visiting][pathtable[i,0]] # 蚂蚁的路径距离包括最后一个城市和第一个城市的距离
		
		
		# 包含所有蚂蚁的一个迭代结束后，统计本次迭代的若干统计参数
		lengthaver[iters] = length.mean()
		if iters == 0:
			lengthbest[iters] = length.min()
			pathbest[iters] = pathtable[length.argmin()].copy()      
		else:
			if length.min() > lengthbest[iters-1]:
				lengthbest[iters] = lengthbest[iters-1]
				pathbest[iters] = pathbest[iters-1].copy()
			else:
				lengthbest[iters] = length.min()
				pathbest[iters] = pathtable[length.argmin()].copy()    
		
		# 更新信息素
		changepheromonetable = np.zeros((numcity,numcity))
		for i in range(numant):
			for j in range(numcity-1):
				changepheromonetable[pathtable[i,j]][pathtable[i,j+1]] += Q/length[i]
			changepheromonetable[pathtable[i,j+1]][pathtable[i,0]] += Q/length[i]
		pheromonetable = (1-rho)*pheromonetable + changepheromonetable
		
		# 迭代次数指示器+1
		iters += 1 

	path_tmp=pathbest[-1]
	BestPath=[]
	for i in path_tmp:
		BestPath.append(int(i))
	BestPath.append(BestPath[0])
	
	return BestPath,lengthbest[-1]

##############################程序入口#########################################
if __name__ == "__main__":
	Position,CityNum,Dist = GetData("./data/TSP25cities.tsp") #此处可以更改为你的数据所在的路径和文件名
	
	start = time.clock()                # 程序计时开始
	BestPath,Min_Path = ant()
	end = time.clock()                  # 程序计时结束
	
	print()
	ResultShow(Min_Path,BestPath,CityNum,"蚁群算法")
	draw(BestPath,Position,"Ant Method")

在这个问题中，我们把城市的数据存在csv文档中，并把文档命名为TSP25cities.tsp。 

1 2374 197
2 2166 878
3 644 5
4 268 3149
5 706 2256
6 2180 2557
7 1397 771
8 1356 42
9 430 1110
10 2827 1530
11 762 2418
12 1150 1031
13 2227 1932
14 690 2003
15 514 1034
16 310 397
17 1506 2494
18 506 1023
19 2832 366
20 12 2743
21 408 1154
22 2189 3038
23 220 703
24 849 2570
25 2424 392

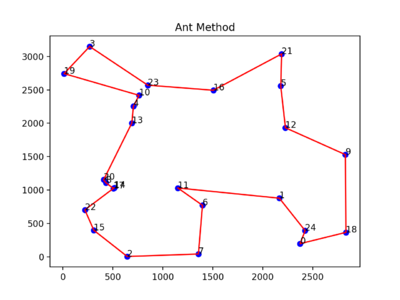
基于上述代码的实现结果如下所示： 基于蚁群算法求得的旅行商最短路径为： 

3—>19—>10—>4—>13—>20—>8—>17—>14—>22—>15—>2—>7—>6—>11—>1—>24—>0—>18—>9—>12—>5—>21—>16—>23—>3
总路径长为：13489.663390290067

其结果图如下：

根据蚁群算法得出的TSP问题路线图

常见算法变形

这里展示了一些常见的蚁群算法的变形算法。

蚂蚁系统 Ant System (AS)

蚂蚁系统是第一个蚁群算法家族的算法，这个算法就是以上介绍的算法思想，由Dorigo提出。

蚁群系统 Ant Colony System (ACS)

在蚁群系统算法中，原始的蚁群系统在三个方面进行了修改[4]：

（i）边缘选择偏向开发（即倾向于选择具有大量信息素的最短边缘的可能性）;

（ii）在构建解决方案时，蚂蚁通过应用局部信息素更新规则来更改其选择的边缘的信息素级别；

（iii）在每次迭代结束时，仅允许最佳蚂蚁通过应用修改后的全局信息素更新规则来更新路径。

精英蚂蚁系统 Elitist Ant System

在这个算法里，全局最优解和其他的蚂蚁一样在每一次迭代后在他的路径上留下信息素（即使这条路径没有被再次访问）。

Max-Min 蚂蚁系统 Max-Min Ant System(MMAS)

该算法控制每个路径上的最大和最小信息素量。 仅允许全局最佳巡回或迭代最佳巡回将信息素添加到其踪迹中。 为了避免搜索算法的停滞，将每条路径上可能的信息素数量的范围限制为间隔[math]\displaystyle{ {\left [ \tau_{max},\tau_{min} \right ]} }[/math]。 将所有边都初始化为[math]\displaystyle{ \tau_{max} }[/math]以强制对解进行更高的探索。 临近停滞时，这些路径会重新初始化为[math]\displaystyle{ \tau_{max} }[/math]。[5]

基于排序的蚁群系统 Rank-based Ant System(ASrank)

所有解决方案均根据其长度进行排名。 此迭代中只允许固定数量的最佳蚂蚁更新其路径。 对解根据其信息素量加权，以使路径较短的解比路径较长的解具有更多的信息素[6]。

连续正交的蚂蚁系统 Continuous Orthogonal Ant Colony(COAC)

COAC的信息素沉积机制是为了使蚂蚁能够协同有效地寻找解决方案。 通过使用正交设计方法，可行域中的蚂蚁可以快速有效地探索其选择的区域，并能够增强全局搜索能力和搜索准确性。 正交设计方法和自适应半径调整方法也可以扩展到其他优化算法，从而在解决实际问题上具有更广泛的优势[7]。

递归蚁群优化 Recursive Ant Colony Optimization

它是蚂蚁系统的一种递归形式，它将整个搜索域划分为几个子域，并解决了这些子域的目标。[8]比较所有子域的结果，并将其中最好的几个提升到下一个级别。 进一步细分对应于所选结果的子域，并重复该过程，直到获得所需精度的输出为止。 该方法已经在不适定的地球物理反演问题上进行了测试，并且效果很好[9]。

历史

发明蚁群算法的人是Frans Moyson和Bernard Manderick。该领域的先驱包括Marco Dorigo，Luca Maria Gambardella[10]。

蚁群优化算法的时间顺序

  • 1959年，皮埃尔·保罗·格拉斯（ Pierre·Paul· Grassé ）发明了电光能理论 stigmergy 来解释白蚁筑巢的行为[11] ；
  • 1983年，Deneubourg及其同事研究了蚂蚁的集体行为[12]；
  • 1988年，Moyson Manderick和Moyson Manderick发表了一篇关于蚂蚁自组织的文章[13]；
  • 1989年，Goss，Aron，Deneubourg和Pasteels对阿根廷蚂蚁的集体行为进行研究，提出了蚁群优化算法的思想[14]：
  • 1989年，埃布林（Ebling）及其同事实施了食品行为模型[15]；
  • 1991年，M.Dorigo在其博士论文中提出了蚂蚁系统（该论文发表于1992年[16]）。五年后，V。Maniezzo和A. Colorni [17] 共同撰写了一篇摘自论文的技术报告；
  • 1995年，Gambardella和Dorigo提出了ant-q [18]作为蚁群系统的第一个扩展形式的蚁群系统的初始版本；
  • 1996年，Gambardella和Dorigo提出了蚁群系统[19]；
  • 1996年，发表了有关蚂蚁系统的文章[20]；
  • 1997年，Dorigo和Gambardella提出了一种通过局部搜索进行杂交的蚁群系统[21]；
  • 1998年，Dorigo发起了第一次有关ACO算法的会议[22]；
  • 1998年，Stützle提出了初始并行实施[23]；
  • 1999年，Gambardella，Taillard和Agazzi提出了macs-vrptw，这是第一个应用于带有时间窗的车辆路径问题的多蚁群系统[24]；
  • 1999年，博纳波（Bonabeau），多里戈（Dorigo）和塞拉拉兹（Theraulaz）出版了一本主要涉及人造蚂蚁的书[25]；
  • 2000年，关于蚂蚁算法的《未来计算机系统》杂志特刊出版[26]；
  • 2000年，Gutjahr提供了蚁群算法收敛的第一个证据[27]；
  • 2001年，公司（Eurobios和AntOptima）首次使用COA算法[28]；
  • 2002年，Bianchi和她的同事第一个提出了解决随机问题的算法[29]；
  • 2004年，Dorigo和Stützle与麻省理工学院出版社出版了《蚁群优化》一书[30]；
  • 2004年，Zlochin和Dorigo证明了某些算法等效于随机梯度下降，交叉熵方法和估计分布的算法[31]；
  • 2012年，Prabhakar及其同事发表了与不带信息素的串联通信的单个蚂蚁的操作有关的研究，反映了计算机网络组织的原理。该通信模型已与传输控制协议进行了比较[32]；
  • 2016年，首次应用于肽序列设计[33]；
  • 2017年，成功将多准则决策方法PROMETHEE集成到ACO算法（HUMANT算法）中[34]。

参考文献

  1. ↑ Monmarché Nicolas, Guinand Frédéric and Siarry Patrick (2010). Artificial Ants. Wiley-ISTE. ISBN 978-1-84821-194-0.
  2. ↑ A. Colorni, M. Dorigo et V. Maniezzo, Distributed Optimization by Ant Colonies, actes de la première conférence européenne sur la vie artificielle, Paris, France, Elsevier Publishing, 134-142, 1991.
  3. ↑ ,M. Dorigo, L.M. Gambardella (1997) "Ant colony system: a cooperative learning approach to the traveling salesman problem".IEEE Transactions on Evolutionary Computation,Volume: 1, Issue: 1, Apr 1997, pages 53 - 66
  4. ↑ M. Dorigo et L.M. Gambardella(1997), "Ant Colony System : A Cooperative Learning Approach to the Traveling Salesman Problem", IEEE Transactions on Evolutionary Computation, volume 1, numéro 1, pages 53-66, 1997.
  5. ↑ T. Stützle et H.H. Hoos, MAX MIN Ant System, Future Generation Computer Systems, volume 16, pages 889-914, 2000
  6. ↑ B Bullnheimer, R F Hartl, C Strauss(1997), "A new rank based version of the Ant System",Institute of Management Science
  7. ↑ X Hu, J Zhang, and Y Li (2008). "Orthogonal methods based ant colony search for solving continuous optimization problems". Journal of Computer Science and Technology, 23(1), pp.2-18.
  8. ↑ Gupta, D.K.; Arora, Y.; Singh, U.K.; Gupta, J.P., "Recursive Ant Colony Optimization for estimation of parameters of a function," Recent Advances in Information Technology (RAIT), 2012 1st International Conference on , vol., no., pp.448-454, 15–17 March 2012
  9. ↑ Gupta, D.K.; Gupta, J.P.; Arora, Y.; Shankar, U., "Recursive ant colony optimization: a new technique for the estimation of function parameters from geophysical field data," Near Surface Geophysics , vol. 11, no. 3, pp.325-339
  10. ↑ Manderick, B., Moyson, F.(1988) "The collective behavior of ants: An example of self-organization in massive parallelism",Proceedings of the AAAI Spring Symposium on Parallel Models of Intelligence. American Association of Artificial Intelligence, Stanford, CA
  11. ↑ P.-P. Grassé (1959)"La reconstruction du nid et les coordinations inter-individuelles chez Belicositermes natalensis et Cubitermes sp.",La théorie de la Stigmergie : Essai d’interprétation du comportement des termites constructeurs, Insectes Sociaux, numéro 6, p. 41-80, 1959.
  12. ↑ J.L. Denebourg, J.M. Pasteels et J.C. Verhaeghe (1985) "Probabilistic Behaviour in Ants : a Strategy of Errors?",Journal of Theoretical Biology, numéro 105, 1983.
  13. ↑ F. Moyson, B. Manderick (1988) ,The collective behaviour of Ants : an Example of Self-Organization in Massive Parallelism", Actes de AAAI Spring Symposium on Parallel Models of Intelligence, Stanford, Californie, 1988.
  14. ↑ S. Goss, S. Aron, J.-L. Deneubourg et J.-M. Pasteels(1989) ,"Self-organized shortcuts in the Argentine ant", Naturwissenschaften, volume 76, pages 579-581
  15. ↑ M. Ebling, M. Di Loreto, M. Presley, F. Wieland, et D. Jefferson(1989), An Ant Foraging Model Implemented on the Time Warp Operating System, Proceedings of the SCS Multiconference on Distributed Simulation.
  16. ↑ M. Dorigo(1992), Optimization, Learning and Natural Algorithms, PhD thesis, Politecnico di Milano, Italy.
  17. ↑ Dorigo M., V. Maniezzo et A. Colorni(1991), Positive feedback as a search strategy, rapport technique numéro 91-016, Dip. Elettronica, Politecnico di Milano, Italy.
  18. ↑ L.M. Gambardella and M. Dorigo, "Ant-Q: a reinforcement learning approach to the traveling salesman problem", Proceedings of ML-95, Twelfth International Conference on Machine Learning, A. Prieditis and S. Russell (Eds.), Morgan Kaufmann, pp. 252–260, 1995
  19. ↑ L.M. Gambardella and M. Dorigo, "Solving Symmetric and Asymmetric TSPs by Ant Colonies", Proceedings of the IEEE Conference on Evolutionary Computation, ICEC96, Nagoya, Japan, May 20-22, pp. 622-627, 1996.
  20. ↑ M. Dorigo, V. Maniezzo, et A. Colorni(1996), "Ant system: optimization by a colony of cooperating agents", IEEE Transactions on Systems, Man, and Cybernetics--Part B , volume 26, numéro 1, pages 29-41, 1996.
  21. ↑ M. Dorigo et L.M. Gambardella(1997), ["Ant Colony System : A Cooperative Learning Approach to the Traveling Salesman Problem"], IEEE Transactions on Evolutionary Computation, volume 1, numéro 1, pages 53-66, 1997.
  22. ↑ M. Dorigo, ANTS’ 98, From Ant Colonies to Artificial Ants : First International Workshop on Ant Colony Optimization, ANTS 98, Bruxelles, Belgique, octobre 1998.
  23. ↑ T. Stützle, Parallelization Strategies for Ant Colony Optimization, Proceedings of PPSN-V, Fifth International Conference on Parallel Problem Solving from Nature, Springer-Verlag, volume 1498, pages 722-731, 1998.
  24. ↑ L.M. Gambardella, E. Taillard, G. Agazzi, "MACS-VRPTW: A Multiple Ant Colony System for Vehicle Routing Problems with Time Windows", In D. Corne, M. Dorigo and F. Glover, editors, New Ideas in Optimization, McGraw-Hill, London, UK, pp. 63-76, 1999.
  25. ↑ É. Bonabeau, M. Dorigo et G. Theraulaz, Swarm intelligence, Oxford University Press, 1999.
  26. ↑ M. Dorigo , G. Di Caro et T. Stützle(2000), "Special issue on "Ant Algorithms"", Future Generation Computer Systems, volume 16, numéro 8, 2000
  27. ↑ W.J. Gutjahr(2000),"A graph-based Ant System and its convergence", Future Generation Computer Systems, volume 16, pages 873-888, 2000.
  28. ↑ . Iredi, D. Merkle et M. Middendorf(2001), "Bi-Criterion Optimization with Multi Colony Ant Algorithms", Evolutionary Multi-Criterion Optimization, First International Conference (EMO’01), Zurich, Springer Verlag, pages 359-372.
  29. ↑ L. Bianchi, L.M. Gambardella et M.Dorigo(2020), "An ant colony optimization approach to the probabilistic traveling salesman problem", PPSN-VII, Seventh International Conference on Parallel Problem Solving from Nature, Lecture Notes in Computer Science, Springer Verlag, Berlin, Allemagne.
  30. ↑ M. Dorigo and T. Stützle, Ant Colony Optimization, MIT Press, 2004.
  31. ↑ M. Zlochin, M. Birattari, N. Meuleau, et M. Dorigo, Model-based search for combinatorial optimization: A critical survey, Annals of Operations Research, vol. 131, pp. 373-395, 2004.
  32. ↑ B. Prabhakar, K. N. Dektar, D. M. Gordon(2010), "The regulation of ant colony foraging activity without spatial information ", PLOS Computational Biology.
  33. ↑ Zaidman, Daniel; Wolfson, Haim J. (2016-08-01). "PinaColada: peptide–inhibitor ant colony ad-hoc design algorithm", Bioinformatics. 32 (15): 2289–2296. ISSN 1367-4803. PMID 27153578,doi:10.1093/bioinformatics/btw133.
  34. ↑ Mladineo, Marko; Veza, Ivica; Gjeldum, Nikola (2017), "Solving partner selection problem in cyber-physical production networks using the HUMANT algorithm", International Journal of Production Research. 55 (9): 2506–2521.doi:10.1080/00207543.2016.1234084.

相关链接

编者推荐

无人机集群“圆舞曲”

蚁群优化算法Ant Colony Optimization

该书由Marco Dorigo编辑，描述了关于蚁群算法家族的理论发现，主要算法和目前应用。


10分钟搞懂蚁群算法慕课手记

笔者用比较简练的语言介绍蚁群算法，同时有python代码实战和分析。


蚁群算法创始人Prof.Marco Dorigo分享集群机器人的研究进展和成果

本课程中，蚁群算法创始人 Marco Dorigo将介绍布鲁塞尔自由大学人工智能实验室IRIDIA所做的集群机器人研究项目，以及其参与的两个欧洲研究项目的主要成果，让同类和异类集群机器人从行为上和思维上合作，执行若干不同的任务。通过课程可以更加深入了解集群算法的应用。


本中文词条由许菁参与编译，木子二月鸟总审校，费米子编辑，欢迎在讨论页面留言。

本词条内容源自wikipedia及公开资料，遵守 CC3.0协议。

取自“https://wiki.swarma.org/index.php?title=蚁群算法&oldid=2370”