后门准则
为何需要后门准则
在因果图中,我们往往需要估计变量[math]\displaystyle{ X }[/math]对另一个变量[math]\displaystyle{ Y }[/math]的因果效应,而因果图结构往往非常复杂,后门准则是用来快速估计因果图中的变量[math]\displaystyle{ X }[/math]对另一个变量[math]\displaystyle{ Y }[/math]的因果效应的判断准则,是因果推断中使用非常广泛的准则。
后门准则定义
给定有向无环图中的一对有序变量[math]\displaystyle{ (X,Y) }[/math],如果变量集合[math]\displaystyle{ Z }[/math]满足:[math]\displaystyle{ Z }[/math]中没有[math]\displaystyle{ X }[/math]的后代节点,且[math]\displaystyle{ Z }[/math]阻断了[math]\displaystyle{ X }[/math]与[math]\displaystyle{ Y }[/math]之间的每条含有指向[math]\displaystyle{ X }[/math]的路径,则称[math]\displaystyle{ Z }[/math]满足关于[math]\displaystyle{ (X,Y) }[/math]的后门准则。
如果变量集合[math]\displaystyle{ Z }[/math]满足[math]\displaystyle{ (X,Y) }[/math]的后门准则,那么X对Y的因果效应可以对变量[math]\displaystyle{ Z }[/math]的校正得到,即对[math]\displaystyle{ Z }[/math]进行求和,具体表现如下: [math]\displaystyle{ P(Y=y|do(X=x)) = \sum_zP(Y=y|X=x, Z=z)P(Z=z) }[/math]
后门准则背后逻辑
当试图寻找[math]\displaystyle{ X }[/math]对[math]\displaystyle{ Y }[/math]的因果效应时,后门准则主要有两个目的:
- 阻断任何含有指向[math]\displaystyle{ X }[/math]的后门路径/伪路径;
- 确保现在所有从变量[math]\displaystyle{ X }[/math]到变量[math]\displaystyle{ Y }[/math]的路径不变。
注意,伪路径是指与期望的从变量[math]\displaystyle{ X }[/math]指向变量[math]\displaystyle{ Y }[/math]路径不同的所有其他路径。
为了确保第一个目的,条件节点集合不能包含变量[math]\displaystyle{ X }[/math]的后代节点,因为在进行评估[math]\displaystyle{ X }[/math]对变量[math]\displaystyle{ Y }[/math]的因果效应时,会对变量[math]\displaystyle{ X }[/math]采取干预,继而影响变量[math]\displaystyle{ X }[/math]的后代节点,从而影响变量[math]\displaystyle{ Y }[/math],但以[math]\displaystyle{ X }[/math]的后代节点为条件会阻断这些路径。
为了确保第二个目的,我们需要阻断所有一切伪路径以及条件节点集合中引入的新的伪路径。 寻找一个条件节点集合使得能阻断任何含有指向[math]\displaystyle{ X }[/math]的后门路径(指可能使得[math]\displaystyle{ X }[/math]和[math]\displaystyle{ Y }[/math]相关但并不传递X产生的因果效应),因为如果不阻断这些后门路径,它们会混淆[math]\displaystyle{ X }[/math]对[math]\displaystyle{ Y }[/math]的效应。
后门准则实例
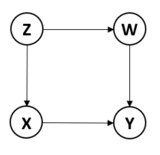
图1:[math]\displaystyle{ X }[/math]:新药;[math]\displaystyle{ Y }[/math]:痊愈率;[math]\displaystyle{ W }[/math]:体重;[math]\displaystyle{ Z }[/math]:经济社会地位
在图1的因果图中,我们搜索满足从X到Y后门准则的观察变量,可以发现,节点[math]\displaystyle{ W }[/math](非[math]\displaystyle{ X }[/math]的后代)阻断了指向[math]\displaystyle{ X }[/math]的后门路路径[math]\displaystyle{ X\leftarrow Z \rightarrow W \rightarrow Y }[/math],但没有创造新的后门路径或者改变从X到Y的有向路径,因此节点W满足后门准则,因此,只要校正W就能得到X到Y的因果效应,即
[math]\displaystyle{ P(Y=y|do(X=x)) = \sum_wP(Y=y|X=x, W=w)P(W=w) }[/math]
在寻找满足后门准则的节点集合时,需要特别关注对撞节点。
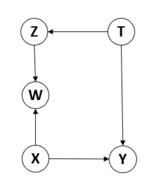
图2
在图2中,没有存在从[math]\displaystyle{ Y }[/math]到[math]\displaystyle{ X }[/math]的伪路径。但是,如果节点集合中包含对撞节点W,则打开了路径[math]\displaystyle{ X\rightarrow W \leftarrow Z\leftarrow T\rightarrow Y }[/math],该路径不是从[math]\displaystyle{ X }[/math]到[math]\displaystyle{ Y }[/math]的因果路径,因此是伪路径,打开这条路径会产生偏差并导致错误的答案。这也意味着,对[math]\displaystyle{ W }[/math]的每个值分别计算[math]\displaystyle{ X }[/math]和[math]\displaystyle{ Y }[/math]的关联性,不会得到[math]\displaystyle{ X }[/math]对[math]\displaystyle{ Y }[/math]的因果效应,甚至对于[math]\displaystyle{ W }[/math]的每个值计算[math]\displaystyle{ X }[/math]和[math]\displaystyle{ Y }[/math]的关联性也是错误的。
那么,当指定[math]\displaystyle{ W }[/math]为一个确定值[math]\displaystyle{ w }[/math]时,如何计算[math]\displaystyle{ X }[/math]对[math]\displaystyle{ Y }[/math]的因果效应?解决方法是选择其他变量来阻断由[math]\displaystyle{ W }[/math]打开的路径。例如,选择变量[math]\displaystyle{ T }[/math]为条件,仍可阻断[math]\displaystyle{ X\leftarrow Z \rightarrow W \rightarrow Y }[/math],因此,为了计算[math]\displaystyle{ w }[/math]-特定因果效应[math]\displaystyle{ P(y|do(x),w) }[/math],可以对变量[math]\displaystyle{ T }[/math]进行校正,
[math]\displaystyle{ P(Y=y|do(X=x), W=w) = \sum_tP(Y=y|X=x, W=w,T=t)P(T=t|X=x, W=w) }[/math]
[math]\displaystyle{ w }[/math]-特定因果效应[math]\displaystyle{ P(y|do(x),w) }[/math]检验[math]\displaystyle{ X }[/math]对[math]\displaystyle{ Y }[/math]的因果效应依据[math]\displaystyle{ W }[/math]值的变化而改变。
有时候,对对撞节点的校正是不可避免的。
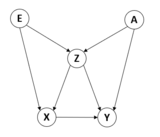
在图3中,从[math]\displaystyle{ X }[/math]到[math]\displaystyle{ Y }[/math]有四条后门路径,而且都经过[math]\displaystyle{ Z }[/math]节点,其中[math]\displaystyle{ Z }[/math]节点在路劲[math]\displaystyle{ X\leftarrow E \rightarrow Z \leftarrow A \rightarrow Y }[/math]中是一个对撞节点,以[math]\displaystyle{ Z }[/math]为条件会导致这条路径联通。因为,要阻断所有后门路径,需要至少包含一个下面集合变量中[math]\displaystyle{ \{Z, A, \} }[/math]。