工具变量
工具变量是与do演算不同的联系干预层和观测层的一种方法,它通过在观测层模拟随机控制试验来得到干预层的信息,从而实现因果效应估计,它在计量经济学、流行病学中被普遍应用。尽管do演算能够计算出所有可识别的因果效应,但是对于不可识别的情况,do演算无法把干预层表达式变形为观测层表达式。此时,如果满足一定条件,工具变量也许可以发挥作用。[1]
"它能帮助我们揭示do演算无法揭示的因果信息"。[2]——Judea Pearl
"虽然关于工具变量集得识别问题超越了do演算的应用范畴,但我们仍然可以借助因果图来解决这个问题"。[2]——Judea Pearl
工具变量概念
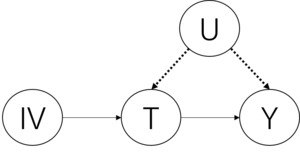
当我们在研究干预变量(治疗变量)对于结果变量(解释变量)的影响时,如果干预变量和结果变量存在不可观测的共同原因,即存在混杂因子,那么干预变量对于结果变量的因果效应是不可识别的。此时,可以通过随机对照实验去混杂,可以引入干预变量和结果变量之间可观测的中介变量去混杂,当满足下列条件时,也可以通过其他变量(工具变量)去混杂:
(1)工具变量与混杂因子相互独立,不存在因果箭头
(2)工具变量与干预变量高度相关,存在工具变量指向干预变量的因果箭头
(3)工具变量与结果变量相互独立,不存在因果箭头
(4)因果机制满足线性假设(或单调性假设)
于是,线性模型下干预变量T对于结果变量Y的因果效应强度系数β为
β=cov(IV(i),Y(i))/cov(IV(i),T(i))
应用案例
1853-1854年,英格兰爆发了霍乱疫情。霍乱是一种由霍乱细菌引起,主要通过水源传播的疾病,但是当时,人们此一无所知,一种具有竞争力的观点认为霍乱是由某种不可观测的“瘴气”引起该疾病,而且“瘴气”会污染水源。John Snow研究的是水源对于霍乱的影响,“瘴气”是混杂因子,供水公司是工具变量,但他并非有意识的使用工具变量。
1928年,遗传学家Sewall Green Wright的父亲经济学家Philippe Wright写的论文讨论亚麻籽油供给的弹性问题,即研究供应对价格的影响和价格对供应的影响,需求是混淆因子,他引入了亚麻籽每英亩的可变产量作为工具变量。
在临床试验的未履行问题(noncompliance)中,消胆胺服用是干预变量,胆固醇水平是结果变量,药物分配是工具变量,混杂因子可能是身体状况等。
孟德尔随机化是工具变量的另一种衍生版本。
代码实现
DAGitty:www.dagitty.net/dags.html
BayesiaLab:www.bayesia.com
参考文献
- ↑ https://cosx.org/2013/08/causality6-instrumental-variable
- ↑ 2.0 2.1 Pearl, Judea, and Dana Mackenzie. The book of why: the new science of cause and effect. Basic books, 2018.