后门准则
为何需要后门准则
在结构因果图中,我们往往需要估计变量[math]\displaystyle{ X }[/math]对另一个变量[math]\displaystyle{ Y }[/math]的因果效应,而结构因果图也随着图中节点数量的增加变得异常复杂,进一步加大了因果效应估计的难度。在计算[math]\displaystyle{ X }[/math]对[math]\displaystyle{ Y }[/math]的因果效应时,我们必须保证排除一切存在与变量[math]\displaystyle{ X }[/math]与[math]\displaystyle{ Y }[/math]之间的虚假关系,即非[math]\displaystyle{ X }[/math]对[math]\displaystyle{ Y }[/math]的因果途径,同时保持变量[math]\displaystyle{ X }[/math]与[math]\displaystyle{ Y }[/math]的因果途径完好无缺。换言之,寻找一个条件节点集合[math]\displaystyle{ \mathbf{Z} }[/math]使得能阻断任何含有指向[math]\displaystyle{ X }[/math]的后门路径(指可能使得[math]\displaystyle{ X }[/math]和[math]\displaystyle{ Y }[/math]相关但并不传递X产生的因果效应),因为如果不阻断这些后门路径,它们会混淆[math]\displaystyle{ X }[/math]对[math]\displaystyle{ Y }[/math]的因果效应。而后门准则就是用于快速寻找节点集合[math]\displaystyle{ \mathbf{Z} }[/math]的有效判断准则, 是结构因果图在实际应用中使用最广泛的基础准则之一。
定义
给定有向无环图中的一对有序变量[math]\displaystyle{ (X,Y) }[/math],如果变量集合[math]\displaystyle{ \mathbf{Z} }[/math]满足:
- [math]\displaystyle{ \mathbf{Z} }[/math]中没有[math]\displaystyle{ X }[/math]的后代节点;
- [math]\displaystyle{ \mathbf{Z} }[/math]阻断了[math]\displaystyle{ X }[/math]与[math]\displaystyle{ Y }[/math]之间的每条[math]\displaystyle{ X }[/math]的后门路径和伪路径,则称[math]\displaystyle{ \mathbf{Z} }[/math]满足关于[math]\displaystyle{ (X,Y) }[/math]的后门准则。
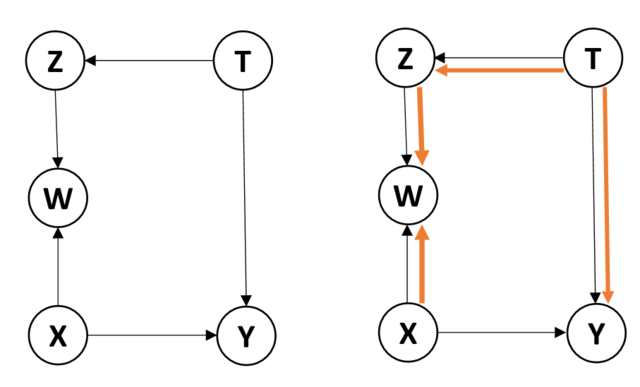
注意:有序变量[math]\displaystyle{ (X,Y) }[/math]的后门路径指在变量[math]\displaystyle{ X }[/math]和[math]\displaystyle{ Y }[/math]之间的任何指向[math]\displaystyle{ X }[/math]的路径,而伪路径指所有其他既不是[math]\displaystyle{ X }[/math]指向[math]\displaystyle{ Y }[/math]的因果路径、也不是指向[math]\displaystyle{ X }[/math]的后门路径、但会连通变量[math]\displaystyle{ X }[/math]与[math]\displaystyle{ Y }[/math]的其他路径,如图2中的以变量[math]\displaystyle{ W }[/math]为条件打开的[math]\displaystyle{ X\rightarrow W \leftarrow Z\leftarrow T\rightarrow Y }[/math]路径。
第一个条件是为了确保条件节点集合不能包含变量[math]\displaystyle{ X }[/math]的后代节点,因为在进行评估[math]\displaystyle{ X }[/math]对变量[math]\displaystyle{ Y }[/math]的因果效应时,会对变量[math]\displaystyle{ X }[/math]采取干预,继而影响变量[math]\displaystyle{ X }[/math]的后代节点,从而影响变量[math]\displaystyle{ Y }[/math],但以[math]\displaystyle{ X }[/math]的后代节点为条件会阻断这些路径。第二个条件是为了阻断所有一切伪路径以及条件节点集合引入的新伪路径。
如果变量集合[math]\displaystyle{ \mathbf{Z} }[/math]满足[math]\displaystyle{ (X,Y) }[/math]的后门准则,那么[math]\displaystyle{ X }[/math]对[math]\displaystyle{ Y }[/math]的因果效应可以对变量集[math]\displaystyle{ \mathbf{Z} }[/math]的校正得到,即对[math]\displaystyle{ \mathbf{Z} }[/math]中所有变量进行概率求和,具体计算如下:
[math]\displaystyle{ P(Y=y|do(X=x)) = \sum_zP(Y=y|X=x, \mathbf{Z}=z)P(\mathbf{Z}=z) }[/math]
后门准则实例
实例1
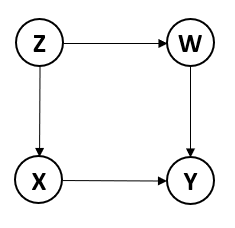
试图获取药物[math]\displaystyle{ X }[/math]对痊愈率[math]\displaystyle{ Y }[/math]的因果效应,同时还测量了对痊愈率有影响的体重[math]\displaystyle{ W }[/math]。另外,我们知道经济社会地位[math]\displaystyle{ Z }[/math]同时影响患者体重和患者对接受治疗的选择,但是在这个研究中并没有关于经济社会地位的统计数据。
在图1的因果图中包含四个变量[math]\displaystyle{ X }[/math]、[math]\displaystyle{ Y }[/math]、[math]\displaystyle{ W }[/math]、[math]\displaystyle{ Z }[/math]四个变量,现在我们估计变量[math]\displaystyle{ X }[/math]对变量[math]\displaystyle{ Y }[/math]的因果效应,即搜索满足有向变量对[math]\displaystyle{ (X,Y) }[/math]的后门准则的变量集合。不难发现,节点[math]\displaystyle{ W }[/math](非[math]\displaystyle{ X }[/math]的后代)阻断了指向[math]\displaystyle{ X }[/math]的后门路径[math]\displaystyle{ X\leftarrow Z \rightarrow W \rightarrow Y }[/math],但没有创造新的后门路径或者改变从[math]\displaystyle{ X }[/math]到变量[math]\displaystyle{ Y }[/math]的有向路径,因此单个节点[math]\displaystyle{ W }[/math]满足后门准则,因此,只要校正[math]\displaystyle{ W }[/math]就能得到从变量[math]\displaystyle{ X }[/math]到变量[math]\displaystyle{ Y }[/math]的因果效应,即
[math]\displaystyle{ P(Y=y|do(X=x)) = \sum_wP(Y=y|X=x, W=w)P(W=w) }[/math]
实例2
在寻找满足后门准则的节点集合时,需要特别关注对撞节点。
在图2中,当节点集合为空集时,没有存在从[math]\displaystyle{ Y }[/math]到[math]\displaystyle{ X }[/math]的后门路径。但是,如果节点集合中包含对撞节点[math]\displaystyle{ W }[/math],则打开了路径[math]\displaystyle{ X\rightarrow W \leftarrow Z\leftarrow T\rightarrow Y }[/math](图中黄色路径),该路径不是从[math]\displaystyle{ X }[/math]到[math]\displaystyle{ Y }[/math]的因果路径也不是后门路径,但是伪路径,打开这条路径会产生偏差并导致错误的估计。这也意味着,对[math]\displaystyle{ W }[/math]的每个值分别计算[math]\displaystyle{ X }[/math]和[math]\displaystyle{ Y }[/math]的关联性,不会得到[math]\displaystyle{ X }[/math]对[math]\displaystyle{ Y }[/math]的因果效应,甚至对于[math]\displaystyle{ W }[/math]的每个值计算[math]\displaystyle{ X }[/math]和[math]\displaystyle{ Y }[/math]的关联性也是错误的。
那么,当指定[math]\displaystyle{ W }[/math]为一个确定值[math]\displaystyle{ w }[/math]时,如何计算[math]\displaystyle{ X }[/math]对[math]\displaystyle{ Y }[/math]的因果效应?解决方法是选择其他变量来阻断由[math]\displaystyle{ W }[/math]打开的路径。例如,选择变量[math]\displaystyle{ T }[/math]为条件,仍可阻断[math]\displaystyle{ X\rightarrow W \leftarrow Z\leftarrow T\rightarrow Y }[/math],因此,为了计算[math]\displaystyle{ w }[/math]-特定因果效应[math]\displaystyle{ P(y|do(x),w) }[/math],可以对变量[math]\displaystyle{ T }[/math]进行校正:
[math]\displaystyle{ P(Y=y|do(X=x), W=w) = \sum_tP(Y=y|X=x, W=w,T=t)P(T=t|X=x, W=w) }[/math]
[math]\displaystyle{ w }[/math]-特定因果效应[math]\displaystyle{ P(y|do(x),w) }[/math]表明[math]\displaystyle{ X }[/math]对[math]\displaystyle{ Y }[/math]的因果效应依据[math]\displaystyle{ W }[/math]值的变化而改变。
实例3
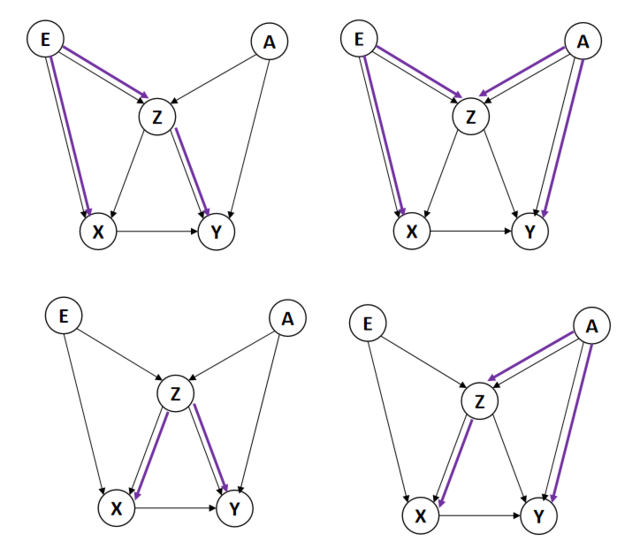
在某些因果图中,校正对撞节点有时候是不可避免的,如图3所示。
在图3中,从[math]\displaystyle{ X }[/math]到[math]\displaystyle{ Y }[/math]有四条后门路径(图中紫色路径),而且都经过[math]\displaystyle{ Z }[/math]节点。在路径[math]\displaystyle{ X\leftarrow E \rightarrow Z \leftarrow A \rightarrow Y }[/math]中, 变量[math]\displaystyle{ Z }[/math]节点是一个对撞节点,以[math]\displaystyle{ Z }[/math]为条件会导致这条路径联通。因此,要阻断所有四条后门路径,可以选择包含变量[math]\displaystyle{ Z }[/math]的变量集合,如[math]\displaystyle{ \{Z,A \} }[/math]、[math]\displaystyle{ \{Z,E \} }[/math]、[math]\displaystyle{ \{Z,A,E \} }[/math]。
实例4 - 辛普森悖论
为了确定药物在人群中的有效性,设想一种假设性的干预措施,即对整个人群统一服用这种药物,并与补充干预下的痊愈率进行比较,补充干预指阻止每个人服用药物。用[math]\displaystyle{ do(X=1) }[/math]表示第一种干预,用[math]\displaystyle{ do(X=0) }[/math]表示第二种干预,现在要估计它们的差异:
[math]\displaystyle{ P(Y=y|do(X=1)) - P(Y=y|do(X=0)) }[/math]
在没有因果关联的情况下,无法从数据集本身估计因果效应,这就是辛普森悖论的教训,数据本身甚至不足以确定药物的作用是正面的还是负面的。但是借助图4的因果图模型,可以从数据中计算因果效应的大小。为此,以对图进行处理的形式模拟干预,即对模型中全体人群都服用了该药物。
| 患者服药情况 | 患者未服药情况 | |||
|---|---|---|---|---|
| 患者 | 痊愈患者数 | 痊愈率/% | 痊愈患者数 | 痊愈率/% |
| 男性患者 | 81例(共87例) | 93 | 234例(共270例) | 87 |
| 女性患者 | 192例(共263例) | 73 | 55例(共80例) | 69 |
| 合计 | 273例 (共350例) | 78 | 289例(共350例) | 83 |
[math]\displaystyle{ \begin{alignat}{3}
P(Y=1|do(X=1)) & = \sum_Z P(Y=1|X=1, Z=z)P(Z) \\
& = P(Y=1|X=1, Z=1)P(Z=1) + P(Y=1|X=1, Z=0)P(Z=0) \\
&= \frac{0.93*(87+270)}{700} + \frac{0.73*(263+80)}{700} = 0.832 \\
\end{alignat}
}[/math]
同理,
[math]\displaystyle{ \begin{alignat}{3} P(Y=1|do(X=0)) & = \sum_Z P(Y=1|X=0, Z=z)P(Z) \\ & = P(Y=1|X=0, Z=1)P(Z=1) + P(Y=1|X=0, Z=0)P(Z=0) \\ & = \frac{0.87*(87+270)}{700} + \frac{0.69*(263+80)}{700} = 0.781 \end{alignat} }[/math]
因此,服用药物的效果和不服用药物的效果的差异为:
[math]\displaystyle{ \begin{alignat}{3} P(Y=1|do(X=1)) - P(Y=1|do(X=0)) & = 0.832 - 0.781 \\ & = 0.0502 \end{alignat} }[/math]