图灵机

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
SyouTK（讨论 | 贡献）2021年8月20日 (五) 15:43的版本
跳到导航 跳到搜索

图灵机是一种数学计算模型，定义了一个抽象的机器，该机器可以根据指定的规则表在纸带上进行操作。虽然图灵机模型非常简单，但是图灵机可以模拟任何给定的计算机算法。

图灵机在一条无限长的纸带上运行，纸带被分割成若干个离散的单元格。机器的读写头在一个单元格上“读取”或“扫描”纸带上的符号。然后，图灵机根据读取的符号和机器自身在用户指定指令的“有限表”中的状态，机器(i)在单元格中写下一个符号（例如，有限字母表中的数字或字母），然后(ii)将纸带向左或向右移动一个单元，然后(iii)根据观察到的符号和机器自身在表中的状态，要么继续执行另一指令，要么停止计算。

图灵机是1936年由阿兰·图灵（Alan Turing）发明，他称之为“自动机”。通过这个模型，图灵能够否定地回答两个问题:

是否存在一台机器，能够确定其纸带上的任意机器是否是“循环”的(例如，死机，或无法继续其计算任务) ?
是否存在一种机器可以确定其纸带上的任何任意机器是否曾经打印出一个特定的符号？

因此，通过提供可以进行任意计算的非常简单的装置的数学描述，他能够证明计算的一般性质，尤其是判定性问题(翻译自德语Entscheidungsproblem, 英文译作decision problem)的不可计算性。

图灵机证明了机械计算能力存在基本限制。虽然机械计算可以表达任意的计算，但最小设计使机械计算不适合在实践中计算: 与图灵机不同的是，现实世界的计算机是基于另外一种设计，即使用随机存取存储器 （Random-access memory）。

图灵完备性（Turing completeness）是一个指令系统模拟图灵机的能力。一个图灵完备的编程语言理论上能够表达所有计算机可以完成的任务; 如果忽略有限内存的限制，几乎所有的编程语言都是图灵完备的。

图灵机概述

图灵机是一种中央处理器单元（Central Processing Unit，即CPU），控制着计算机的所有数据操作，规范及其使用顺序内存来存储数据。更具体的，图灵机是一种能够枚举字母表有效字符串的机器（自动机）;这些字符串是字母递归可枚举集的一部分。理想情况下，图灵机有无限长的纸带，其可以在上面执行读写操作。

假设有一个“黑盒子”，图灵机无法知道它最终是否会用给定的程序枚举出子集中的任何一个特定字符串。这是因为停机问题（Halting Problem）是不可解的，停机问题对计算的理论极限有着重大的影响。

图灵机能够处理不受限制的语法，这意味着它能够以无限多的方式鲁棒地评价一阶逻辑。通过λ运算可以证明这一点。

能够模拟任何其他图灵机的图灵机称为通用图灵机。邱奇（Alonzo Church，美国著名数学家）提出了一个更具有普适性的数学定义。他将在λ运算的工作和图灵在正式计算机理论中的工作融合，称为邱奇-图灵理论。在这项工作中，他指出图灵机确实抓住了逻辑和数学中有效方法的非正式概念，并提供了算法或“机械程序”的精确定义。研究它们的抽象特性可以使我们对计算机科学和复杂性理论有更深入的了解。

物理描述

在1948年的论文《智能机器（Intelligent Machinery）》中，图灵写道他的机器包括: 以无限长纸带的形式获得的无限存储容量，纸带上标有方块，每个方块上可以打印一个符号。在任何时候，机器中都有一个符号，被称为扫描符号。机器可以改变扫描的符号，其行为部分由该符号决定，但纸带上其他地方的符号不会影响机器的行为。然而，纸带可以在机器中来回移动，这是机器的基本操作之一。因此，纸带上的任何符号最终都可能有一个局。

描述

图灵机在纸带上进行机械操作的机器进行数学建模。纸带上有符号，机器可以使用读写头一次一个读取和写入这些符号。操作完全由一组有限的基本指令决定，例如“在状态42中，如果看到的符号为0，则写入1；如果看到的符号为1，则改为状态17；在状态17中，如果看到的符号为0，写一个1并更改为状态6”等。在原始的文章中（“论可计算的数字，以及对可判定行的影响”）。图灵想象的不是一种机制，而是一种他被称之为计算机的“人”，可以严格执行这些决定性的机械规则的人。

更切确地说，图灵机由以下部分组成:

  • 纸带。纸带被分成多个单元，每个紧邻着。每个单元都包含来自某个有限字母表的一个符号。字母表中包含有一个特殊的空白符号（此处写作“0”）和一个或者多个其他符号。假设纸带可以任意向左/向右扩展，所以图灵机拥有能够支撑起计算所需的纸带数量。没有写入过的单元格被假定用空白符号填充。在某些型号中，胶带的左端标有特殊符号，磁带向右侧延伸或无限延伸。
  • 读写头。读写头可以在纸带上读写符号，并一次将纸带左右移动一个（有且仅有一个）单元格。在某些型号的机器中，读写头移动而纸带静止。
  • 状态寄存器。状态寄存器用来存储图灵机的状态，是有限多个状态中的一个。其中有一个特殊的启动状态，状态寄存器就是用它来初始化。图灵写道，这些状态代替了执行计算的人通常会处于的 "精神状态"。
  • 一个有限的指令表[1][2]，给定机器当前所处的状态(qi)和它在纸带上读取的符号(aj)（当前读写头下的符号），告诉机器依次做以下事情（对于5元组模型）：
  1. 擦除或写入一个符号（将aj替换为aj1）。
  2. 移动读写头（由dk描述，如果值为'L'表示向左移动一步，'R'表示向右移动一步，'N'表示停留在原地）。
  3. 假设与规定的状态相同或新的状态（进入状态qi1）

在四元组模型中，擦除或写入符号（aj1)）和向左或向右移动读写头（dk）被指定为独立的指令。该表告诉机器（ia）擦除或写入一个符号，或者（ib）向左或向右移动读写头，然后（ii）按规定承担相同或新的状态，但在同一指令中不能同时执行（ia）和（ib）。在某些模型中，如果表中没有当前符号和状态组合的条目，那么机器将暂停; 其他模型要求填充所有条目。

机器的每一部分（即它的状态、符号收集和在任何特定时间使用的纸带）和它的行动（如打印、擦除和纸带运动）都是有限的、离散的和可区分的；是无限的纸带和运行时间给了它无限制的存储空间。

在Hopcroft和Ullman之后，单纸带图灵机可以被正式定义为一个七元组M=⟨Q,Г,b,Σ,δ,q_0,F⟩，其中：

  • Г是有限的、非空的纸带字母符号集；
  • bᕮГ，是空白符号（唯一允许在计算过程中的任何步骤无限频繁地出现在纸带上的符号）；
  • Σ⊆Г\{b}是输入符号集，即允许出现在初始纸带内容中的符号集；
  • Q是有限的、非空的状态集；
  • q_0ᕮQ是初始状态；
  • F⊆Q是最终状态或接受状态的集合。初始纸带内容被认为是接受由M如果它最终停止在一个状态 F.
  • δ: （Q \ F) Χ Г Χ {L, R}是一个偏函数，称为转移函数，其中 L 是左移，R 是右移。如果在当前状态和当前纸带符号上未定义，则机器停止；直观地，转移函数指定了从当前状态转移的下一个状态，哪个符号覆盖读写头指向的当前符号，以及下一个读写头运动。

此外，图灵机还可以有拒绝状态，使拒绝更加明确。在这种情况下，有三种可能性：接受、拒绝和永远运行。另一种可能性是将磁带上的最终值视为输出。然而，如果唯一的输出是机器最终所处的状态（或永远不停止），机器仍然可以有效地输出一个较长的字符串，通过输入一个整数，告诉它要输出字符串的哪一位。

一个相对不常见的变体允许“无移位”，比如 N，作为方向集的第三个元素{L, R}。

三状态繁忙的海狸（busy beaver）七元组是这样的:（关于繁忙的海狸相关的资料可以搜索“图灵机实例”了解）

  • Q={A, B, C, HALT}(状态);
  • Г= {0, 1}(纸带符号);
  • b=0（空白符号）；
  • Σ={1}（输入符号）；
  • q_0 = A（初始状态）；
  • F={HALT}（最终状态）；
  • δ=参见下面的状态表（转换函数）。

空白的时候，所有的纸带单元格都用0标记。

State table for 3-state, 2-symbol busy beaver
纸带符号 当前状态 A 当前状态 B 当前状态 C
写入符号 移动纸带 下一个状态 写入符号 移动纸带 下一个状态 写入符号 移动纸带 下一个状态
0 1 R B 1 L A 1 L B
1 1 L C 1 R B 1 R 停机

可视化或实现图灵机所需的其他细节

用Van Emde Boas（1990）的话来说: “集合论对象（类似于上面的七元组描述形式）只提供了关于机器将如何运行以及它的计算将是什么样子的部分信息。”

例如，

  • 符号到底是什么样子的，需要有很多决策，也需要有一种万无一失的方法来无穷尽地读写符号。
  • 左移和右移操作可能会使读写头在纸带上移动，但在实际构建图灵机时，更实际的做法是让纸带在读写头下来回滑动。
  • 纸带可以是有限的，并根据需要自动延伸出空白（这是最接近数学定义的），但更常见的是将其视为在一端或两端无限延伸，除了读写头所在的明确给定的有限片段外，都会被预先填充空白。(当然，这在实践中是无法实现的。)纸带的长度不能是固定的，因为那不符合给定的定义，而且会严重限制机器可以执行的计算范围，如果纸带与输入大小成正比，则为线性有界自动机的计算范围，如果纸带是严格的固定长度，则为有限状态机的计算范围。

其他定义

文献中的定义有时会稍有不同，以使论证或证明更容易或更清晰，但这总是以使所产生的机器具有相同的计算能力的方式进行。例如，集合可以从 [math]\displaystyle{ \{L,R\} }[/math] 改为 [math]\displaystyle{ \{L,R,N\} }[/math]其中N("无 "或 "无操作")将允许机器停留在同一纸带单元上，而不需要左右移动。这样不会增加机器的计算能力。

最常见的规则是根据图灵/戴维斯的规则，在“图灵表”钟永9个5元组中的一个表示每个“图灵指令”（图灵1936年在《The Undecidable》p.126-127）： （定义1） ：（(qi, Sj, Sk/E/N, L/R/N, qm)） 其中qi,是当前状态，Sj是已扫描符号，Sk是打印符号，E是擦除，N是无状态，L是向左移动，R是向右，qm 是新状态。

其他作者(Minsky，Hopcroft和Ullman，Stone采用了另一种规定，在扫描符号Sj之后立即列出新状态qm: (定义2): (qi, Sj, qm, Sk/E/N, L/R/N)

（当前状态 qi , 扫描符号 Sj , 新状态 qm , 打印 Sk/擦除 E/none N , L/right R/none N）

其中qi,是当前状态，Sj是已扫描符号，Sk是打印符号，E是擦除，N是无状态，L是向左移动，R是向右，qm 是新状态。

文的其余部分将使用“定义1”(图灵/戴维斯规则)。

例子: 将3状态2符号“繁忙的海狸”简化为5元组

例子: 将3状态2符号“繁忙的海狸”简化为5元组

当前状态

扫描符号

打印符号

移动纸带

最终（即下一个）状态

5元组

A 0 1 R B (A, 0, 1, R, B)
A 1 1 L C (A, 1, 1, L, C)
B 0 1 L A (B, 0, 1, L, A)
B 1 1 R B (B, 1, 1, R, B)
C 0 1 L B (C, 0, 1, L, B)
C 1 1 N H (C, 1, 1, N, H)

在下表中，图灵的原始模型只允许前三行，他称之为N1, N2, N3(参见图灵书籍《The Undecidable》p.126）。他允许通过命名第0个S0="E"或"N"，即“擦除”或者“空白”等。但是，他不允许“不打印”，所以每个指令行都包括“打印符号Sk”或者“擦除E”。这些缩写是图灵在1936-1937年的原始论文之后，机器模型已经允许所有九种可能的五元组类型。

当前的m配置
(（图灵状态）

纸带符号

打印

纸带运动

最终的M配置
（图灵状态）

5元组

5元组注释

4元组

N1 qi Sj 打印(Sk) 向左 L qm (qi, Sj, Sk, L, qm) "blank" = S0, 1=S1, etc.
N2 qi Sj 打印(Sk) 向右 R qm (qi, Sj, Sk, R, qm) "blank" = S0, 1=S1, etc.
N3 qi Sj 打印(Sk) 空 N qm (qi, Sj, Sk, N, qm) "blank" = S0, 1=S1, etc. (qi, Sj, Sk, qm)
4 qi Sj 空 N 向左 L qm (qi, Sj, N, L, qm) (qi, Sj, L, qm)
5 qi Sj 空 N 向右 R qm (qi, Sj, N, R, qm) (qi, Sj, R, qm)
6 qi Sj None N None N qm (qi, Sj, N, N, qm) Direct "jump" (qi, Sj, N, qm)
7 qi Sj 擦除 向左 L qm (qi, Sj, E, L, qm)
8 qi Sj 擦除 向右 R qm (qi, Sj, E, R, qm)
9 qi Sj 擦除 空 N qm (qi, Sj, E, N, qm) (qi, Sj, E, qm)

任何图灵表（指令列表）都可以由上述九个5元组构成。由于技术原因，三个非打印或 "N "指令（4、5、6）通常可以省去。

较少遇到使用4元组的情况：这些代表了图灵指令的进一步原子化（参见Post(1947)，Boolos & Jeffrey(1974，1999)，Davis-Sigal-Weyuker(1994)）；

状态

图灵机上下文中使用的“状态”一词可能会引起混淆，因为它可能意味着两件事。图灵之后的大多数研究者都使用“状态”来表示要执行的当前指令的名称/指示符——即状态寄存器的内容。但是图灵 (1936) 在他所谓的机器“m-配置”的记录和机器（或人）通过计算的“进展状态”——整个系统的当前状态——之间做出了强有力的区分。图灵所说的“状态公式”包括当前指令和纸带上的所有符号：

因此，任何阶段的计算进度状态完全由指令注释和纸带上的符号决定。也就是说，系统的状态可以由单个表达式（符号序列）来描述，该表达式由纸带上的符号后跟 Δ（我们假设不会出现在其他地方）和指令注释组成。这个表达式被称为“状态公式”。——《The Undecidable》,图灵，p.139–140

更早时期，图灵在他的论文中进行了进一步的研究：他举了一个例子，在该示例中，他把当前 "m-配置 "的符号（指令的标签）和纸带上的所有符号一起放在扫描的方块下面（《The Undecidable》，第121页）；他把这个称为"完整的配置"（《The Undecidable》，第118页）。为了将 "完整配置 "打印在一行，他将状态标签/m-配置放在扫描符号的左边。

在Kleene（1952）中可以看到这样的一个变体，Kleene展示了如何写出一台机器的 "状态"的哥德尔数：他把 "m-配置 "符号q4放在磁带上6个非空白方格的大致中心的扫描方格上(见本文图灵-纸带图)，并把它放在扫描方格的右边。但Kleene把 "q4 "本身称为 "机器状态"（Kleene，第374-375页）。Hopcroft和Ullman把这种组合称为 "瞬时描述"，并遵循图灵规定，把 "当前状态"（指令标签，m-配置）放在扫描符号的左边（第149页）。

示例：3次“移动”后，三态2符号繁忙的海狸的总状态（取自下图中的示例“运行”）：

1A1

这意味着：经过三次移动后，纸带上有......000110000......，读写头正在扫描最右边的1，状态为A。空白（在这种情况下用 "0 "表示）可以成为总状态的一部分，如图所示。B01；纸带上有一个 "1"，但读写头正在扫描它左边的 "0"（"空白"），状态是B。

图灵机情况中，应阐明 "状态 "是哪种状态。(i)当前指令，或(ii)纸带上的符号列表连同当前指令，或(iii)纸带上的符号列表连同当前指令放在扫描符号的左边或扫描符号的右边。

图灵的传记作者Andrew Hodges (1983:107)注意到并讨论了这种混淆。

图灵机的状态图

繁忙的海狸的表格("P" = 打印/写入 a "1")

纸带符号

当前状态A

当前状态B

当前状态C

写入符号

移动纸带

下一个状态

写入符号

移动纸带

下一个状态

写入符号

移动纸带

下一个状态

0 P R B P L A P L B
1 P L C P R B P R 停机

“三态繁忙的海狸”图灵机的有限状态表示。每个圆圈代表表的一个“状态”——一个“m-配置”或“指令”。状态转换的"方向"用箭头表示。出状态附近的标签（如0/P,R）（在箭头的“尾部”）指定了引起特定转换的扫描符号（如0），后面是斜线/，接着是机器的后续“行为”，如“P打印”然后移动纸带“R向右”。没有普遍接受的格式存在。所显示的规则是以McClusky（1965）、Booth（1967）、Hill和Peterson（1974）为蓝本。

右边：上面的表格表示为“状态转换”图。

通常大的表格最好是留作表格（Booth，p.74）。它们更容易由计算机以表格形式模拟出来（Booth，p.74）。然而，某些概念，例如具有“复位”状态的机器和具有重复模式的机器（参见Hill和Peterson p.244）在被视为图纸时更容易被看到。

图纸是否代表了对其表的改进，必须由读者针对特定的情况来决定。详见有限状态机。

繁忙的海狸的计算进化从顶部开始，一直到底部。

再次提醒读者，这种图表示的是在时间上冻结的表的快照，而不是计算在时间和空间上的过程(“轨迹”)。虽然繁忙的海狸的机器每次“运行”都会遵循相同的状态轨迹，但对于可以为变量输入“参数”提供信息的“复制”机器而言，情况并非如此。

“计算进度 "图显示了三态繁忙的海狸从开始到结束的计算过程中的“状态”（指令）进度。最右边是每一步的图灵“完整配置”。如果机器停止并清空“状态寄存器”和整个纸带，则可以使用这些“配置”在其进行中的任何地方重新启动计算（参见Turing（1936）The Undecidable 第139– 140页）。

图灵机的等价模型

许多可能被认为比简单的通用图灵机有更多计算能力的机器，实际上并没有更多的能力（Hopcroft和Ullman p.159, cf. Minsky(1967)）。它们可能计算得更快，或者使用更少的内存，或者它们的指令集可能更小，但是它们不能计算更多的数学函数。（邱奇-图灵理论假设这对任何机器都是正确的：任何可以被“计算”的东西都可以被某些图灵机器计算。）

图灵机相当于单堆栈下推自动机（Pushdown Automaton，PDA），它通过放宽其栈中的“后进先出”要求，使其更加灵活和简洁。此外，通过使用一个堆栈对读写头左侧的纸带进行建模，使用另一个堆栈对读写头右侧的磁带进行建模，图灵机也等效于具有标准“后进先出”语义的双堆栈PDA。

在另一个极端，一些非常简单的模型变成了图灵等价模型，即具有与图灵机模型相同的计算能力。

常见的等价模型是多带图灵机、多道图灵机、有输入和输出的机器，以及与确定型图灵机（Deterministic Turing Machine，DTM）和非确定型图灵机（non-Deterministic Turing Machine , NDTM）(NDTM) ，后者的动作表对于每个符号和状态组合最多只有一个条目。

只读、右移动的图灵机相当于 DFAs（以及通过使用 NDFA 到 DFA 转换算法转换的 NFA）。

对于实际的和教学的意图，等价的 寄存器机器可以作为通常的汇编编程语言使用。

一个有趣的问题是：用具体编程语言表示的计算模型是否是图灵等价的？虽然真实计算机的计算是基于有限状态的，因此无法模拟图灵机，但编程语言本身并不一定具有这种限制。Kirner等人在2009年的研究表明，在通用编程语言中，有些语言是图灵完备的，而有些则不是。例如，ANSI C并不等同于图灵机，因为ANSI C的所有实例（由于标准出于遗留的原因，故意不定义某些行为，所以可以有不同的实例）都意味着有限空间的内存。这是因为内存引用数据类型的大小，称为指针，可以在语言内部访问。然而，其他编程语言，如Pascal，则没有这个功能，这使得它们在原则上是图灵等价的。只是原则上是图灵等价的，因为编程语言中的内存分配是允许失败的，也就是说，当忽略失败的内存分配时，编程语言可以是图灵等价的，但在真实计算机上可执行的编译程序却不能。

选择C型机器、Oracle的O型机器

早在1936年的论文中，图灵就对“运动......完全由配置决定”的“自动机”和“选择机”进行了区分： 它的运动只是部分由配置决定…当这样一台机器达到其中一种不明确的配置时，它不能继续运行，直到外部操作者做出任意的选择。如果我们使用机器来处理公理系统，就会出现这种情况。——The Undecidable，p.118

图灵(1936)除了在脚注中描述了如何使用自动机来“找到所有希尔伯特微积分的可证明公式”，而不是使用选择机之外，没有做进一步的说明。他"假设选择总是在0和1之间。那么每个证明将由i1, i2, ..., in (i1 = 0 或 1, i2 = 0 或 1, ..., in = 0 或 1) 的选择序列决定，因此数字 2n + i12n-1 + i22n-2 + ... +in 完全决定了证明。自动机依次执行验证1、验证2、验证3，……”

这通过这种技术，一个确定型的（比如，a-）图灵机可以用来模拟一个非确定型的图灵机的行为; 图灵在脚注中解决了这个问题，似乎把它从进一步的考虑中剔除了。

Oracle机或o-machine是一种图灵机器，它将计算暂停在“o”状态，同时，为了完成计算，它“等待”“oracle”——一个未指定的实体（不是一台机器）“的决定（The undecutable，p.166-168）。

通用图灵机

图灵机的实现

正如图灵在《The Undecidable》一书中所写，第128页： 我们可以发明一种机器，用来计算任何可计算序列。如果向机器U提供纸带，纸带的开头写着计算机M用分号隔开的五元数组，那么机器U将计算出与机器M相同的序列。

虽然这一发现现在被认为是很常见的，但在当时（1936年），很多人认为这是不可思议的。图灵称之为“通用机器”（缩写为“U”）的计算模型被一些人（参见Davis(2000)）认为是产生存储程序计算机概念的基础理论的突破。

实质上包含了现代计算机的发明以及伴随着它的一些编程技术。——Minsky（1967），P.104

就计算复杂度而言，多带通用图灵机与它所模拟的机器相比，只需要慢上一个对数倍。这个结果是由F.C.Hennie和R.E.Stearns在1966年得到的。(Arora and Barak，2009，定理1.9)

与实际机器的比较

使用乐高积木实现的图灵机（Lego pieces）

人们常说，图灵机不同于简单的自动机，它和实际的机器一样强大，能够执行真实程序所能执行的任何操作。在这种说法中被忽略的是，由于实际的机器只能有有限的配置，所以这里的“真正的机器”其实只是一个有限的状态机。另一方面，图灵机相当于拥有无限存储空间进行计算的机器。

有很多方法可以解释为什么图灵机是实际计算机的有用模型:

  1. 凡是真正的计算机能计算的东西，图灵机也能计算。例如，“图灵机可以模拟编程语言中的任何类型的子程序，包括递归程序和任何已知的参数传递机制”（Hopcroft and Ullman 第157页）。一个足够大的FSA也可以模拟任何真正的计算机，而不用考虑IO。因此，关于图灵机的局限性的说法也将适用于实际计算机。
  2. 区别只在于图灵机有能力处理无限制的数据量。然而，在有限的时间内，图灵机（像实际的机器）只能操纵处理的数据量。
  3. 像图灵机一样，实际的机器可以根据需要，通过获得更多的磁盘或其他存储介质，扩大其存储空间。
  4. 使用较简单的抽象模型对真机程序的描述往往比使用图灵机的描述要复杂得多。例如，描述算法的图灵机可能有几百个状态，而给定实际机器上的等效确定性有限自动机（deterministic finite automaton，DFA）却有四千亿个状态。这使得DFA的表示方式无法分析。
  5. 图灵机描述的算法与它们使用的内存多少无关。目前任何机器所拥有的内存都有一个极限，但这个极限可以在时间上任意上升。图灵机允许我们对算法做出声明，这些声明（理论上）将永远成立，而不考虑传统计算机架构的进步。
  6. 图灵机简化了算法的表述。在图灵机上运行的算法通常比在实际机器上运行的算法更通用，因为它们有任意精度的数据类型可用，而且永远不必处理意外情况（包括但不限于内存耗尽）。

图灵机的局限性

计算复杂性理论

图灵机的一个局限性在于，其不能很好地模拟特定排列的优势。例如，现代存储程序计算机实际上是一种更具体的抽象机器的实例，这种抽象机器被称为随机存取存储程序机器或 RASP机器模型。与通用图灵机一样，RASP将其“程序”存储在有限状态机的“指令”之外的“内存”中。与通用图灵机不同的是，RASP具有无限数量可区分的、有编号但无限制的“寄存器”——可以包含任何整数的内存“单元”（参见Elgot和Robinson(1964)，Hartmanis(1971)，特别是Cook-Rechow(1973)）；RASP的有限状态机可以间接寻址（例如，一个寄存器的内容可以用作另一个寄存器的地址），因此当图灵机被用作约束运行时间的基础时，可以证明某些算法的运行时间有一个“假下限”（由于图灵机的假简化假设）。这方面的一个例子是二进制搜索，当使用RASP计算模型而不是图灵机模型时，可以证明这种算法的运行速度更快。

并发性

图灵机的另一个局限是，其不能很好地模拟并发。例如，一个始终保持非确定性的图灵机在空白纸带上开始计算的整数大小是有限制的。相比之下，有一些没有输入的始终保持一致的并发系统，可以计算出无界大小的整数。(可以用本地存储创建一个初始化为0的进程，它同时向自己发送一个“停止”和一个“运行”的消息。当它收到一个“运行”信息时，它的计数增加1，并向自己发送一个去信息。当它收到一个“停止”消息时，它就停止，在它的本地存储区有一个无限制的数字）。

交互

在计算机的早期，计算机的使用通常仅限于批处理，即非交互式任务，每个任务从给定的输入数据中产生输出数据。可计算性理论研究从输入到输出的函数的可计算性，图灵机就是为此而发明的，其反映了这种做法。

自20世纪70年代以来，计算机的交互式使用变得更加普遍。原则上，可以通过让外部代理与图灵机同时从纸带中读出并写入纸带的方式进行建模，但这很少与交互的实际发生方式相吻合；因此，在描述交互性时，通常首选I/O自动机等替代程序。

历史

历史背景：计算机器

罗宾•甘迪（Robin Gandy，1919-1995）是图灵（1912-1954）的学生，也是他一生的朋友，他将“计算机器”这一概念的渊源追溯到查尔斯•巴贝奇（Charles Babbage）（大约1834年），并提出了“巴贝奇论”： 整个发展和分析的操作现在都可以由机器来执行。（italics in Babbage as cited by Gandy, p.54）

甘迪对巴贝奇分析机的分析描述了以下五种操作:

  1. 算术函数+，-，×，其中“-”表示“适当的”减法，即满足某种条件，比如y≥x，x-y=0。
  2. 任何运算序列都是一个运算。
  3. 操作的迭代（重复n次操作p）。
  4. 条件迭代（以测试t的“成功”为条件重复n次操作p）。
  5. 条件转移（即有条件的“goto”）。

Gandy指出: “可由(1)、(2)和(4)计算出来的函数恰恰是那些图灵可计算的函数。”(p.53)。他引用了其他关于“通用计算机”的理论，包括珀西·卢德盖特（Percy Ludgate， 1909年）、莱昂纳多·托雷斯·奎维多（Leonardo Torres y Quevedo，1914年）、莫里斯·d’奥卡涅（Maurice d'Ocagne，1922年）、路易斯·库夫尼纳尔（Louis Couffignal，1933年）、万尼瓦尔·布什V（annevar Bush，1936年）、霍华德·艾肯（Howard Aiken，1937年）。然而: 重点是对一个固定的可迭代的算术运算序列进行编程。条件性迭代和条件性转移对于计算机的一般理论的根本重要性没有得到承认……——Gandy，第55页

判定问题: 希尔伯特1900年提出的第10号问题

关于著名数学家大卫·希尔伯特（David Hilbert）在1900年提出的希尔伯特问题中，第10号问题的一个方面浮动了近30年，才被准确地框定下来。希尔伯特对10号问题的原始表述如下： 10. Diophantine方程的可解性的确定。给出一个具有任意数量的未知量和有理积分系数的Diophantine方程。设计一个过程，根据这个过程可以在有限的操作中确定该方程是否可以用有理整数来解。当我们知道一个程序，允许任何给定的逻辑表达式通过有限的多次操作来决定其有效性或可满足性时，判定问题（一阶逻辑的决定问题）就解决了……判定问题必须被认为是数理逻辑的主要问题。——2008年，德尔肖维茨（Dershowitz）和古列维奇（Gurevich）引用了此译文和德文原文

到了1922年，“判定问题”的概念有了进一步的发展，Behmann指出： 判定问题的一般形式如下:需要一个相当明确的、普遍适用的处方，它将允许人们在有限的步骤中决定一个给定的纯逻辑论断的真假……——Gandy，第57页，引用Behmann的话

Behmann指出：一般问题相当于决定哪些数学命题是真的问题。如果能够解决判定问题，那么人们就会有一个“解决许多（甚至所有）数学问题的程序”。

1928年的国际数学家大会，希尔伯特把他的问题描述的非常的细致。第一，数学是完整的吗？第二，数学是一致的吗？第三，数学是可判定的吗？”1930年，在希尔伯特发表退休演讲的同一次会议上，库尔特·哥德尔（Kurt Gödel）回答了前两个问题；而第三个问题（判定问题）不得不等到上世纪30年代中期。

问题在于，要回答这个问题，首先需要对“明确的通用规则”下一个精确定义。普林斯顿大学的教授阿朗佐•丘奇（Alonzo Church）将其称为“有效可计算性”，而在1928年并不存在这样的定义。但在接下来的6-7年里，埃米尔•波斯特（Emil Post）拓展了他的定义，即一个工人按照一张指令表从一个房间移动到另一个房间书写和擦除标记（1936），邱奇和他的两个学生斯蒂芬·克莱恩（Stephen Kleene）和（j.B. Rosser）利用邱奇的λ微积分和哥德尔的递归理论也是如此。丘奇的论文（发表于1936年4月15日）表明，判定问题确实是“无法决策的”，比图灵早了将近一年（图灵的论文1936年5月28日提交，1937年1月发表）。与此同时，波斯特在1936年秋天提交了一篇短文，所以图灵至少比波斯特更有优先权。当丘奇评审图灵的论文时，图灵有时间研究丘奇的论文，并在附录中添加了一个草图，证明邱奇的λ微积分和他的机器可以计算同样的函数。

但邱奇所做的是完全不同的事情，而且在某种意义上是较差的。……图灵的构造更直接，并提供了最初原则的论据，从而弥补了邱奇证明中的空白。——Hodges，第112页

波斯特只是提出了一个可计算性的定义，并批评了邱奇的“定义”，但没有证明任何事情。

阿兰图灵的机器

1935年春天，图灵作为英国剑桥大学国王学院的一名年轻硕士生，接受了这个挑战；他受到逻辑学家纽曼（Newman）的讲座的鼓舞，并从他们那里了解了哥德尔的工作和判定问题。在图灵1955年的讣告中，纽曼写道: 对于“什么是'机械'过程”？图灵回答了一个特有的答案“可以由机器完成的事情”，接着他开始着手分析计算机的一般概念。——Gandy，第74页

Gandy表示： 我想，但我不知道，图灵从他工作的一开始，就把证明判定问题的不可解性作为他的目标。1935年夏天，他告诉我，当他躺在格兰切斯特草地的时候，他完成了这篇论文的构想。这个“构想”可能是他对计算的分析，也可能是他意识到有一个普遍的机器，因此有一个对角线论证来证明不可解性。——同上，第76页

尽管Gandy认为Newman的上述言论有“误导性”，但这一观点并不为所有人所认同。图灵一生都对机器有着浓厚的兴趣：“阿兰（图灵）从小就梦想发明打字机；（他的母亲）图灵夫人有一台打字机；他很可能一开始就问自己，把打字机称为‘机械的’是什么意思”（Hodges p.96）。在普林斯顿攻读博士学位时，图灵制造了一个布尔逻辑乘法器（见下文）。他的博士论文题为“基于序数的逻辑系统”，包含了“可计算函数”的定义： 上面说过，“如果一个函数的值可以通过某种纯粹的机械过程找到，那么它就是有效的可计算的”。我们可以从字面上理解这句话，用纯粹的机械过程来理解可以由机器来完成的过程。我们有可能以某种正常形式对这些机器的结构进行数学描述。这些想法的发展导致了作者对可计算函数的定义，以及对可计算性与有效可计算性的认同。要证明这三个定义（第三个是λ-微积分）是等价的并不困难，虽然有些麻烦。——图灵（1939）在《The Undecidable》一书中，第160页

当图灵回到英国后，他负责破解名为“英格玛”的加密机创造的德国密码；他还参与了ACE（自动计算引擎）的设计。“图灵的ACE建议实际上是自成一体的，其根源不在于EDVAC（美国的倡议），而在于他自己的通用机器”（Hodges p.318）。关于被Kleene（1952年）命名为 “图灵论文”的起源和性质的争论仍在继续。但是，图灵用他的计算机模型所证明的东西出现在他的论文中“On Computable Numbers, with an Application to the Entscheidungsproblem”。

希尔伯特-判定问题不可能有解……因此我建议，不可能有一个一般的过程来确定函数微积分K的一个给定公式U是否可证明，也就是说，不可能有一台机器在提供任何一个公式U的情况下，最终会说出U是否可证明。——摘自图灵的论文，详见《The Undecidable》，第145页

图灵的例子（他的第二个证明）：如果有人要求用一般程序来告诉我们：“这台机器是否曾经打印过0”，这个问题就是“无法确定的”。

1937-1970“数字计算机”“计算机科学”的诞生

1937年，图灵在普林斯顿大学写博士论文时，从零开始建立了一个数字（布尔逻辑）乘法器，自制了机电继电器（Hodges p.138）。“艾伦的任务是将图灵机的逻辑设计体现在一个由继电器操作的开关网络中……”（Hodges p.138）。德国（Konrad Zuse，1938年）和美国（Howard Aiken，1937年）都在朝着同一个方向努力，他们的劳动成果被轴心国和盟国的军队在二战中使用。在20世纪50年代初至中期，Hao Wang和Marvin Minsky将图灵机简化为一种更简单的形式（它是 Martin Davis的后图灵机的前身）；与此同时，欧洲研究人员将这种新型电子计算机简化为一种类似于计算机的理论物体，相当于现在所说的“图灵机”。在20世纪50年代后期和60年代初期，Melzak和Lambek（1961）、Minsky（1961）和Shepherdson and Sturgis（1961）等人不约而同地展开进一步的研究，推进了欧洲的工作，并将图灵机简化为一个更友好的、类似计算机的抽象模型，称为计数器；Elgot和Robinson（1964）、 Hartmanis（1971）、Cook 和 Reckhow（1973）将这项工作进一步推进到寄存器和随机存取机器模型——但基本上所有这些都只是带有类似算术指令集的多带图灵机。

1970年至今：作为计算模型的图灵机

如今，计数器、寄存器和随机存取机以及它们的先驱图灵机仍然是理论家们研究计算理论问题的首选模型。特别是，计算复杂性理论也使用了图灵机。

根据人们在计算中喜欢操作的对象(非负整数或字母数字串等)，有两种模型在基于机器的复杂性理论中获得了主导地位： 离线多带图灵机——它代表了面向字符串计算的标准模型，以及Cook和Reckhow提出的随机存取机(RAM) ，它是理想化的冯诺依曼式计算机的模型。——van Emde Boas 1990:4 只有在算法分析的相关领域，这个角色才能被RAM模型所取代。——van Emde Boas 1990:4

另参见

  • 算术层次结构
  • 贝肯斯坦约束，表明不可能出现有限大小和有限能量的无限带图灵机。
  • BlooP 和 FlooP（这是两种编程语言）
  • 繁忙的海狸
  • Chaitin常数或Omega（计算机科学）以获取有关停止问题的信息。
  • 中文房间
  • 康威生命游戏，一个图灵完备的细胞自动机
  • 数字无限
  • 皇帝的新脑
  • 枚举器（理论计算机科学）
  • 遗传
  • 哥德尔、艾舍尔、巴赫——集异璧之大成，这是一本讨论邱奇-图灵论等话题的名著。
  • 停机问题
  • 哈佛结构
  • 命令式编程
  • 朗顿蚂蚁和白蚁，图灵机的二维模型
  • 修正后的哈佛结构
  • 概率图灵机
  • 随机存取图灵机
  • 量子图灵机
  • 香农，另一位信息理论的领军科学家
  • 图灵机实例
  • 调协开关
  • 图灵图谱，任何计算系统或语言，尽管是图灵完备的，但通常被认为对实际计算无用。
  • 无组织的机器，图灵关于神经网络的早期想法
  • 冯-诺依曼结构

笔记

  1. ↑ Occasionally called an action table or transition function.
  2. ↑ Usually quintuples [5-tuples]: qiaj→qi1aj1dk, but sometimes quadruples [4-tuples].

参考文献

原始文献、重印和汇编

  • B. Jack Copeland (ed.)(2004), The Essential Turing: Seminal Writings in Computing, Logic, Philosophy, Artificial Intelligence, and Artificial Life plus The Secrets of Enigma, Clarendon Press (Oxford University Press), Oxford UK. Contains the Turing papers plus a draft letter to Emil Post re his criticism of "Turing's convention", and Donald W. Davies' Corrections to Turing's Universal Computing Machine
  • Martin Davis (mathematician)|Martin Davis (ed.) (1965), The Undecidable, Raven Press, Hewlett, NY.
  • Emil Post (1936), "Finite Combinatory Processes—Formulation 1", Journal of Symbolic Logic, 1, 103–105, 1936. Reprinted in The Undecidable, pp. 289ff.
  • Emil Post (1947), "Recursive Unsolvability of a Problem of Thue", Journal of Symbolic Logic, vol. 12, pp. 1–11. Reprinted in The Undecidable, pp. 293ff. In the Appendix of this paper Post comments on and gives corrections to Turing's paper of 1936–1937. In particular see the footnotes 11 with corrections to the universal computing machine coding and footnote 14 with comments on Turing's proof|Turing's first and second proofs.
  • Turing, A.M. (1936). "On Computable Numbers, with an Application to the Entscheidungsproblem". Proceedings of the London Mathematical Society. 2 (published 1937). 42: 230–265. doi:10.1112/plms/s2-42.1.230. (and Turing, A.M. (1938). "On Computable Numbers, with an Application to the Entscheidungsproblem: A correction". Proceedings of the London Mathematical Society. 2 (published 1937). 43 (6): 544–6. doi:10.1112/plms/s2-43.6.544.). Reprinted in many collections, e.g. in The Undecidable, pp. 115–154; available on the web in many places.
  • Alan Turing, 1948, "Intelligent Machinery." Reprinted in "Cybernetics: Key Papers." Ed. C.R. Evans and A.D.J. Robertson. Baltimore: University Park Press, 1968. p. 31. Reprinted in Turing, A. M. (1996). "Intelligent Machinery, A Heretical Theory". Philosophia Mathematica. 4 (3): 256–260. doi:10.1093/philmat/4.3.256.
  • F. C. Hennie and R. E. Stearns. Two-tape simulation of multitape Turing machines. JACM, 13(4):533–546, 1966.

可计算性理论

  • Boolos, George; John Burgess; Richard Jeffrey (2002). Computability and Logic (4th ed.). Cambridge UK: Cambridge University Press. ISBN 0-521-00758-5.  Some parts have been significantly rewritten by Burgess. Presentation of Turing machines in context of Lambek "abacus machines" (cf. Register machine) and Computable function|recursive functions, showing their equivalence.
  • Taylor L. Booth (1967), Sequential Machines and Automata Theory, John Wiley and Sons, Inc., New York. Graduate level engineering text; ranges over a wide variety of topics, Chapter IX Turing Machines includes some recursion theory.
  • Martin Davis (1958). Computability and Unsolvability. McGraw-Hill Book Company, Inc, New York.  On pages 12–20 he gives examples of 5-tuple tables for Addition, The Successor Function, Subtraction (x ≥ y), Proper Subtraction (0 if x < y), The Identity Function and various identity functions, and Multiplication.
  • Davis, Martin; Ron Sigal; Elaine J. Weyuker (1994). Computability, Complexity, and Languages and Logic: Fundamentals of Theoretical Computer Science (2nd ed.). San Diego: Academic Press, Harcourt, Brace & Company. ISBN 0-12-206382-1. 
  • Hennie, Fredrick (1977). Introduction to Computability. Addison–Wesley, Reading, Mass. QA248.5H4 1977. . On pages 90–103 Hennie discusses the UTM with examples and flow-charts, but no actual 'code'.
  • John Hopcroft and Jeffrey Ullman (1979). Introduction to Automata Theory, Languages, and Computation (1st ed.). Addison–Wesley, Reading Mass. ISBN 0-201-02988-X.  Centered around the issues of machine-interpretation of "languages", NP-completeness, etc.
  • Hopcroft, John E.; Rajeev Motwani; Jeffrey D. Ullman (2001). Introduction to Automata Theory, Languages, and Computation (2nd ed.). Reading Mass: Addison–Wesley. ISBN 0-201-44124-1.  Distinctly different and less intimidating than the first edition.
  • Stephen Kleene (1952), Introduction to Metamathematics, North–Holland Publishing Company, Amsterdam Netherlands, 10th impression (with corrections of 6th reprint 1971). Graduate level text; most of Chapter XIII Computable functions is on Turing machine proofs of computability of recursive functions, etc.
  • Knuth, Donald E. (1973). Volume 1/Fundamental Algorithms: The Art of computer Programming (2nd ed.). Reading, Mass.: Addison–Wesley Publishing Company. . With reference to the role of Turing machines in the development of computation (both hardware and software) see 1.4.5 History and Bibliography pp. 225ff and 2.6 History and Bibliographypp. 456ff.
  • Zohar Manna, 1974, Mathematical Theory of Computation. Reprinted, Dover, 2003.
  • Marvin Minsky, Computation: Finite and Infinite Machines, Prentice–Hall, Inc., N.J., 1967. See Chapter 8, Section 8.2 "Unsolvability of the Halting Problem." Excellent, i.e. relatively readable, sometimes funny.
  • Christos Papadimitriou (1993). Computational Complexity (1st ed.). Addison Wesley. ISBN 0-201-53082-1.  Chapter 2: Turing machines, pp. 19–56.
  • Hartley Rogers, Jr.Theory of Recursive Functions and Effective Computability, The MIT Press, Cambridge MA, paperback edition 1987, original McGraw-Hill edition 1967 (pbk.)
  • Stone, Harold S. (1972). Introduction to Computer Organization and Data Structures (1st ed.). New York: McGraw–Hill Book Company. ISBN 0-07-061726-0. 
  • Peter van Emde Boas 1990, Machine Models and Simulations, pp. 3–66, in Jan van Leeuwen, ed., Handbook of Theoretical Computer Science, Volume A: Algorithms and Complexity, The MIT Press/Elsevier (Volume A). QA76.H279 1990. Valuable survey, with 141 references.

丘奇的论文

  • Roger Penrose (1990) [1989]. The Emperor's New Mind (2nd ed.). Oxford University Press, New York. 

小型图灵机

  • Todd Rowland, 2007, "Confusion on FOM", Wolfram Science message board, October 30, 2007.

其他

  • Martin Davis (2000). Engines of Logic: Mathematicians and the origin of the Computer (1st ed.). W. W. Norton & Company, New York. 
  • Robin Gandy, "The Confluence of Ideas in 1936", pp. 51–102 in Rolf Herken, see below.
  • Stephen Hawking (editor), 2005, God Created the Integers: The Mathematical Breakthroughs that Changed History, Running Press, Philadelphia. Includes Turing's 1936–1937 paper, with brief commentary and biography of Turing as written by Hawking.
  • Rolf Herken (1995). The Universal Turing Machine—A Half-Century Survey. Springer Verlag. ISBN 978-3-211-82637-9. 
  • Andrew Hodges, Alan Turing: The Enigma, Simon and Schuster, New York. Cf. Chapter "The Spirit of Truth" for a history leading to, and a discussion of, his proof.
  • Roger Penrose, The Emperor's New Mind: Concerning Computers, Minds, and the Laws of Physics, Oxford University Press, Oxford and New York, 1989 (1990 corrections).
  • Hao Wang (academic)|Hao Wang, "A variant to Turing's theory of computing machines", Journal of the Association for Computing Machinery (JACM) 4, 63–92 (1957).
  • Arora, Sanjeev; Barak, Boaz, "Complexity Theory: A Modern Approach", Cambridge University Press, 2009, section 1.4, "Machines as strings and the universal Turing machine" and 1.7, "Proof of theorem 1.9"
  • Kantorovitz, Isaiah Pinchas (December 1, 2005). "A note on turing machine computability of rule driven systems". SIGACT News. 36 (4): 109–110. doi:10.1145/1107523.1107525.

外部链接

编者推荐

集智文章推荐

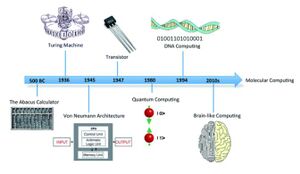
1931年，天才数学家图灵提出了著名的图灵机模型，它奠定了人工智能的数学基础。1943年，麦克洛克 & 皮茨（McCulloch & Pitts）两人提出了著名的人工神经元模型，该模型一直沿用至今，它奠定了所有深度学习模型的基础。那么，这两个开山之作究竟是怎样一种相爱相杀的关系呢？天才数学家冯诺依曼指出，图灵机和神经元本质上虽然彼此等价，我们可以用图灵机模拟神经元，也可以用神经元模拟图灵机，但是它们却位于复杂度王国中的不同领地。神经网络代表了一大类擅长并行计算的复杂系统，它们自身的结构就构成了对自己最简洁的编码；而图灵机则代表了另一类以穿行方式计算的复杂系统，这些系统以通用图灵机作为复杂度的分水岭：一边，系统的行为可以被更短的代码描述；另一边，我们却无法绕过复杂度的沟壑。而先进的深度学习研究正在试图将这两类系统合成为一个：神经图灵机。

课程推荐

本课程将围绕图灵机，详细介绍图灵机的定义、图灵机的计算、图灵机框架的模拟、通用图灵机、以及图灵停机问题，说明算法的上界。
本课程为北京师范大学系统科学学院张江教授开设的研究生课程《人工智能》课程回放。课程偏重理论，辅以编程实践，将粗粒度的梳理人工智能重要的理念、算法、模型。前面会包含一些人工智能之前的理论计算机模型，图灵机等，后面系统从两方面讲解，一是符号派的人工智能，包括搜索、推理、表示等；二是连接派的人工智能，机器学习，强调理论机器学习基础。

文章推荐

为了顺应快速增长的信息存储和处理需求，需要新的计算策略。分子计算的想法（即通过分子、超分子或生物分子方法进行基本计算，而不是通过电子方法）长期以来一直吸引着研究人员。使用分子和(生物)大分子进行计算的前景并非没有先例。自然中充满了以高效率、低能量成本和高密度信息编码来处理和存储数据的示例。根据通用计算方法运行的计算机的设计和组装，例如图灵机中的计算机，未来可能会以化学的方式实现。从这个角度来看，本文章重点介绍了到目前为止已经设计和合成的分子和(生物)大分子系统，目的是将它们用于计算目的；还提出了分子图灵机的蓝图，它基于一个催化装置，它沿着聚合物带滑动，在移动时，以氧原子的形式在这条带上打印二进制信息。
展示现代计算技术和未来分子计算的发现和进展的时间表.jpg
尽管阿兰·图灵(Alan Turing)在1952年发表的关于形态发生的论文中提出了常微分方程的反应扩散模型，反映了他对数学生物学的兴趣，但他从未被认为接近过细胞自动机的定义。然而，他对形态发生的处理，特别是他发现的与对称破缺导致的某些形式的不均匀分布有关的困难，是将他的普遍计算理论与他的生物模式形成理论联系起来的关键。建立这样的联系并不能克服图灵所担心的特殊困难，无论如何，这个问题已经在生物学上得到了解决。但相反，这里开发的方法抓住了图灵最初关心的问题，并通过算法概率的概念为更一般的问题提供了一个低级解决方案，从而将图灵模式形成和通用计算这两个他对科学最重要的贡献联系在了一起。本文将展示使用此方法的一维模式的实验结果，而不会损失对n维模式泛化的一般性。

本中文词条由Moonscar、Solitude、Langenfeng、Swarma编译，AvecSally、ZQ及用户SyouTK审校，编辑，如有问题，欢迎在讨论页面留言。

本词条内容源自wikipedia及公开资料，遵守 CC3.0协议。

取自“https://wiki.swarma.org/index.php?title=图灵机&oldid=25995”