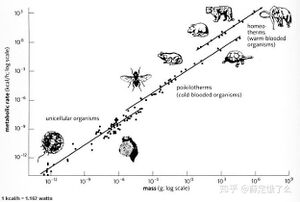
克莱伯定律

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
栗子CUGB（讨论 | 贡献）2021年9月18日 (六) 00:00的版本
(差异) ←上一版本 | 最后版本 (差异) | 下一版本→ (差异)
跳到导航 跳到搜索

克莱伯定律（Kleiber's law）根据观测数据提出，对于很多动物，其基础代谢率水平与体重的¾次幂成正比，该定律得名于1930年代早期马克斯·克莱伯(Max Kleiber)的生物学著作。若用符号表示，设q0为该动物的代谢率，M是其重量，则q0 ~ M¾。因此一般一只猫的重量是一只老鼠的100倍，那么它的代谢量比老鼠约大31倍。而在植物中，指数则接近于1。

克莱伯定律中指数的确切值尚不清楚，部分是因为对于该定律当前没有令人完全满意的理论解释。

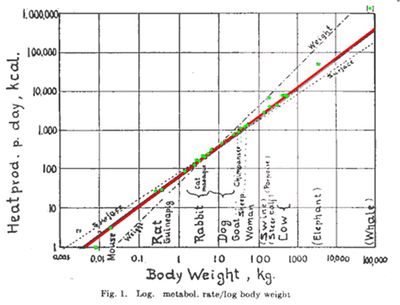
Figure 1. 一些物种的体型与代谢率的曲线[1]。最先发表于克莱伯(1947)。

定律背后的原因

克莱伯定律，像许多其他的异速生长律定律一样，是物理学和/或动物循环系统几何学的结果[2]。马克思·克莱伯在分析物种内大量独立个体的呼吸时首先发现这一定律[3]。克莱伯想要找到2⁄3 的指数（原因解释如下），但是被他发现的3⁄4的指数所迷惑[4]。

启发式解释

对克莱伯定律的一个解释是结构质量和增长质量之间的区别。结构质量涉及维护成本，而储备质量不涉及。所以，一个物种的小成体比另一个物种的大成体每单位重量的呼吸量大，因为它们的身体质量中有更大的部分是结构成分而不是储备成分。 在每个物种内，年轻的（即小的）生物体比同一物种的年老的（大的）生物体每单位重量的呼吸量大，这是由于生长的间接成本所致[5]。

指数2/3

2/3的解释——人们倾向于认为，新陈代谢率的变化是为了避免热衰竭。因为身体通过表面被动地散热，但在整个质量上通过新陈代谢产生热量，所以新陈代谢率必须以这样指数的方式来抵消平方-立方法则。这种方式的精确指数是2/3[6]。

这样的论证并没有解决不同的生物体表现出不同的形状（因此即使是按相同的尺寸缩放也有不同的表面积与体积比）这个事实。对生物体表面积的合理估计似乎确实和新陈代谢率成线性比例关系[5]。

指数3/4

根据一些学者的研究，克莱伯定律像许多其他的异速生长律定律一样，是动物循环系统物理学和几何学特性的结果。同一物种中，年轻的个体比年老的个体每份重量的呼吸消耗更多，因为它们体重中中组织结构的比例更大，而储能的比例较小。结构质量需要耗费养护能量，而储能的质量则不需要。

韦斯特、因奎斯特和布朗（以下简称WEB）的一个模型表明，3/4标度的产生是因为营养物质在整个生物体内分配和运输的效率。在大多数生物体中，新陈代谢是由具有分支管的循环系统支持的（即植物的血管系统、昆虫的器官或人类的心血管系统）[7]。

具体来说，West，Enquist和Brown提出三点假设（1）代谢率B正比于循环系统中的营养流量（即体液总流量）Q，即[math]\displaystyle{ B\propto Q }[/math]（2）体液（例如血液）总体积V正比于体重M，即[math]\displaystyle{ V \propto M }[/math]。这个假设的成立意味着循环系统中的能量耗散降至最低（3）循环系统由微管组成（例如毛细血管、肺泡）。

然后他们在最小的循环管（毛细血管、肺泡等）层面上分析了这两种说法的后果。在实验中，那些最小的小管的容积在很大的质量范围内是恒定的。循环系统中的微管尽管千差万别，但总的来说，都具有层级结构，有自相似性。因为通过一个微管的体液流量正比于微管体积，所以基础代谢率B正比于体液总流量Q，而体液总流量Q正比于微管总数N，即

[math]\displaystyle{ Q\propto N }[/math]

另一方面，体液具有不可压缩性。而循环系统不是简单地按比例放大，而是具有自相似性（假设3）。嵌套的深度取决于小管尺寸的自相似指数，而该深度的影响则取决于每个分支产生多少个“子”小管。依赖一个（非常松散的）精确的小管模型，可以将这些数值与宏观数量联系起来。WEB指出，如果我们将循环系统描述为由大大小小的圆柱连接成的系统，那么为了防止液体在小圆柱中被堵塞，就要求圆柱总数（即微管总数）{{Mvar|N}和体液总体积V满足

[math]\displaystyle{ N^4\propto V^3 }[/math][8]

再结合假设1、2，因为血量是身体质量中的固定部分，所以有

[math]\displaystyle{ B\propto M^{\frac{3}{4}} }[/math][7]

非幂律标度

更新近的研究表明克莱伯法则在大多数尺度上都不成立。对较小的动物（10公斤[22磅]以下的鸟类，或昆虫）来说，新陈代谢率通常更贴近2/3而非3/4。对较大的动物来说，情况正好相反[6]。因此，新陈代谢率与体重的对数图似乎是向上“弯曲”的，而且与二次函数模型拟合得更好[9]。在所有情况下，局部拟合出的指数在 [2/3,3/4] 之间[10]。

修改后的循环系统模型

对WBE模型所做的调整保留了网络形状的假设，它预测出更大的缩放指数，加剧了与观测数据的差异[11]。但我们可以通过放宽WBE对营养物质运输网络的假设，即这个网络既是分形的又是循环的，从而保留一个类似的理论[10]。（WBE认为，分形循环网络的发展必然会使得用于运输的能量最小化，但其他研究人员认为，他们的推导有一些潜在的错误[6][12])。不同的网络效率较低，因为它们表现出较低的缩放指数，但由营养物质运输决定的新陈代谢率将表现出2/3到3/4的缩放[10]。如果较大的新陈代谢率在进化上收到青睐，那么重量小的生物将倾向于把它们的网络安排成2/3的规模，但重量大的生物将倾向于把它们的网络安排成3/4，这就产生了观察到的曲率[13]。

修改后的热力学模型

另一个模型指出，新陈代谢率并不仅仅是为了来产生热量。只对有用功做贡献的新陈代谢率应该以指数1缩放（线性），然而对产热做贡献的新陈代谢率应该受表面积限制，并且以指数2缩放。基础代谢率是以下两种效应的凸组合：如果又用功的比例为f，那么基础代谢率的比例应该为

[math]\displaystyle{ B=f\cdot kM+(1-f)\cdot k'M^{\frac {2}{3}} }[/math]

其中k和k′是比例常数。k′特别描述了生物体的表面积比率，大约为0.1kJ·h−1·g−2/3[4]。f的典型值为15%-20%[14]。f的理论最大值为21%，因为葡萄糖的氧化效率只有42%，这样产生的ATP有一半被浪费了[4]。

实验支持

对各种物理变量的方差分析表明，尽管基础代谢率的大部分变化是由质量决定的，但其他具有显著影响的变量还包括体温和生物分类法[15][16]。

1932年，布洛迪的一项工作计算出指数大约为0.73[5][17]。

2004年，一项对哺乳动物的现场代谢率分析得出结论，它们似乎以0.749的指数作为标度[13]。

对定律的批评

Koz和Kon认为，通过任何形式的限制因素来解释克莱伯定律的尝试都是有缺陷的，因为代谢率在休息和活动之间的变化差了四五倍。因此，任何影响基础代谢率标度的限制，实际上都会使升高的代谢——以及所有的动物活动——变得不可能[18]。相反，WEB认为，动物在休息时很可能对最小的运输能量耗散进行优化，同时不放弃在其他时间的低效率运作的能力[19]。

其他研究人员也指出，Koz和Kon对该法则的批评倾向于关注WEB循环网络的精确结构细节，但后者对该模型并不重要[8]。

克莱伯法则仅在将动物当作整体研究时出现；分类学亚群内的缩放指数有很大差异[20][21]。

一般化

克莱伯定律只适用于种间比较；它（通常）不适用于种内比较[22]。

在其他界的情形

1999年，一项分析认为，在植物生长过程中，特定植物的生物量产量于与植物质量的3/4次方成比例[23]。单2001年的一篇涉及各种类型的单细胞光合生物的论文发现，比例指数介于0.75和1之间[24]。

2006年，发表在《自然》期刊上的一篇论文认为，植物幼苗的质量指数接近1，但物种、门类和生长条件之间的差异压压倒了任何类似“克莱伯定律”的影响[25]。

生物体内的结果

因为细胞原生质在一系列生物体质量中似乎具有恒定的密度，所以克莱伯定律的一个推论是，在较大的物种中，每个细胞体可获得的能量较少。细胞似乎通过选择以下两种策略之一来应对这个困难：较低的细胞代谢率，或较小的细胞。后一个策略是通过神经元和脂肪细胞表现出来的；前者是由每个其他类型的细胞表现出来的[26]。于是，不同的器官表现出不同的异质性标度（见下表）[5]。

人体组织的BMR与质量的等距标度
器官 缩放指数
大脑 0.7
肾 0.85
肝 0.87
心脏 0.98
肌肉 1.0
骨骼 1.1

参考资料

  1. ↑ Kleiber M (October 1947). "Body size and metabolic rate". Physiological Reviews. 27 (4): 511–41. doi:10.1152/physrev.1947.27.4.511. PMID 20267758
  2. ↑ Schmidt-Nielsen, Knut(1984). Scaling: Why is animal size so important?. NY, NY: Cambridge University Press. ISBN 978-0521266574.
  3. ↑ Kleiber M (1932). "Body size and metabolism". Hilgardia. 6 (11): 315–351. doi:10.3733/hilg.v06n11p315.
  4. ↑ 4.0 4.1 4.2 Ballesteros FJ, Martinez VJ, Luque B, Lacasa L, Valor E, Moya A (January 2018). "On the thermodynamic origin of metabolic scaling". Scientific Reports. 8 (1): 1448. Bibcode:2018NatSR...8.1448B. doi:10.1038/s41598-018-19853-6. PMC 5780499. PMID 29362491.
  5. ↑ 5.0 5.1 5.2 5.3 Hulbert, A. J. (28 April 2014). "A Sceptics View: "Kleiber's Law" or the "3/4 Rule" is neither a Law nor a Rule but Rather an Empirical Approximation". Systems. 2 (2): 186–202. doi:10.3390/systems2020186.
  6. ↑ 6.0 6.1 6.2 Dodds PS, Rothman DH, Weitz JS (March 2001). "Re-examination of the "3/4-law" of metabolism". Journal of Theoretical Biology. 209 (1): 9–27. arXiv:physics/0007096. doi:10.1006/jtbi.2000.2238. PMID 11237567. S2CID 9168199.
  7. ↑ 7.0 7.1 West GB, Brown JH, Enquist BJ (April 1997). "A general model for the origin of allometric scaling laws in biology". Science. 276 (5309): 122–6. doi:10.1126/science.276.5309.122. PMID 9082983. S2CID 3140271.
  8. ↑ 8.0 8.1 Etienne RS, Apol ME, Olff HA (2006). "Demystifying the West, Brown & Enquist model of the allometry of metabolism". Functional Ecology. 20 (2): 394–399. doi:10.1111/j.1365-2435.2006.01136.x.
  9. ↑ Kolokotrones T, Deeds EJ, Fontana W (April 2010). "Curvature in metabolic scaling". Nature. 464 (7289): 753–6. Bibcode:2010Natur.464..753K. doi:10.1038/nature08920. PMID 20360740. S2CID 4374163.。 But note that a quadratic curve has undesirable theoretical implications; see MacKay NJ (July 2011). "Mass scale and curvature in metabolic scaling. Comment on: T. Kolokotrones et al., curvature in metabolic scaling, Nature 464 (2010) 753-756". Journal of Theoretical Biology. 280 (1): 194–6. doi:10.1016/j.jtbi.2011.02.011. PMID 21335012.
  10. ↑ 10.0 10.1 10.2 Banavar JR, Moses ME, Brown JH, Damuth J, Rinaldo A, Sibly RM, Maritan A (September 2010). "A general basis for quarter-power scaling in animals". Proceedings of the National Academy of Sciences of the United States of America. 107 (36): 15816–20. Bibcode:2010PNAS..10715816B. doi:10.1073/pnas.1009974107. PMC 2936637. PMID 20724663
  11. ↑ Savage VM, Deeds EJ, Fontana W (September 2008). "Sizing up allometric scaling theory". PLOS Computational Biology. 4 (9): e1000171. Bibcode:2008PLSCB...4E0171S. doi:10.1371/journal.pcbi.1000171. PMC 2518954. PMID 18787686.
  12. ↑ Apol ME, Etienne RS, Olff H (2008). "Revisiting the evolutionary origin of allometric metabolic scaling in biology". Functional Ecology. 22 (6): 1070–1080. doi:10.1111/j.1365-2435.2008.01458.x.
  13. ↑ 13.0 13.1 Savage VM, Gillooly JF, Woodruff WH, West GB, Allen AP, Enquist BJ, Brown JH (April 2004). "The predominance of quarter-power scaling in biology". Functional Ecology. 18 (2): 257–282. doi:10.1111/j.0269-8463.2004.00856.x. The original paper by West et al. (1997), which derives a model for the mammalian arterial system, predicts that smaller mammals should show consistent deviations in the direction of higher metabolic rates than expected from M3⁄4 scaling. Thus, metabolic scaling relationships are predicted to show a slight curvilinearity at the smallest size range.
  14. ↑ Clarke A, Rothery P, Isaac NJ (May 2010). "Scaling of basal metabolic rate with body mass and temperature in mammals". The Journal of Animal Ecology. 79 (3): 610–9. doi:10.1111/j.1365-2656.2010.01672.x. PMID 20180875.
  15. ↑ Clarke A, Rothery P, Isaac NJ (May 2010). "Scaling of basal metabolic rate with body mass and temperature in mammals". The Journal of Animal Ecology. 79 (3): 610–9. doi:10.1111/j.1365-2656.2010.01672.x. PMID 20180875.
  16. ↑ Hayssen V, Lacy RC (1985). "Basal metabolic rates in mammals: taxonomic differences in the allometry of BMR and body mass". Comparative Biochemistry and Physiology. A, Comparative Physiology. 81 (4): 741–54. doi:10.1016/0300-9629(85)90904-1. PMID 2863065.
  17. ↑ Brody, S. (1945). Bioenergetics and Growth. NY, NY: Reinhold.
  18. ↑ Kozlowski J, Konarzewski M (2004). "Is West, Brown and Enquist's model of allometric scaling mathematically correct and biologically relevant?". Functional Ecology. 18 (2): 283–9. doi:10.1111/j.0269-8463.2004.00830.x
  19. ↑ Brown JH, West GB, Enquist BJ (2005). "Yes, West, Brown and Enquist's model of allometric scaling is both mathematically correct and biologically relevant". Functional Ecology. 19 (4): 735–738. doi:10.1111/j.1365-2435.2005.01022.x
  20. ↑ Brown JH, West GB, Enquist BJ (2005). "Yes, West, Brown and Enquist's model of allometric scaling is both mathematically correct and biologically relevant". Functional Ecology. 19 (4): 735–738. doi:10.1111/j.1365-2435.2005.01022.x
  21. ↑ Sieg AE, O'Connor MP, McNair JN, Grant BW, Agosta SJ, Dunham AE (November 2009). "Mammalian metabolic allometry: do intraspecific variation, phylogeny, and regression models matter?". The American Naturalist. 174 (5): 720–33. doi:10.1086/606023. PMID 19799501. S2CID 36468932
  22. ↑ Heusner, A. A. (1982-04-01). "Energy metabolism and body size I. Is the 0.75 mass exponent of Kleiber's equation a statistical artifact?". Respiration Physiology. 48 (1): 1–12. doi:10.1016/0034-5687(82)90046-9. ISSN 0034-5687. PMID 7111915
  23. ↑ Enquist BJ, West GB, Charnov EL, Brown JH (28 October 1999). "Allometric scaling of production and life-history variation in vascular plants". Nature. 401 (6756): 907–911. Bibcode:1999Natur.401..907E. doi:10.1038/44819. ISSN 1476-4687. S2CID 4397261. Corrigendum published 7 December 2000.
  24. ↑ Niklas KJ (2006). "A phyletic perspective on the allometry of plant biomass-partitioning patterns and functionally equivalent organ-categories". The New Phytologist. 171 (1): 27–40. doi:10.1111/j.1469-8137.2006.01760.x. PMID 16771980.
  25. ↑ Reich PB, Tjoelker MG, Machado JL, Oleksyn J (January 2006). "Universal scaling of respiratory metabolism, size and nitrogen in plants". Nature. 439 (7075): 457–61. Bibcode:2006Natur.439..457R. doi:10.1038/nature04282. hdl:11299/176835. PMID 16437113. S2CID 1484450 For a contrary view, see Enquist BJ, Allen AP, Brown JH, Gillooly JF, Kerkhoff AJ, Niklas KJ, Price CA, West GB (February 2007). "Biological scaling: does the exception prove the rule?". Nature. 445 (7127): E9–10, discussion E10–1. Bibcode:2007Natur.445....9E. doi:10.1038/nature05548. PMID 17268426. and associated responses.
  26. ↑ Savage VM, Allen AP, Brown JH, Gillooly JF, Herman AB, Woodruff WH, West GB (March 2007). "Scaling of number, size, and metabolic rate of cells with body size in mammals". Proceedings of the National Academy of Sciences of the United States of America. 104 (11): 4718–23. Bibcode:2007PNAS..104.4718S. doi:10.1073/pnas.0611235104. PMC 1838666. PMID 17360590.

编者推荐

集智文章推荐

令人惊叹的克莱伯法则——地球上的生物种类繁多，从生活环境到形体都千差万别，生物的物种多样性就像是大自然的馈赠，让我们生活的世界丰富多彩。在1932年，生物学家克莱伯做了一组实验，他将各种哺乳动物拉到称上称体重作为横坐标，大到几顿重的大象，小到几十克的耗子，然后通过它们在单位时间内呼出的二氧化碳，分别测量出它们的新陈代谢率作为纵坐标。得出的结果让他大吃一惊。当横纵坐标分别取对数之后，所有的动物都齐刷刷地站在了一条直线上，这条直线的斜率为3/4。生物的多样性令人叹为观止，可竟然出现了在数学上如此统一的规律。

课程推荐

克莱伯定律被誉为是生物界的“开普勒”定律，一个极为简洁漂亮的方程就出刻画了横跨30个数量级的生物体所具有的普遍规律，从新陈代谢到生老病死。我们不禁要问，这世界上真有一招打天下的普适法则么？《规模》一书会带给你答案。

文章推荐

……。1997 年，美国圣塔菲学院（Santa Fe Institute）的理论物理学家Geoffrey West及其同事在《科学》杂志上发表了一篇论文，《A General Model for the Origin of Allometric Scaling Laws in Biology》。对于那个令人捉不不透的“第四个维度”，Geoffrey West和他的同事给出了一种石破天惊的解释：新的维度来源于分形。在进化压力下，生物体倾向于使用耗能最少的方式来传递物质进行新陈代谢；因此生物体最大限度地扩大了运输资源和能量的表面积。例如我们新陈代谢的过程中，物质会通过毛细血管的表面积运向全身上下细胞，从而促进细胞生长，维持生命所需的能量。而生物体内分形结构的存在，使其有效表面积远大于其表观的物理面积。甚至产生了“升维”一样的效果……
如果人类的大小突然缩小到十分之一，会发生什么有趣的事情？

本中文词条由打豆豆参与编译，思无涯咿呀咿呀、Fernando、SyouTK编辑，欢迎在讨论页面留言。

本词条内容源自wikipedia及公开资料，遵守 CC3.0协议。

取自“https://wiki.swarma.org/index.php?title=克莱伯定律&oldid=26653”