玻尔兹曼方程

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
薄荷（讨论 | 贡献）2021年12月19日 (日) 12:55的版本 （→‎碰撞项（Stosszahlansatz）和分子混沌）
(差异) ←上一版本 | 最后版本 (差异) | 下一版本→ (差异)
跳到导航 跳到搜索


玻耳兹曼动力学方程在从微观动力学到宏观连续动力学的模型简化阶梯上的位置[1]


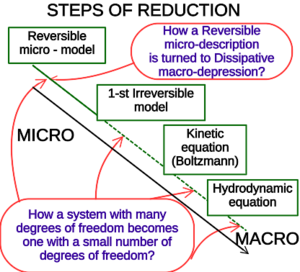
玻尔兹曼方程 Boltzmann equation或玻尔兹曼输运方程 Boltzmann transport equation（BTE）是描述非平衡状态的热力学系统统计行为的偏微分方程，由路德维希·玻尔兹曼 Ludwig Edward Boltzmann于1872年提出。[2]这类系统的经典实例是：在空间中具有温度梯度的流体，组成该流体的粒子通过随机但具有偏向性的传输使得热量从较热的区域流向较冷的区域。在现代文献中，玻尔兹曼方程一词通常用于更一般的意义上，指描述热力学系统中宏观量（如能量、电荷或粒子数变化）的任何动力学方程。


玻尔兹曼方程并不分析流体中每个粒子的位置和动量，而是考虑特定粒子的位置和动量的概率分布，此类粒子某一时刻在几何空间占据以给定位置[math]\displaystyle{ \bf{r} }[/math]为中心的小邻域（数学上的体积元[math]\displaystyle{ \mathrm{d}^3 \bf{r} }[/math]），且其动量几乎与给定动量矢量[math]\displaystyle{ \bf{p} }[/math]相等，在动量空间占据非常小的区域[math]\displaystyle{ \mathrm{d}^3 \bf{p} }[/math]。


在流体运输过程中，玻尔兹曼方程可以用来确定物理量如何变化，比如热能和动量。人们还可以推导出流体的其他特性，如粘度、热导率和电导率（通过将材料中的载流子当作气体来处理）。[2] 。


玻尔兹曼方程是非线性积分微分方程，方程中的未知函数是位置和动量在六维空间中的概率密度函数。方程解的存在唯一性仍然是未完全解决的问题，但是一些研究显示解决这一问题是很有希望的。[3][4]


概述

相空间和密度函数

系统中所有可能的位置r和动量p的集合称为系统的相空间，集合中位置坐标记为 x，y，z，动量坐标记为px，py，pz。整个空间是6维的：空间中一点可以表示为(r, p) = ( x, y, z, px, py, pz )，每个坐标由时间 t 参数化。微元（即微分体积元）写作：

[math]\displaystyle{ \text{d}^3\mathbf{r}\,\text{d}^3\mathbf{p} = \text{d}x\,\text{d}y\,\text{d}z\,\text{d}p_x\,\text{d}p_y\,\text{d}p_z. }[/math].


由于在[math]\displaystyle{ \mathrm{d}^3\bf{r} }[/math][math]\displaystyle{ \mathrm{d}^3\bf{p} }[/math]的N个分子都具有的概率都位置r和动量p存在疑问，玻尔兹曼方程的核心是f，它可以给出在某一时刻 t 单位相空间体积的概率。定义概率密度函数:f (r, p, t得到,

[math]\displaystyle{ \text{d}N = f (\mathbf{r},\mathbf{p},t)\,\text{d}^3\mathbf{r}\,\text{d}^3\mathbf{p} }[/math]

是在t时刻，关于（r，p）的微体积元[math]\displaystyle{ d^3\bf{r} }[/math]和微动量元[math]\displaystyle{ \mathrm{d}^3\bf{p} }[/math]内的分子数目，[5]在位置空间和动量空间的一个区域上积分，得出在该区域中具有位置和动量的粒子总数：

[math]\displaystyle{ \begin{align} N &=\underset{momenta}\int\text{d}^{3}\mathbf{p}\underset{positions}\int\text{d}^{3}\mathbf{r}f(\mathbf{r},\mathbf{p},t)\\[5pt] &=\underset{momenta}\iiint\; \; \; \underset{positions}\iiint f(x,y,z,p_{x},p_{y},p_{z},t)\; \text{d}x\,\text{d}y\,\text{d}z\,\text{d}p_x\,\text{d}p_y\,\text{d}p_z \end{align} }[/math]


这是一个六重积分。虽然f与一群粒子有关，但相空间是针对单一粒子进行讨论(对于所有粒子的分析通常是确定性多体系统的情况)，因为只有一个r和p是需要考虑的。使用r1, p1代表粒子1,r2, p2代表粒子2，......，直到rN, pN代表粒子N，都不在考虑范围之内。


系统假设粒子都是相同的（因此每个粒子的质量m相同）。对于组成多于一种化学物质的混合物，其中每种物质都需要一种分布。


一般形式

玻尔兹曼方程的一般形式可以写作：[6]

[math]\displaystyle{ \frac{df}{dt} = \left(\frac{\partial f}{\partial t}\right)_\text{force} + \left(\frac{\partial f}{\partial t}\right)_\text{diff} + \left(\frac{\partial f}{\partial t}\right)_\text{coll}, }[/math]

其中“force”一词指外界对粒子施加的力（而不是粒子间的作用），“diff”表示粒子扩散，“coll”表示粒子碰撞，指碰撞中粒子间相互的作用力。上述三项的具体形式将会在下文给出[6]。注意，一些作者会使用 v 表示粒子的速度，而不是动量 p，这两个物理量可以通过动量的定义p = m v联系起来。


“force”项与“diff”项

考虑一群以 [math]\displaystyle{ f }[/math] 分布的粒子。每个粒子均受到外力[math]\displaystyle{ F }[/math]的作用（不包括粒子间作用力。粒子间的作用见后面对“coll”项的处理)。


假设在时间 [math]\displaystyle{ t }[/math]，一定数量的粒子都有位置 [math]\displaystyle{ \mathbf{r} }[/math]（于微元 [math]\displaystyle{ d^3\mathbf{r} }[/math] 内），和动量 [math]\displaystyle{ \mathbf{p} }[/math]（于微元 [math]\displaystyle{ d^3\mathbf{p} }[/math] 内）。如果此时有一个力[math]\displaystyle{ \mathbf{F} }[/math]在这一瞬作用在每个颗粒上，那么在时间 [math]\displaystyle{ t + \Delta\,t }[/math]，它们的位置将会是[math]\displaystyle{ \mathbf{r} + \Delta\,\mathbf{r} = \mathbf{r} + \mathbf{p} \Delta\,t/m }[/math]，动量将变成 [math]\displaystyle{ \mathbf{p} + \Delta\,\mathbf{p} = \mathbf{p} + \mathbf{F}\Delta\,t }[/math]。在没有碰撞的情况下，[math]\displaystyle{ f }[/math]必须满足

[math]\displaystyle{ f\left ( \textbf{r}+\frac{\textbf{p}}{m}\Delta t,\textbf{p}+\textbf{F}\Delta t,t+\Delta t \right )\, d^{3}\textbf{r}\, d^{3}\textbf{p}= f(\textbf{r},\textbf{p},t)\, d^{3}\textbf{r}\, d^{3}\textbf{p} }[/math]


这里注意我们知道相空间元 [math]\displaystyle{ d^3\mathbf{r}\,d^3\mathbf{p} }[/math] 是恒定的，这一事实可以从哈密顿方程 Hamilton's Equations得知。然而，由于存在碰撞，相空间元 [math]\displaystyle{ d^3\mathbf{r}\,d^3\mathbf{p} }[/math] 中的粒子密度是可变的，所以有：

[math]\displaystyle{ \begin{align} dN_{coll} &= \left ( \frac{\partial f}{\partial t} \right )_{coll}\Delta td^{3}\textbf{r}\, d^{3}\textbf{p}\\[5pt] & = f\left ( \textbf{r}+\frac{\textbf{p}}{m}\Delta t,\textbf{p}+\textbf{F}\Delta t,t+\Delta t \right )\, d^{3}\textbf{r}\, d^{3}\textbf{p}- f(\textbf{r},\textbf{p},t)\, d^{3}\textbf{r}\, d^{3}\textbf{p}\\[5pt] & =\Delta f d^{3}\textbf{r}\, d^{3}\textbf{p} \end{align} }[/math]

 

 

 

 

(1)

其中 [math]\displaystyle{ \Delta f }[/math] 指的是[math]\displaystyle{ f }[/math]的总变化量。（1）式除以 [math]\displaystyle{ d^3\mathbf{r}\,d^3\mathbf{p}\,\Delta t }[/math] 并取极限 [math]\displaystyle{ \Delta t\,\rightarrow 0 }[/math] 和 [math]\displaystyle{ \Delta f\,\rightarrow 0 }[/math] 可得：

[math]\displaystyle{ \frac{d f}{d t} = \left(\frac{\partial f}{\partial t} \right)_\mathrm{coll} }[/math]

 

 

 

 

(2)


<math>f</math>的全微分为：

[math]\displaystyle{ \begin{align} d f & = \frac{\partial f}{\partial t} \, dt +\left(\frac{\partial f}{\partial x} \, dx +\frac{\partial f}{\partial y} \, dy +\frac{\partial f}{\partial z} \, dz \right) +\left(\frac{\partial f}{\partial p_x} \, dp_x +\frac{\partial f}{\partial p_y} \, dp_y +\frac{\partial f}{\partial p_z} \, dp_z \right)\\[5pt] & = \frac{\partial f}{\partial t}dt +\nabla f \cdot d\mathbf{r} + \frac{\partial f}{\partial \mathbf{p}}\cdot d\mathbf{p} \\[5pt] & = \frac{\partial f}{\partial t}dt +\nabla f \cdot \frac{\mathbf{p}}{m}dt + \frac{\partial f}{\partial \mathbf{p}}\cdot \mathbf{F} \, dt \end{align} }[/math]

 

 

 

 

(3)


其中 ∇ 为梯度算符，· 为点积，

[math]\displaystyle{ \frac{\partial f}{\partial \mathbf{p}} = \mathbf{\hat{e}}_x\frac{\partial f}{\partial p_x} + \mathbf{\hat{e}}_y\frac{\partial f}{\partial p_y} + \mathbf{\hat{e}}_z \frac{\partial f}{\partial p_z}= \nabla_\mathbf{p}f }[/math]

是∇的动量类比的一个简写，êx, êy, êz 为笛卡尔坐标系下的单位矢量。


最终形式

对（3）两边同除以dt 并代入（2）可得：

[math]\displaystyle{ \frac{\partial f}{\partial t} + \frac{\mathbf{p}}{m}\cdot\nabla f + \mathbf{F} \cdot \frac{\partial f}{\partial \mathbf{p}} = \left(\frac{\partial f}{\partial t} \right)_\mathrm{coll} }[/math]


这里，F(r, t) 为流体中作用在粒子上的力场，m为粒子质量。 右边的一项用于描述粒子间相互碰撞产生的影响；如果此项为零，则说明粒子之间没有碰撞。无碰撞情况下,个体碰撞被长程聚合相互作用（例如库仑相互作用）所取代，此时的玻尔兹曼方程常被称为弗拉索夫方程 Vlasov Equation。


这个方程比上一节中的一般形式更加有用，然而它依旧是不完整的：除非已知[math]\displaystyle{ f }[/math]中的碰撞项，否则[math]\displaystyle{ f }[/math]是解不出来的。这一项并不像其他项一样可以轻而易举地得到——这一项是表示粒子碰撞的统计项，需要知道粒子遵守怎样的统计规律，例如麦克斯韦-玻尔兹曼分布 Maxwell–Boltzmann Distribution，费米-狄拉克分布 Fermi–Dirac Distribution或玻色–爱因斯坦分布 Bose–Einstein Distribution。


碰撞项（Stosszahlansatz）和分子混沌

双体碰撞项

玻尔兹曼在确定碰撞项时所应用到的关键见解是：他假设的碰撞项完全是由假定在碰撞前不相关的两个粒子的相互碰撞得到的。这个假设被玻尔兹曼称为“Stosszahlansatz”，也叫做分子混沌假设 Molecular Chaos assumption。根据这一假设，碰撞项可以被写作单粒子分布函数乘积在动量空间上的积分：[2]

[math]\displaystyle{ \left(\frac{\partial f}{\partial t}\right)_\text{coll} = \iint gI(g, \Omega)[f(\mathbf{r},\mathbf{p'}_A, t) f(\mathbf{r},\mathbf{p'}_B,t) - f(\mathbf{r},\mathbf{p}_A,t) f(\mathbf{r},\mathbf{p}_B,t)] \,d\Omega \,d^3\mathbf{p}_A \,d^3\mathbf{p}_B, }[/math]

其中 [math]\displaystyle{ \mathbf{p}_A }[/math] 和 [math]\displaystyle{ \mathbf{p}_B }[/math] 表示碰撞前任意两个粒子的动量（为了方便而标记为[math]\displaystyle{ A }[/math]和[math]\displaystyle{ B }[/math]）， [math]\displaystyle{ \mathbf{p}'_A }[/math] 和 [math]\displaystyle{ \mathbf{p}'_B }[/math] 表示碰撞后的动量，

[math]\displaystyle{ g = |\mathbf{p}_B - \mathbf{p}_A| = |\mathbf{p'}_B - \mathbf{p'}_A| }[/math]


指对应动量的大小，[math]\displaystyle{ I(g, \Omega) }[/math] 是碰撞的微分散射截面 Differential Cross Section，其中碰撞粒子的相对动量通过一个角θ变为实心角dΩ的元。


对碰撞项的简化

由于求解玻尔兹曼方程时，许多挑战都来自于其复杂的碰撞项；因此人们会对碰撞项做一些建模和简化的尝试。现知最好的模型是由Bhatnagar，Gross和Krook作出的BGK近似[7]。BGK近似假设分子碰撞的影响会迫使物理空间中某一点的非平衡分布函数回到麦克斯韦平衡分布函数，且其发生率正比于分子碰撞频率。于是，玻尔兹曼方程可写作以下的BGK形式：


[math]\displaystyle{ \frac{\partial f}{\partial t} + \frac{\mathbf{p}}{m}\cdot\nabla f + \mathbf{F} \cdot \frac{\partial f}{\partial \mathbf{p}} = \nu (f_0 - f), }[/math]


其中 [math]\displaystyle{ \nu }[/math] 是分子碰撞频率，和驰豫时间 [math]\displaystyle{ \tau }[/math] 具有倒数关系：[math]\displaystyle{ \nu = 1/\tau }[/math]。[math]\displaystyle{ f_0 }[/math]是局域麦克斯韦分布函数，由空间中这一点的气体温度给定。


通用方程（对于混合物）

对于具有多种化学组分的混合物，我们以i = 1, 2, 3, ..., n标记各种成分。则对于组分i的方程是：[2]

[math]\displaystyle{ \frac{\partial f_i}{\partial t} + \frac{\mathbf{p}_i}{m_i} \cdot \nabla f_i + \mathbf{F} \cdot \frac{\partial f_i}{\partial \mathbf{p}_i} = \left(\frac{\partial f_i}{\partial t} \right)_\text{coll}, }[/math]


其中 [math]\displaystyle{ f_i = f_i(\mathbf{r}, \mathbf{p_i}, t) }[/math]。碰撞项为

[math]\displaystyle{ \left(\frac{\partial f_i}{\partial t} \right)_{\mathrm{coll}} = \sum_{j=1}^n \iint g_{ij} I_{ij}(g_{ij}, \Omega)[f'_i f'_j - f_if_j] \,d\Omega\,d^3\mathbf{p'}, }[/math]


其中 [math]\displaystyle{ f' = f'(\mathbf{p_i'}, t) }[/math]，相对动量的大小是

[math]\displaystyle{ g_{ij} = |\mathbf{p}_i - \mathbf{p}_j| = |\mathbf{p'}_i - \mathbf{p'}_j|, }[/math]


Iij是粒子i和粒子j之间的微分散射截面。此积分的和描述某一相空间元中，组分i粒子的进出。


应用与推广

守恒方程

玻尔兹曼方程可用于推导流体动力学中的质量守恒，电量守恒，动量守恒，以及能量守恒定律[8]。对于只含有一种粒子的流体，粒子数密度 [math]\displaystyle{ n }[/math] 为：

[math]\displaystyle{ n = \int f \,d^3p. }[/math]

算符A的期望值由下式给出：

[math]\displaystyle{ \langle A \rangle = \frac 1 n \int A f \,d^3p. }[/math]


由于守恒方程中包含张量，以下使用爱因斯坦求和约定 Einstein Summation Convention,乘积中的重复标记表示对这些带有标记量的求和。因此 [math]\displaystyle{ \mathbf{x}\rightarrow x_i }[/math] 且 [math]\displaystyle{ \mathbf{p}\rightarrow p_i = m w_i }[/math]，其中 [math]\displaystyle{ w_i }[/math] 为粒子速度矢量。定义某函数 [math]\displaystyle{ A(p_i) }[/math]，使得其唯一的自变量为动量 [math]\displaystyle{ p_i }[/math]（碰撞中动量守恒）。假设力 [math]\displaystyle{ F_i }[/math] 为位置的函数，且对于 [math]\displaystyle{ p_i\rightarrow\pm \infty }[/math]，[math]\displaystyle{ f }[/math] 为 0。对玻尔兹曼方程两边同乘 [math]\displaystyle{ A }[/math] ，并对动量积分，使用分部积分法可得四项。如下所示：

[math]\displaystyle{ \int A \frac{\partial f}{\partial t} \,d^3p = \frac{\partial }{\partial t} (n \langle A \rangle), }[/math]
[math]\displaystyle{ \int \frac{p_j A}{m}\frac{\partial f}{\partial x_j} \,d^3p = \frac{1}{m}\frac{\partial}{\partial x_j}(n\langle A p_j \rangle), }[/math]
[math]\displaystyle{ \int A F_j \frac{\partial f}{\partial p_j} \,d^3p = -nF_j\left\langle \frac{\partial A}{\partial p_j}\right\rangle, }[/math]
[math]\displaystyle{ \int A \left(\frac{\partial f}{\partial t}\right)_\text{coll} \,d^3p = 0, }[/math]


因为 [math]\displaystyle{ A }[/math] 在碰撞中守恒，所以最后一项为零。


令 [math]\displaystyle{ A=m }[/math]，即粒子质量，积分后的玻尔兹曼方程化为质量守恒方程[8]：

[math]\displaystyle{ \frac{\partial}{\partial t}\rho + \frac{\partial}{\partial x_j}(\rho V_j) = 0, }[/math]

[math]\displaystyle{ \rho=mn }[/math] 为质量密度，[math]\displaystyle{ V_i=\langle w_i\rangle }[/math] 为平均流体速度。


令 [math]\displaystyle{ A = p_i }[/math]，即粒子动量，积分后的玻尔兹曼方程化为动量守恒方程[8]：

[math]\displaystyle{ \frac{\partial}{\partial t}(\rho V_i) + \frac{\partial}{\partial x_j}(\rho V_i V_j+P_{ij}) - nF_i = 0, }[/math]


[math]\displaystyle{ P_{ij}=\rho\langle (w_i-V_i) (w_j-V_j) \rangle }[/math] 为压强张量（粘性应力张量加上流体静力学压强）。

令 [math]\displaystyle{ A =\frac{p_i p_i}{2m} }[/math]，即粒子动能，积分后的玻尔兹曼方程化为能量守恒方程[8]：

[math]\displaystyle{ \frac{\partial}{\partial t}(u + \tfrac{1}{2}\rho V_i V_i) + \frac{\partial}{\partial x_j} (uV_j + \tfrac{1}{2}\rho V_i V_i V_j + J_{qj} + P_{ij}V_i) - nF_iV_i = 0, }[/math]


其中[math]\displaystyle{ u=\tfrac{1}{2}\rho\langle (w_i-V_i) (w_i-V_i) \rangle }[/math] 为动力热能密度（kinetic thermal energy density），[math]\displaystyle{ J_{qi}=\tfrac{1}{2}\rho\langle (w_i-V_i)(w_k-V_k)(w_k-V_k)\rangle }[/math] 热通量矢量。


哈密顿力学

在哈密顿力学 Hamiltonian Mechanics中, 玻尔兹曼方程通常写作

[math]\displaystyle{ \hat{\mathbf{L}}[f]=\mathbf{C}[f], \, }[/math]


其中 L 是刘维尔算子 Liouville Operator(这里定义的刘维尔算子和链接文章中的定义不一致)，它描述了相空间体积的演化；C 是碰撞算子。非相对论下的L 写作

[math]\displaystyle{ \hat{\mathbf{L}}_\mathrm{NR} = \frac{\partial}{\partial t} + \frac{\mathbf{p}}{m} \cdot \nabla + \mathbf{F}\cdot\frac{\partial}{\partial \mathbf{p}}\,. }[/math]


量子理论与粒子数守恒的违背

对于碰撞中粒子数不守恒的相对论量子系统，给出相对论量子玻尔兹曼方程 Quantum Boltzmann equations是可能的。这在物理宇宙学中有一些应用[9]，包括大爆炸核合成 Big Bang Nucleosynthesis中轻元素的形成，暗物质 Dark Matter的产生和重子发生 Baryogenesis。我们并不预先知道量子系统的状态可以用经典相空间密度f 来表征。然而，对于许多应用来说，定义良好的f 作为有效玻尔兹曼方程的解是存在的，可以由量子场论的第一原理推导得出。[10]


广义相对论和天文学

玻尔兹曼方程在星系动力学中也大有可为。在一定的假设下，星系可以近似为连续流体；其质量分布可以表示为 f 。在星系中，不同星体间的物理碰撞鲜有发生。在远长于宇宙年龄的时间内，引力碰撞的影响可以被忽略。


方程在广义相对论中的推广[11]为：

[math]\displaystyle{ \hat{\mathbf{L}}_\mathrm{GR}=p^\alpha\frac{\partial}{\partial x^\alpha} - \Gamma^\alpha{}_{\beta\gamma}p^\beta p^\gamma\frac{\partial}{\partial p^\alpha}, }[/math]


其中 Γαβγ 代表第二类克里斯托费尔符号 Christoffel Symbol（这里假定没有外力，所以粒子在没有碰撞时沿着短程线运动），巧妙地传递出重要的讯息：密度是逆变-协变(xi, pi)混合相空间内的函数，而不是完全的逆变 (xi, pi)相空间[12][13]。


在物理宇宙学中，全协变方法已经应用于宇宙微波背景辐射研究[14]。 更一般地说，对早期宇宙过程的研究常常试图考虑量子力学和广义相对论的影响。[9] 大爆炸后，在非常稠密的原始等离子体介质中，粒子不断地产生和湮灭。在这样的环境中，量子相干性和波函数的空间扩展会影响动力学，使人们怀疑玻尔兹曼方程中出现的经典相空间分布f 是否适合描述这一系统。然而，在许多情况下，可以从量子场论的第一原理推导出广义分布函数的有效玻尔兹曼方程。


方程求解

在某些情况下，可以证明玻尔兹曼方程存在精确解[15]。这意味着，如果对服从玻尔兹曼方程的系统施加一个微扰，此系统最终将回到平衡状态，而不是发散到无穷，或表现出其他的行为。然而，这种存在性证明无助于我们在现实问题中求解该方程。


相反，数值方法（包括有限元 Finite Elements和格子玻尔兹曼方法 Lattice Boltzmann Methods）经常用来帮助人们寻找各种形式的玻尔兹曼方程的近似解。应用范围覆盖稀薄气流[16][17]中的高超音速空气动力学 Hypersonic Aerodynamics到等离子流[18]。电动力学中，玻尔兹曼方程可以应用于电导率的计算，其结果与半经典结果一致[19]。


在接近局部均衡的情况下，玻尔兹曼方程的解可以用克努森数幂的渐近展开来表示（查普曼-恩斯科格 Chapman-Enskog展开式[20]）。展开式的前两项给出了欧拉方程 Euler Equations和纳维-斯托克斯方程 Navier-Stokes Equations。较高阶项有奇点。从原子观点(以玻尔兹曼方程为代表)到连续体运动定律的极限过程的数学推导问题，是希尔伯特第六问题 Hilbert's Sixth Problem的重要组成部分[21]。


另见


参考文献

  1. ↑ Gorban, Alexander N.; Karlin, Ilya V. (2005). Invariant Manifolds for Physical and Chemical Kinetics. Lecture Notes in Physics (LNP, vol. 660). Berlin, Heidelberg: Springer. doi:10.1007/b98103. ISBN 978-3-540-22684-0. Alt URL
  2. ↑ 2.0 2.1 2.2 2.3 Encyclopaedia of Physics (2nd Edition), R. G. Lerner, G. L. Trigg, VHC publishers, 1991, ISBN (Verlagsgesellschaft) 3-527-26954-1, ISBN (VHC Inc.) 0-89573-752-3.
  3. ↑ DiPerna, R. J.; Lions, P.-L. (1989). "On the Cauchy problem for Boltzmann equations: global existence and weak stability". Ann. of Math. 2. 130 (2): 321–366. doi:10.2307/1971423. JSTOR 1971423.
  4. ↑ Philip T. Gressman & Robert M. Strain (2010). "Global classical solutions of the Boltzmann equation with long-range interactions". Proceedings of the National Academy of Sciences. 107 (13): 5744–5749. arXiv:1002.3639. Bibcode:2010PNAS..107.5744G. doi:10.1073/pnas.1001185107. PMC 2851887. PMID 20231489.
  5. ↑ Huang, Kerson (1987). Statistical Mechanics (Second ed.). New York: Wiley. p. 53. ISBN 978-0-471-81518-1.
  6. ↑ 6.0 6.1 McGraw Hill Encyclopaedia of Physics (2nd Edition), C. B. Parker, 1994, ISBN 0-07-051400-3.
  7. ↑ Bhatnagar, P. L.; Gross, E. P.; Krook, M. (1954-05-01). "A Model for Collision Processes in Gases. I. Small Amplitude Processes in Charged and Neutral One-Component Systems". Physical Review. 94 (3): 511–525. Bibcode:1954PhRv...94..511B. doi:10.1103/PhysRev.94.511.
  8. ↑ 8.0 8.1 8.2 8.3 de Groot, S. R.; Mazur, P. (1984). Non-Equilibrium Thermodynamics. New York: Dover Publications Inc.. ISBN 978-0-486-64741-8. 
  9. ↑ 9.0 9.1 Edward Kolb; Michael Turner (1990). The Early Universe. Westview Press. ISBN 9780201626742. 
  10. ↑ M. Drewes; C. Weniger; S. Mendizabal (8 January 2013). "The Boltzmann equation from quantum field theory". Phys. Lett. B. 718 (3): 1119–1124. arXiv:1202.1301. Bibcode:2013PhLB..718.1119D. doi:10.1016/j.physletb.2012.11.046. S2CID 119253828.
  11. ↑ Ehlers J (1971) General Relativity and Cosmology (Varenna), R K Sachs (Academic Press NY);Thorne K S (1980) Rev. Mod. Phys., 52, 299; Ellis G F R, Treciokas R, Matravers D R, (1983) Ann. Phys., 150, 487}
  12. ↑ Debbasch, Fabrice; Willem van Leeuwen (2009). "General relativistic Boltzmann equation I: Covariant treatment". Physica A. 388 (7): 1079–1104. Bibcode:2009PhyA..388.1079D. doi:10.1016/j.physa.2008.12.023.
  13. ↑ Debbasch, Fabrice; Willem van Leeuwen (2009). "General relativistic Boltzmann equation II: Manifestly covariant treatment". Physica A. 388 (9): 1818–34. Bibcode:2009PhyA..388.1818D. doi:10.1016/j.physa.2009.01.009.
  14. ↑ Maartens R, Gebbie T, Ellis GFR (1999). "Cosmic microwave background anisotropies: Nonlinear dynamics". Phys. Rev. D. 59 (8): 083506
  15. ↑ Philip T. Gressman, Robert M. Strain (2011). "Global Classical Solutions of the Boltzmann Equation without Angular Cut-off". Journal of the American Mathematical Society. 24 (3): 771. arXiv:1011.5441. doi:10.1090/S0894-0347-2011-00697-8. S2CID 115167686.
  16. ↑ Evans, Ben; Morgan, Ken; Hassan, Oubay (2011-03-01). "A discontinuous finite element solution of the Boltzmann kinetic equation in collisionless and BGK forms for macroscopic gas flows". Applied Mathematical Modelling. 35 (3): 996–1015. doi:10.1016/j.apm.2010.07.027.
  17. ↑ Evans, B.; Walton, S.P. (December 2017). "Aerodynamic optimisation of a hypersonic reentry vehicle based on solution of the Boltzmann–BGK equation and evolutionary optimisation". Applied Mathematical Modelling. 52: 215–240. doi:10.1016/j.apm.2017.07.024. ISSN 0307-904X.
  18. ↑ Pareschi, L.; Russo, G. (2000-01-01). "Numerical Solution of the Boltzmann Equation I: Spectrally Accurate Approximation of the Collision Operator". SIAM Journal on Numerical Analysis. 37 (4): 1217–1245. CiteSeerX 10.1.1.46.2853. doi:10.1137/S0036142998343300. ISSN 0036-1429.
  19. ↑ H.J.W. Müller-Kirsten, Basics of Statistical Mechanics, Chapter 13, 2nd ed., World Scientific (2013).
  20. ↑ Sydney Chapman; Thomas George Cowling The mathematical theory of non-uniform gases: an account of the kinetic theory of viscosity, thermal conduction, and diffusion in gases, Cambridge University Press, 1970. ISBN 0-521-40844-X
  21. ↑ "Theme issue 'Hilbert's sixth problem'". Philosophical Transactions of the Royal Society A. 376 (2118). 2018. doi:10.1098/rsta/376/2118.


外部链接


编者推荐

集智课程

基于神经网络的部分观测偏微分方程动力学学习

该课程室Openlab内部读书会第十七期内容，主要讨论了如何从观测到（并不完整）的数据集中学习PDEs dynamics 的问题。这篇文章提出了使用Resnet学习动力学dynamics。使用Unet 补全不完整的数据的模型。在将这两个模型耦合的方式上，作者提出了两种可行的训练模型分别是 pre-trained 和 jointly trained models，模型在EULER 和 NAVIER-STOKES EQUATIONS 达到了state-of-art 的效果。


常微分方程

本课程中，北京师范大学副教授陈六君介绍了常系数齐次线性微分方程、常系数非齐次线性微分方程、变系数线性微分方程的解法。

  • 常系数齐次线性微分方程
  • 常系数非齐次线性微分方程
  • 变系数线性微分方程


数学分析/线性代数

本课程将介绍如何用Mathematica进行微积分运算、解符号/数值微分方程。同时，还会介绍线性代数的基本工具。

  • 极限、数列
  • 微积分与微分方程
  • 线性代数
  • 图与网络：社交网络分析


其他


本中文词条由此词条由栗子CUGB翻译和审校，薄荷编辑，如有问题，欢迎在讨论页面留言。


本词条内容源自wikipedia及公开资料，遵守 CC3.0协议。

取自“https://wiki.swarma.org/index.php?title=玻尔兹曼方程&oldid=27965”