伯努瓦·曼德布洛特 Benoit Mandelbrot

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
薄荷（讨论 | 贡献）2022年1月7日 (五) 20:31的版本 （→‎编者推荐）
跳到导航 跳到搜索
See also: Mandelbrot set

基本信息

Benoit Mandelbrot, TED 2010.jpg
类别 信息
姓名 伯努瓦 曼德布洛特

[n 1] Mandelbrot

图片说明 2010年，曼德布洛特于去世前不久曾出席在TED会议上。
出生日期 1924年11月20日
出生地 波兰华沙
死亡日期 2010年10月14日
死亡地点 美国马萨诸塞州剑桥
国籍 法国，美国，波兰
主要研究方向 数学，空气动力学
母校 巴黎综合理工学院，加州理工学院，巴黎大学
博士导师 保罗·皮埃尔·莱维
博士生 L-E. 卡维，尤金·法玛，肯·穆斯格雷夫，穆拉德·塔克
著名 曼德布罗集，混沌理论，分形，Zipf –曼德尔布洛特法则
Influences 约翰内斯·开普勒，保罗·列维，索莱姆·曼德布罗特
Influenced 纳西姆·尼古拉斯·塔勒布
配偶 阿利耶特·卡甘（1955-2010）
工作机构 耶鲁大学，IBM公司，太平洋西北国家实验室
所获奖项 法国荣誉军团勋章（1990年侠士·2006年警官），2003日本国际奖，1993沃尔夫奖，1989年哈维奖，1986年富兰克林奖章，1985年巴纳德奖章


伯努瓦[n 1] 曼德布洛特[n 2]（1924年11月20日至2010年10月14日）是波兰裔法国裔美国数学家和博学家，对实用科学有着广泛的研究。[4][5][6]他热衷于研究物理现象的“粗糙艺术”和“生活中不受控制的元素”，并且将自己称为“分形主义者”，因其对分形几何学领域的贡献而受到认可，其中包括创造了“ 分形 Fractal”一词，并发展了自然界中的“ 粗糙度Roughness和 自相似性Self-similarity ”理论。[7]

1936年，当曼德布罗特还是个孩子时，一家人从波兰华沙移民到了法国。第二次世界大战结束后，曼德布洛特学习了数学，从巴黎和美国的大学毕业，并获得了加州理工学院的航空硕士学位。他的职业生涯大部分时间都是在美国和法国度过，拥有法国和美国双重国籍。1958年，他在IBM开始了35年的职业生涯，并在那里成为了IBM院士，定期请假到哈佛大学任教。在哈佛大学发表关于棉花期货的美国商品市场研究之后，他开始教授经济学和应用科学。

由于曼德布罗特可以使用IBM的计算机，他是最早使用计算机图形来创建和显示分形几何图像的人之一。他于1980年发现了曼德布洛特集合，展示了如何从简单的规则图形创建出视觉复杂的图形。他认为那些通常被认为是“粗糙”，“杂乱”或“混乱”的事物，例如云层或海岸线，实际上都具有“ 有序度 Degree of order ”[8]的性质。他以数学和几何学为中心的延申研究领域包括了统计物理学，气象学，水文学，地貌学，解剖学，分类学，神经学，语言学，信息技术，计算机图形学，经济学，地质学，医学，物理宇宙学，工程学，混沌理论等领域的贡献 ，经济物理学，冶金学和社会科学。[9]

在他职业生涯后期，他担任耶鲁大学数学科学系的斯特林教授，并且被授予了耶鲁历史上最年长的终身教授职位[10]。曼德布罗特还在西北太平洋国家实验室，里尔-北法兰西院校联盟，普林斯顿高等研究院和法国国家科学研究中心担任过职务。他的自传《分形主义者:一个科学特立独行者的回忆录The Fractalist: Memoir of a Scientific Maveric》于2012年死后出版。

早年生活

家庭背景和早期教育，（4:11）伯努瓦 曼德布洛特访谈，《Web of Stories》 144第1部分

曼德布洛特出生于波兰第二共和国时期[11] ，华沙的一个立陶宛犹太家庭。父亲以服装贸易为生，母亲是一名牙科医生。他入学后的前两年，一直由他叔叔私下辅导，这位叔叔尤其鄙视死记硬背的学习方法：“我的大部分时间都花在下棋，阅读地图和学习如何打开我的视角观察周围的一切。[12]”后来1936年，他11岁时，一家人从波兰移民到了法国。这次移民，战争，和他父亲兄弟Szolem Mandelbrojt（数学家斯佐勒姆·曼德尔贝罗亚特，1920年左右移居巴黎）的接触，更进一步阻碍了他受到规范的教育。他曾写道：“我的父母作为经济和政治难民，在法国投靠了佐勒姆，因此而挽救了我们的生命。”[13][14]

曼德布罗特在巴黎罗兰公立中学学习，一直到第二次世界大战开始，后来他的家人搬到了法国的蒂勒。后来犹太教教士大卫·菲尔韦克Rabbi David Feuerwerker（布里夫拉盖勒德犹太教教士the Rabbi of Brive-la-Gaillarde）帮助他继续学业。[13][15]当时法国大部分地区都被纳粹占领，曼德布罗特回忆起这段时期：

我们一直担心的是，一旦敌人下定决心将我们报告给当局，等待我们的就是死刑。类似的事情就发生在巴黎的一位密友Zina Morhange深上，她曾是附近某个县城的医生。当时只是为了解决竞争对手，另一位医生就举报了她...而我们逃过了一劫。谁知道是为什么？

1944年，曼德布洛特回到巴黎，在里昂的帕克中学学习，并于1945年至1947年考上了巴黎综合理工学院，在加斯顿·朱莉亚Gaston Julia和保罗·列维Paul Lévy的指导下学习。之后的1947年到1949年，他就读于加利福尼亚理工学院，在那里获得了航空硕士学位[2] 返回法国后，他于1952年在巴黎大学获得数学科学博士学位。[12]

科研生涯

自1949年到1958年，曼德布洛特任职于法国国家科学研究中心。在此期间，他得到了约翰·冯·诺伊曼John von Neumann的赞助，在新泽西州普林斯顿的高级研究学院度过了一年。1955年，他与阿利耶特·卡甘结婚，并搬到瑞士日内瓦（与国际遗传认识论中心的让·皮亚杰Jean Piaget合作），后来又迁往法国里尔大学[16] 。到了1958年，这对夫妇搬到了美国，在那里曼德布洛特加入了位于纽约约克敦高地的IBM托马斯·沃森研究中心[16]。他在IBM待了35年，并且成为IBM院士，后来成为了荣誉退休院士。[12] 从1951年起，曼德布洛特开始致力于研究相关问题并发表论文，不仅在数学领域，而且在信息论，经济学和流体动力学等应用领域中也发表许多研究论文。

金融市场的随机性

曼德布洛特将金融市场视为“野生随机性”的很好案例，其特征是集中性和长相关性。为此他开发了几种可以模拟财务波动的创新方法[17] 。在他的早期工作中，他发现金融市场的价格变化并非遵循高斯分布，而是遵循具有无限方差的 列维稳定分布 Lévy stable distributions 。他发现，例如棉花价格遵循列维稳定分布，其参数α等于1.7，而不是高斯分布中的2。该“稳定”分布具有以下性质：随机变量的许多实例总和遵循相同的分布，只是比例参数较大。[18]

“分形几何”和曼德布洛特集合的发展

作为哈佛大学的客座教授，曼德布洛特开始研究名为朱莉娅集合Julia Sets的分形，这些分形在复杂平面的变换下依旧保持不变。在加斯顿·朱莉娅 Gaston Julia和皮埃尔·法图Pierre Fatou先前工作的基础上，曼德尔布洛特使用计算机绘制出了朱莉娅集合的图像。在他研究这些朱莉娅集的拓扑时，他于1979年提出的曼德布洛特集。1982年，他在《大自然的分形几何学The Fractal Geometry of Nature》[19] 一书中扩展并更新了他的思想。但是这项颇具影响力的著作不仅将分形技术引入到专业数学和大众数学中，也同时进入到了那些将分形技术仅视为“程序工件”的批评者眼中。

曼德布洛特在2006年法国荣誉军团勋章的提名演讲，当时他提到了曼德布洛特集合

1975年，曼德布洛特创造了“分形”一词来描述这些结构，并首先发表了他的想法，其翻译为《分形：形式，机会和维度Fractals: Form, Chance and Dimension》[20] 。根据计算机科学家和物理学家斯蒂芬·沃尔夫拉姆Stephen Wolfram的说法，这本书对曼德尔布洛特来说是一个“突破”，他在那之前通常会“将相当简单的数学应用于……以前几乎没有看到过的严肃数学领域”[8]。沃尔夫拉姆补充说，由于这项新研究，他不再是“流浪的科学家”，他被称为“分形之父”：

事实证明曼德布洛特最终完成了一部伟大的科学著作。他建立了一个基本的概念，简单地说，有些几何形状（他称之为“分形”）在各个尺度上都同样“粗糙”。不管您凑多近去看，它们都永远不会变得简单，就像您在脚下看到的多岩石的海岸线与从太空中看到的伸展部分一样参差不齐。

沃尔夫拉姆简要地将分形描述为几何重复的一种形式，“在其中，越来越少的相同复制图案相继被嵌套在彼此内部，因此无论您放大多少，同样的复杂形状都会展现出来。蕨叶和罗马式西兰花是自然界的两个例子。“[8]他指出了一个出乎意料的结论： 可能有人以为，这种简单而基本的规律已经被研究了数百年甚至数千年，但事实并非如此。实际上，它仅在过去30多年中才受到关注，而且几乎完全是通过一个人的努力，即数学家伯努瓦 曼德布洛特。

曼德布洛特使用“分形”一词，因为它源自拉丁语 fractus”，意为碎玻璃。通过使用新开发的IBM计算机和图形计算机代码，曼德布洛特创建了分形图像，这些图像被采访者描述为“1960年代迷幻艺术的疯狂，其形式令人不禁联想到自然和人体”。他还将自己视为“未来的开普勒”（在17世纪，科学家约翰尼斯·开普勒Johannes Kepler计算并描述了行星的轨道）。[21]

一个德布洛特集合

但是，曼德布洛特从未觉得他在发明一个新概念。在他与科学作家亚瑟·克拉克Arthur C. Clarke的纪录片中他描述了自己的感受：

在探索这个集合的时候我并未感觉在发明一个新概念。我也从没有感觉到我的想象力足以发现所有这些非凡的事物。其实他们就一直呈现在那里，只是过去没有人注意过他们。一个如此简单的公式就可以解释所有这些异常复杂的事物，太难以置信了。因此，科学的目标是从一团乱开始，再由一个简单的公式来解释它。我想这是研究科学的梦想。[22]

克拉克Clarke说：“曼德布洛特集确实是整个数学史上最惊人的发现之一。谁能想到，如此难以置信的简单方程式就可以生成视觉上无限复杂的图像？“克拉克还注意到了一个奇怪的巧合”：我确信曼德布洛特的名称和“曼陀罗”（一个宗教象征）一词纯属巧合，但确实曼德布洛特集似乎包含了大量的曼陀罗。[22] 经过35年零12天的努力，曼德布洛特在1987年离开了IBM，当时IBM决定结束其部门的研究[23] 。随后他加入了耶鲁大学数学系，并于1999年以75岁的高龄获得了第一任终身职位.[24]。在2005年退休之时，他成为了斯特林数学科学教授。

分形与“粗糙度理论”

曼德布洛特创造了第一个“粗糙度理论”，他看到了山脉，海岸线和河流盆地形状的“粗糙度”。植物，血管和肺的结构的“粗糙度”；还有星系聚集的“粗糙度”。他个人的追求是创建一些数学公式来测量此类物体在自然界中的整体“粗糙度”[13]。他首先问自己各种与自然有关的问题：

几何图形能否传达其希腊词根[geo-]所蕴含的内容，即追求真实的测量数据？[13]不仅能测量尼罗河沿岸的耕地，还能测量未开发的土地？[13]

曼德布洛特在1967年《科学》杂志上发表的论文《英国的海岸线有多长？统计自相似性和分形维数How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension》中讨论了 豪斯多夫维数 Hausdorff dimension的自相似曲线。这些都是分形的例子，尽管当时曼德布洛特在论文中并没有使用这个术语，因为他直到1975年才创造这个名词。该论文是曼德布洛特关于分形主题的第一批出版物之一。[25]

[26]

曼德布洛特特地强调可以使用分形作为描述现实世界中多数“粗糙”现象的模型，因其能真实且有效地展现出来。他还总结道：“实际粗糙度通常都是分形的，是可以测量出来的。” [13]不过，尽管他创造了“分形”一词，但他在《大自然的分形几何学》中提出的一些数学现象之前曾被其他数学家描述过。只是在曼德布洛特之前，这些现象被视为不自然并且非直觉特性的特例存在。是曼德布洛特首次将这些现象或物体放在一起，并将它们变成了必要的工具，通过长期的努力，以科学的范畴去解释现实世界中这些非光滑的“粗糙”物体。

“我越来越喜欢的几何形式是最古老，最具体，最包容的几何形式，特别是由眼睛，由手，甚至由当今计算机提供协助去赋予其力量……为认识和感知世界带来统一的元素……并且，在不经意间，作为创造美的目的，其实这也相当于是额外奖赏。”

分形也同样存在于人类的追求中，例如音乐，绘画，建筑和股票市场价格。曼德布洛特认为，分形超脱于自然，而且在许多方面比传统欧几里得几何形状的人工光滑物体更直观，更自然：

Clouds are not spheres, mountains are not cones, coastlines are not circles, and bark is not smooth, nor does lightning travel in a straight line. 云不是球形，山不是圆锥形，海岸线不是圆形，树皮不是光滑的，闪电也不是直线传播的。
-来自于曼德布洛特的《大自然的分形几何学》介绍

曼德布洛特集合的部分

曼德布洛特被称为艺术家，他是一位有远见[27] 和特立独行的人[28] 。他非正式和热情的写作风格以及对视觉和几何直觉的重视（并辅以大量插图的支持）使非专业人士可以亲身体会《大自然的分形几何学》。这本书引起了大众对分形的广泛兴趣，并为混沌理论以及科学和数学的其他领域做出了贡献。

曼德布洛特也将他的想法运用到了宇宙学中。他在1974年对 奥伯斯佯谬 Olbers' paradox （“夜空之谜”）提出了新的解释，证明了分形理论的结果是解决悖论的充分非必要条件。他推测，如果宇宙中的恒星是分形分布的（例如像 康托尔尘埃 Cantor dust一样），则不必依靠大爆炸理论来解释这一悖论。他的模型不能排除“大爆炸”的发生，但是即使没有发生“大爆炸”，也可以允许黑暗的天空。[29]

奖项与荣誉

曼德布洛特获得了诸多奖项，包括1993年的沃尔夫物理学奖，2000年的欧洲地球物理学会的Lewis Fry Richardson奖，2003年的日本国际奖[30]以及2006年的美国数学学会的爱因斯坦讲师称号。

后来以他的名字命名了小行星27500 曼德布洛特。1990年11月，他被授予法国荣誉军团勋章。2005年12月，他被任命为太平洋西北国家实验室的巴特尔研究所研究员[31] 。于2006年1月晋升为荣誉军团军官[32] 。在2010年5月，约翰·霍普金斯大学的毕业典礼上授予曼德布洛特荣誉学位。[33]

曼德布洛特获得的部分奖励清单[34]:

  • 2004 Best Business Book of the Year Award
  • AMS Einstein Lectureship
  • Barnard Medal
  • Caltech Service
  • Casimir Funk Natural Sciences Award
  • Charles Proteus Steinmetz Medal
  • High School Spelling Bee (1940)
  • Fellow, American Geophysical Union
  • Fellow of the American Statistical Association[35]
  • Fellow of the American Physical Society (1987) [36]
  • Franklin Medal
  • Harvey Prize (1989)
  • Honda Prize
  • Humboldt Preis
  • IBM Fellowship
  • Japan Prize (2003)
  • John Scott Award
  • Légion d'honneur (Legion of Honour)
  • Lewis Fry Richardson Medal
  • Medaglia della Presidenza della Repubblica Italiana
  • Médaille de Vermeil de la Ville de Paris
  • Nevada Prize
  • Member of the Norwegian Academy of Science and Letters.[37]
  • Science for Art
  • Sven Berggren-Priset
  • Władysław Orlicz Prize
  • Wolf Foundation Prize for Physics (1993)

死亡与遗产

曼德布洛特于2010年10月14日在马萨诸塞州剑桥市的一家救济院死于胰腺癌，享年85岁。数学家海因茨·奥托·皮特根Heinz-Otto。[1][38] Peitgen听闻他去世的消息后说道：“如果我们谈论数学领域的影响以及在科学界的应用，曼德布洛特毫无疑问是过去五十年来最重要的人物之一。”[1]

TED会议策展人克里斯·安德森Chris Anderson将曼德布洛特描述为“改变我们看待世界的标志性人物”。[39]曼德布洛特逝世时法国总统尼古拉斯·萨科齐Nicolas Sarkozy表示，曼德布洛特具有“大胆创新的思想，从不回避改革并打破先入为主的观念……他的工作完全是在主流研究之外发展，从而催生了现代信息论。”[40] 在《经济学人》上发表的曼德布洛特讣告指出，他是“超越学院之外的名家”，并称赞他是“分形几何之父”。[41]

畅销的散文作家纳西姆·尼古拉斯·塔勒布 Nassim Nicholas Taleb表示，曼德布洛特的《市场行为The（Mis）Behavior of Markets》在他看来是“有史以来最深，最现实的金融书”。[7]

参考书目

  • 分形：形式，机会和维度 Fractals: Form, Chance and Dimension, 1977, 2020
  • 大自然的分形几何学 The Fractal Geometry of Nature, 1982
  • 金融分形和规模化：间断性，集中性，风险。Fractals and Scaling in Finance: Discontinuity, Concentration, Risk. Selecta Volume E, 1997 by Benoit B. Mandelbrot and R.E. Gomory
  • 分形，机会和财务 Fractales, hasard et finance, 1959-1997, 1 November 1998
  • 多重分形和1 /ƒ噪声：物理学中的自仿射性 (1963–1976) Multifractals and 1/ƒ Noise: Wild Self-Affinity in Physics (1963–1976) (Selecta; V.N) 18 January 1999 by J.M. Berger and Benoit B. Mandelbrot
  • 高斯自仿射性和分形：全局性，地球，1 / f噪声和R / S Gaussian Self-Affinity and Fractals: Globality, The Earth, 1/f Noise, and R/S (Selected Works of Benoit B. Mandelbrot) 14 December 2001 by Benoit Mandelbrot and F.J. Damerau
  • 分形与混沌：曼德布洛特集及其他 Fractals and Chaos: The Mandelbrot Set and Beyond, 9 January 2004
  • 市场的不当行为：金融动荡的分形观点 The Misbehavior of Markets: A Fractal View of Financial Turbulence, 2006 by Benoit Mandelbrot and Richard L. Hudson
  • 分形主义者:一个科学特立独行者的回忆录 The Fractalist: Memoir of a Scientific Maverick, 2014
  • 分形，机会和财务, 1959-1997, 1 November 1998

流行文化参考

  • 1992年，作家皮尔斯·安东尼Piers Anthony撰写了《分形模式》，其中通过分形将多个宇宙联系在一起的想法是故事中世界建构的重点。
  • 2004年，美国歌手兼作词人乔纳森·库尔顿Jonathan Coulton创作了《曼德布洛特集》。其歌词包含“曼德布洛特在天堂/至少是他死后的去向/现在他还活着并在耶鲁教数学”这句话。曼德布洛特在2010年过世后，该歌曲的现场表演仅以第一句歌词和简短的摇滚乐器来呈现。
  • 2007年，作者劳拉·鲁比Laura Ruby出版了《混沌之王》，其中包括一个名叫曼德尔布洛特的角色以及对混沌理论的讨论。
  • 2017年，扎克·韦纳史密斯Zach Weinersmith的网络漫画《星期六的谷物早餐》描绘了曼德布洛特。[42]
  • 2017年，莉兹·齐姆斯卡Liz Ziemska出版了中篇小说《曼德尔布洛特的壮丽》（Mandelbrot The Magnificent），对曼德布洛特在第二次世界大战期间如何拯救家人进行了虚构描述。

其他参考资料

  • 1 / f噪声 1/f noise –幅度与频率成反比的信号类型
  • 分形维数 Fractal dimension –一个比率，表示复杂度随比例变化的统计指标
  • 分数布朗运动 Fractional Brownian motion
  • 英国海岸线有多长？– 伯努瓦 曼德布洛特的论文讨论了分形的性质（但内容未使用该术语）
  • 赫斯特指数 Hurst exponent – 衡量时间序列的长期依赖性
  • 峰度风险 Kurtosis risk – 决策理论术语
  • 间隙度 Lacunarity – 几何和分形分析术语
  • 劳伦斯·巴施里耶 Louis Bachelier – 法国数学经济学先驱
  • 曼德布洛特竞赛–高中数学竞赛
  • 多重分形系统 Multifractal system – 具有多重分形维数的系统
  • 自相似性 Self-similarity – 对象的整体在数学上与其自身相似
  • 七种随机状态 Seven states of randomness – 随机性思想的概括
  • 偏度风险 Skewness risk – 财务建模术语
  • Zipf–曼德布洛特定律–离散概率分布

注释

  1. ↑ 1.0 1.1 In his autobiography, Mandelbrot did not add a circumflex to the "i" (i.e. "î") in his first name, as is usual for the French given name. He included "B" as a middle initial. His New York Times obituary stated that "he added the middle initial himself, though it does not stand for a middle name",[1] an assertion that is supported by his obituary in The Guardian.[2]
  2. ↑ Pronounced in English.When speaking in French, Mandelbrot pronounced his name.[3]

参考文献

分类: 法国科学家

  1. ↑ 1.0 1.1 1.2 Hoffman, Jascha (16 October 2010). "Benoît Mandelbrot, Mathematician, Dies at 85". The New York Times. Archived from the original on 18 October 2010. Retrieved 16 October 2010.
  2. ↑ 2.0 2.1 Lesmoir-Gordon, Nigel (17 October 2010). "Benoît Mandelbrot obituary". The Guardian. London. Archived from the original on 17 September 2013. Retrieved 17 October 2010.
  3. ↑ Recording of the ceremony on 11 September 2006 at which Mandelbrot received the insignia for an Officer of the Legion of Honour|Légion d'honneur.
  4. ↑ "Archived copy". Archived from the original on 8 January 2018. Retrieved 8 January 2018.{{cite web}}: CS1 maint: archived copy as title (link)
  5. ↑ Benoit Mandelbrot: Fractals and the art of roughness， ted.com (February 2010)
  6. ↑ Hudson & Mandelbrot, Prelude, page xviii
  7. ↑ 7.0 7.1 Gomory, R. (2010). "Benoît Mandelbrot (1924–2010)". Nature. 468 (7322): 378. Bibcode:2010Natur.468..378G. doi:10.1038/468378a. PMID 21085164.
  8. ↑ 8.0 8.1 8.2 Wolfram, Stephen. "The Father of Fractals" Wall Street Journal, 22 November 2012
  9. ↑ list includes specific sciences mentioned in Hudson & Mandelbrot, the Prelude, p. xvi, and p. 26
  10. ↑ "The Genius of the Unpredictable". Yale Alumni Magazine. November–December 2004. Archived from the original on 22 October 2014. Retrieved 22 July 2014.
  11. ↑ Hoffman, Jascha (2010-10-16). "Benoît Mandelbrot, Novel Mathematician, Dies at 85 (Published 2010)". The New York Times (in English). ISSN 0362-4331. Archived from the original on 21 January 2017. Retrieved 2020-11-20.
  12. ↑ 12.0 12.1 12.2 Mandelbrot, Benoît (2002). "The Wolf Prizes for Physics, A Maverick's Apprenticeship" (PDF). Imperial College Press. Archived (PDF) from the original on 3 December 2013. Retrieved 23 April 2012.
  13. ↑ 13.0 13.1 13.2 13.3 13.4 13.5 Mandelbrot, Benoit (2012). The Fractalist: Memoir of a Scientific Maverick, Pantheon Books.
  14. ↑ "BBC News – 'Fractal' mathematician Benoît Mandelbrot dies aged 85". BBC Online. 17 October 2010. Archived from the original on 18 October 2010. Retrieved 17 October 2010.
  15. ↑ Hemenway P. (2005) Divine proportion: Phi in art, nature and science. Psychology Press.
  16. ↑ 16.0 16.1 Barcellos, Anthony (1984). "Mathematical People, Interview of B. B. Mandelbrot" (PDF). Birkhaüser. Archived (PDF) from the original on 27 April 2015. Retrieved 25 June 2013.
  17. ↑ "Mandelbrot, Benoit". Wiley. 19 April 2010. ISBN 9780470057568. 
  18. ↑ "New Scientist, 19 April 1997". Newscientist.com. 19 April 1997. Archived from the original on 21 April 2010. Retrieved 17 October 2010.
  19. ↑ The Fractal Geometry of Nature by Benoît Mandelbrot; W H Freeman & Co, 1982;
  20. ↑ Fractals: Form, Chance and Dimension, by Benoît Mandelbrot; W H Freeman and Co, 1977;
  21. ↑ Ivry, Benjamin. "Benoit Mandelbrot Influenced Art and Mathematics"Forward, 17 November 2012
  22. ↑ 22.0 22.1 "Arthur C Clarke – Fractals – The Colors Of Infinity", video interviews, 54 min.
  23. ↑ Mandelbrot, Benoît; Bernard Sapoval; Daniel Zajdenweber (May 1998). "Web of Stories • Benoît Mandelbrot • IBM: background and policies". Web of Stories. Archived from the original on 8 September 2011. Retrieved 17 October 2010.
  24. ↑ Tenner, Edward (16 October 2010). "Benoît Mandelbrot the Maverick, 1924–2010". The Atlantic. Archived from the original on 18 October 2010. Retrieved 16 October 2010.
  25. ↑ "Dr. Mandelbrot traced his work on fractals to a question he first encountered as a young researcher: how long is the coast of Britain?": Benoit Mandelbrot (1967). "Benoît Mandelbrot, Novel Mathematician, Dies at 85 ", The New York Times.
  26. ↑ Mandelbrot, Benoit B. (5 May 1967). "How long is the coast of Britain? Statistical self-similarity and fractional dimension" (PDF). Science. 156 (3775): 636–638. Bibcode:1967Sci...156..636M. doi:10.1126/science.156.3775.636. PMID 17837158. Archived from the original on 13 July 2015. Retrieved 11 January 2016.
  27. ↑ ""Mandelbrot's Vision for Mathematics" in Proceedings of Symposia in Pure Mathematics. Volume 72.1" (PDF). American Mathematical Society. 2004. Archived from the original (PDF) on 9 December 2006. Retrieved 5 January 2007.
  28. ↑ Jersey, Bill (24 April 2005). "A Radical Mind". Hunting the Hidden Dimension. NOVA/ PBS. Archived from the original on 22 August 2009. Retrieved 20 August 2009.
  29. ↑ Galaxy Map Hints at Fractal Universe, by Amanda Gefter; New Scientist; 25 June 2008
  30. ↑ Laureates of the Japan Prizejapanprize.jp
  31. ↑ "PNNL press release: Mandelbrot joins Pacific Northwest National Laboratory". Pnl.gov. 16 February 2006. Archived from the original on 12 January 2009. Retrieved 17 October 2010.
  32. ↑ "Légion d'honneur announcement of promotion of Mandelbrot to officier" (in français). Legifrance.gouv.fr. Archived from the original on 20 November 2020. Retrieved 17 October 2010.
  33. ↑ "Six granted honorary degrees, Society of Scholars inductees recognized". Gazette.jhu.edu. 7 June 2010. Archived from the original on 17 June 2010. Retrieved 17 October 2010.
  34. ↑ Mandelbrot, Benoit B. (2 February 2006). "Vita and Awards (Word document)". Retrieved 6 January 2007. Retrieved from Internet Archive 15 December 2013.
  35. ↑ View/Search Fellows of the ASA accessed 20 August 2016.
  36. ↑ "APS Fellow Archive". APS. Archived from the original on 20 November 2020. Retrieved 24 September 2020.
  37. ↑ "Gruppe 1: Matematiske fag" (in norsk). Norwegian Academy of Science and Letters. Archived from the original on 10 November 2013. Retrieved 7 October 2010.
  38. ↑ "Benoît Mandelbrot, fractals pioneer, dies". United Press International. 16 October 2010. Archived from the original on 25 June 2013. Retrieved 17 October 2010.
  39. ↑ "Mandelbrot, father of fractal geometry, dies". Archived from the original on 19 October 2010. Retrieved 16 October 2010.
  40. ↑ "Sarkozy rend hommage à Mandelbrot" [Sarkozy pays homage to Mandelbrot]. Le Figaro (in français). Archived from the original on 25 June 2013. Retrieved 17 October 2010.
  41. ↑ Benoît Mandelbrot's obituary . The Economist (21 October 2010)
  42. ↑ "Saturday Morning Breakfast Cereal – Mandelbrot". Archived from the original on 7 October 2017. Retrieved 6 October 2017.

参考书目

  • Hudson, Richard L.; Mandelbrot, Benoît B. (2004). 市场的（错误）行为：风险，破产和回报的分形观点 New York: Basic Books. ISBN 978-0-465-04355-2.

拓展阅读

  • Mandelbrot, Benoit B. (2010). 分形论者，科学特立独行者的回忆录 New York: Vintage Books, Division of Random House.
  • Mandelbrot, Benoît B. (1983). 大自然的分形几何学. San Francisco: W.H. Freeman. ISBN 978-0-7167-1186-5. 
  • Heinz-Otto Peitgen, Hartmut Jürgens, Dietmar Saupe and Cornelia Zahlten: 分形：一个生动的讨论 (63 min video film, interviews with Benoît Mandelbrot and Edward Lorenz, computer animations), W.H. Freeman and Company, 1990. (re-published by Films for the Humanities & Sciences,
  • Mandelbrot, Benoit B. (1997) 金融分形和规模化：间断性，集中性，风险, Springer.
  • Mandelbrot, Benoît (February 1999). "华尔街的多重分形步伐". Scientific American. 280 (2): 70. Bibcode:1999SciAm.280b..70M. doi:10.1038/scientificamerican0299-70.
  • Mandelbrot, Benoit B., 高斯自仿射性和分形, Springer: 2002.
  • Mandelbrot, Benoît; Taleb, Nassim (23 March 2006). "关注证明规则的例外情况". Financial Times. Archived from the original on 23 October 2010. Retrieved 17 October 2010.
  • Frame, Michael; Cohen, Nathan (2015). 伯努瓦 曼德布洛特：多维度的生活. Singapore: World Scientific Publishing Company. ISBN 978-981-4366-06-9. 
  • Mandelbrot, B. (1959) 帕累托列维随机过程，变量和收入分配（法文） Comptes rendus de l'Académie des Sciences de Paris, 249, 613–615.
  • Mandelbrot, B. (1960) 帕累托列维随机过程，变量和收入分配（英文） International Economic Review, 1, 79–106.
  • Mandelbrot, B. (1961) 稳定的帕累托随机函数和收入的倍增变化. Econometrica, 29, 517–543.
  • Mandelbrot, B. (1964) 随机游走，火灾造成的损失和其他帕累托风险现象. Operations Research, 12, 582–585.

相关链接

  • 伯努瓦 曼德布洛特，来自于数学系谱项目
  • 曼德布洛特，来自于耶鲁大学网站
  • "伯努瓦 曼德布洛特：分形和粗糙的艺术"，来自TED演讲
  • 科学，工程和金融的分形 (公开课).
  • FT.com进行了有关金融市场主题的采访，其中包括曼德布洛特对“有效市场”假设的批评。
  • Taylor, Richard (2011). "讣告：伯努瓦 曼德布洛特". Physics Today. 64 (6): 63. Bibcode:2011PhT....64f..63T. doi:10.1063/1.3603925.
  • 曼德布洛特和他的人生故事 (网站Web of Stories).
  • 尤金·丁金Eugene Dynkin的数学访谈集锦 (1 January 1981, Ithaca, NY), 康奈尔大学图书馆
  • 曼德布洛特集的视频动画, zoom factor 10342.
  • 曼德布洛特在YouTube上的视频动画，展现了3D版的曼德布洛特集。
  • 在YouTube上飞越动画曼德布洛特世界的视频
  • 伯努瓦 曼德布洛特，来自于IMDb
  • 伯努瓦 曼德布洛特，来自于TED演讲

编者推荐

集智课程

Fractals

本课程中，以 Koch Curve 和 Box Counting 为例，讲解分形与分形维数。


分形的世界

本课程中，主要介绍了分形现象、分形维数、利用分形规律的计算方法以及混沌。


集智文章传递

分形是描述复杂几何形体结构的一种数学概念。它一般指维数取非整数的几何形体。在数学中，分形是欧几里德空间 Euclidean Space的一个子集，其分形维数的数值远远大于切赫-勒贝格维数 Topological Dimension（也称覆盖维数）。维数一般是指确定整个图形中点的位置所需要的坐标（或参数）的个数。 分形在不同的尺度上看起来是相似的，就像曼德布洛特集 Mandelbrot set的连续放大一样，因此，分形在自然界中无处不在。

每个三角形一分为四，依次迭代，形成逼真山脉

分形几何学，就是一门以不规则形态为研究对象的几何学。分形最大的特性是具有自相似性，不管是放大或者缩小研究对象，你都会看到局部和整体具有相似的结构。因为分形几何的研究对象普遍存在于大自然中，例如我们熟知的雪花、树叶、群山、云朵、海浪等等，所以分形几何学，又被称为是“大自然的几何学”。

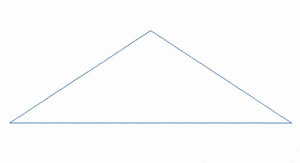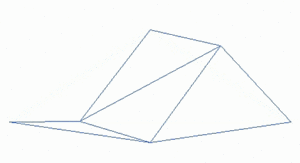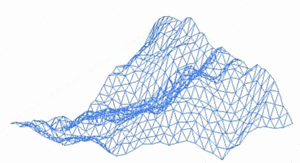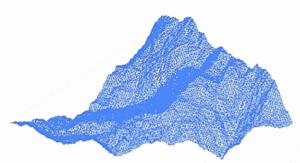
但同时分形在现实生活中有广泛的应用，包括在动画制作，3D建模、疾病监测、股票市场以及通信等领域。分形第一次应用的电影是《星际迷航2-可汗之怒》，计算机科学家Loren Carpenter从一个全景图出发， 由一些非常粗略的三角形构成，然后对于每个三角形，分成4个小三角形，继续这样操作下去，迭代，形成了非常逼真的山脉。


其他


本中文词条由Jie参与编译，AvecSally审校，糖糖、薄荷编辑，如有问题，欢迎在讨论页面留言。

本词条内容源自wikipedia及公开资料，遵守 CC3.0协议。

取自“https://wiki.swarma.org/index.php?title=伯努瓦·曼德布洛特_Benoit_Mandelbrot&oldid=28349”