多稳态
在动力系统中,多稳态是系统中的一种状态属性,即由该系统的状态所形成的向量空间中,存在多个稳定平衡点。根据数学上的必然性,在稳定点之间也一定存在不稳定的平衡点。
与L1、L2、L3前拉格朗日点一样,在某些维度上稳定而在其他维度上不稳定的点被称为不稳定点。
双稳态
双稳态是具有两个稳定平衡点的特殊情形。这是多重稳定性的最简单形式,可以发生在只有一个状态变量的系统中,因为它只需要一个一维空间来分隔两个点。[1]
在势能方面,一个双稳态系统有两个局部势能极小值,它们之间有一个局部极大值。一个双稳态的机械设备的例子是灯的开关,开关要么“开”要么“关”,但不会在二者之间停留。 在保守力场中,双稳态基于势能有三个平衡点的事实,其中两个极小,一个极大。通过数学讨论可知,极大值一定在两个极小值之间。一个处于基态的粒子位于两个平衡点中的一个,因为这对应着能量最小值。最大值可以被看作它们之间的一道屏障。
如果一个系统获得足够的活化能来穿过屏障(在化学例子中对比活化能与阿伦尼乌斯公式),那么它就可以从一个能量最小态过渡到另一个能量最小态。达到界限后,系统会在松弛时间后进入另一个能量最小态。
双稳态在数字电子设备中被广泛用于存储二进制数据。一个双稳态设备以一种状态代表“0”,另一种状态代表“1”的形式储存1比特的二进制数据。它同样被应用于张弛振荡器、多谐振荡器及施密特触发器。视觉双稳态是一些特定的视觉设备的分布,根据输入,这些设备中有两个稳定的共振的传送状态。双稳态也可以出现在生物化学系统中,它从持续的化学浓度和化学反应中产生数字式、开关式的输出。在这些系统中双稳态通常与滞后现象有关。
数学建模
在动态系统分析的数学语言中,最简单的双稳态系统之一是: [math]\displaystyle{ \frac{dy}{dt}=y\left(1-y^2\right) }[/math]
这个系统描述了一个沿着曲线[math]\displaystyle{ \frac{y^4}{4}-\frac{y^2}{2} }[/math]下滑的球,有三个定态:[math]\displaystyle{ y=1 }[/math],[math]\displaystyle{ y=0 }[/math],[math]\displaystyle{ y=-1 }[/math]和中间的定态是不稳定的,其它两个是稳定的。[math]\displaystyle{ y(t) }[/math]随时间变化的方向取决于初始条件[math]\displaystyle{ y(0) }[/math]。如果初始条件是正的,那么解y(t)随时间变化趋于1;但如果初始条件是负的,那么解[math]\displaystyle{ y(t) }[/math]随时间变化趋于-1。因此,这个动力系统是“双稳态”的。根据初值的不同,终态即可能是[math]\displaystyle{ y=1 }[/math]也可能是[math]\displaystyle{ y=-1 }[/math]。
可以通过[math]\displaystyle{ 系统=y(r-y) }[/math]来理解双稳态区域的表型,这个系统经历了一个分岔系数是[math]\displaystyle{ r }[/math]的超临界叉式分岔。
初始不稳定性
在不稳定平衡点附近,任何系统对噪声、初始条件和系统参数都很敏感,这肯能会导致它向多个不同的方向发展。
在经济学和社会科学中,路径依赖导致了发展方向上的分歧。一些路径的依赖过程可以通过多稳态来充分描述:在到达稳态之前,对输入的初始状态很敏感,比如最初市场份额不稳定,随后可能会演变成多个可能的供应商之一的稳定垄断。
多稳态知觉
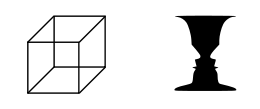
多稳态知觉是一种较少见的视知觉现象。多稳态知觉常被描述为在观看一图形时,会主观性的观察到图形无法预期的自发性改变,并且这改变会接续不断发生。
当一个图形对人类的视觉系统来说,是具有歧义性时,就会引发多稳态知觉的现象。如一些知名的例子如奈克方块Necker cube、运动中探知结构(structure from motion)、单眼竞争(monocular rivalry)和双眼竞争binocular rivalry。但更为人所知的是暧昧图形(ambiguous image)。因为这些图形通常会在两种知觉状态之间相互交换,所以又称为双稳态知觉。通过横向抑制,其中一个图像在受到刺激时会抑制邻近图像的活动。[2]
外部链接
参考文献
- ↑ https://baike.baidu.com/item/%E5%8F%8C%E7%A8%B3%E6%80%81
- ↑ Eagleman, David (2001). "Visual Illusions and Neurobiology" (PDF). Nature Reviews Neuroscience. 2 (12): 920–926. doi:10.1038/35104092. Archived from the original (PDF) on 2007-09-27.
{{cite journal}}: Unknown parameter|deadurl=ignored (help)
编者推荐
动力系统稳定性初步
对于现实的动力系统,并不是动力系统所有的解都能够被轻易观测到。有些解存在但几乎不会被观测到,只有具有某种稳定性的结构和结果才能被观测到。所以这种能够观测到的稳定性对于我们去观察和理解一个系统非常重要。
该课程主要介绍了轨道稳定性和状态稳定性的含义和区别,通过大量的例子,详细介绍了状态稳定性判断的两种主要方法,李雅普诺夫函数和线性稳定性分析方法。
使用李雅普诺夫函数来判断定态的稳定性,具体方法是在定态附近找到它的李雅普诺夫函数,之后根据这个函数对时间演化的性质,进而判断系统的稳定性。由于李雅普诺夫函数是一个构造的方法,很多时候求解它会比较困难,使用起来具有一定的局限性。由于提出了一个相对简单且程序化的方法,线性稳定性判断的规则。
本中文词条由舒寒参与编译,思无涯咿呀咿呀编辑,欢迎在讨论页面留言。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。