双重差分
此词条暂由彩云小译翻译,翻译字数共2136,未经人工整理和审校,带来阅读不便,请见谅。
Difference in differences (DID[1] or DD[2]) is a statistical technique used in econometrics and quantitative research in the social sciences that attempts to mimic an experimental research design using observational study data, by studying the differential effect of a treatment on a 'treatment group' versus a 'control group' in a natural experiment.[3] It calculates the effect of a treatment (i.e., an explanatory variable or an independent variable) on an outcome (i.e., a response variable or dependent variable) by comparing the average change over time in the outcome variable for the treatment group to the average change over time for the control group. Although it is intended to mitigate the effects of extraneous factors and selection bias, depending on how the treatment group is chosen, this method may still be subject to certain biases (e.g., mean regression, reverse causality and omitted variable bias).
Difference in differences (DID or DD) is a statistical technique used in econometrics and quantitative research in the social sciences that attempts to mimic an experimental research design using observational study data, by studying the differential effect of a treatment on a 'treatment group' versus a 'control group' in a natural experiment. It calculates the effect of a treatment (i.e., an explanatory variable or an independent variable) on an outcome (i.e., a response variable or dependent variable) by comparing the average change over time in the outcome variable for the treatment group to the average change over time for the control group. Although it is intended to mitigate the effects of extraneous factors and selection bias, depending on how the treatment group is chosen, this method may still be subject to certain biases (e.g., mean regression, reverse causality and omitted variable bias).
差异的差异(DID 或 DD)是一种统计技术,用于计量经济学和社会科学的定量研究,试图模拟实验研究设计使用观察性研究数据,通过研究治疗组和对照组在自然实验中的差异效果。它通过比较治疗组治疗结果变量随时间的平均变化和对照组治疗结果变量随时间的平均变化,计算治疗结果(即解释变量或自变量)对结果(即反应变量或因变量)的影响。虽然这种方法的目的是减轻外来因素和选择偏差的影响,取决于如何选择治疗组,但这种方法仍然可能受到某些偏差的影响(例如,平均回归、反向因果关系和省略变量偏差)。
In contrast to a time-series estimate of the treatment effect on subjects (which analyzes differences over time) or a cross-section estimate of the treatment effect (which measures the difference between treatment and control groups), difference in differences uses panel data to measure the differences, between the treatment and control group, of the changes in the outcome variable that occur over time.
In contrast to a time-series estimate of the treatment effect on subjects (which analyzes differences over time) or a cross-section estimate of the treatment effect (which measures the difference between treatment and control groups), difference in differences uses panel data to measure the differences, between the treatment and control group, of the changes in the outcome variable that occur over time.
与受试者治疗效果的时间序列估计(分析随时间的差异)或治疗效果的横断面估计(衡量治疗组和对照组之间的差异)不同,治疗组和对照组之间的差异使用面板数据来衡量随时间发生的结果变量变化的差异。
General definition
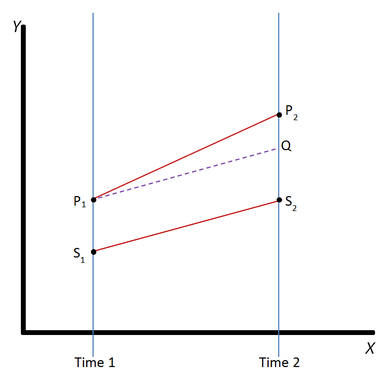
Difference in differences requires data measured from a treatment group and a control group at two or more different time periods, specifically at least one time period before "treatment" and at least one time period after "treatment." In the example pictured, the outcome in the treatment group is represented by the line P and the outcome in the control group is represented by the line S. The outcome (dependent) variable in both groups is measured at time 1, before either group has received the treatment (i.e., the independent or explanatory variable), represented by the points P1 and S1. The treatment group then receives or experiences the treatment and both groups are again measured at time 2. Not all of the difference between the treatment and control groups at time 2 (that is, the difference between P2 and S2) can be explained as being an effect of the treatment, because the treatment group and control group did not start out at the same point at time 1. DID therefore calculates the "normal" difference in the outcome variable between the two groups (the difference that would still exist if neither group experienced the treatment), represented by the dotted line Q. (Notice that the slope from P1 to Q is the same as the slope from S1 to S2.) The treatment effect is the difference between the observed outcome (P2) and the "normal" outcome (the difference between P2 and Q).
thumb|upright=1.3 Difference in differences requires data measured from a treatment group and a control group at two or more different time periods, specifically at least one time period before "treatment" and at least one time period after "treatment." In the example pictured, the outcome in the treatment group is represented by the line P and the outcome in the control group is represented by the line S. The outcome (dependent) variable in both groups is measured at time 1, before either group has received the treatment (i.e., the independent or explanatory variable), represented by the points P1 and S1. The treatment group then receives or experiences the treatment and both groups are again measured at time 2. Not all of the difference between the treatment and control groups at time 2 (that is, the difference between P2 and S2) can be explained as being an effect of the treatment, because the treatment group and control group did not start out at the same point at time 1. DID therefore calculates the "normal" difference in the outcome variable between the two groups (the difference that would still exist if neither group experienced the treatment), represented by the dotted line Q. (Notice that the slope from P1 to Q is the same as the slope from S1 to S2.) The treatment effect is the difference between the observed outcome (P2) and the "normal" outcome (the difference between P2 and Q).
= = 一般定义 = = 拇指 | 直立 = 1.3差异需要治疗组和对照组在两个或两个以上不同时间段测量数据,特别是在“治疗”前至少一个时间段和“治疗”后至少一个时间段在上图的例子中,治疗组的结果用线条 p 表示,对照组的结果用线条 s 表示。两组的结果(因变)变量在时间1测量,在任何一组接受治疗(即,独立或解释变量) ,代表点 p1和 S1。治疗组然后接受或经历治疗,两组再次测量时间2。治疗组和对照组在时间2时的差异(即 p2和 s2的差异)并非都可以解释为治疗的效果,因为治疗组和对照组在时间1时没有在同一时间开始。因此,DID 计算了两组之间结果变量的“正常”差异(如果两组都没有经历治疗,这种差异仍然存在) ,以虚线 q 表示。(注意 p1至 q 的斜率与 s1至 s2的斜率相同。)治疗效果是观察结果(P2)与“正常”结果(p2与 q 之间的差异)之间的差异。
Formal definition
Formal definition
= 正式定义 =
Consider the model
Consider the model
考虑一下这个模型
- [math]\displaystyle{ y_{it} ~=~ \gamma_{s(i)} + \lambda_t + \delta I(\dots) + \varepsilon_{it} }[/math]
- y_{it} ~=~ \gamma_{s(i)} + \lambda_t + \delta I(\dots) + \varepsilon_{it}
- y _ { it } ~ = ~ gamma _ { s (i)} + lambda _ t + delta i (dots) + varepsilon _ { it }
where [math]\displaystyle{ y_{it} }[/math] is the dependent variable for individual [math]\displaystyle{ i }[/math] and time [math]\displaystyle{ t }[/math], [math]\displaystyle{ s(i) }[/math] is the group to which [math]\displaystyle{ i }[/math] belongs (i.e. the treatment or the control group), and [math]\displaystyle{ I(\dots) }[/math] is short-hand for the dummy variable equal to 1 when the event described in [math]\displaystyle{ (\dots) }[/math] is true, and 0 otherwise. In the plot of time versus [math]\displaystyle{ Y }[/math] by group, [math]\displaystyle{ \gamma_s }[/math] is the vertical intercept for the graph for [math]\displaystyle{ s }[/math], and [math]\displaystyle{ \lambda_t }[/math] is the time trend shared by both groups according to the parallel trend assumption (see Assumptions below). [math]\displaystyle{ \delta }[/math] is the treatment effect, and [math]\displaystyle{ \varepsilon_{it} }[/math] is the residual term.
where y_{it} is the dependent variable for individual i and time t, s(i) is the group to which i belongs (i.e. the treatment or the control group), and I(\dots) is short-hand for the dummy variable equal to 1 when the event described in (\dots) is true, and 0 otherwise. In the plot of time versus Y by group, \gamma_s is the vertical intercept for the graph for s, and \lambda_t is the time trend shared by both groups according to the parallel trend assumption (see Assumptions below). \delta is the treatment effect, and \varepsilon_{it} is the residual term.
其中 y _ { it }是个体 i 的因变量,时间 t,s (i)是我所属的组(即。治疗或控制组) ,和 i (点)是短期的虚拟变量等于1时,所描述的事件(点)为真,否则为0。在时间与 y 的分组图中,gamma _ s 是 s 的垂直截距,而 lambda _ t 是两组根据平行趋势假设共享的时间趋势(见下文的假设)。Δ 是治疗效果,varepsilon _ { it }是残余效果。
Consider the average of the dependent variable and dummy indicators by group and time:
Consider the average of the dependent variable and dummy indicators by group and time:
考虑按组别和时间分列的因变量和虚拟指标的平均值:
- [math]\displaystyle{ \begin{align} n_s & = \text{ number of individuals in group } s \\ \overline{y}_{st} & = \frac{1}{n_s} \sum_{i=1}^n y_{it} \ I(s(i) ~=~ s), \\ \overline{\gamma}_s & = \frac{1}{n_s} \sum_{i=1}^n \gamma_{s(i)} \ I(s(i) ~=~ s) ~=~ \gamma_s, \\ \overline{\lambda}_{st} & = \frac{1}{n_s} \sum_{i=1}^n \lambda_t \ I(s(i) ~=~ s) ~=~ \lambda_t, \\ D_{st} & = \frac{1}{n_s} \sum_{i=1}^n I(s(i) ~=~\text{ treatment, } t \text{ in after period}) \ I(s(i) ~=~ s) ~=~ I(s ~=~\text{ treatment, } t \text{ in after period}) , \\ \overline{\varepsilon}_{st} & = \frac{1}{n_s} \sum_{i=1}^n \varepsilon_{it} \ I(s(i) ~=~ s), \end{align} }[/math]
\begin{align} n_s & = \text{ number of individuals in group } s \\ \overline{y}_{st} & = \frac{1}{n_s} \sum_{i=1}^n y_{it} \ I(s(i) ~=~ s), \\ \overline{\gamma}_s & = \frac{1}{n_s} \sum_{i=1}^n \gamma_{s(i)} \ I(s(i) ~=~ s) ~=~ \gamma_s, \\ \overline{\lambda}_{st} & = \frac{1}{n_s} \sum_{i=1}^n \lambda_t \ I(s(i) ~=~ s) ~=~ \lambda_t, \\ D_{st} & = \frac{1}{n_s} \sum_{i=1}^n I(s(i) ~=~\text{ treatment, } t \text{ in after period}) \ I(s(i) ~=~ s) ~=~ I(s ~=~\text{ treatment, } t \text{ in after period}) , \\ \overline{\varepsilon}_{st} & = \frac{1}{n_s} \sum_{i=1}^n \varepsilon_{it} \ I(s(i) ~=~ s), \end{align}
开始{ align } n _ s & = text { number of individuals in group } s overline { y }{ st } & = frac {1}{ n _ s } sum { i = 1} ^ n y _ it } i (s (i) ~ = ~ s) ,overline { gamma _ s & = frac {1}{ n _ s } sum { i = 1 ^ n _ γ { s (i)} i (s (i) ~ = ~ s) = ~ gamma _ s,1} ^ n lambda _ t i (s (i) ~ = ~ s) ~ = ~ lambda _ t,1} ^ n i (s (i) ~ = ~ text { in after period }) i (s (i) ~ = ~ i (s ~ = ~ text { treatment,}) ,在这里输入译文在这里输入译文在这里输入译文在这里输入译文在这里输入译文
and suppose for simplicity that [math]\displaystyle{ s=1,2 }[/math] and [math]\displaystyle{ t=1,2 }[/math]. Note that [math]\displaystyle{ D_{st} }[/math] is not random; it just encodes how the groups and the periods are labeled. Then
and suppose for simplicity that s=1,2 and t=1,2. Note that D_{st} is not random; it just encodes how the groups and the periods are labeled. Then
为了简单起见,假设 s = 1,2和 t = 1,2。请注意 d _ { st }不是随机的,它只是对组和周期的标记方式进行编码。然后
- [math]\displaystyle{ \begin{align} & (\overline{y}_{11} - \overline{y}_{12}) - (\overline{y}_{21} - \overline{y}_{22}) \\[6pt] = {} & \big[ (\gamma_1 + \lambda_1 + \delta D_{11} + \overline{\varepsilon}_{11}) - (\gamma_1 + \lambda_2 + \delta D_{12} + \overline{\varepsilon}_{12}) \big] \\ & \qquad {} - \big[ (\gamma_2 + \lambda_1 + \delta D_{21} + \overline{\varepsilon}_{21}) - (\gamma_2 + \lambda_2 + \delta D_{22} + \overline{\varepsilon}_{22}) \big] \\[6pt] = {} & \delta (D_{11} - D_{12}) + \delta(D_{22} - D_{21}) + \overline{\varepsilon}_{11} - \overline{\varepsilon}_{12} + \overline{\varepsilon}_{22} - \overline{\varepsilon}_{21}. \end{align} }[/math]
\begin{align} & (\overline{y}_{11} - \overline{y}_{12}) - (\overline{y}_{21} - \overline{y}_{22}) \\[6pt] = {} & \big[ (\gamma_1 + \lambda_1 + \delta D_{11} + \overline{\varepsilon}_{11}) - (\gamma_1 + \lambda_2 + \delta D_{12} + \overline{\varepsilon}_{12}) \big] \\ & \qquad {} - \big[ (\gamma_2 + \lambda_1 + \delta D_{21} + \overline{\varepsilon}_{21}) - (\gamma_2 + \lambda_2 + \delta D_{22} + \overline{\varepsilon}_{22}) \big] \\[6pt] = {} & \delta (D_{11} - D_{12}) + \delta(D_{22} - D_{21}) + \overline{\varepsilon}_{11} - \overline{\varepsilon}_{12} + \overline{\varepsilon}_{22} - \overline{\varepsilon}_{21}. \end{align}
开始{ align } & (overline { y } _ {11}-overline { y } _ {12})-(overline { y } _ {21}-overline { y } _ {22})[6 pt ] = {} & big[(gamma _ 1 + lambda _ 1 + delta d _ {11} + overline { varepsilon } _ {11})-(gamma _ 1 + lambda _ 2 + delta d _ {12} + overline { varepsilon } _ {12}) big ]大[(gamma _ 2 + lambda _ 1 + delta d _ {21} + overline { varepsilon }{21})-(gamma _ 2 + lambda _ 2 + delta d _ {22} + overline { varepsilon }{22})[6 pt ] = {} & delta (d _ {11}-d _ {12}) + delta(d _ {22}-d _ {21})+ overline { varepsilon } _ {11}-overline { varepsilon } _{12} + overline { varepsilon } _ {22}-overline { varepsilon } _ {21}.结束{ align }
The strict exogeneity assumption then implies that
The strict exogeneity assumption then implies that
严格外生性假设则意味着
- [math]\displaystyle{ \operatorname{E} \left [ (\overline{y}_{11} - \overline{y}_{12}) - (\overline{y}_{21} - \overline{y}_{22}) \right ] ~=~ \delta (D_{11} - D_{12}) + \delta(D_{22} - D_{21}). }[/math]
- \operatorname{E} \left [ (\overline{y}_{11} - \overline{y}_{12}) - (\overline{y}_{21} - \overline{y}_{22}) \right ] ~=~ \delta (D_{11} - D_{12}) + \delta(D_{22} - D_{21}).
- 操作数名{ e }左[(上行{ y } _ {11}-上行{ y } _ {12})-(上行{ y } _ {21}-上行{ y } _ {22})右] ~ = ~ delta (d _ {11}-d _ {12}) + delta (d _ {22}-d _ {21})。
Without loss of generality, assume that [math]\displaystyle{ s = 2 }[/math] is the treatment group, and [math]\displaystyle{ t = 2 }[/math] is the after period, then [math]\displaystyle{ D_{22}=1 }[/math] and [math]\displaystyle{ D_{11}=D_{12}=D_{21}=0 }[/math], giving the DID estimator
Without loss of generality, assume that s = 2 is the treatment group, and t = 2 is the after period, then D_{22}=1 and D_{11}=D_{12}=D_{21}=0, giving the DID estimator
不失一般性,假设 s = 2是治疗组,t = 2是后期,那么 d {22} = 1,d {11} = d {12} = d {21} = 0,给出 DID 估计量
- [math]\displaystyle{ \hat{\delta} ~=~ (\overline{y}_{11} - \overline{y}_{12}) - (\overline{y}_{21} - \overline{y}_{22}), }[/math]
- \hat{\delta} ~=~ (\overline{y}_{11} - \overline{y}_{12}) - (\overline{y}_{21} - \overline{y}_{22}),
- hat { delta } ~ = ~ (overline { y } _ {11}-overline { y } _ {12})-(overline { y } _ {21}-overline { y } _ {22}) ,
which can be interpreted as the treatment effect of the treatment indicated by [math]\displaystyle{ D_{st} }[/math]. Below it is shown how this estimator can be read as a coefficient in an ordinary least squares regression. The model described in this section is over-parametrized; to remedy that, one of the coefficients for the dummy variables can be set to 0, for example, we may set [math]\displaystyle{ \gamma_1 = 0 }[/math].
which can be interpreted as the treatment effect of the treatment indicated by D_{st}. Below it is shown how this estimator can be read as a coefficient in an ordinary least squares regression. The model described in this section is over-parametrized; to remedy that, one of the coefficients for the dummy variables can be set to 0, for example, we may set \gamma_1 = 0.
这可以解释为 d _ { st }所指的治疗效果。下面展示了如何将这个估计量解读为一般最小平方法回归中的一个系数。本节描述的模型是过参数化的; 为了补救这一点,可以将虚拟变量的一个系数设置为0,例如,我们可以设置 gamma _ 1 = 0。
Assumptions
Assumptions
= 假设 =
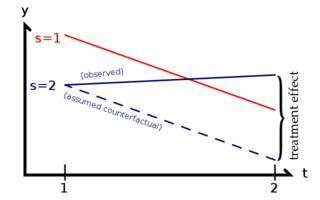
right|thumb|320px| Illustration of the parallel trend assumption
右 | 拇指 | 320px | 平行趋势假设的说明
All the assumptions of the OLS model apply equally to DID. In addition, DID requires a parallel trend assumption. The parallel trend assumption says that [math]\displaystyle{ \lambda_2 - \lambda_1 }[/math] are the same in both [math]\displaystyle{ s=1 }[/math] and [math]\displaystyle{ s=2 }[/math]. Given that the formal definition above accurately represents reality, this assumption automatically holds. However, a model with [math]\displaystyle{ \lambda_{st} ~:~ \lambda_{22} - \lambda_{21} \neq \lambda_{12} - \lambda_{11} }[/math] may well be more realistic. In order to increase the likelihood of the parallel trend assumption holding, a difference-in-difference approach is often combined with matching.[4] This involves 'Matching' known 'treatment' units with simulated counterfactual 'control' units: characteristically equivalent units which did not receive treatment. By defining the Outcome Variable as a temporal difference (change in observed outcome between pre- and posttreatment periods), and Matching multiple units in a large sample on the basis of similar pre-treatment histories, the resulting ATE (i.e. the ATT: Average Treatment Effect for the Treated) provides a robust difference-in-difference estimate of treatment effects. This serves two statistical purposes: firstly, conditional on pre-treatment covariates, the parallel trends assumption is likely to hold; and secondly, this approach reduces dependence on associated ignorability assumptions necessary for valid inference.
All the assumptions of the OLS model apply equally to DID. In addition, DID requires a parallel trend assumption. The parallel trend assumption says that \lambda_2 - \lambda_1 are the same in both s=1 and s=2. Given that the formal definition above accurately represents reality, this assumption automatically holds. However, a model with \lambda_{st} ~:~ \lambda_{22} - \lambda_{21} \neq \lambda_{12} - \lambda_{11} may well be more realistic. In order to increase the likelihood of the parallel trend assumption holding, a difference-in-difference approach is often combined with matching. This involves 'Matching' known 'treatment' units with simulated counterfactual 'control' units: characteristically equivalent units which did not receive treatment. By defining the Outcome Variable as a temporal difference (change in observed outcome between pre- and posttreatment periods), and Matching multiple units in a large sample on the basis of similar pre-treatment histories, the resulting ATE (i.e. the ATT: Average Treatment Effect for the Treated) provides a robust difference-in-difference estimate of treatment effects. This serves two statistical purposes: firstly, conditional on pre-treatment covariates, the parallel trends assumption is likely to hold; and secondly, this approach reduces dependence on associated ignorability assumptions necessary for valid inference.
所有 OLS 模型的假设都同样适用于分离性人工智能。此外,分离性人格障碍还需要一个平行的趋势假设。类似的趋势假设认为 lambda _ 2-lambda _ 1在 s = 1和 s = 2中都是相同的。鉴于上面的正式定义准确地代表了现实,这个假设自动成立。然而,一个带有 lambda { st } ~ : ~ lambda {22}-lambda {21} neq lambda {12}-lambda {11}的模型可能更加现实。为了增加并行趋势假设的可能性,经常采用差分差分法与匹配相结合的方法。这包括将已知的“处理”单位与模拟的反事实“控制”单位进行“匹配”: 特征性地相当于没有得到处理的单位。通过定义结果变量为一个时间差异(治疗前后观察结果的变化) ,并根据相似的前处理历史在大样本中匹配多个单位,得出的自动测试结果(即:。ATT: 治疗的平均治疗效果)提供了治疗效果的稳健差别估计。这样做有两个统计目的: 第一,基于预处理协变量,平行趋势假设很可能成立; 第二,这种方法减少了对有效推断所必需的相关可忽略性假设的依赖。
As illustrated to the right, the treatment effect is the difference between the observed value of y and what the value of y would have been with parallel trends, had there been no treatment. The Achilles' heel of DID is when something other than the treatment changes in one group but not the other at the same time as the treatment, implying a violation of the parallel trend assumption.
As illustrated to the right, the treatment effect is the difference between the observed value of y and what the value of y would have been with parallel trends, had there been no treatment. The Achilles' heel of DID is when something other than the treatment changes in one group but not the other at the same time as the treatment, implying a violation of the parallel trend assumption.
如右图所示,处理效果是观察到的 y 值与如果没有处理的话 y 值的平行趋势之间的差值。分离性人格障碍的致命弱点是当治疗以外的某些因素在治疗的同时改变了一个组,而不是另一个组,这意味着违反了平行趋势假设。
To guarantee the accuracy of the DID estimate, the composition of individuals of the two groups is assumed to remain unchanged over time. When using a DID model, various issues that may compromise the results, such as autocorrelation[5] and Ashenfelter dips, must be considered and dealt with.
To guarantee the accuracy of the DID estimate, the composition of individuals of the two groups is assumed to remain unchanged over time. When using a DID model, various issues that may compromise the results, such as autocorrelation and Ashenfelter dips, must be considered and dealt with.
为了保证分离性人格障碍评估的准确性,两组个体的组成被假定在一段时间内保持不变。在使用 DID 模型时,必须考虑和处理可能影响结果的各种问题,如自相关和 Ashenfelter 倾斜。
Implementation
Implementation
= 实现 =
The DID method can be implemented according to the table below, where the lower right cell is the DID estimator.
The DID method can be implemented according to the table below, where the lower right cell is the DID estimator.
DID 方法可以根据下表实现,其中右下角的单元格是 DID 估计器。
| [math]\displaystyle{ y_{st} }[/math] | [math]\displaystyle{ s=2 }[/math] | [math]\displaystyle{ s=1 }[/math] | Difference |
|---|---|---|---|
| [math]\displaystyle{ t=2 }[/math] | [math]\displaystyle{ y_{22} }[/math] | [math]\displaystyle{ y_{12} }[/math] | [math]\displaystyle{ y_{12}-y_{22} }[/math] |
| [math]\displaystyle{ t=1 }[/math] | [math]\displaystyle{ y_{21} }[/math] | [math]\displaystyle{ y_{11} }[/math] | [math]\displaystyle{ y_{11}-y_{21} }[/math] |
| Change | [math]\displaystyle{ y_{21}-y_{22} }[/math] | [math]\displaystyle{ y_{11}-y_{12} }[/math] | [math]\displaystyle{ (y_{11}-y_{21})-(y_{12}-y_{22}) }[/math] |
| y_{st} | s=2 | s=1 | Difference |
|---|---|---|---|
| t=2 | y_{22} | y_{12} | y_{12}-y_{22} |
| t=1 | y_{21} | y_{11} | y_{11}-y_{21} |
| Change | y_{21}-y_{22} | y_{11}-y_{12} | (y_{11}-y_{21})-(y_{12}-y_{22}) |
| 开始! !2! !1! !Difference | |||
|---|---|---|---|
| t=2 | y_{22} | y_{12} | y_{12}-y_{22} |
| t=1 | y_{21} | y_{11} | y_{11}-y_{21} |
| Change | y_{21}-y_{22} | y_{11}-y_{12} | (y_{11}-y_{21})-(y_{12}-y_{22}) |
Running a regression analysis gives the same result. Consider the OLS model
Running a regression analysis gives the same result. Consider the OLS model
跑一个回归分析也会得到同样的结果。考虑 OLS 模型
- [math]\displaystyle{ y ~=~ \beta_0 + \beta_1 T + \beta_2 S + \beta_3 (T \cdot S) + \varepsilon }[/math]
- y ~=~ \beta_0 + \beta_1 T + \beta_2 S + \beta_3 (T \cdot S) + \varepsilon
Y ~ = ~ beta _ 0 + beta _ 1 t + beta _ 2 s + beta _ 3(t cdot s) + varepsilon
where [math]\displaystyle{ T }[/math] is a dummy variable for the period, equal to [math]\displaystyle{ 1 }[/math] when [math]\displaystyle{ t=2 }[/math], and [math]\displaystyle{ S }[/math] is a dummy variable for group membership, equal to [math]\displaystyle{ 1 }[/math] when [math]\displaystyle{ s=2 }[/math]. The composite variable [math]\displaystyle{ (T \cdot S) }[/math] is a dummy variable indicating when [math]\displaystyle{ S=T=1 }[/math]. Although it is not shown rigorously here, this is a proper parametrization of the model formal definition, furthermore, it turns out that the group and period averages in that section relate to the model parameter estimates as follows
where T is a dummy variable for the period, equal to 1 when t=2, and S is a dummy variable for group membership, equal to 1 when s=2. The composite variable (T \cdot S) is a dummy variable indicating when S=T=1. Although it is not shown rigorously here, this is a proper parametrization of the model formal definition, furthermore, it turns out that the group and period averages in that section relate to the model parameter estimates as follows
其中 t 是周期的虚拟变量,当 t = 2时等于1,s 是组成员关系的虚拟变量,当 s = 2时等于1。复合变量(tcdot s)是一个哑变量,表示当 s = t = 1时。虽然这里没有严格地显示出来,但是这是模型形式定义的一个适当的参数化,而且,这一节中的群和周期平均值与模型参数估计有关,如下所示
- [math]\displaystyle{ \begin{align} \hat{\beta}_0 & = \widehat{E}(y \mid T=0,~ S=0) \\[8pt] \hat{\beta}_1 & = \widehat{E}(y \mid T=1,~ S=0) - \widehat{E}(y \mid T=0,~ S=0) \\[8pt] \hat{\beta}_2 & = \widehat{E}(y \mid T=0,~ S=1) - \widehat{E}(y \mid T=0,~ S=0) \\[8pt] \hat{\beta}_3 & = \big[\widehat{E}(y \mid T=1,~ S=1) - \widehat{E}(y \mid T=0,~ S=1)\big] \\ & \qquad {} - \big[\widehat{E}(y \mid T=1,~ S=0) - \widehat{E}(y \mid T=0,~ S=0)\big], \end{align} }[/math]
\begin{align} \hat{\beta}_0 & = \widehat{E}(y \mid T=0,~ S=0) \\[8pt] \hat{\beta}_1 & = \widehat{E}(y \mid T=1,~ S=0) - \widehat{E}(y \mid T=0,~ S=0) \\[8pt] \hat{\beta}_2 & = \widehat{E}(y \mid T=0,~ S=1) - \widehat{E}(y \mid T=0,~ S=0) \\[8pt] \hat{\beta}_3 & = \big[\widehat{E}(y \mid T=1,~ S=1) - \widehat{E}(y \mid T=0,~ S=1)\big] \\ & \qquad {} - \big[\widehat{E}(y \mid T=1,~ S=0) - \widehat{E}(y \mid T=0,~ S=0)\big], \end{align}
\begin{align} \hat{\beta}_0 & = \widehat{E}(y \mid T=0,~ S=0) \\[8pt] \hat{\beta}_1 & = \widehat{E}(y \mid T=1,~ S=0) - \widehat{E}(y \mid T=0,~ S=0) \\[8pt] \hat{\beta}_2 & = \widehat{E}(y \mid T=0,~ S=1) - \widehat{E}(y \mid T=0,~ S=0) \\[8pt] \hat{\beta}_3 & = \big[\widehat{E}(y \mid T=1,~ S=1) - \widehat{E}(y \mid T=0,~ S=1)\big] \\ & \qquad {} - \big[\widehat{E}(y \mid T=1,~ S=0) - \widehat{E}(y \mid T=0,~ S=0)\big], \end{align}
where [math]\displaystyle{ \widehat{E}(\dots \mid \dots ) }[/math] stands for conditional averages computed on the sample, for example, [math]\displaystyle{ T=1 }[/math] is the indicator for the after period, [math]\displaystyle{ S=0 }[/math] is an indicator for the control group. Note that [math]\displaystyle{ \hat{\beta}_1 }[/math] is an estimate of the counterfactual rather than the impact of the control group. The control group is often used as a proxy for the counterfactual (see, Synthetic control method for a deeper understanding of this point). Thereby, [math]\displaystyle{ \hat{\beta}_1 }[/math] can be interpreted as the impact of both the control group and the intervention's (treatment's) counterfactual. Similarly, [math]\displaystyle{ \hat{\beta}_2 }[/math], due to the parallel trend assumption, is also the same differential between the treatment and control group in [math]\displaystyle{ T=1 }[/math]. The above descriptions should not be construed to imply the (average) effect of only the control group, for [math]\displaystyle{ \hat{\beta}_1 }[/math], or only the difference of the treatment and control groups in the pre-period, for [math]\displaystyle{ \hat{\beta}_2 }[/math]. As in Card and Krueger, below, a first (time) difference of the outcome variable [math]\displaystyle{ (\Delta Y_i = Y_{i,1} - Y_{i,0}) }[/math] eliminates the need for time-trend (i.e., [math]\displaystyle{ \hat{\beta}_1 }[/math]) to form an unbiased estimate of [math]\displaystyle{ \hat{\beta}_3 }[/math], implying that [math]\displaystyle{ \hat{\beta}_1 }[/math] is not actually conditional on the treatment or control group.[6] Consistently, a difference among the treatment and control groups would eliminate the need for treatment differentials (i.e., [math]\displaystyle{ \hat{\beta}_2 }[/math]) to form an unbiased estimate of [math]\displaystyle{ \hat{\beta}_3 }[/math]. This nuance is important to understand when the user believes (weak) violations of parallel pre-trend exist or in the case of violations of the appropriate counterfactual approximation assumptions given the existence of non-common shocks or confounding events. To see the relation between this notation and the previous section, consider as above only one observation per time period for each group, then
where \widehat{E}(\dots \mid \dots ) stands for conditional averages computed on the sample, for example, T=1 is the indicator for the after period, S=0 is an indicator for the control group. Note that \hat{\beta}_1 is an estimate of the counterfactual rather than the impact of the control group. The control group is often used as a proxy for the counterfactual (see, Synthetic control method for a deeper understanding of this point). Thereby, \hat{\beta}_1 can be interpreted as the impact of both the control group and the intervention's (treatment's) counterfactual. Similarly, \hat{\beta}_2, due to the parallel trend assumption, is also the same differential between the treatment and control group in T=1 . The above descriptions should not be construed to imply the (average) effect of only the control group, for \hat{\beta}_1, or only the difference of the treatment and control groups in the pre-period, for \hat{\beta}_2. As in Card and Krueger, below, a first (time) difference of the outcome variable (\Delta Y_i = Y_{i,1} - Y_{i,0}) eliminates the need for time-trend (i.e., \hat{\beta}_1) to form an unbiased estimate of \hat{\beta}_3, implying that \hat{\beta}_1 is not actually conditional on the treatment or control group. Consistently, a difference among the treatment and control groups would eliminate the need for treatment differentials (i.e., \hat{\beta}_2) to form an unbiased estimate of \hat{\beta}_3. This nuance is important to understand when the user believes (weak) violations of parallel pre-trend exist or in the case of violations of the appropriate counterfactual approximation assumptions given the existence of non-common shocks or confounding events. To see the relation between this notation and the previous section, consider as above only one observation per time period for each group, then
其中 widehat { e }(点中点)代表样本计算的条件平均值,例如,t = 1是后期的指标,s = 0是对照组的指标。请注意,hat { beta }1是对反事实的估计,而不是对照组的影响。控制组经常被用作反事实的代理(见,综合控制方法,以便更深入地理解这一点)。因此,hat { beta } _ 1可以被解释为对照组和干预(治疗)的反事实影响。同样,由于平行趋势假设,t = 1的治疗组和对照组之间也存在相同的差异。上述描述不应该被解释为仅仅是对照组的(平均)效应,对于 hat { beta } _ 1,或者仅仅是治疗组和对照组在前期的差别,对 hat { beta } _ 2。正如 Card 和 Krueger 所说,结果变量(Delta y _ i = y _ { i,1}-y _ { i,0})的第一次(时间)差消除了时间趋势(即 hat { beta } _ 1)对 hat { beta } _ 3的无偏估计,这意味着 hat { beta } _ 1实际上并不取决于治疗或控制组。一致地,治疗组和对照组之间的差异将消除治疗差异(即,hat { beta } _ 2)的需要,以形成一个 hat { beta } _ 3的公正估计。这种细微差别对于理解用户何时认为存在(弱)违反平行预趋势的情况,或在存在非常见冲击或混杂事件的情况下违反适当的反事实近似假设的情况,很重要。为了看到这个符号和前面的章节之间的关系,考虑上面每个小组每个时间段只有一个观察值,然后
- [math]\displaystyle{ \begin{align} \widehat{E}(y \mid T=1,~ S=0) & = \widehat{E}(y \mid \text{ after period, control}) \\ [3pt] \\ & = \frac{ \widehat{E}(y \ I(\text{ after period, control}) )}{ \widehat{P}(\text{ after period, control})} \\ [3pt] \\ & = \frac{ \sum_{i=1}^n y_{i,\text{after}} I(i \text{ in control}) } { n_{\text{control}} } = \overline{y}_{\text{control, after}} \\ [3pt] \\ & = \overline{y}_{\text{12}} \end{align} }[/math]
and so on for other values of [math]\displaystyle{ T }[/math] and [math]\displaystyle{ S }[/math], which is equivalent to
\begin{align}
\widehat{E}(y \mid T=1,~ S=0) & = \widehat{E}(y \mid \text{ after period, control}) \\
[3pt] \\ & = \frac{ \widehat{E}(y \ I(\text{ after period, control}) )}{ \widehat{P}(\text{ after period, control})} \\ [3pt] \\ & = \frac{ \sum_{i=1}^n y_{i,\text{after}} I(i \text{ in control}) } { n_{\text{control}} } = \overline{y}_{\text{control, after}} \\ [3pt] \\ & = \overline{y}_{\text{12}} \end{align}
and so on for other values of T and S, which is equivalent to
开始{ align } widehat { e }(y mid t = 1,~ s = 0) & = widehat { e }(y mid text { after period,control })[3 pt ] & = frac { widehat { e }(text { after period,control }(text { after period,control })}(y i (text { after period,control }))}{ wideh { widehat { p }(text }(after period,control }))[3 pt ]和 = frac { sum { i = 1} ^ nY _ { i,text { after } i (i text { in control })}{ n _ { text { control }} = overline { y }{ text { control,after }[3 pt ] & = overline { y }{ text {12}} end { align }等于
- [math]\displaystyle{ \hat{\beta}_3 ~=~ (y_{11} - y_{21}) - (y_{12} - y_{22}). }[/math]
- \hat{\beta}_3 ~=~ (y_{11} - y_{21}) - (y_{12} - y_{22}).
3 ~ = ~ (y _ {11}-y _ {21})-(y _ {12}-y _ {22}).
But this is the expression for the treatment effect that was given in the formal definition and in the above table.
But this is the expression for the treatment effect that was given in the formal definition and in the above table.
但这是正式定义和上表中给出的治疗效果的表达式。
Card and Krueger (1994) example
Card and Krueger (1994) example
= Card and Krueger (1994) example =
Consider one of the most famous DID studies, the Card and Krueger article on minimum wage in New Jersey, published in 1994.[7] Card and Krueger compared employment in the fast food sector in New Jersey and in Pennsylvania, in February 1992 and in November 1992, after New Jersey's minimum wage rose from $4.25 to $5.05 in April 1992. Observing a change in employment in New Jersey only, before and after the treatment, would fail to control for omitted variables such as weather and macroeconomic conditions of the region. By including Pennsylvania as a control in a difference-in-differences model, any bias caused by variables common to New Jersey and Pennsylvania is implicitly controlled for, even when these variables are unobserved. Assuming that New Jersey and Pennsylvania have parallel trends over time, Pennsylvania's change in employment can be interpreted as the change New Jersey would have experienced, had they not increased the minimum wage, and vice versa. The evidence suggested that the increased minimum wage did not induce a decrease in employment in New Jersey, contrary to what some economic theory would suggest. The table below shows Card & Krueger's estimates of the treatment effect on employment, measured as FTEs (or full-time equivalents). Card and Krueger estimate that the $0.80 minimum wage increase in New Jersey led to a 2.75 FTE increase in employment.
Consider one of the most famous DID studies, the Card and Krueger article on minimum wage in New Jersey, published in 1994. Card and Krueger compared employment in the fast food sector in New Jersey and in Pennsylvania, in February 1992 and in November 1992, after New Jersey's minimum wage rose from $4.25 to $5.05 in April 1992. Observing a change in employment in New Jersey only, before and after the treatment, would fail to control for omitted variables such as weather and macroeconomic conditions of the region. By including Pennsylvania as a control in a difference-in-differences model, any bias caused by variables common to New Jersey and Pennsylvania is implicitly controlled for, even when these variables are unobserved. Assuming that New Jersey and Pennsylvania have parallel trends over time, Pennsylvania's change in employment can be interpreted as the change New Jersey would have experienced, had they not increased the minimum wage, and vice versa. The evidence suggested that the increased minimum wage did not induce a decrease in employment in New Jersey, contrary to what some economic theory would suggest. The table below shows Card & Krueger's estimates of the treatment effect on employment, measured as FTEs (or full-time equivalents). Card and Krueger estimate that the $0.80 minimum wage increase in New Jersey led to a 2.75 FTE increase in employment.
想想最著名的分离性人格障碍研究之一,卡德和克鲁格在1994年发表的关于新泽西州最低工资的文章。Card 和 Krueger 比较了1992年2月和1992年11月新泽西州最低工资从4.25美元上升到5.05美元后新泽西州和宾夕法尼亚州快餐部门的就业情况。仅仅观察治疗前后新泽西州就业情况的变化,就无法控制该地区天气和宏观经济状况等被忽略的变量。通过将宾夕法尼亚州作为差异中的差异模型的控制对象,任何由新泽西州和宾夕法尼亚州共有的变量引起的偏差都会被隐式控制,即使这些变量没有被观察到。假设新泽西州和宾夕法尼亚州随着时间的推移有类似的趋势,宾夕法尼亚州就业的变化可以被解释为新泽西州会经历的变化,如果他们没有提高最低工资,反之亦然。有证据表明,提高最低工资并没有导致新泽西州就业率的下降,这与一些经济理论所表明的情况恰恰相反。下面的表格显示了 Card & Krueger 对就业治疗效果的估计,以 fte (或全职等价物)衡量。卡德和克鲁格估计,新泽西州0.80美元的最低工资增长导致了2.75美元的就业率增长。
| New Jersey | Pennsylvania | Difference | |
|---|---|---|---|
| February | 20.44 | 23.33 | −2.89 |
| November | 21.03 | 21.17 | −0.14 |
| Change | 0.59 | −2.16 | 2.75 |
| New Jersey | Pennsylvania | Difference | |
|---|---|---|---|
| February | 20.44 | 23.33 | −2.89 |
| November | 21.03 | 21.17 | −0.14 |
| Change | 0.59 | −2.16 | 2.75 |
| 新泽西! !宾夕法尼亚!Difference | |||
|---|---|---|---|
| February | 20.44 | 23.33 | −2.89 |
| November | 21.03 | 21.17 | −0.14 |
| Change | 0.59 | −2.16 | 2.75 |
See also
- Design of experiments
- Average treatment effect
- Synthetic control method
实验设计平均处理效果综合控制方法
References
- ↑ Abadie, A. (2005). "Semiparametric difference-in-differences estimators". Review of Economic Studies. 72 (1): 1–19. CiteSeerX 10.1.1.470.1475. doi:10.1111/0034-6527.00321.
- ↑ Bertrand, M.; Duflo, E.; Mullainathan, S. (2004). "How Much Should We Trust Differences-in-Differences Estimates?" (PDF). Quarterly Journal of Economics. 119 (1): 249–275. doi:10.1162/003355304772839588. S2CID 470667.
- ↑ Angrist, J. D.; Pischke, J. S. (2008). Mostly Harmless Econometrics: An Empiricist's Companion. Princeton University Press. pp. 227–243. ISBN 978-0-691-12034-8. https://books.google.com/books?id=ztXL21Xd8v8C&pg=PA227.
- ↑ Basu, Pallavi; Small, Dylan (2020). "Constructing a More Closely Matched Control Group in a Difference-in-Differences Analysis: Its Effect on History Interacting with Group Bias" (PDF). Observational Studies. 6: 103–130.
- ↑ Bertrand, Marianne; Duflo, Esther; Mullainathan, Sendhil (2004). "How Much Should We Trust Differences-In-Differences Estimates?" (PDF). Quarterly Journal of Economics. 119 (1): 249–275. doi:10.1162/003355304772839588. S2CID 470667.
- ↑ Card, David; Krueger, Alan B. (1994). "Minimum Wages and Employment: A Case Study of the Fast-Food Industry in New Jersey and Pennsylvania". American Economic Review. 84 (4): 772–793. JSTOR 2118030.
- ↑ Card, David; Krueger, Alan B. (1994). "Minimum Wages and Employment: A Case Study of the Fast-Food Industry in New Jersey and Pennsylvania". American Economic Review. 84 (4): 772–793. JSTOR 2118030.
Further reading
- Angrist, J. D.; Pischke, J. S. (2008). Mostly Harmless Econometrics: An Empiricist's Companion. Princeton University Press. pp. 227–243. ISBN 978-0-691-12034-8. https://books.google.com/books?id=ztXL21Xd8v8C&pg=PA227.
- Cameron, Arthur C.; Trivedi, Pravin K. (2005). Microeconometrics: Methods and Applications. Cambridge university press. pp. 768–772. doi:10.1017/CBO9780511811241. ISBN 9780521848053. https://api.semanticscholar.org/CorpusID:120313863.
- Imbens, Guido W.; Wooldridge, Jeffrey M. (2009). "Recent Developments in the Econometrics of Program Evaluation". Journal of Economic Literature. 47 (1): 5–86. doi:10.1257/jel.47.1.5.
- Bakija, Jon; Heim, Bradley (August 2008). "How Does Charitable Giving Respond to Incentives and Income? Dynamic Panel Estimates Accounting for Predictable Changes in Taxation". NBER Working Paper No. 14237. doi:10.3386/w14237.
- Conley, T.; Taber, C. (July 2005). "Inference with 'Difference in Differences' with a Small Number of Policy Changes". NBER Technical Working Paper No. 312. doi:10.3386/t0312.
= 进一步阅读 =
External links
- Difference in Difference Estimation, Healthcare Economist website
- Difference in Difference Estimation, Healthcare Economist website
= = 外部链接 =
- 差异估计差异,医疗经济学家网站
Category:Econometric modeling
Category:Regression analysis
Category:Design of experiments
Category:Observational study
Category:Causal inference
Category:Subtraction
类别: 计量经济学模型类别: 回归分析类别: 实验设计类别: 观察性研究类别: 因果推理类别: 减法
This page was moved from wikipedia:en:Difference in differences. Its edit history can be viewed at 双重差分/edithistory