断点回归

此词条暂由彩云小译翻译，翻译字数共2115，未经人工整理和审校，带来阅读不便，请见谅。

In statistics, econometrics, political science, epidemiology, and related disciplines, a regression discontinuity design (RDD) is a quasi-experimental pretest-posttest design that aims to determine the causal effects of interventions by assigning a cutoff or threshold above or below which an intervention is assigned. By comparing observations lying closely on either side of the threshold, it is possible to estimate the average treatment effect in environments in which randomisation is unfeasible. However, it remains impossible to make true causal inference with this method alone, as it does not automatically reject causal effects by any potential confounding variable. First applied by Donald Thistlethwaite and Donald Campbell to the evaluation of scholarship programs, the RDD has become increasingly popular in recent years. Recent study comparisons of randomised controlled trials (RCTs) and RDDs have empirically demonstrated the internal validity of the design.

In statistics, econometrics, political science, epidemiology, and related disciplines, a regression discontinuity design (RDD) is a quasi-experimental pretest-posttest design that aims to determine the causal effects of interventions by assigning a cutoff or threshold above or below which an intervention is assigned. By comparing observations lying closely on either side of the threshold, it is possible to estimate the average treatment effect in environments in which randomisation is unfeasible. However, it remains impossible to make true causal inference with this method alone, as it does not automatically reject causal effects by any potential confounding variable. First applied by Donald Thistlethwaite and Donald Campbell to the evaluation of scholarship programs, the RDD has become increasingly popular in recent years. Recent study comparisons of randomised controlled trials (RCTs) and RDDs have empirically demonstrated the internal validity of the design.

在统计学、计量经济学、政治科学、流行病学和相关学科中，回归不连续性设计是一种准实验性的前后测设计，其目的是通过设定一个临界值或阈值来确定干预的因果效应。通过比较紧密放置在阈值两侧的观测值，可以估计在随机化不可行的环境中的平均处理效果。然而，仅用这种方法仍然不可能做出真正的因果推断，因为它不会自动排除任何潜在的混杂变量的因果效应。最初是由唐纳德 · 西斯特维特和唐纳德 · 坎贝尔应用于奖学金项目的评估，近年来 RDD 变得越来越受欢迎。最近的随机对照试验(rct)和 RDDs 的研究比较已经实验性地证明了设计的内部效度。

编辑后：

在统计学、计量经济学、政治学、流行病学和相关学科中，断点回归是一种准实验性的前后侧设计，其目的是通过设定一个临界值或阈值，其两侧即为干预效果的分配。通过比较临近阈值两侧的观测值，可以估计在随机化不可行的条件下的平均处理效果。然而，仅使用这种方法仍然不能做出完全的因果推断，因为它不会自动排除任何潜在混杂变量的因果效应。断点回归最初由唐纳德·西斯尔思韦特和唐纳德·坎贝尔应用于奖学金项目的评估，近年来越来越受到欢迎。最近的随机对照实验(RCTs)和RDDs的研究比较已经经验性地证明了该设计的内部有效性。

Example

The intuition behind the RDD is well illustrated using the evaluation of merit-based scholarships. The main problem with estimating the causal effect of such an intervention is the homogeneity of performance to the assignment of treatment (e.g. scholarship award). Since high-performing students are more likely to be awarded the merit scholarship and continue performing well at the same time, comparing the outcomes of awardees and non-recipients would lead to an upward bias of the estimates. Even if the scholarship did not improve grades at all, awardees would have performed better than non-recipients, simply because scholarships were given to students who were performing well ex-ante.

The intuition behind the RDD is well illustrated using the evaluation of merit-based scholarships. The main problem with estimating the causal effect of such an intervention is the homogeneity of performance to the assignment of treatment (e.g. scholarship award). Since high-performing students are more likely to be awarded the merit scholarship and continue performing well at the same time, comparing the outcomes of awardees and non-recipients would lead to an upward bias of the estimates. Even if the scholarship did not improve grades at all, awardees would have performed better than non-recipients, simply because scholarships were given to students who were performing well ex-ante.

= = 实例 = = 通过对基于成绩的奖学金的评估，可以很好地说明 RDD 背后的直觉。估计这种干预的因果效应的主要问题是对待遇分配的表现的同质性(例如:。奖学金)。由于表现优异的学生更有可能获得优异奖学金，同时继续表现良好，因此比较获奖学生和非获奖学生的成绩，估计数字会偏向上方。即使奖学金根本没有提高成绩，获奖者的成绩也会比没有获奖者的成绩要好，这仅仅是因为奖学金是颁发给事先表现良好的学生。

编辑后：

= = 实例 = =通过对基于成绩的奖学金的评估，可以很好地说明RDD背后的直觉。估计这种干预的因果效应的主要问题是分配至处理组的样本的表现具有同质性（如：奖学金）。因为表现优异的学生更有可能获得优异奖学金，同时这些学生在未来将继续表现良好，因此比较获奖学金学生和未获奖学金学生的成绩，会使估计结果偏高。即使奖学金根本没有提高学生的成绩，获奖学金学生的成绩也会比没有获奖学金的成绩要好，这是因为奖学金是颁发给原本就表现良好的学生。

Despite the absence of an experimental design, an RDD can exploit exogenous characteristics of the intervention to elicit causal effects. If all students above a given grade — for example 80% — are given the scholarship, it is possible to elicit the local treatment effect by comparing students around the 80% cut-off. The intuition here is that a student scoring 79% is likely to be very similar to a student scoring 81% — given the pre-defined threshold of 80%. However, one student will receive the scholarship while the other will not. Comparing the outcome of the awardee (treatment group) to the counterfactual outcome of the non-recipient (control group) will hence deliver the local treatment effect.

Despite the absence of an experimental design, an RDD can exploit exogenous characteristics of the intervention to elicit causal effects. If all students above a given grade — for example 80% — are given the scholarship, it is possible to elicit the local treatment effect by comparing students around the 80% cut-off. The intuition here is that a student scoring 79% is likely to be very similar to a student scoring 81% — given the pre-defined threshold of 80%. However, one student will receive the scholarship while the other will not. Comparing the outcome of the awardee (treatment group) to the counterfactual outcome of the non-recipient (control group) will hence deliver the local treatment effect.

尽管缺乏一个实验设计，一个 RDD 可以利用干预的外部特征来引出因果效应。如果给予所有特定年级以上的学生(例如80%)奖学金，就有可能通过比较80% 分界线附近的学生，得出当地的治疗效果。这里的直觉是，一个得分79% 的学生很可能与一个得分81% 的学生非常相似ーー假设预先设定的阈值是80% 。但是，一个学生将获得奖学金，而另一个学生不会。将受奖者(治疗组)的治疗结果与非受奖者(对照组)的反事实治疗结果进行比较，可以达到局部治疗效果。

Methodology

The two most common approaches to estimation using an RDD are non-parametric and parametric (normally polynomial regression).

The two most common approaches to estimation using an RDD are non-parametric and parametric (normally polynomial regression).

= = 方法 = = 使用 RDD 进行估计的两种最常见的方法是非参数和参数(通常是多项式回归)。

= = 非参数估计 = =

The most common non-parametric method used in the RDD context is a local linear regression. This is of the form:

The most common non-parametric method used in the RDD context is a local linear regression. This is of the form:

在 RDD 上下文中使用的最常见的非参数方法是局部线性回归。下面是这样的形式:

[math]\displaystyle{ Y = \alpha + \tau D + \beta_{1}(X-c) + \beta_{2}D(X-c) + \varepsilon , }[/math]

Y = \alpha + \tau D + \beta_{1}(X-c) + \beta_{2}D(X-c) + \varepsilon ,

Y = \alpha + \tau D + \beta_{1}(X-c) + \beta_{2}D(X-c) + \varepsilon ,

where [math]\displaystyle{ c }[/math] is the treatment cutoff and [math]\displaystyle{ D }[/math] is a binary variable equal to one if [math]\displaystyle{ X \ge c }[/math]. Letting [math]\displaystyle{ h }[/math] be the bandwidth of data used, we have [math]\displaystyle{ c - h \le X \le c + h }[/math]. Different slopes and intercepts fit data on either side of the cutoff. Typically either a rectangular kernel (no weighting) or a triangular kernel are used. Research favours the triangular kernel, but the rectangular kernel has a more straightforward interpretation.

where c is the treatment cutoff and D is a binary variable equal to one if X \ge c. Letting h be the bandwidth of data used, we have c - h \le X \le c + h . Different slopes and intercepts fit data on either side of the cutoff. Typically either a rectangular kernel (no weighting) or a triangular kernel are used. Research favours the triangular kernel, but the rectangular kernel has a more straightforward interpretation.

其中 c 是处理截止值，d 是一个二进制变量，如果 x ge c 是一个二进制变量，如果 h 是所用数据的带宽，我们有 c-h le x le c + h。不同的斜坡和拦截符合截止线两侧的数据。通常使用矩形核心(不加权)或三角形核心。研究倾向于三角形核，而矩形核有更直接的解释。

The major benefit of using non-parametric methods in an RDD is that they provide estimates based on data closer to the cut-off, which is intuitively appealing. This reduces some bias that can result from using data farther away from the cutoff to estimate the discontinuity at the cutoff. More formally, local linear regressions are preferred because they have better bias properties and have better convergence. However, the use of both types of estimation, if feasible, is a useful way to argue that the estimated results do not rely too heavily on the particular approach taken.

The major benefit of using non-parametric methods in an RDD is that they provide estimates based on data closer to the cut-off, which is intuitively appealing. This reduces some bias that can result from using data farther away from the cutoff to estimate the discontinuity at the cutoff. More formally, local linear regressions are preferred because they have better bias properties and have better convergence. However, the use of both types of estimation, if feasible, is a useful way to argue that the estimated results do not rely too heavily on the particular approach taken.

在 RDD 中使用非参数方法的主要好处是，它们提供基于更接近截止值的数据的估计，这是直观上的吸引力。这减少了一些偏差，这些偏差可以通过使用距离截止点更远的数据来估计截止点的不连续性。更正式地说，局部线性回归是首选，因为它们具有更好的偏差性质和更好的收敛性。然而，如果可行的话，使用这两种类型的估计是一种有用的方法，可以证明估计的结果并不过分依赖所采取的特定方法。

Parametric estimation

An example of a parametric estimation is:

[math]\displaystyle{ Y = \alpha + \beta_1 x_i + \beta_2 c_i + \beta_3 c_i^2 + \beta_4 c_i^3 + \varepsilon , }[/math]

where

[math]\displaystyle{ x_i= \begin{cases} 1\text{ if }c_i \geq \bar{c}\\ 0\text{ if }c_i \lt \bar{c} \end{cases} }[/math]

and [math]\displaystyle{ \bar{c} }[/math] is the treatment cutoff. Note that the polynomial part can be shortened or extended according to the needs.

An example of a parametric estimation is:

Y = \alpha + \beta_1 x_i + \beta_2 c_i + \beta_3 c_i^2 + \beta_4 c_i^3 + \varepsilon ,

where

x_i= \begin{cases} 1\text{ if }c_i \geq \bar{c}\\ 0\text{ if }c_i < \bar{c} \end{cases}

and \bar{c} is the treatment cutoff. Note that the polynomial part can be shortened or extended according to the needs.

= = = 参数估计 = = = 参数估计的一个例子是: y = alpha + beta _ 1 x _ i + beta _ 2 c _ i + beta _ 3 c _ i ^ 2 + beta _ 4 c _ i ^ 3 + varepsilon，其中: x _ i = begin { cases }1 text { if } c _ i geq bar { c }0 text { if } c _ i < bar { c } end { cases }和 bar { c }是处理方法。注意，多项式部分可根据需要缩短或扩展。

Other examples

• Policies in which treatment is determined by an age eligibility criterion (e.g. pensions, minimum legal drinking age).
• Elections in which one politician wins by a marginal majority.
• Placement scores within education that sort students into treatment programs.

• Policies in which treatment is determined by an age eligibility criterion (e.g. pensions, minimum legal drinking age).
• Elections in which one politician wins by a marginal majority.
• Placement scores within education that sort students into treatment programs.

= = 其他例子 =

• 由年龄资格标准确定待遇的政策(例如:。养老金，最低法定饮酒年龄)。
• 一个政治家以微弱多数获胜的选举。
• 将学生分类到治疗项目中的教育分数。

Required assumptions

Regression discontinuity design requires that all potentially relevant variables besides the treatment variable and outcome variable be continuous at the point where the treatment and outcome discontinuities occur. One sufficient, though not necessary, condition is if the treatment assignment is "as good as random" at the threshold for treatment. If this holds, then it guarantees that those who just barely received treatment are comparable to those who just barely did not receive treatment, as treatment status is effectively random.

Regression discontinuity design requires that all potentially relevant variables besides the treatment variable and outcome variable be continuous at the point where the treatment and outcome discontinuities occur. One sufficient, though not necessary, condition is if the treatment assignment is "as good as random" at the threshold for treatment. If this holds, then it guarantees that those who just barely received treatment are comparable to those who just barely did not receive treatment, as treatment status is effectively random.

= = 所需假设 = = 回归不连续性设计要求除了处理变量和结果变量之外，所有潜在相关变量在处理和结果不连续性发生的点都是连续的。一个充分但不是必要的条件是，治疗分配在治疗门槛处是“和随机分配一样好”。如果这种说法成立，那么它保证了那些刚刚接受治疗的人与那些刚刚没有接受治疗的人是可比的，因为治疗状况实际上是随机的。

Treatment assignment at the threshold can be "as good as random" if there is randomness in the assignment variable and the agents considered (individuals, firms, etc.) cannot perfectly manipulate their treatment status. For example, suppose the treatment is passing an exam, where a grade of 50% is required. In this case, this example is a valid regression discontinuity design so long as grades are somewhat random, due either to the randomness of grading or randomness of student performance.

Treatment assignment at the threshold can be "as good as random" if there is randomness in the assignment variable and the agents considered (individuals, firms, etc.) cannot perfectly manipulate their treatment status. For example, suppose the treatment is passing an exam, where a grade of 50% is required. In this case, this example is a valid regression discontinuity design so long as grades are somewhat random, due either to the randomness of grading or randomness of student performance.

如果在分配变量和被考虑的代理人(个人、公司等)中存在随机性，在阈值处理分配可以“和随机性一样好”并不能完全控制他们的治疗状况。例如，假设治疗通过了一个考试，其中50% 的等级是必需的。在这种情况下，这个例子是一个有效的回归不连续设计，只要成绩是随机的，无论是由于随机的评分或随机的学生表现。

Students must not also be able to perfectly manipulate their grade so as to determine their treatment status perfectly. Two examples include students being able to convince teachers to "mercy pass" them, or students being allowed to retake the exam until they pass. In the former case, those students who barely fail but are able to secure a "mercy pass" may differ from those who just barely fail but cannot secure a "mercy pass". This leads to selection bias, as the treatment and control groups now differ. In the latter case, some students may decide to retake the exam, stopping once they pass. This also leads to selection bias since only some students will decide to retake the exam.

Students must not also be able to perfectly manipulate their grade so as to determine their treatment status perfectly. Two examples include students being able to convince teachers to "mercy pass" them, or students being allowed to retake the exam until they pass. In the former case, those students who barely fail but are able to secure a "mercy pass" may differ from those who just barely fail but cannot secure a "mercy pass". This leads to selection bias, as the treatment and control groups now differ. In the latter case, some students may decide to retake the exam, stopping once they pass. This also leads to selection bias since only some students will decide to retake the exam.

学生也不能完美地操纵他们的分数，从而完美地确定他们的治疗状态。两个例子包括学生能够说服老师“仁慈通过”他们，或学生被允许重新参加考试，直到他们通过。在前一种情况下，那些几乎不及格但是能够获得“宽恕通行证”的学生可能不同于那些几乎不及格但是不能获得“宽恕通行证”的学生。这导致了选择偏差，因为治疗组和控制组现在不同。在后一种情况下，一些学生可能决定重新参加考试，一旦通过就停止。这也导致了选择偏见，因为只有一些学生会决定重新参加考试。

Testing the validity of the assumptions

It is impossible to definitively test for validity if agents are able to determine their treatment status perfectly. However, some tests can provide evidence that either supports or discounts the validity of the regression discontinuity design.

It is impossible to definitively test for validity if agents are able to determine their treatment status perfectly. However, some tests can provide evidence that either supports or discounts the validity of the regression discontinuity design.

如果代理人能够完美地确定他们的待遇状态，那么就不可能确切地检验这些假设的有效性。然而，一些测试可以提供证据支持或折扣回归不连续设计的有效性。

Density test

McCrary (2008) density test on data from Lee, Moretti, and Butler (2004).

McCrary (2008) suggested examining the density of observations of the assignment variable. Suppose there is a discontinuity in the density of the assignment variable at the threshold for treatment. In this case, this may suggest that some agents were able to manipulate their treatment status perfectly.

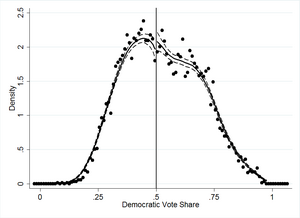
thumb|McCrary (2008) density test on data from Lee, Moretti, and Butler (2004). McCrary (2008) suggested examining the density of observations of the assignment variable. Suppose there is a discontinuity in the density of the assignment variable at the threshold for treatment. In this case, this may suggest that some agents were able to manipulate their treatment status perfectly.

= = = = 密度测试 = = = 拇指 | McCrary (2008)对 Lee，Moretti 和 Butler (2004)的数据进行密度测试。McCrary (2008)建议检查分配变量的观测密度。假设在处理的阈值处赋值变量的密度存在不连续性。在这种情况下，这可能表明一些药物能够完美地操纵他们的治疗状态。

For example, if several students are able to get a "mercy pass", then there will be more students who just barely passed the exam than who just barely failed. Similarly, if students are allowed to retake the exam until they pass, then there will be a similar result. In both cases, this will likely show up when the density of exam grades is examined. "Gaming the system" in this manner could bias the treatment effect estimate.

For example, if several students are able to get a "mercy pass", then there will be more students who just barely passed the exam than who just barely failed. Similarly, if students are allowed to retake the exam until they pass, then there will be a similar result. In both cases, this will likely show up when the density of exam grades is examined. "Gaming the system" in this manner could bias the treatment effect estimate.

例如，如果一些学生能够获得“安乐死”，那么就会有更多的学生勉强通过考试而不是勉强通过考试。同样，如果允许学生重新参加考试直到他们通过，那么也会有类似的结果。在这两种情况下，这可能会显示时，密度的考试成绩检查。以这种方式“博弈系统”可能会对治疗效果的估计产生偏差。

Continuity of observable variables

Since the validity of the regression discontinuity design relies on those who were just barely treated being the same as those who were just barely not treated, it makes sense to examine if these groups are similarly based on observable variables. For the earlier example, one could test if those who just barely passed have different characteristics (demographics, family income, etc.) than those who just barely failed. Although some variables may differ for the two groups based on random chance, most of these variables should be the same.

Since the validity of the regression discontinuity design relies on those who were just barely treated being the same as those who were just barely not treated, it makes sense to examine if these groups are similarly based on observable variables. For the earlier example, one could test if those who just barely passed have different characteristics (demographics, family income, etc.) than those who just barely failed. Although some variables may differ for the two groups based on random chance, most of these variables should be the same.

= = = = 连续的可观察变量 = = = = 由于回归不连续性设计的有效性依赖于那些仅仅被视为与那些仅仅被视为没有被视为一样的人，所以检查这些群体是否同样基于可观察的变量是有意义的。对于前面的例子，我们可以测试那些刚刚通过考试的人是否具有不同的特征(人口统计学、家庭收入等等)而不是那些刚刚失败的人。虽然一些变量可能会因为随机机会的不同而有所不同，但大多数变量应该是相同的。

= = 伪造测试 = =

Predetermined variables

Similar to the continuity of observable variables, one would expect there to be continuity in predetermined variables at the treatment cutoff. Since these variables were determined before the treatment decision, treatment status should not affect them. Consider the earlier merit-based scholarship example. If the outcome of interest is future grades, then we would not expect the scholarship to affect previous grades. If a discontinuity in predetermined variables is present at the treatment cutoff, then this puts the validity of the regression discontinuity design into question.

Similar to the continuity of observable variables, one would expect there to be continuity in predetermined variables at the treatment cutoff. Since these variables were determined before the treatment decision, treatment status should not affect them. Consider the earlier merit-based scholarship example. If the outcome of interest is future grades, then we would not expect the scholarship to affect previous grades. If a discontinuity in predetermined variables is present at the treatment cutoff, then this puts the validity of the regression discontinuity design into question.

= = = = = 预定变量 = = = = = = 类似于可观测变量的连续性，预期在处理截止时预定变量会有连续性。由于这些变量是在治疗决定之前确定的，治疗状态不应该影响他们。考虑一下之前的基于成绩的奖学金例子。如果兴趣的结果是未来的成绩，那么我们不会期望奖学金会影响以前的成绩。如果预定变量的不连续性出现在处理截止点，那么这就使回归不连续设计的有效性成为问题。

Other discontinuities

If discontinuities are present at other points of the assignment variable, where these are not expected, then this may make the regression discontinuity design suspect. Consider the example of Carpenter and Dobkin (2011) who studied the effect of legal access to alcohol in the United States. As the access to alcohol increases at age 21, this leads to changes in various outcomes, such as mortality rates and morbidity rates. If mortality and morbidity rates also increase discontinuously at other ages, then it throws the interpretation of the discontinuity at age 21 into question.

If discontinuities are present at other points of the assignment variable, where these are not expected, then this may make the regression discontinuity design suspect. Consider the example of Carpenter and Dobkin (2011) who studied the effect of legal access to alcohol in the United States. As the access to alcohol increases at age 21, this leads to changes in various outcomes, such as mortality rates and morbidity rates. If mortality and morbidity rates also increase discontinuously at other ages, then it throws the interpretation of the discontinuity at age 21 into question.

= = = = = = = = = = = 如果在赋值变量的其他点存在不连续性，而这些不连续性是不可预期的，那么这可能使回归不连续性设计受到怀疑。以 Carpenter 和 Dobkin (2011)为例，他们研究了美国合法饮酒的影响。随着21岁人群接触酒精的机会增加，这会导致各种结果的改变，如死亡率和发病率。如果死亡率和发病率在其他年龄段也不连续地增加，那么21岁时对不连续性的解释就成为问题。

Inclusion and exclusion of covariates

If parameter estimates are sensitive to removing or adding covariates to the model, then this may cast doubt on the validity of the regression discontinuity design. A significant change may suggest that those who just barely got treatment to differ in these covariates from those who just barely did not get treatment. Including covariates would remove some of this bias. If a large amount of bias is present, and the covariates explain a significant amount of this, then their inclusion or exclusion would significantly change the parameter estimate.

If parameter estimates are sensitive to removing or adding covariates to the model, then this may cast doubt on the validity of the regression discontinuity design. A significant change may suggest that those who just barely got treatment to differ in these covariates from those who just barely did not get treatment. Including covariates would remove some of this bias. If a large amount of bias is present, and the covariates explain a significant amount of this, then their inclusion or exclusion would significantly change the parameter estimate.

= = = = = 协变量的包含和排除 = = = = = 如果参数估计对去除或增加模型的协变量很敏感，那么这可能会对回归不连续设计的有效性提出质疑。一个显著的变化可能表明那些刚刚得到治疗的人和那些刚刚没有得到治疗的人在这些协变量上有所不同。加入协变量可以消除一些这种偏见。如果存在大量的偏差，并且协变量可以解释大量的偏差，那么它们的包含或排除将显著改变参数估计。

Recent work has shown how to add covariates, under what conditions doing so is valid, and the potential for increased precision.

Recent work has shown how to add covariates, under what conditions doing so is valid, and the potential for increased precision.

最近的工作已经展示了如何添加协变量，在什么条件下这样做是有效的，以及提高精度的潜力。

Advantages

• When properly implemented and analysed, the RDD yields an unbiased estimate of the local treatment effect. The RDD can be almost as good as a randomised experiment in measuring a treatment effect.
• RDD, as a quasi-experiment, does not require ex-ante randomisation and circumvents ethical issues of random assignment.
• Well-executed RDD studies can generate treatment effect estimates similar to estimates from randomised studies.

• When properly implemented and analysed, the RDD yields an unbiased estimate of the local treatment effect. The RDD can be almost as good as a randomised experiment in measuring a treatment effect.
• RDD, as a quasi-experiment, does not require ex-ante randomisation and circumvents ethical issues of random assignment.
• Well-executed RDD studies can generate treatment effect estimates similar to estimates from randomised studies.

= =

• 当正确实施和分析时，RDD 产生了对局部处理效果的无偏估计。在测量治疗效果方面，RDD 几乎可以和随机实验一样好。
• RDD，作为一个准实验，不需要事先随机化，并规避随机分配的伦理问题。
• 良好执行的 RDD 研究可以产生类似于随机研究估计的治疗效果估计。

Disadvantages

• The estimated effects are only unbiased if the functional form of the relationship between the treatment and outcome is correctly modelled. The most popular caveats are non-linear relationships that are mistaken as a discontinuity.
• Contamination by other treatments. Suppose another treatment occurs at the same cutoff value of the same assignment variable. In that case, the measured discontinuity in the outcome variable may be partially attributed to this other treatment. For example, suppose a researcher wishes to study the impact of legal access to alcohol on mental health using a regression discontinuity design at the minimum legal drinking age. The measured impact could be confused with legal access to gambling, which may occur at the same age.

• The estimated effects are only unbiased if the functional form of the relationship between the treatment and outcome is correctly modelled. The most popular caveats are non-linear relationships that are mistaken as a discontinuity.
• Contamination by other treatments. Suppose another treatment occurs at the same cutoff value of the same assignment variable. In that case, the measured discontinuity in the outcome variable may be partially attributed to this other treatment. For example, suppose a researcher wishes to study the impact of legal access to alcohol on mental health using a regression discontinuity design at the minimum legal drinking age. The measured impact could be confused with legal access to gambling, which may occur at the same age.

= = 缺点 =

• 只有正确地模拟了治疗和结果之间的函数形式，估计的效果才是无偏的。最受欢迎的警告是被误认为是不连续的非线性关系。
• 受其他处理方法污染。假设在相同赋值变量的相同截止值处发生另一个处理。在这种情况下，测量的结果变量的不连续性可能部分归因于这个其他的治疗。例如，假设一位研究人员希望在法定最低饮酒年龄采用回归间断设计来研究合法饮酒对心理健康的影响。衡量的影响可能会与合法参与赌博相混淆，后者可能发生在同一年龄段。

= 扩展 =

Fuzzy RDD

The identification of causal effects hinges on the crucial assumption that there is indeed a sharp cut-off, around which there is a discontinuity in the probability of assignment from 0 to 1. In reality, however, cutoffs are often not strictly implemented (e.g. exercised discretion for students who just fell short of passing the threshold) and the estimates will hence be biased.

The identification of causal effects hinges on the crucial assumption that there is indeed a sharp cut-off, around which there is a discontinuity in the probability of assignment from 0 to 1. In reality, however, cutoffs are often not strictly implemented (e.g. exercised discretion for students who just fell short of passing the threshold) and the estimates will hence be biased.

= = = 模糊 RDD = = = 因果效应的确定取决于一个关键的假设，即确实存在一个急剧的截止点，在这个截止点周围存在着从0到1的分配概率的不连续性。然而，在现实中，切断通常不是严格执行的(例如:。对于刚刚未能通过门槛的学生行使酌情权) ，因此估计会有偏差。

In contrast to the sharp regression discontinuity design, a fuzzy regression discontinuity design (FRDD) does not require a sharp discontinuity in the probability of assignment. Still, it is applicable as long as the probability of assignment is different. The intuition behind it is related to the instrumental variable strategy and intention to treat.

In contrast to the sharp regression discontinuity design, a fuzzy regression discontinuity design (FRDD) does not require a sharp discontinuity in the probability of assignment. Still, it is applicable as long as the probability of assignment is different. The intuition behind it is related to the instrumental variable strategy and intention to treat.

与尖锐回归不连续设计相比，模糊回归不连续设计(FRDD)不要求分配概率尖锐不连续。尽管如此，只要分配的概率不同，它仍然是适用的。这背后的直觉与工具变量/治疗策略和治疗意图有关。

Regression kink design

When the assignment variable is continuous (e.g. student aid) and depends predictably on another observed variable (e.g. family income), one can identify treatment effects using sharp changes in the slope of the treatment function. This technique was coined regression kink design by Nielsen, Sørensen, and Taber (2010), though they cite similar earlier analyses. They write, "This approach resembles the regression discontinuity idea. Instead of a discontinuity of in the level of the stipend-income function, we have a discontinuity in the slope of the function." Rigorous theoretical foundations were provided by Card et al. (2012) and an empirical application by Bockerman et al. (2018).

When the assignment variable is continuous (e.g. student aid) and depends predictably on another observed variable (e.g. family income), one can identify treatment effects using sharp changes in the slope of the treatment function. This technique was coined regression kink design by Nielsen, Sørensen, and Taber (2010), though they cite similar earlier analyses. They write, "This approach resembles the regression discontinuity idea. Instead of a discontinuity of in the level of the stipend-income function, we have a discontinuity in the slope of the function." Rigorous theoretical foundations were provided by Card et al. (2012) and an empirical application by Bockerman et al. (2018).

= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =.学生资助) ，并可预见地取决于另一个观察到的变量(例如:。家庭收入) ，一个可以确定治疗效果利用急剧变化的斜率的治疗功能。这项技术被称为回归扭结设计，由尼尔森，s ø rensen 和 Taber (2010年) ，尽管他们引用了类似的早期分析。他们写道: “这种方法类似于回归不连续性的思想。我们没有看到津贴-收入函数水平的不连续性，而是看到了函数斜率的不连续性。”Card 等人提供了严格的理论基础。2012)和 Bockerman 等人的实证应用。(2018).

Note that regression kinks (or kinked regression) can also mean a type of segmented regression, which is a different type of analysis.

Note that regression kinks (or kinked regression) can also mean a type of segmented regression, which is a different type of analysis.

请注意，回归扭结(或扭结回归)也可以意味着一种分段回归，这是一种不同类型的分析。

Final Considerations

Final Considerations

最后的考虑

The RD design takes the shape of a quasi-experimental research design with a clear structure that is devoid of randomized experimental features. Several aspects deny the RD designs an allowance for a status quo. For instance, the designs often involve serious issues that do not offer room for random experiments. Besides, the design of the experiments depends on the accuracy of the modelling process and the relationship between inputs and outputs.

The RD design takes the shape of a quasi-experimental research design with a clear structure that is devoid of randomized experimental features. Several aspects deny the RD designs an allowance for a status quo. For instance, the designs often involve serious issues that do not offer room for random experiments. Besides, the design of the experiments depends on the accuracy of the modelling process and the relationship between inputs and outputs.

RD 设计采用准实验研究设计的形式，结构清晰，没有随机化的实验特征。有几个方面否定了研发人员对现状的宽容。例如，设计往往涉及严重的问题，不提供随机试验的空间。此外，实验的设计取决于建模过程的准确性和输入与输出之间的关系。

See also

• Quasi-experiment
• Design of quasi-experiments

• Quasi-experiment
• Design of quasi-experiments

= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

Further reading

• Angrist, J. D.; Pischke, J.-S. (2008). "Getting a Little Jumpy: Regression Discontinuity Designs". Mostly Harmless Econometrics: An Empiricist's Companion. Princeton University Press. pp. 251–268. ISBN 978-0-691-12035-5. 
• Cook, Thomas D. (2008). "'Waiting for Life to Arrive': A history of the regression-discontinuity design in Psychology, Statistics and Economics". Journal of Econometrics. 142 (2): 636–654. doi:10.1016/j.jeconom.2007.05.002.
• Imbens, Guido W.; Wooldridge, Jeffrey M. (2009). "Recent Developments in the Econometrics of Program Evaluation". Journal of Economic Literature. 47 (1): 5–86. doi:10.1257/jel.47.1.5.
• Maas, Iris L.; Nolte, Sandra; Walter, Otto B.; Berger, Thomas; Hautzinger, Martin (2017). "The regression discontinuity design showed to be a valid alternative to a randomized controlled trial for estimating treatment effects". Journal of Clinical Epidemiology. 82: 94–102. doi:10.1016/j.jclinepi.2016.11.008. PMID 27865902.

= 进一步阅读 =

External links

• Regression-Discontinuity Analysis at Research Methods Knowledge Base

• Regression-Discontinuity Analysis at Research Methods Knowledge Base

= = 外部链接 =

• 回归-研究方法知识库的不连续性分析

Category:Design of experiments Category:Econometric modeling Category:Regression analysis Category:Observational study

类别: 实验设计类别: 计量经济学模型类别: 回归分析类别: 观察性研究

This page was moved from wikipedia:en:Regression discontinuity design. Its edit history can be viewed at 断点回归/edithistory