气候模式

此词条暂由气象人翻译。

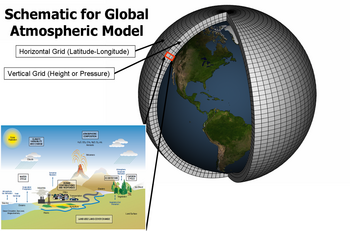
Climate models are systems of differential equations based on the basic laws of physics, fluid motion, and chemistry. To “run” a model, scientists divide the planet into a Three-dimensional grid, apply the basic equations, and evaluate the results. Atmospheric models calculate winds, heat transfer, radiation, relative humidity, and overland runoff  within each grid and evaluate interactions with neighboring points.

气候模型是基于物理、流体运动和化学基本定律的微分方程系统。 为了“运行”一个模型，科学家们将地球划分成一个三维网格，应用基本方程，并对结果进行评估。 大气模型计算每个网格内的风、热传递、辐射、相对湿度和地表径流，并评估与邻近点的相互作用。  

Climate models may be Numerical，and also qualitative (i.e. not numerical) .Qualitative Climate models are narratives, largely descriptive, of possible futures.

气候模式可以是数值的，也可以是定性的(即不是数值的)。定性的气候模型通常是对未来的可能描述。

Numerical climate models use quantitative methods to simulate the interactions of the important drivers of climate, including atmosphere, oceans, land surface and ice. They are used for a variety of purposes from study of the dynamics of the climate system to projections of future climate.

Quantitative climate models take account of incoming energy from the sun as short wave electromagnetic radiation, chiefly visible and short-wave (near) infrared, as well as outgoing long wave (far) infrared electromagnetic. An imbalance results in a change in temperature.

Quantitative models vary in complexity:

数值气候模型使用定量方法来模拟气候的重要驱动因素之间的相互作用，包括大气、海洋、陆地表面和冰。它们被用于从研究气候系统的动态到预测未来气候的各种目的。定量的气候模型考虑到来自太阳的入射能量为短波电磁辐射，主要是可见光和短波(近)红外线，以及外向长波(远)红外线电磁辐射。其不平衡导致温度的变化。

·A simple radiant heat transfer model treats the earth as a single point and averages outgoing energy. This can be expanded vertically (radiative-convective models) and/or horizontallyFinally, (coupled) atmosphere–ocean–sea ice global climate models solve the full equations for mass and energy transfer and radiant exchange.Other types of modelling can be interlinked, such as land use, in Earth System Models, allowing researchers to predict the interaction between climate and ecosystems.

定性模型复杂性各不相同:

一个简单的辐射热传递模型是将地球作为一个单点，对输出能量进行平均。(耦合的)大气-海洋-海冰全球气候模式解决了质量、能量转移和辐射交换的完整方程。在地球系统模型中，其他类型的模型可以相互关联，例如土地使用，使研究人员能够预测气候与生态系统之间的相互作用。

Climate models are systems of differential equations based on the basic laws of physics, fluid motion, and chemistry. To “run” a model, scientists divide the planet into a 3-dimensional grid, apply the basic equations, and evaluate the results. Atmospheric models calculate winds, heat transfer, radiation, relative humidity, and surface hydrology within each grid and evaluate interactions with neighboring points.

Box models= 盒子模型=

Schematic of a simple box model used to illustrate fluxes in geochemical cycles, showing a source (Q), sink (S) and reservoir (M)

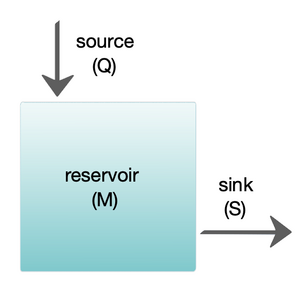
Box models are simplified versions of complex systems, reducing them to boxes (or reservoirs) linked by fluxes. The boxes are assumed to be mixed homogeneously. Within a given box, the concentration of any chemical species is therefore uniform. However, the abundance of a species within a given box may vary as a function of time due to the input to (or loss from) the box or due to the production, consumption or decay of this species within the box.

Box models are simplified versions of complex systems, reducing them to boxes (or reservoirs) linked by fluxes. The boxes are assumed to be mixed homogeneously. Within a given box, the concentration of any chemical species is therefore uniform. However, the abundance of a species within a given box may vary as a function of time due to the input to (or loss from) the box or due to the production, consumption or decay of this species within the box.

盒子模型是复杂系统的简化版本，将它们简化为通量连接的盒子(或水库)。假定这些盒子是均匀混合的。因此，在一个给定的盒子内，任何化学物质的浓度都是均匀的。然而，在一个给定的盒子内的一个物种的丰度可能会随着时间的变化而变化，这是由于盒子内的输入(或损失)或这个物种在盒子内的生产、消费或衰变所致。

Simple box models, i.e. box model with a small number of boxes whose properties (e.g. their volume) do not change with time, are often useful to derive analytical formulas describing the dynamics and steady-state abundance of a species. More complex box models are usually solved using numerical techniques.

Simple box models, i.e. box model with a small number of boxes whose properties (e.g. their volume) do not change with time, are often useful to derive analytical formulas describing the dynamics and steady-state abundance of a species. More complex box models are usually solved using numerical techniques.

简单的盒子模型，例如。盒子模型，有少量的盒子，它们的属性(例如:。它们的体积)不随时间变化，通常用于推导描述物种的动态和稳态丰度的解析公式。更复杂的箱模型通常用数值方法求解。

Box models are used extensively to model environmental systems or ecosystems and in studies of ocean circulation and the carbon cycle. They are instances of a multi-compartment model.

Box models are used extensively to model environmental systems or ecosystems and in studies of ocean circulation and the carbon cycle. They are instances of a multi-compartment model.

箱模型被广泛用于模拟环境系统或生态系统以及海洋环流和碳循环的研究。它们是多室模型的实例。

Zero-dimensional models= 零维模型 =

A very simple model of the radiative equilibrium of the Earth is

(1-a)S \pi r^2 = 4 \pi r^2 \epsilon \sigma T^4

where

• the left hand side represents the incoming energy from the Sun
• the right hand side represents the outgoing energy from the Earth, calculated from the Stefan–Boltzmann law assuming a model-fictive temperature, T, sometimes called the “equilibrium temperature of the Earth”, that is to be found.
• S is the solar constant – the incoming solar radiation per unit area—about 1367 W·m⁻²
• a is the Earth's average albedo, measured to be 0.3.
• r is Earth's radius—approximately 6.371×106m
• π is the mathematical constant (3.141...)
• σ is the Stefan–Boltzmann constant—approximately 5.67×10−8 J·K−4·m−2·s−1
• ε is the effective emissivity of earth, about 0.612

The constant πr² can be factored out, giving

(1-a)S = 4 \epsilon \sigma T^4

Solving for the temperature,

T = \sqrt[4]{ \frac{(1-a)S}{4 \epsilon \sigma}}

This yields an apparent effective average earth temperature of Convert. This is because the above equation represents the effective radiative temperature of the Earth (including the clouds and atmosphere).

• 一个非常简单的地球辐射平衡模型是： (1-a)S \pi r^2 = 4 \pi r^2 \epsilon \sigma T^4
• 左边代表来自太阳的能量。
• 右边代表来自地球的能量，根据 Stefan-Boltzmann 定律计算，假设模型假设温度T，有时称为“地球的平衡温度”。
• S是太阳常数，即单位面积内的入射太阳辐射约1367 W·m⁻²
• a 是地球的平均反照率，测量值为0.3。
• r 为地球半径ー大约6.371 × 106m
• π 为数学常数(3.141...)
• σ 为斯蒂芬-玻尔兹曼常数ー大约5.67 × 10^-8jk^-4m^-2s^-1
• ε 为地球的有效发射率，大约0.612

常数 πr2可以分解出来，给出

求解温度 , T = sqrt [4]{ frac {(1-a) s }{4 epsilon sigma }} 这样得到转换的表观有效地球平均温度。这是因为上面的方程代表了地球的有效辐射温度(包括云和大气)。

This very simple model is quite instructive. For example, it easily determines the effect on average earth temperature of changes in solar constant or change of albedo or effective earth emissivity.

这个非常简单的模型很有启发性。例如，它很容易确定太阳常数的变化或反照率或有效地球发射率的变化对平均地球温度的影响。

The average emissivity of the earth is readily estimated from available data. The emissivities of terrestrial surfaces are all in the range of 0.96 to 0.99 (except for some small desert areas which may be as low as 0.7). Clouds, however, which cover about half of the earth's surface, have an average emissivity of about 0.5 (which must be reduced by the fourth power of the ratio of cloud absolute temperature to average earth absolute temperature) and an average cloud temperature of about 模板:Convert. Taking all this properly into account results in an effective earth emissivity of about 0.64 (earth average temperature 模板:Convert).

地球的平均比辐射率很容易从现有数据中估计出来。陆地表面的放射系数均在0.96ー0.99之间(除少数小沙漠地区可能低至0.7)。然而，覆盖地球表面大约一半的云层，其平均发射率约为0.5(必须用云的绝对温度与地球平均绝对温度之比的四次方减少) ，而云的平均温度约为0.5。适当地考虑这些因素，得到的有效地球发射率约为0.64(地球平均温度)。

This simple model readily determines the effect of changes in solar output or change of earth albedo or effective earth emissivity on average earth temperature. It says nothing, however about what might cause these things to change. Zero-dimensional models do not address the temperature distribution on the earth or the factors that move energy about the earth.

这个简单的模型很容易确定太阳输出量的变化或地球反照率或有效地球发射率的变化对地球平均温度的影响。然而，它没有提到是什么可能导致这些事情发生改变。零维模型不能解释地球上的温度分布或者地球周围移动能量的因素。

Radiative-convective models= = 辐射-对流模式 =

The zero-dimensional model above, using the solar constant and given average earth temperature, determines the effective earth emissivity of long wave radiation emitted to space. This can be refined in the vertical to a one-dimensional radiative-convective model, which considers two processes of energy transport:

• upwelling and downwelling radiative transfer through atmospheric layers that both absorb and emit infrared radiation
• upward transport of heat by convection (especially important in the lower troposphere).

上述零维模型利用太阳常数和给定的地球平均温度，确定了向空间发射的长波辐射的有效地球发射率。这可以在垂直于一维辐射对流模式的方向上加以改进，该模式考虑两个能量输送过程:

• 通过大气层的上升流和下降辐射转移，这些大气层通过对流层吸收和释放红外线
• 向上传送热量(在对流层下部尤其重要)。

The radiative-convective models have advantages over the simple model: they can determine the effects of varying greenhouse gas concentrations on effective emissivity and therefore the surface temperature. But added parameters are needed to determine local emissivity and albedo and address the factors that move energy about the earth.

辐射-对流模式比简单模式有优点: 它们可以确定不同温室气体浓度对有效发射率的影响，因此也可以确定地表温度。但是需要增加参数来确定局部辐射系数和反照率，并解决地球周围能量移动的因素。

Effect of ice-albedo feedback on global sensitivity in a one-dimensional radiative-convective climate model.

冰反照率反馈对一维辐射对流气候模式全球敏感性的影响。

Higher-dimension models= = 高维模型 = =

The zero-dimensional model may be expanded to consider the energy transported horizontally in the atmosphere. This kind of model may well be zonally averaged. This model has the advantage of allowing a rational dependence of local albedo and emissivity on temperature – the poles can be allowed to be icy and the equator warm – but the lack of true dynamics means that horizontal transports have to be specified.

可以扩展零维模型以考虑大气中水平输送的能量。这种模型很可能是纬向平均的。这个模型的优点是允许局部反照率和辐射系数与温度有合理的依赖关系——两极可以是冰的，赤道可以是暖的——但缺乏真正的动力学，这意味着必须具体说明水平输送。

EMICs (Earth-system models of intermediate complexity)

Main article: Earth systems model of intermediate complexity

Depending on the nature of questions asked and the pertinent time scales, there are, on the one extreme, conceptual, more inductive models, and, on the other extreme, general circulation models operating at the highest spatial and temporal resolution currently feasible. Models of intermediate complexity bridge the gap. One example is the Climber-3 model. Its atmosphere is a 2.5-dimensional statistical-dynamical model with 7.5° × 22.5° resolution and time step of half a day; the ocean is MOM-3 (Modular Ocean Model) with a 3.75° × 3.75° grid and 24 vertical levels.

根据所提问题的性质和相关的时间尺度，在一个极端，概念上有更多的归纳模型，而在另一个极端，大气环流模型在最高的空间和时间解析度上运行，目前是可行的。中等复杂性模型弥补了这一差距。其中一个例子是 climber-3模型。其大气为2.5维统计动力学模式，分辨率为7.5 ° × 22.5 ° ，时间步长为半天，海洋为模块化海洋模式 MOM-3，网格为3.75 ° × 3.75 ° ，垂直高度为24 ° 。

GCMs (global climate models or general circulation models)

Main article: General circulation model

General Circulation Models (GCMs) discretise the equations for fluid motion and energy transfer and integrate these over time. Unlike simpler models, GCMs divide the atmosphere and/or oceans into grids of discrete "cells", which represent computational units. Unlike simpler models which make mixing assumptions, processes internal to a cell—such as convection—that occur on scales too small to be resolved directly are parameterised at the cell level, while other functions govern the interface between cells.

大气环流模式(GCMs)离散了流体运动和能量传递的方程，并随着时间的推移积分这些方程。与较简单的模型不同，大气环流模型将大气和/或海洋划分为代表计算单位的离散“单元”网格。与作出混合假设的简单模型不同，单元内部的过程(例如对流)在尺度太小而无法直接解决的情况下在单元层面上被参数化，而其他功能则控制单元之间的界面。

Atmospheric GCMs (AGCMs) model the atmosphere and impose sea surface temperatures as boundary conditions. Coupled atmosphere-ocean GCMs (AOGCMs, e.g. HadCM3, EdGCM, GFDL CM2.X, ARPEGE-Climat) combine the two models. The first general circulation climate model that combined both oceanic and atmospheric processes was developed in the late 1960s at the NOAA Geophysical Fluid Dynamics Laboratory AOGCMs represent the pinnacle of complexity in climate models and internalise as many processes as possible. However, they are still under development and uncertainties remain. They may be coupled to models of other processes, such as the carbon cycle, so as to better model feedback effects. Such integrated multi-system models are sometimes referred to as either "earth system models" or "global climate models."

大气层大气环流模式(AGCMs)模拟大气，并把海面温度作为边界条件。大气-海洋耦合大气环流模式。结合了这两个模型。第一个将海洋和大气过程结合在一起的大气环流气候模式是在20世纪60年代末由美国国家海洋和大气管理局的地球物理流体动力学实验室气候模式发展起来的，它代表了气候模式复杂性的顶峰，并且尽可能地内化了许多过程。然而，它们仍在发展之中，不确定性仍然存在。它们可以与碳循环等其他过程的模型耦合，以便更好地模拟反馈效应。这种综合的多系统模型有时被称为“地球系统模型”或“全球气候模型”

Research and development= 研究与开发 =

There are three major types of institution where climate models are developed, implemented and used:

• National meteorological services. Most national weather services have a climatology section.
• Universities. Relevant departments include atmospheric sciences, meteorology, climatology, and geography.
• National and international research laboratories. Examples include the National Center for Atmospheric Research (NCAR, in Boulder, Colorado, USA), the Geophysical Fluid Dynamics Laboratory (GFDL, in Princeton, New Jersey, USA), Los Alamos National Laboratory, the Hadley Centre for Climate Prediction and Research (in Exeter, UK), the Max Planck Institute for Meteorology in Hamburg, Germany, or the Laboratoire des Sciences du Climat et de l'Environnement (LSCE), France, to name but a few.

开发、实施和使用气候模型的机构主要有三类:

• 国家气象部门。大多数国家气象服务机构都有气候学部分。
• 大学。相关部门包括大气科学、气象学、气候学和地理学。
• 国家和国际研究实验室。例如，美国国家大气研究中心(NCAR，位于科罗拉多州的博尔德) ，美国地球物理流体动力学实验室研究所(GFDL，位于美国新泽西州的普林斯顿) ，洛斯阿拉莫斯国家实验室，哈德利气候预测与研究中心气象研究所(位于埃克塞特) ，德国汉堡的马克斯 · 普朗克气象研究所，或者法国的气候与环境科学实验室(LSCE)等等。

The World Climate Research Programme (WCRP), hosted by the World Meteorological Organization (WMO), coordinates research activities on climate modelling worldwide.

世界气候研究计划由世界气象组织气象组织主办，负责协调全球气候建模的研究活动。

A 2012 U.S. National Research Council report discussed how the large and diverse U.S. climate modeling enterprise could evolve to become more unified. Efficiencies could be gained by developing a common software infrastructure shared by all U.S. climate researchers, and holding an annual climate modeling forum, the report found.

2012年美国国家研究委员会的一份报告讨论了美国庞大而多样化的气候模拟事业如何能够进化得更加统一。报告发现，通过开发一个由所有美国气候研究人员共享的通用软件基础设施，并举办一个年度气候模型论坛，效率可以得到提高。

See also=其他参考=

• Atmospheric reanalysis
• General circulation model
• Atmospheric Radiation Measurement (ARM) (in the US)
• Climateprediction.net
• GFDL CM2.X
• GO-ESSP
• Numerical Weather Prediction
• Static atmospheric model
• Tropical cyclone prediction model
• Verification and validation of computer simulation models
• CICE sea ice model
• 大气重新分析
• 大气环流模式
• 大气辐射测量(ARM)(美国)
• 气候预测网站
• 地球物理流体动力学实验室GFDL cm2. x Geophysical Fluid Dynamics Laboratory
• GO-ESSP
• 数值天气预报
• 静态大气模式
• 热带气旋预报模式
• 验证及确认计算机模拟模式
• CICE 海冰模式

Climate models on the web= 网上的气候模式 =

• Dapper/DChart — plot and download model data referenced by the Fourth Assessment Report (AR4) of the Intergovernmental Panel on Climate Change. (No longer available)
• NCAR/UCAR Community Climate System Model (CCSM)
• Do it yourself climate prediction
• Primary research GCM developed by NASA/GISS (Goddard Institute for Space Studies)
• Original NASA/GISS global climate model (GCM) with a user-friendly interface for PCs and Macs
• CCCma model info and interface to retrieve model data
• NOAA/Geophysical Fluid Dynamics Laboratory CM2 global climate model info and model output data files
• Dry idealized AGCM based on above GFDL CM2
• Model of an idealized Moist Atmosphere (MiMA): based on GFDL CM2. Complexity in-between dry models and full GCMs
• University of Victoria Global climate model, free for download. Leading researcher was a contributing author to an IPCC report on climate change.
• vimeo.com/user12523377/videos Visualizations of climate models of ETH Zurich
• Empirical Climate Model -{zh-cn:互联网档案馆; zh-tw:網際網路檔案館; zh-hk:互聯網檔案館;}-的存檔，存档日期24 March 2019.
• Dapper/DChart ー绘制和下载政府间气候变化专门委员会第四次评估报告(AR4)所引用的模式数据。原始的 NASA/GISS 全球气候模式(GCM) ，具有 pc 和 Macs 的用户友好界面
• CCCma 模式信息和用于检索模式数据的界面
• NOAA/地球物理流体动力学实验室 cm2全球气候模式信息和模式输出数据文件
• 基于上述 GFDL CM2M 的干式理想化 AGCM。Jucker，s. Fueglistaler 和 g. k. Vallis“在理想的 GCM 中平流层突然变暖”。地球物理研究期刊: 大气2014119(19)11,054-11,064;
• 理想化潮湿大气模型: 基于 GFDL CM2。复杂度介于干燥模型和完全 GCMsM 之间。Jucker 和 E.p. Gerber: “用理想的湿模式解析热带对流层顶层的年循环”。气候杂志201730(18-rrb- 7339-7358;
• 维多利亚大学全球气候模型，免费下载。首席研究员是 IPCC 气候变化报告的特约作者。
• 苏黎世联邦理工学院气候模型的 vimeo.com/user12523377/videos 可视化
• 经验气候模型

Bibliography

• Roulstone, Ian; Norbury, John (2013). [[[:模板:Google books]] Invisible in the Storm: the role of mathematics in understanding weather]. Princeton University Press. 模板:Google books. 

External links= 外部链接 =

• Coupled Model Intercomparison Project
• On the Radiative and Dynamical Feedbacks over the Equatorial Pacific Cold Tongue
• Basic Radiation Calculations — The Discovery of Global Warming
• Henderson-Sellers, A.; Robinson, P. J. (1999). Contemporary Climatology. New York: Longman. ISBN 978-0-582-27631-4. http://www.pearsoned.co.uk/Bookshop/detail.asp?item=100000000002249. 
• Climate Modeling 101 website by the U.S. National Research Council — This site is a primer on how climate models work. The information is based on expert, consensus reports from the U.S. National Research Council's Board on Atmospheric Sciences and Climate. The most recent is A National Strategy for Advancing Climate Modeling -{zh-cn:互联网档案馆; zh-tw:網際網路檔案館; zh-hk:互聯網檔案館;}-的存檔，存档日期3 October 2012..
• Why results from the next generation of climate models matter CarbonBrief, Guest post by Belcher, Boucher, Sutton, 21 March 2019
• Builder Insight - Modelling the Future Climate in Passively Cooled Buildings
• 耦合模式相互比较项目
• 赤道太平洋冷舌上空的辐射和动力反馈
• 基本辐射计算ー全球变暖的发现
• 美国国家研究委员会气候模式101网站ー这个网站是气候模式如何工作的入门。这些信息是基于美国国家研究委员会大气科学和气候委员会的专家共识报告。最近的一份是《推进气候模拟的国家战略》。
• 为何下一代气候模型的结果与 CarbonBrief 有关? Belcher，Boucher，Sutton，2019年3月21日

Category:Numerical climate and weather models

类别: 数值气候和天气模型

This page was moved from wikipedia:en:Climate model. Its edit history can be viewed at 气候模式/edithistory