霍奇金-赫胥黎模型

此词条由神经动力学读书会词条梳理志愿者安贞桦翻译审校，未经专家审核，带来阅读不便，请见谅。

Basic components of Hodgkin–Huxley-type models. Hodgkin–Huxley type models represent the biophysical characteristic of cell membranes. The lipid bilayer is represented as a capacitance (C_m). Voltage-gated and leak ion channels are represented by nonlinear (g_n) and linear (g_L) conductances, respectively. The electrochemical gradients driving the flow of ions are represented by batteries (E), and ion pumps and exchangers are represented by current sources (I_p).

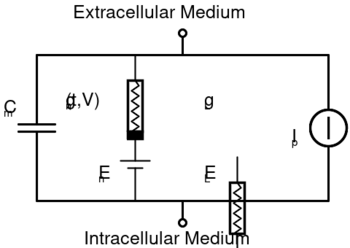
thumb|right|350px|Basic components of Hodgkin–Huxley-type models. Hodgkin–Huxley type models represent the biophysical characteristic of cell membranes. The lipid bilayer is represented as a capacitance (C_m). Voltage-gated and leak ion channels are represented by nonlinear (g_n) and linear (g_L) conductances, respectively. The electrochemical gradients driving the flow of ions are represented by batteries (E), and ion pumps and exchangers are represented by current sources (I_p).

拇指 | 右侧 | 350px | Hodgkin-huxley 型模型的基本组件。Hodgkin-Huxley 型模型代表了细胞膜的生物物理特性。脂双分子层表示为电容(c < sub > m )。电压门控离子通道和泄漏离子通道分别用非线性(g < sub > n )和线性(g < sub > l )电导表示。驱动离子流的电化学梯度用电池(e)表示，离子泵和离子交换器用电流源表示(i < sub > p )。

The Hodgkin–Huxley model, or conductance-based model, is a mathematical model that describes how action potentials in neurons are initiated and propagated. It is a set of nonlinear differential equations that approximates the electrical characteristics of excitable cells such as neurons and cardiac myocytes. It is a continuous-time dynamical system.

The Hodgkin–Huxley model, or conductance-based model, is a mathematical model that describes how action potentials in neurons are initiated and propagated. It is a set of nonlinear differential equations that approximates the electrical characteristics of excitable cells such as neurons and cardiac myocytes. It is a continuous-time dynamical system.

Hodgkin-Huxley 模型，或者说基于电导的模型，是一个描述神经元中动作电位如何发生和传播的数学模型。它是一组非线性微分方程，近似于神经元和心肌细胞等可兴奋细胞的电学特性。它是一个连续的时间动力系统。

Alan Hodgkin and Andrew Huxley described the model in 1952 to explain the ionic mechanisms underlying the initiation and propagation of action potentials in the squid giant axon. They received the 1963 Nobel Prize in Physiology or Medicine for this work.

Alan Hodgkin and Andrew Huxley described the model in 1952 to explain the ionic mechanisms underlying the initiation and propagation of action potentials in the squid giant axon. They received the 1963 Nobel Prize in Physiology or Medicine for this work.

1952年，Alan Hodgkin 和 Andrew Huxley 描述了这个模型，以解释乌贼巨大神经轴动作电位启动和传播的离子机制。他们因为这项工作获得了1963年的诺贝尔生理学或医学奖。

Basic components

The typical Hodgkin–Huxley model treats each component of an excitable cell as an electrical element (as shown in the figure). The lipid bilayer is represented as a capacitance (C_m). Voltage-gated ion channels are represented by electrical conductances (g_n, where n is the specific ion channel) that depend on both voltage and time. Leak channels are represented by linear conductances (g_L). The electrochemical gradients driving the flow of ions are represented by voltage sources (E_n) whose voltages are determined by the ratio of the intra- and extracellular concentrations of the ionic species of interest. Finally, ion pumps are represented by current sources (I_p).模板:Clarify The membrane potential is denoted by V_m.

The typical Hodgkin–Huxley model treats each component of an excitable cell as an electrical element (as shown in the figure). The lipid bilayer is represented as a capacitance (C_m). Voltage-gated ion channels are represented by electrical conductances (g_n, where n is the specific ion channel) that depend on both voltage and time. Leak channels are represented by linear conductances (g_L). The electrochemical gradients driving the flow of ions are represented by voltage sources (E_n) whose voltages are determined by the ratio of the intra- and extracellular concentrations of the ionic species of interest. Finally, ion pumps are represented by current sources (I_p). The membrane potential is denoted by V_m.

= = 基本成分 = = 典型的 Hodgkin-Huxley 模型将可兴奋细胞的每个成分都当作电子元件来处理(如图所示)。脂双分子层表示为电容(c < sub > m )。电压门控离子通道由电导表示(g < sub > n ，其中 n 是特定的离子通道) ，它同时依赖于电压和时间。泄漏通道用线性电导表示(g < sub > l )。驱动离子流的电化学梯度由电压源(e < sub > n )表示，电压源的电压取决于相关离子种类的细胞内和细胞外浓度的比值。最后，用电流源表示离子泵(i < sub > p )。膜电位表示 v < sub > m 。

Mathematically, the current flowing through the lipid bilayer is written as

Mathematically, the current flowing through the lipid bilayer is written as

数学上，流过脂双分子层的电流被写成

[math]\displaystyle{ I_c = C_m\frac{{\mathrm d} V_m}{{\mathrm d} t} }[/math]

I_c = C_m\frac{{\mathrm d} V_m}{{\mathrm d} t}

i c = c m frac { mathrm d } v m }{ mathrm d } t

and the current through a given ion channel is the product

and the current through a given ion channel is the product

通过给定离子通道的电流

[math]\displaystyle{ I_i = {g_i}(V_m - V_i) \; }[/math]

I_i = {g_i}(V_m - V_i) \;

i i = { g _ i }(v _ m-v _ i) ;

where [math]\displaystyle{ V_i }[/math] is the reversal potential of the i-th ion channel. Thus, for a cell with sodium and potassium channels, the total current through the membrane is given by:

where V_i is the reversal potential of the i-th ion channel. Thus, for a cell with sodium and potassium channels, the total current through the membrane is given by:

其中 v _ i 是 i-th 离子通道的翻转电位。因此，对于具有钠和钾离子通道的细胞，通过细胞膜的总电流是:

[math]\displaystyle{ I = C_m\frac{{\mathrm d} V_m}{{\mathrm d} t} + g_K(V_m - V_K) + g_{Na}(V_m - V_{Na}) + g_l(V_m - V_l) }[/math]

where I is the total membrane current per unit area, C_m is the membrane capacitance per unit area, g_K and g_Na are the potassium and sodium conductances per unit area, respectively, V_K and V_Na are the potassium and sodium reversal potentials, respectively, and g_l and V_l are the leak conductance per unit area and leak reversal potential, respectively. The time dependent elements of this equation are V_m, g_Na, and g_K, where the last two conductances depend explicitly on voltage as well.

I = C_m\frac{{\mathrm d} V_m}{{\mathrm d} t} + g_K(V_m - V_K) + g_{Na}(V_m - V_{Na}) + g_l(V_m - V_l)

where I is the total membrane current per unit area, Cm is the membrane capacitance per unit area, gK and gNa are the potassium and sodium conductances per unit area, respectively, VK and VNa are the potassium and sodium reversal potentials, respectively, and gl and Vl are the leak conductance per unit area and leak reversal potential, respectively. The time dependent elements of this equation are Vm, gNa, and gK, where the last two conductances depend explicitly on voltage as well.

i = c _ m frac { mathrm d } v _ m }{ mathrm d } t } + g _ k (v _ m-v _ k) + g _ Na }(v _ m-v _ Na }) + g _ l (v _ m-v _ v _ l)其中 i 为单位面积的总膜电流，Cm 为单位面积的膜电流，gK 和 gNa 为单位面积的钾和钠电容，VK 和 VNa 分别为钾电容和反转电势，钠电容和 Vl 分别为单位面积的渗漏和翻转电位。这个方程中与时间有关的元素是 Vm、 gNa 和 gK，其中最后两个电导也明确地依赖于电压。

= 离子电流角色塑造 =

In voltage-gated ion channels, the channel conductance [math]\displaystyle{ g_l }[/math] is a function of both time and voltage ([math]\displaystyle{ g_n(t,V) }[/math] in the figure), while in leak channels [math]\displaystyle{ g_l }[/math] is a constant ([math]\displaystyle{ g_L }[/math] in the figure). The current generated by ion pumps is dependent on the ionic species specific to that pump. The following sections will describe these formulations in more detail.

In voltage-gated ion channels, the channel conductance g_l is a function of both time and voltage (g_n(t,V) in the figure), while in leak channels g_l is a constant (g_L in the figure). The current generated by ion pumps is dependent on the ionic species specific to that pump. The following sections will describe these formulations in more detail.

在电压门控离子通道中，沟道电导 g _ l 是时间和电压(图中为 g _ n (t，v))的函数，而在泄漏通道中，g _ l 是常数(图中为 g _ l)。离子泵产生的电流取决于离子泵特有的离子种类。以下各节将更详细地描述这些公式。

Voltage-gated ion channels

Using a series of voltage clamp experiments and by varying extracellular sodium and potassium concentrations, Hodgkin and Huxley developed a model in which the properties of an excitable cell are described by a set of four ordinary differential equations. Together with the equation for the total current mentioned above, these are:

Using a series of voltage clamp experiments and by varying extracellular sodium and potassium concentrations, Hodgkin and Huxley developed a model in which the properties of an excitable cell are described by a set of four ordinary differential equations. Together with the equation for the total current mentioned above, these are:

通过一系列的电压钳实验，通过改变细胞外钠离子和钾离子浓度，Hodgkin 和 Huxley 建立了一个由四个常微分方程描述兴奋细胞特性的模型。加上上述总电流的等式，这些是:

[math]\displaystyle{ I = C_m\frac{{\mathrm d} V_m}{{\mathrm d} t} + \bar{g}_\text{K}n^4(V_m - V_K) + \bar{g}_\text{Na}m^3h(V_m - V_{Na}) + \bar{g}_l(V_m - V_l), }[/math]

I = C_m\frac{{\mathrm d} V_m}{{\mathrm d} t} + \bar{g}_\text{K}n^4(V_m - V_K) + \bar{g}_\text{Na}m^3h(V_m - V_{Na}) + \bar{g}_l(V_m - V_l),

i = c _ m frac { mathrm d } v _ m }{{ mathrm d } t } + bar { g } text { k } n ^ 4(v _ m-v _ k) + bar { g }文本{ Na } m ^ 3 h (v _ m-v _ Na }) + bar { g } l (v _ m-v _ l) ,

[math]\displaystyle{ \frac{dn}{dt} = \alpha_n(V_m)(1 - n) - \beta_n(V_m) n }[/math]

\frac{dn}{dt} = \alpha_n(V_m)(1 - n) - \beta_n(V_m) n

frac { dn }{ dt } = alpha _ n (v _ m)(1-n)-beta _ n (v _ m) n

[math]\displaystyle{ \frac{dm}{dt} = \alpha_m(V_m)(1 - m) - \beta_m(V_m) m }[/math]

\frac{dm}{dt} = \alpha_m(V_m)(1 - m) - \beta_m(V_m) m

frac { dm }{ dt } = alpha _ m (v _ m)(1-m)-beta _ m (v _ m) m

[math]\displaystyle{ \frac{dh}{dt} = \alpha_h(V_m)(1 - h) - \beta_h(V_m) h }[/math]

\frac{dh}{dt} = \alpha_h(V_m)(1 - h) - \beta_h(V_m) h

frac { dh }{ dt } = alpha _ h (v _ m)(1-h)-beta _ h (v _ m) h

where I is the current per unit area, and [math]\displaystyle{ \alpha_i }[/math] and [math]\displaystyle{ \beta_i }[/math] are rate constants for the i-th ion channel, which depend on voltage but not time. [math]\displaystyle{ \bar{g}_n }[/math] is the maximal value of the conductance. n, m, and h are dimensionless quantities between 0 and 1 that are associated with potassium channel activation, sodium channel activation, and sodium channel inactivation, respectively. For [math]\displaystyle{ p = (n, m, h) }[/math], [math]\displaystyle{ \alpha_p }[/math] and [math]\displaystyle{ \beta_p }[/math] take the form

where I is the current per unit area, and \alpha_i and \beta_i are rate constants for the i-th ion channel, which depend on voltage but not time. \bar{g}_n is the maximal value of the conductance. n, m, and h are dimensionless quantities between 0 and 1 that are associated with potassium channel activation, sodium channel activation, and sodium channel inactivation, respectively. For p = (n, m, h), \alpha_p and \beta_p take the form

其中 i 是单位面积的电流，而 alpha _ i 和 beta _ i 是 i-th 离子通道的速率常数，它取决于电压而不是时间。巴{ g } _ n 是电导的最大值。N、 m 和 h 是0和1之间的无量纲量，分别与钾离子通道激活、钠通道激活和钠通道失活有关。对于 p = (n，m，h) ，alpha _ p 和 beta _ p 的形式是

[math]\displaystyle{ \alpha_p(V_m) = p_\infty(V_m)/\tau_p }[/math]

\alpha_p(V_m) = p_\infty(V_m)/\tau_p

alpha _ p (v _ m) = p _ infty (v _ m)/tau _ p

[math]\displaystyle{ \beta_p(V_m) = (1 - p_\infty(V_m))/\tau_p. }[/math]

\beta_p(V_m) = (1 - p_\infty(V_m))/\tau_p.

beta _ p (v _ m) = (1-p _ infty (v _ m))/tau _ p.

[math]\displaystyle{ p_\infty }[/math] and [math]\displaystyle{ (1-p_\infty) }[/math] are the steady state values for activation and inactivation, respectively, and are usually represented by Boltzmann equations as functions of [math]\displaystyle{ V_m }[/math]. In the original paper by Hodgkin and Huxley, the functions [math]\displaystyle{ \alpha }[/math] and [math]\displaystyle{ \beta }[/math] are given by

[math]\displaystyle{ \begin{array}{lll} \alpha_n(V_m) = \frac{0.01(10-V)}{\exp\big(\frac{10-V}{10}\big)-1} & \alpha_m(V_m) = \frac{0.1(25-V)}{\exp\big(\frac{25-V}{10}\big)-1} & \alpha_h(V_m) = 0.07\exp\bigg(-\frac{V}{20}\bigg)\\ \beta_n(V_m) = 0.125\exp\bigg(-\frac{V}{80}\bigg) & \beta_m(V_m) = 4\exp\bigg(-\frac{V}{18}\bigg) & \beta_h(V_m) = \frac{1}{\exp\big(\frac{30-V}{10}\big) + 1} \end{array} }[/math]

where [math]\displaystyle{ V = V_{rest} - V_m }[/math] denotes the negative depolarization in mV.

p_\infty and (1-p_\infty) are the steady state values for activation and inactivation, respectively, and are usually represented by Boltzmann equations as functions of V_m. In the original paper by Hodgkin and Huxley, the functions \alpha and \beta are given by

\begin{array}{lll}

\alpha_n(V_m) = \frac{0.01(10-V)}{\exp\big(\frac{10-V}{10}\big)-1} & \alpha_m(V_m) = \frac{0.1(25-V)}{\exp\big(\frac{25-V}{10}\big)-1} & \alpha_h(V_m) = 0.07\exp\bigg(-\frac{V}{20}\bigg)\\

\beta_n(V_m) = 0.125\exp\bigg(-\frac{V}{80}\bigg) & \beta_m(V_m) = 4\exp\bigg(-\frac{V}{18}\bigg) & \beta_h(V_m) = \frac{1}{\exp\big(\frac{30-V}{10}\big) + 1} \end{array} where V = V_{rest} - V_m denotes the negative depolarization in mV.

P _ infty 和(1-p _ infty)分别是活化和失活的稳态值，通常用 Boltzmann 方程表示为 v _ m 的函数。在 Hodgkin 和 Huxley 的原始论文中，给出了函数 alpha 和 beta: begin { array }{ lll } alpha _ n (v _ m) = frac {0.01(10-V)}{ exp big (frac {10-V }{10} big)-1} & alpha _ m (v _ m) = frac {0.1(25-V)}{ exp big (frac {25-V }{10} big)-1} & alpha _ h (v _ m) = 0.07 expBigg (- frac { v } bigg) beta _ n (v _ m) = 0.125 exp bigg (- frac { v } bigg) & beta _ m (v _ m) = 4 exp bigg (- frac { v }{18} bigg) & beta _ h ()V _ m) = frac {1}{ exp big (frac {30-V }{10} big) + 1} end { array }其中 v = v _ { rest }{ rest }-v _ m 表示 mV 中的负去极化。

While in many current software programs, Hodgkin–Huxley type models generalize [math]\displaystyle{ \alpha }[/math] and [math]\displaystyle{ \beta }[/math] to

While in many current software programs,Nelson ME (2005) Electrophysiological Models In: Databasing the Brain: From Data to Knowledge. (S. Koslow and S. Subramaniam, eds.) Wiley, New York, pp. 285–301 Hodgkin–Huxley type models generalize \alpha and \beta to

虽然在许多当前的软件程序，尼尔森我(2005年)电生理模型在: 数据库的大脑: 从数据到知识。(s. Koslow and s. Subramaniam，eds.)威利，纽约，pp。285-301 Hodgkin-Huxley 型模型将 alpha 和 beta 推广到

[math]\displaystyle{ \frac{A_p(V_m-B_p)}{\exp\big(\frac{V_m-B_p}{C_p}\big)-D_p} }[/math]

\frac{A_p(V_m-B_p)}{\exp\big(\frac{V_m-B_p}{C_p}\big)-D_p}

frac { a _ p (v _ m-b _ p)}{ exp big (frac { v _ m-b _ p }{ c _ p } big)-d _ p }

In order to characterize voltage-gated channels, the equations are fit to voltage clamp data. For a derivation of the Hodgkin–Huxley equations under voltage-clamp, see. Briefly, when the membrane potential is held at a constant value (i.e., voltage-clamp), for each value of the membrane potential the nonlinear gating equations reduce to equations of the form:

In order to characterize voltage-gated channels, the equations are fit to voltage clamp data. For a derivation of the Hodgkin–Huxley equations under voltage-clamp, see. Briefly, when the membrane potential is held at a constant value (i.e., voltage-clamp), for each value of the membrane potential the nonlinear gating equations reduce to equations of the form:

为了表征电压门控通道，该方程适合于电压钳位数据。关于电压箝位下 Hodgkin-Huxley 方程的推导，请参阅。简单地说，当膜电位保持在一个恒定的值(例如，电压钳)时，对于每个膜电位的值，非线性门控方程可以归结为以下形式的方程:

[math]\displaystyle{ m(t) = m_{0} - [ (m_{0}-m_{\infty})(1 - e^{-t/\tau_m})]\, }[/math]

m(t) = m_{0} - [ (m_{0}-m_{\infty})(1 - e^{-t/\tau_m})]\,

M (t) = m _ {0}-[(m _ {0}-m _ { infty })(1-e ^ {-t/tau _ m })] ,

[math]\displaystyle{ h(t) = h_{0} - [ (h_{0}-h_{\infty})(1 - e^{-t/\tau_h})]\, }[/math]

h(t) = h_{0} - [ (h_{0}-h_{\infty})(1 - e^{-t/\tau_h})]\,

h (t) = h _ {0}-[(h _ {0}-h _ { infty })(1-e ^ {-t/tau _ h })] ,

[math]\displaystyle{ n(t) = n_{0} - [ (n_{0}-n_{\infty})(1 - e^{-t/\tau_n})]\, }[/math]

n(t) = n_{0} - [ (n_{0}-n_{\infty})(1 - e^{-t/\tau_n})]\,

n (t) = n _ {0}-[(n _ {0}-n _ { infty })(1-e ^ {-t/tau _ n })] ,

Thus, for every value of membrane potential [math]\displaystyle{ V_{m} }[/math] the sodium and potassium currents can be described by

Thus, for every value of membrane potential V_{m} the sodium and potassium currents can be described by

因此，对于每一个膜电位 v { m }的值，钠电流和钾电流可以用以下方法来描述

[math]\displaystyle{ I_\mathrm{Na}(t)=\bar{g}_\mathrm{Na} m(V_m)^3h(V_m)(V_m-E_\mathrm{Na}), }[/math]

I_\mathrm{Na}(t)=\bar{g}_\mathrm{Na} m(V_m)^3h(V_m)(V_m-E_\mathrm{Na}),

i _ mathrm { Na }(t) = bar { g } _ mathrm { Na } m (v _ m) ^ 3h (v _ m)(v _ m-e _ mathrm { Na }) ,

[math]\displaystyle{ I_\mathrm{K}(t)=\bar{g}_\mathrm{K} n(V_m)^4(V_m-E_\mathrm{K}). }[/math]

I_\mathrm{K}(t)=\bar{g}_\mathrm{K} n(V_m)^4(V_m-E_\mathrm{K}).

i _ mathrm { k }(t) = bar { g } _ mathrm { k } n (v _ m) ^ 4(v _ m-e _ mathrm { k }).

In order to arrive at the complete solution for a propagated action potential, one must write the current term I on the left-hand side of the first differential equation in terms of V, so that the equation becomes an equation for voltage alone. The relation between I and V can be derived from cable theory and is given by

In order to arrive at the complete solution for a propagated action potential, one must write the current term I on the left-hand side of the first differential equation in terms of V, so that the equation becomes an equation for voltage alone. The relation between I and V can be derived from cable theory and is given by

为了得到传播的动作电位的完整解，必须在第一个微分方程的左侧写上电流项 i，使方程成为单独的电压方程。I 和 v 之间的关系可以从电缆理论中推导出来，并给出了

[math]\displaystyle{ I = \frac{a}{2R}\frac{\partial^2V}{\partial x^2}, }[/math]

I = \frac{a}{2R}\frac{\partial^2V}{\partial x^2},

2 r } frac { partial ^ 2V }{ partial x ^ 2} ,

where a is the radius of the axon, R is the specific resistance of the axoplasm, and x is the position along the nerve fiber. Substitution of this expression for I transforms the original set of equations into a set of partial differential equations, because the voltage becomes a function of both x and t.

where a is the radius of the axon, R is the specific resistance of the axoplasm, and x is the position along the nerve fiber. Substitution of this expression for I transforms the original set of equations into a set of partial differential equations, because the voltage becomes a function of both x and t.

其中 a 是轴突的半径，r 是轴浆的比阻力，x 是沿着神经纤维的位置。用这个表达式代替 i，将原来的方程组变换为一组偏微分方程，因为电压变成了 x 和 t 的函数。

The Levenberg–Marquardt algorithm is often used to fit these equations to voltage-clamp data.

The Levenberg–Marquardt algorithm is often used to fit these equations to voltage-clamp data.

通常采用 Levenberg-Marquardt 算法对电压钳位数据进行拟合。

While the original experiments treated only sodium and potassium channels, the Hodgkin–Huxley model can also be extended to account for other species of ion channels.

While the original experiments treated only sodium and potassium channels, the Hodgkin–Huxley model can also be extended to account for other species of ion channels.

虽然最初的实验只处理钠和钾离子通道，Hodgkin-Huxley 模型也可以扩展到其他种类的离子通道。

Leak channels

Leak channels account for the natural permeability of the membrane to ions and take the form of the equation for voltage-gated channels, where the conductance [math]\displaystyle{ g_{leak} }[/math] is a constant. Thus, the leak current due to passive leak ion channels in the Hodgkin-Huxley formalism is [math]\displaystyle{ I_l=g_{leak}(V-V_{leak}) }[/math].

Leak channels account for the natural permeability of the membrane to ions and take the form of the equation for voltage-gated channels, where the conductance g_{leak} is a constant. Thus, the leak current due to passive leak ion channels in the Hodgkin-Huxley formalism is I_l=g_{leak}(V-V_{leak}).

= = = 泄漏通道 = = = 泄漏通道解释了膜对离子的天然渗透性，其形式为电压门控通道方程，其中 g {泄漏}为常数。因此，在 Hodgkin-Huxley 公式中，被动泄漏离子通道引起的泄漏电流为 i _ l = g _ { leak }(V-V _ { leak })。

Pumps and exchangers

The membrane potential depends upon the maintenance of ionic concentration gradients across it. The maintenance of these concentration gradients requires active transport of ionic species. The sodium-potassium and sodium-calcium exchangers are the best known of these. Some of the basic properties of the Na/Ca exchanger have already been well-established: the stoichiometry of exchange is 3 Na⁺: 1 Ca²⁺ and the exchanger is electrogenic and voltage-sensitive. The Na/K exchanger has also been described in detail, with a 3 Na⁺: 2 K⁺ stoichiometry.

The membrane potential depends upon the maintenance of ionic concentration gradients across it. The maintenance of these concentration gradients requires active transport of ionic species. The sodium-potassium and sodium-calcium exchangers are the best known of these. Some of the basic properties of the Na/Ca exchanger have already been well-established: the stoichiometry of exchange is 3 Na⁺: 1 Ca²⁺ and the exchanger is electrogenic and voltage-sensitive. The Na/K exchanger has also been described in detail, with a 3 Na⁺: 2 K⁺ stoichiometry.

= = = 泵和交换器 = = = 膜电位取决于维持其上的离子浓度梯度。维持这些浓度梯度需要离子种类的主动运输。其中钠钾交换器和钠钙交换器最为著名。钠钙交换器的一些基本性质已经得到确认: 交换的化学计量比为3 Na < sup > +  : 1 Ca < sup > 2 + ，交换器具有产电性和电压敏感性。本文还详细描述了 Na/k 交换剂，用3个 Na < sup > +  : 2 k < sup > + 化学计量学方法。

Mathematical properties

The Hodgkin–Huxley model can be thought of as a differential equation system with four state variables, [math]\displaystyle{ V_m(t), n(t), m(t) }[/math], and [math]\displaystyle{ h(t) }[/math], that change with respect to time [math]\displaystyle{ t }[/math]. The system is difficult to study because it is a nonlinear system and cannot be solved analytically. However, there are many numerical methods available to analyze the system. Certain properties and general behaviors, such as limit cycles, can be proven to exist.

The Hodgkin–Huxley model can be thought of as a differential equation system with four state variables, V_m(t), n(t), m(t), and h(t), that change with respect to time t. The system is difficult to study because it is a nonlinear system and cannot be solved analytically. However, there are many numerical methods available to analyze the system. Certain properties and general behaviors, such as limit cycles, can be proven to exist.

= = = 数学性质 = = Hodgkin-Huxley 模型可以被认为是一个具有4个状态变量 v _ m (t) ，n (t) ，m (t)和 h (t)的微分方程系统，它们随着时间 t 的变化而变化。这个系统很难研究，因为它是一个非线性，无法用解析方法求解。然而，有许多数值方法可用于分析该系统。某些性质和一般行为，如极限环，可以被证明是存在的。

A simulation of the Hodgkin–Huxley model in phase space, in terms of voltage v(t) and potassium gating variable n(t). The closed curve is known as a limit cycle.

= 中心流形 =

Because there are four state variables, visualizing the path in phase space can be difficult. Usually two variables are chosen, voltage [math]\displaystyle{ V_m(t) }[/math] and the potassium gating variable [math]\displaystyle{ n(t) }[/math], allowing one to visualize the limit cycle. However, one must be careful because this is an ad-hoc method of visualizing the 4-dimensional system. This does not prove the existence of the limit cycle.

Because there are four state variables, visualizing the path in phase space can be difficult. Usually two variables are chosen, voltage V_m(t) and the potassium gating variable n(t), allowing one to visualize the limit cycle. However, one must be careful because this is an ad-hoc method of visualizing the 4-dimensional system. This does not prove the existence of the limit cycle.

由于有四个状态变量，在相空间中路径的可视化可能是困难的。通常选择两个变量，电压 v _ m (t)和钾浇注变量 n (t) ，使人可以想象极限环。但是，一定要小心，因为这是一个四维系统可视化的特别方法。这并不能证明极限环的存在性。

A better projection can be constructed from a careful analysis of the Jacobian of the system, evaluated at the equilibrium point. Specifically, the eigenvalues of the Jacobian are indicative of the center manifold's existence. Likewise, the eigenvectors of the Jacobian reveal the center manifold's orientation. The Hodgkin–Huxley model has two negative eigenvalues and two complex eigenvalues with slightly positive real parts. The eigenvectors associated with the two negative eigenvalues will reduce to zero as time t increases. The remaining two complex eigenvectors define the center manifold. In other words, the 4-dimensional system collapses onto a 2-dimensional plane. Any solution starting off the center manifold will decay towards the center manifold. Furthermore, the limit cycle is contained on the center manifold.

A better projection can be constructed from a careful analysis of the Jacobian of the system, evaluated at the equilibrium point. Specifically, the eigenvalues of the Jacobian are indicative of the center manifold's existence. Likewise, the eigenvectors of the Jacobian reveal the center manifold's orientation. The Hodgkin–Huxley model has two negative eigenvalues and two complex eigenvalues with slightly positive real parts. The eigenvectors associated with the two negative eigenvalues will reduce to zero as time t increases. The remaining two complex eigenvectors define the center manifold. In other words, the 4-dimensional system collapses onto a 2-dimensional plane. Any solution starting off the center manifold will decay towards the center manifold. Furthermore, the limit cycle is contained on the center manifold.

通过对系统的雅可比矩阵的仔细分析，可以构造出一个更好的投影，该投影在平衡点进行了评估。具体来说，特征值的雅可比是指示中心流形的存在。同样，雅可比的特征向量揭示了中心流形的方向。Hodgkin-Huxley 模型有两个负的特征值和两个带有轻微正实部的复特征值。随着时间 t 的增加，与两个负特征值相关的特征向量将减少到零。剩下的两个复特征向量定义了中心流形。换句话说，这个四维系统坍缩到一个二维平面上。任何解决方案开始的中心歧管将衰减到中心歧管。此外，极限环包含在中心流形上。

The voltage v(t) (in millivolts) of the Hodgkin–Huxley model, graphed over 50 milliseconds. The injected current varies from −5 nanoamps to 12 nanoamps. The graph passes through three stages: an equilibrium stage, a single-spike stage, and a limit cycle stage.

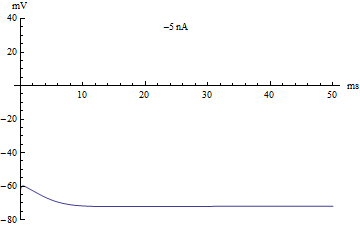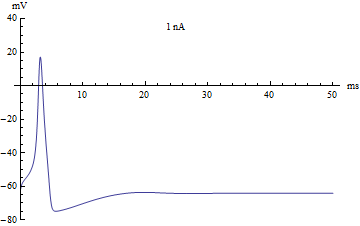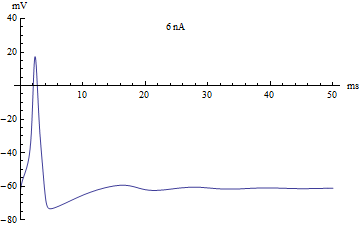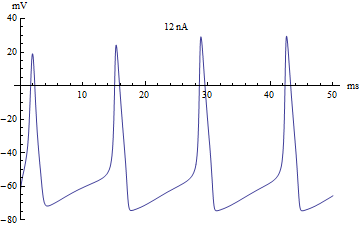
thumb|right|360px|The voltage v(t) (in millivolts) of the Hodgkin–Huxley model, graphed over 50 milliseconds. The injected current varies from −5 nanoamps to 12 nanoamps. The graph passes through three stages: an equilibrium stage, a single-spike stage, and a limit cycle stage.

拇指 | 右 | 360px | Hodgkin-Huxley 模型的电压 v (t)(毫伏) ，用图表表示超过50毫秒。注入电流从 -5纳安到12纳安不等。该图经历了三个阶段: 平衡阶段、单穗阶段和极限环阶段。

Bifurcations

If the injected current [math]\displaystyle{ I }[/math] were used as a bifurcation parameter, then the Hodgkin–Huxley model undergoes a Hopf bifurcation. As with most neuronal models, increasing the injected current will increase the firing rate of the neuron. One consequence of the Hopf bifurcation is that there is a minimum firing rate. This means that either the neuron is not firing at all (corresponding to zero frequency), or firing at the minimum firing rate. Because of the all-or-none principle, there is no smooth increase in action potential amplitude, but rather there is a sudden "jump" in amplitude. The resulting transition is known as a canard.

If the injected current I were used as a bifurcation parameter, then the Hodgkin–Huxley model undergoes a Hopf bifurcation. As with most neuronal models, increasing the injected current will increase the firing rate of the neuron. One consequence of the Hopf bifurcation is that there is a minimum firing rate. This means that either the neuron is not firing at all (corresponding to zero frequency), or firing at the minimum firing rate. Because of the all-or-none principle, there is no smooth increase in action potential amplitude, but rather there is a sudden "jump" in amplitude. The resulting transition is known as a canard.

如果将注入电流 i 作为分岔参数，那么 Hodgkin-Huxley 模型将经历一个霍普夫分岔。和大多数神经元模型一样，增加注入电流会增加神经元的放电频率。霍普夫分岔的一个结果就是有一个最低的开火率。这意味着要么神经元根本没有放电(对应于零频率) ，要么以最低放电速率放电。由于“全有或全无”原理，动作电位振幅的增加不是平稳的，而是突然的“跳跃”。由此产生的转变被称为谣言。

Improvements and alternative models

Main article: Biological neuron model

The Hodgkin–Huxley model is regarded as one of the great achievements of 20th-century biophysics. Nevertheless, modern Hodgkin–Huxley-type models have been extended in several important ways:

• Additional ion channel populations have been incorporated based on experimental data.
• The Hodgkin–Huxley model has been modified to incorporate transition state theory and produce thermodynamic Hodgkin–Huxley models.
• Models often incorporate highly complex geometries of dendrites and axons, often based on microscopy data.
• Stochastic models of ion-channel behavior, leading to stochastic hybrid systems.
• The Poisson–Nernst–Planck (PNP) model is based on a mean-field approximation of ion interactions and continuum descriptions of concentration and electrostatic potential.

The Hodgkin–Huxley model is regarded as one of the great achievements of 20th-century biophysics. Nevertheless, modern Hodgkin–Huxley-type models have been extended in several important ways:

• Additional ion channel populations have been incorporated based on experimental data.
• The Hodgkin–Huxley model has been modified to incorporate transition state theory and produce thermodynamic Hodgkin–Huxley models.
• Models often incorporate highly complex geometries of dendrites and axons, often based on microscopy data.
• Stochastic models of ion-channel behavior, leading to stochastic hybrid systems.
• The Poisson–Nernst–Planck (PNP) model is based on a mean-field approximation of ion interactions and continuum descriptions of concentration and electrostatic potential.

霍奇金-赫胥黎模型被认为是20世纪生物物理学的伟大成就之一。尽管如此，现代 Hodgkin-huxley 型模型已经在几个重要方面得到了扩展:

• 根据实验数据加入了额外的离子通道群。
• Hodgkin-Huxley 模型经过修正，纳入了过渡态理论，并产生了热力学 Hodgkin-Huxley 模型。
• 模型通常包含高度复杂的树突和轴突几何形状，通常基于显微镜数据。
• 离子通道行为的随机模型，导致随机混合系统。
• Poisson-Nernst-Planck 模型是基于离子相互作用的平均场近似以及浓度和静电势的连续描述。

Several simplified neuronal models have also been developed (such as the FitzHugh–Nagumo model), facilitating efficient large-scale simulation of groups of neurons, as well as mathematical insight into dynamics of action potential generation.

Several simplified neuronal models have also been developed (such as the FitzHugh–Nagumo model), facilitating efficient large-scale simulation of groups of neurons, as well as mathematical insight into dynamics of action potential generation.

一些简化的神经元模型(如 FitzHugh-Nagumo 模型)也已经被开发出来，它们有助于对神经元群进行有效的大规模模拟，以及对动作电位产生动力学的数学洞察。

See also

• Action potential
• Anode break excitation
• Autowave
• Biological neuron model
• Biological neural network
• FitzHugh–Nagumo model
• Galves–Löcherbach model
• GHK flux equation
• Goldman equation
• Memristor
• Neural accommodation
• Reaction–diffusion
• Theta model
• Rulkov map

• Action potential
• Anode break excitation
• Autowave
• Biological neuron model
• Biological neural network
• FitzHugh–Nagumo model
• Galves–Löcherbach model
• GHK flux equation
• Goldman equation
• Memristor
• Neural accommodation
• Reaction–diffusion
• Theta model
• Rulkov map

动作电位

• 阳极破坏激发
• 自波
• 生物神经元模型
• 生物神经网络
• FitzHugh-Nagumo 模型
• Galves-Löcherbach 模型
• GHK 通量方程
• 戈德曼方程
• 记忆电阻
• 反应扩散
• Theta 模型
• Rulkov 映射

= 进一步阅读 =

External links

• Interactive Javascript simulation of the HH model Runs in any HTML5 – capable browser. Allows for changing the parameters of the model and current injection.
• Interactive Java applet of the HH model Parameters of the model can be changed as well as excitation parameters and phase space plottings of all the variables is possible.
• Direct link to Hodgkin–Huxley model and a Description in BioModels Database
• Neural Impulses: The Action Potential In Action by Garrett Neske, The Wolfram Demonstrations Project
• Interactive Hodgkin–Huxley model by Shimon Marom, The Wolfram Demonstrations Project
• ModelDB A computational neuroscience source code database containing 4 versions (in different simulators) of the original Hodgkin–Huxley model and hundreds of models that apply the Hodgkin–Huxley model to other channels in many electrically excitable cell types.
• Several articles about the stochastic version of the model and its link with the original one.

• Interactive Javascript simulation of the HH model Runs in any HTML5 – capable browser. Allows for changing the parameters of the model and current injection.
• Interactive Java applet of the HH model Parameters of the model can be changed as well as excitation parameters and phase space plottings of all the variables is possible.
• Direct link to Hodgkin–Huxley model and a Description in BioModels Database
• Neural Impulses: The Action Potential In Action by Garrett Neske, The Wolfram Demonstrations Project
• Interactive Hodgkin–Huxley model by Shimon Marom, The Wolfram Demonstrations Project
• ModelDB A computational neuroscience source code database containing 4 versions (in different simulators) of the original Hodgkin–Huxley model and hundreds of models that apply the Hodgkin–Huxley model to other channels in many electrically excitable cell types.
• Several articles about the stochastic version of the model and its link with the original one.

= = = 外部链接 = =

• HH 模型的交互式 Javascript 模拟在任何支持 html5的浏览器中运行。允许更改模型和电流注入的参数。
• 交互式 Java 小程序的 HH 模型参数可以改变，以及所有变量的激励参数和相空间爆破是可能的。
• 直接链接到 Hodgkin-Huxley 模型和生物模型数据库的描述
• 神经冲动: 动作电位作者 Garrett Neske，Wolfram 演示项目
• 交互式 Hodgkin-Huxley 模型作者 Shimon Marom，Wolfram 演示项目模型 db a 计算神经科学源代码数据库包含原始 Hodgkin-Huxley 模型的4个版本(在不同的模拟器中)和数百个将 Hodgkin-Huxley 模型应用于许多电兴奋细胞类型的其他通道的模型。
• 关于模型的随机版本及其与原模型之间的联系的几篇文章。

Category:Nonlinear systems Category:Electrophysiology Category:Ion channels Category:Computational neuroscience

类别: 非线性系统类别: 电生理学类别: 离子通道类别: 计算神经科学

This page was moved from wikipedia:en:Hodgkin–Huxley model. Its edit history can be viewed at 霍奇金-赫胥黎模型/edithistory