霍奇金-赫胥黎模型

霍奇金-赫胥黎模型 Hodgkin-Huxley model,或者说基于电导的模型 conductance-based model,是一个描述神经元中动作电位如何产生和传导的数学模型。它是一组非线性微分方程,用于近似可兴奋细胞(如神经元和心肌细胞)的电学特性。它是一个时间连续的动力系统。
1952年,Alan Hodgkin和Andrew Huxley描述了这个模型,来解释乌贼巨轴突 squid giant axon中动作电位的产生和传导的离子机制。[1]他们因为这项工作获得了1963年的诺贝尔生理学或医学奖。
基本组成部分
经典的Hodgkin-Huxley模型将可兴奋细胞的每个部分都当作电路元件来处理(如图所示)。磷脂双分子层表示为电容([math]\displaystyle{ C_m }[/math])。电压门控离子通道表示为电导([math]\displaystyle{ g_n }[/math],其中n是特定的离子通道),它依赖于电压和时间。漏通道表示为线性电导([math]\displaystyle{ g_L }[/math])。驱使离子流动的电化学梯度表示为电压源([math]\displaystyle{ E_n }[/math]),电压源的电压取决于相关离子种类在细胞内和细胞外的浓度的比值。最后,离子泵表示为电流源([math]\displaystyle{ i_p }[/math])。膜电位表示为[math]\displaystyle{ V_m }[/math]。
数学上,流过磷脂双分子层的电流写为
- [math]\displaystyle{ I_c = C_m\frac{{\mathrm d} V_m}{{\mathrm d} t} }[/math]
流过给定离子通道的电流为乘积
- [math]\displaystyle{ I_i = {g_i}(V_m - V_i) \; }[/math]
其中 [math]\displaystyle{ V_i }[/math] 是第[math]\displaystyle{ i }[/math]个离子通道的反转电位。因此,对于具有钠和钾离子通道的细胞,通过细胞膜的总电流为:
- [math]\displaystyle{ I = C_m\frac{{\mathrm d} V_m}{{\mathrm d} t} + g_K(V_m - V_K) + g_{Na}(V_m - V_{Na}) + g_l(V_m - V_l) }[/math]
其中[math]\displaystyle{ I }[/math]为单位面积的总膜电流,[math]\displaystyle{ C_m }[/math]为单位面积的膜电容,[math]\displaystyle{ g_K }[/math]和[math]\displaystyle{ g_{Na} }[/math]分别为单位面积的钾和钠的电导,[math]\displaystyle{ V_K }[/math]和[math]\displaystyle{ V_{Na} }[/math]分别为钾和钠的反转电位,[math]\displaystyle{ g_l }[/math]和[math]\displaystyle{ V_l }[/math]分别为单位面积的漏电导和漏反转电位。这个方程中对时间依赖的项为[math]\displaystyle{ V_m }[/math]、[math]\displaystyle{ g_{Na} }[/math]和[math]\displaystyle{ g_K }[/math],其中最后两个电导项也明确地取决于电压。
离子电流的刻画
在电压门控离子通道中,通道电导[math]\displaystyle{ g_l }[/math]是时间和电压(图中为 [math]\displaystyle{ g_n(t,V) }[/math])的函数,而在漏通道中,[math]\displaystyle{ g_l }[/math]是常数(图中为[math]\displaystyle{ g_L }[/math])。由离子泵产生的电流取决于离子泵特定的离子种类。以下各节将更详细地描述这些公式。
电压门控离子通道
通过改变细胞外钠离子和钾离子的浓度,进行一系列的电压钳实验,Hodgkin和Huxley建立了一个由四个常微分方程描述的可兴奋细胞特性的模型。[1]加上上述总电流的方程,这些方程为:
- [math]\displaystyle{ I = C_m\frac{{\mathrm d} V_m}{{\mathrm d} t} + \bar{g}_\text{K}n^4(V_m - V_K) + \bar{g}_\text{Na}m^3h(V_m - V_{Na}) + \bar{g}_l(V_m - V_l), }[/math]
- [math]\displaystyle{ \frac{dn}{dt} = \alpha_n(V_m)(1 - n) - \beta_n(V_m) n }[/math]
- [math]\displaystyle{ \frac{dm}{dt} = \alpha_m(V_m)(1 - m) - \beta_m(V_m) m }[/math]
- [math]\displaystyle{ \frac{dh}{dt} = \alpha_h(V_m)(1 - h) - \beta_h(V_m) h }[/math]
其中[math]\displaystyle{ I }[/math]是单位面积的电流,而[math]\displaystyle{ \alpha_i }[/math]和[math]\displaystyle{ \beta_i }[/math]是第[math]\displaystyle{ i }[/math]个离子通道的速率常数,它取决于电压而非时间。[math]\displaystyle{ \bar{g}_n }[/math]是电导的最大值。[math]\displaystyle{ N }[/math]、[math]\displaystyle{ m }[/math]和[math]\displaystyle{ h }[/math]是0和1之间的无量纲量,分别与钾通道激活、钠通道激活和钠通道失活有关。对于[math]\displaystyle{ p = (n,m,h) }[/math],[math]\displaystyle{ \alpha_p }[/math]和[math]\displaystyle{ \beta_p }[/math]的形式是
- [math]\displaystyle{ \alpha_p(V_m) = p_\infty(V_m)/\tau_p }[/math]
- [math]\displaystyle{ \beta_p(V_m) = (1 - p_\infty(V_m))/\tau_p. }[/math]
[math]\displaystyle{ p_\infty }[/math]和[math]\displaystyle{ (1-p_\infty) }[/math]分别是激活和失活的稳态值,通常用玻尔兹曼方程表示为[math]\displaystyle{ V_m }[/math]的函数。
在Hodgkin和Huxley的原始论文[1]中,[math]\displaystyle{ \alpha }[/math]和[math]\displaystyle{ \beta }[/math]函数如下给出
- [math]\displaystyle{ \begin{array}{lll} \alpha_n(V_m) = \frac{0.01(10-V)}{\exp\big(\frac{10-V}{10}\big)-1} & \alpha_m(V_m) = \frac{0.1(25-V)}{\exp\big(\frac{25-V}{10}\big)-1} & \alpha_h(V_m) = 0.07\exp\bigg(-\frac{V}{20}\bigg)\\ \beta_n(V_m) = 0.125\exp\bigg(-\frac{V}{80}\bigg) & \beta_m(V_m) = 4\exp\bigg(-\frac{V}{18}\bigg) & \beta_h(V_m) = \frac{1}{\exp\big(\frac{30-V}{10}\big) + 1} \end{array} }[/math]
其中[math]\displaystyle{ V = V_{rest} - V_m }[/math]表示负去极化,单位为mV。
在当前的软件程序中[2],霍奇金-赫胥黎类模型将[math]\displaystyle{ \alpha }[/math]和[math]\displaystyle{ \beta }[/math]归纳为
- [math]\displaystyle{ \frac{A_p(V_m-B_p)}{\exp\big(\frac{V_m-B_p}{C_p}\big)-D_p} }[/math]
为了刻画电压门控通道,该方程拟合自电压钳数据。关于电压钳下Hodgkin-Huxley方程的推导,请参阅[3]。简单来说,当膜电位保持为一个恒定值(即电压钳取值)时,对于膜电位的每个值,非线性门控方程可以归结为以下形式的方程:
- [math]\displaystyle{ m(t) = m_{0} - [ (m_{0}-m_{\infty})(1 - e^{-t/\tau_m})]\, }[/math]
- [math]\displaystyle{ h(t) = h_{0} - [ (h_{0}-h_{\infty})(1 - e^{-t/\tau_h})]\, }[/math]
- [math]\displaystyle{ n(t) = n_{0} - [ (n_{0}-n_{\infty})(1 - e^{-t/\tau_n})]\, }[/math]
因此,对于膜电位的每个值[math]\displaystyle{ V_m }[/math],钠电流和钾电流可以描述为
- [math]\displaystyle{ I_\mathrm{Na}(t)=\bar{g}_\mathrm{Na} m(V_m)^3h(V_m)(V_m-E_\mathrm{Na}), }[/math]
- [math]\displaystyle{ I_\mathrm{K}(t)=\bar{g}_\mathrm{K} n(V_m)^4(V_m-E_\mathrm{K}). }[/math]
为了得到传导的动作电位的完全解,必须将第一个微分方程左侧的电流项 [math]\displaystyle{ I }[/math]写为[math]\displaystyle{ V }[/math]的形式,使方程成为单独的电压方程。[math]\displaystyle{ I }[/math]和[math]\displaystyle{ V }[/math]之间的关系可以从电缆理论中推导出来,即
- [math]\displaystyle{ I = \frac{a}{2R}\frac{\partial^2V}{\partial x^2}, }[/math]
其中[math]\displaystyle{ a }[/math]是轴突的半径,[math]\displaystyle{ R }[/math]是轴浆的比电阻,[math]\displaystyle{ x }[/math]是沿神经纤维的位置。用这个表达式代替[math]\displaystyle{ I }[/math],将原来的方程组转变为一组偏微分方程,因为电压变为[math]\displaystyle{ x }[/math]和[math]\displaystyle{ t }[/math]的函数。
通常采用Levenberg-Marquardt 算法通过电压钳数据拟合这些方程。[4]
虽然最初的实验只处理钠和钾通道,Hodgkin-Huxley模型也可以扩展到其他种类的离子通道。
漏通道
漏通道解释了膜对离子的天然渗透性,其形式为电压门控通道方程,其中电导[math]\displaystyle{ g_{leak} }[/math]为常数。因此,在Hodgkin-Huxley公式中,被动漏离子通道引起的漏电流为[math]\displaystyle{ I_l=g_{leak}(V-V_{leak}) }[/math]。
泵和交换器
膜电位取决于其跨膜离子浓度梯度的保持。维持这些浓度梯度需要这几种离子的主动运输。其中钠钾交换器和钠钙交换器最为著名。钠钙交换器的一些基本性质已得到公认:交换的化学计量比为 3 Na+: 1 Ca2+,且具有生电性和电压敏感性。文献中还详细描述了Na/K交换器,它具有 3 Na+: 2 K+的化学计量比。[5][6]
数学性质
可以认为Hodgkin-Huxley模型是一个具有4个状态变量[math]\displaystyle{ V_m(t),n(t),m(t) }[/math],和[math]\displaystyle{ h(t) }[/math]的微分方程系统,它们随着时间[math]\displaystyle{ t }[/math]变化。这个系统很难研究,因为它是一个非线性系统,无法用解析法求解。然而,可以用许多数值方法分析该系统。可以证明某些性质和一般行为(如极限环)是存在的。

中心流形
由于有四个状态变量,想象相空间中的路径会比较困难。通常选择两个变量,电压[math]\displaystyle{ V_m(t) }[/math]和钾门控变量[math]\displaystyle{ n(t) }[/math],这样就能想象出极限环。但是,要注意这只是一个想象四维系统的特殊方法,并不能证明极限环的存在性。
在系统的平衡点处对雅可比矩阵仔细分析,可以构造出一个更好的投影。具体来说,雅可比矩阵的特征值指示中心流形的存在。同样,雅可比的特征向量揭示了中心流形的方向。Hodgkin-Huxley模型有两个负的特征值和两个具有轻微取正的实部的复特征值。随着时间t的增加,与两个负特征值相关的特征向量将减少到零。剩下的两个复特征向量定义了中心流形。换句话说,这个四维系统会坍缩到一个二维平面上。任何开始于中心流形的解将衰减至中心流形。Any solution starting off the center manifold will decay towards the center manifold.此外,极限环包含在中心流形上。
分岔
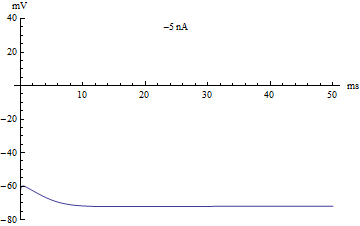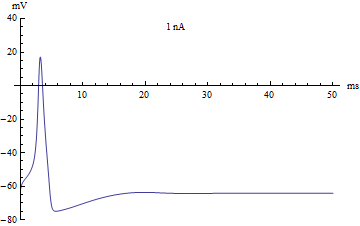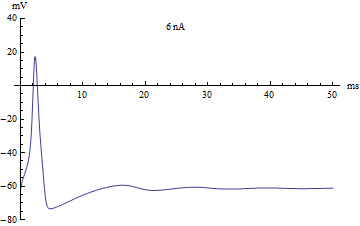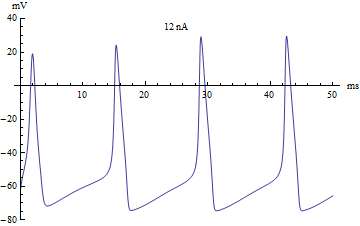
如果将注入电流[math]\displaystyle{ I }[/math]作为分岔参数,那么Hodgkin-Huxley模型将经历一个霍普夫分岔。和大多数神经元模型一样,增加注入电流会增加神经元的发放率。霍普夫分岔的一个结果就是存在一个最低的发放率。这意味着神经元要么根本没有发放(对应于零频率),要么以最低发放率放电。由于全或无原理,动作电位的幅度不存在平稳的增加,而是幅度上的突然“跳跃”。由此产生的转变被称为鸭解。
改进与可替代模型
Hodgkin-Huxley模型被认为是20世纪生物物理学的伟大成就之一。尽管如此,现代Hodgkin-Huxley型模型已经在几个重要方面得到了扩展:
- 根据实验数据引入了额外的离子通道群。
- 对Hodgkin-Huxley 模型加以修正,加入了过渡态理论,并产生了热力学Hodgkin-Huxley模型。[7]
- 通常基于显微镜数据,模型通常包含树突和轴突的高度复杂的几何形状。
- 离子通道行为的随机模型,导致随机混合系统。[8]
- Poisson-Nernst-Planck 模型是基于离子相互作用的平均场近似以及浓度和静电势的连续描述建立的。[9]
一些简化的神经元模型(如FitzHugh-Nagumo模型)也发展了出来,它们有助于对神经元群进行高效的大规模模拟,以及对动作电位产生的动力学的数学洞察。
参见
参考文献
- ↑ 1.0 1.1 1.2 Hodgkin AL, Huxley AF (August 1952). "A quantitative description of membrane current and its application to conduction and excitation in nerve". The Journal of Physiology. 117 (4): 500–44. doi:10.1113/jphysiol.1952.sp004764. PMC 1392413. PMID 12991237.
- ↑ Nelson ME (2005) Electrophysiological Models In: Databasing the Brain: From Data to Knowledge. (S. Koslow and S. Subramaniam, eds.) Wiley, New York, pp. 285–301
- ↑ Gray, Daniel Johnston; Wu, Samuel Miao-Sin (1997). Foundations of cellular neurophysiology (3rd ed.). Cambridge, Massachusetts [u.a.]: MIT Press. ISBN 978-0-262-10053-3.
- ↑ Krapivin, Vladimir F.; Varotsos, Costas A.; Soldatov, Vladimir Yu. (2015). New Ecoinformatics Tools in Environmental Science : Applications and Decision-making. Springer. pp. 37–38. ISBN 9783319139784. https://www.google.com/books/edition/New_Ecoinformatics_Tools_in_Environmenta/bWpnBgAAQBAJ?hl=en&gbpv=1&pg=PA37.
- ↑ Rakowski RF, Gadsby DC, De Weer P (May 1989). "Stoichiometry and voltage dependence of the sodium pump in voltage-clamped, internally dialyzed squid giant axon". The Journal of General Physiology. 93 (5): 903–41. doi:10.1085/jgp.93.5.903. PMC 2216238. PMID 2544655.
- ↑ Hille, Bertil (2001). Ion channels of excitable membranes (3rd ed.). Sunderland, Massachusetts: Sinauer. ISBN 978-0-87893-321-1.
- ↑ Forrest, M. D. (May 2014). "Can the Thermodynamic Hodgkin–Huxley Model of Voltage-Dependent Conductance Extrapolate for Temperature?" (PDF). Computation. 2 (2): 47–60. doi:10.3390/computation2020047.
- ↑ Pakdaman, K.; Thieullen, M.; Wainrib, G. (2010). "Fluid limit theorems for stochastic hybrid systems with applications to neuron models". Adv. Appl. Probab. 42 (3): 761–794. arXiv:1001.2474. Bibcode:2010arXiv1001.2474P. doi:10.1239/aap/1282924062. S2CID 18894661.
- ↑ Zheng, Q.; Wei, G. W. (May 2011). "Poisson-Boltzmann-Nernst-Planck model". Journal of Chemical Physics. 134 (19): 194101. Bibcode:2011JChPh.134s4101Z. doi:10.1063/1.3581031. PMC 3122111. PMID 21599038.
进一步阅读
- Hodgkin AL, Huxley AF (April 1952). "Currents carried by sodium and potassium ions through the membrane of the giant axon of Loligo". The Journal of Physiology. 116 (4): 449–72. doi:10.1113/jphysiol.1952.sp004717. PMC 1392213. PMID 14946713.
- Hodgkin AL, Huxley AF (April 1952). "The components of membrane conductance in the giant axon of Loligo". The Journal of Physiology. 116 (4): 473–96. doi:10.1113/jphysiol.1952.sp004718. PMC 1392209. PMID 14946714.
- Hodgkin AL, Huxley AF (April 1952). "The dual effect of membrane potential on sodium conductance in the giant axon of Loligo". The Journal of Physiology. 116 (4): 497–506. doi:10.1113/jphysiol.1952.sp004719. PMC 1392212. PMID 14946715.
- Hodgkin AL, Huxley AF (August 1952). "A quantitative description of membrane current and its application to conduction and excitation in nerve". The Journal of Physiology. 117 (4): 500–44. doi:10.1113/jphysiol.1952.sp004764. PMC 1392413. PMID 12991237.
- Hodgkin AL, Huxley AF, Katz B (April 1952). "Measurement of current-voltage relations in the membrane of the giant axon of Loligo". The Journal of Physiology. 116 (4): 424–48. doi:10.1113/jphysiol.1952.sp004716. PMC 1392219. PMID 14946712.
外部链接
- Interactive Javascript simulation of the HH model Runs in any HTML5 – capable browser. Allows for changing the parameters of the model and current injection.
- Interactive Java applet of the HH model Parameters of the model can be changed as well as excitation parameters and phase space plottings of all the variables is possible.
- Direct link to Hodgkin–Huxley model and a Description in BioModels Database
- Neural Impulses: The Action Potential In Action by Garrett Neske, The Wolfram Demonstrations Project
- Interactive Hodgkin–Huxley model by Shimon Marom, The Wolfram Demonstrations Project
- ModelDB A computational neuroscience source code database containing 4 versions (in different simulators) of the original Hodgkin–Huxley model and hundreds of models that apply the Hodgkin–Huxley model to other channels in many electrically excitable cell types.
- Several articles about the stochastic version of the model and its link with the original one.
编者推荐
集智课程
神经动力学模型读书会
人类大脑是一个由数以百亿计的神经元相互连接所构成的复杂系统。自神经科学这一学科建立以来,从解析神经元之间的相互作用机理、到刻画皮层柱之间的连接形式、再到探究脑区间不同认知功能的分离与整合模式,无数科学家试图从不同尺度研究大脑,以期揭示人脑这一最为复杂的神经系统的工作模式,进而理解语言、情绪、记忆和社会交往等高级认知活动的底层神经机制,并一定程度上启发通用人工智能机器人的设计。
近年来,脱胎于系统科学的动力学建模方法,逐渐被广泛地应用于神经科学研究中,其作为一种绝佳的数理工具,愈发地受到研究人员的重视,在类脑计算、脑认知原理解析和脑重大疾病致病机理探索等具体方面,发挥着不可替代的作用。
本着促进神经科学、系统科学以及计算机科学等不同领域的学术工作者的交流与合作,激发有志于加入脑科学与类脑研究这一领域的同学们的研究兴趣,来自国内外多所知名高校的专家学者(详见发起人介绍)共同发起了「神经动力学模型」读书会,聚焦于神经科学中的动力学建模这一前沿课题,讨论他们在研究一线中遇到的实际困惑,对相关文献进行深入梳理、激发跨学科的学术火花。
推荐书籍
《神经科学的数学基础》
该书原作为《Mathematical Foundations of Neuroscience》,由G.Bard Ermentrout, David H.Terman著,由吴莹,刘深泉译,为应用非线性动力学的方法来解决神经科学中的问题,包括利用现代数学建模方法理解各类试验中出现的神经放电模式。作者采用了多种非常广泛的方法来研究神经元以及神经回路的复杂模型,并结合数值模拟、解析法、动力学系统及扰动方法来分析多种类型的神经科学相关模型,形成一种新的现代理论。书中还分析了噪声、时间尺度效应以及空间相关性,解释了神经科学实验中出现的复杂的行为模式。
本书1.9节详细论述了本词条内容。
本中文词条由安贞桦翻译,安贞桦、薄荷编辑,如有问题,欢迎在讨论页面留言。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。