断点回归

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
薄荷（讨论 | 贡献）2022年4月23日 (六) 16:44的版本
跳到导航 跳到搜索


在统计学、计量经济学、政治学、流行病学和相关学科中，断点回归 regression discontinuity design (RDD)是一种准实验性的前后侧设计，其目的是通过设定一个临界值或阈值，其两侧即为干预效果的分配。通过比较临近阈值两侧的观测值，可以估计在随机化试验不可行的条件下的平均处理效果。然而，仅使用这种方法仍然不能做出完全的因果推断，因为它不会自动排除任何潜在的混杂变量。RDD最初由Donald Thistlethwaite和Donald T. Campbell应用于奖学金项目的评估，[1]近年来越来越受到欢迎。[2]最近的随机对照试验(RCTs)和RDD的研究比较已经经验性地证明了该设计的内部有效性。[3]

实例

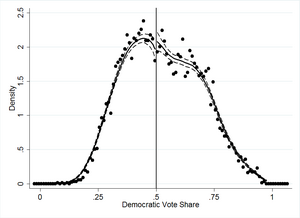
通过对基于成绩来判断是否获得奖学金的一项评估，可以很好地说明RDD背后的直觉。估计这种干预的因果效应的主要问题是分配至处理组的样本的表现具有同质性(如：均获得奖学金或均未获得奖学金)。因为表现优异的学生更有可能获得优异奖学金，同时这些学生在未来将继续表现良好，因此比较获奖学金学生和未获奖学金学生的成绩，会使估计结果偏高。即使奖学金根本没有提高学生的成绩，获奖学金学生的成绩也会比没有获奖学金的成绩要好，这是因为奖学金是颁发给原本就表现良好的学生。


尽管缺乏一个实验设计，但一个RDD研究可以利用干预的外部特征来引出因果效应。如果给予所有特定分数以上的学生（如80分）奖学金，就能够通过比较在80分临界值附近的学生，得出局部处理效果。这里的经济学直觉是，一个得分79分的学生很可能与一个得分81分的学生非常相似--假设预先设定的临界值是80分。但不同的是，得分是81分的学生将获得奖学金，而79分的学生不会获得奖学金。将获得奖学金（处理组）的干预效果与未获得奖学金（对照组）的反事实处理效果进行比较，可以得到局部处理效果。


方法

使用RDD进行估计的两种最常见的方法是参数方法和非参数方法（通常是多项式回归)。

非参数估计

在RDD中最常见的非参数方法是局部线性回归。它的形式是:

[math]\displaystyle{ Y = \alpha + \tau D + \beta_{1}(X-c) + \beta_{2}D(X-c) + \varepsilon , }[/math]

其中[math]\displaystyle{ c }[/math]是处理临界值，[math]\displaystyle{ D }[/math]是一个二值变量，如果[math]\displaystyle{ X \ge c }[/math]是一个二进制变量，如果[math]\displaystyle{ h }[/math]是所用数据的带宽，我们有[math]\displaystyle{ c - h \le X \le c + h }[/math]。不同的斜坡和拦截符合截止线两侧的数据。通常使用矩形核心(不加权)或三角形核心。研究倾向于三角形核[4]，而矩形核有更直接的解释。[5]


在RDD中使用非参数方法的主要好处是，它提供了基于更接近临界值的数据的估计，这是直观上的好处。这减少了在估计临界点的不连续性时由于数据距离临界点太远而带来的一些偏差。[5]更近一步地说，局部线性回归是首选，因为它具有更好的偏差性质[4]和收敛性。如果可行的话，这两种类型的估计都是有效的方法，[6]然而，可以证明回归估计的结果并不过分依赖于所采取的特定方法本身。


参数估计

参数估计的一个例子是

[math]\displaystyle{ Y = \alpha + \beta_1 x_i + \beta_2 c_i + \beta_3 c_i^2 + \beta_4 c_i^3 + \varepsilon , }[/math]

其中，

[math]\displaystyle{ x_i= \begin{cases} 1\text{ if }c_i \geq \bar{c}\\ 0\text{ if }c_i \lt \bar{c} \end{cases} }[/math]

[math]\displaystyle{ \bar{c} }[/math] 是处理方法。注意，多项式部分可根据需要缩短或扩展。


其他例子

  • 由年龄资格标准确定干预与否的政策（如：养老金政策，最低法定饮酒年龄）[7][8]
  • 一个政治家以微弱优势获胜的选举。[9][10]
  • 在教育研究领域中分数线将学生分类到干预项目中。[11]


所需假设

断点回归设计要求除了干预变量和结果变量之外，所有潜在的协变量在断点处均应是连续的，一个充分但非必要的条件是，[10]干预分配在临界值处“和随机分配一样好”。[9]如果这种说法成立，那就保证了接受干预的样本与那些没有接受干预的样本是可比的，因为干预与否在断点处实际上是随机的。


如果分配变量和代理变量(个人、公司等)是随机的，那么代理变量由于不能完全控制干预分配会使RDD在临界值处变得“和随机试验一样好”。例如，假设一项干预是通过一个考试，考试成绩必须在总分的50%以上。在这种情况下，只要成绩是随机的,即无论这种随机性来源于随机的评分标准还是随机的学生表现，这个例子都是一个有效的RDD。


同时学生不能操纵他们的分数，从而改变自己的干预状态。举两个例子，学生说服老师使其通过分数线，或学生被允许重新参加考试。前一种情况下，那些没有通过分数线但是说服了老师的学生不同于那些没有通过分数线也没有说服老师的学生。这产生了选择偏差，因为现在干预组和控制组的学生存在差别，即潜在的协变量在两组学生中是不连续的，不满足以上假设。后一种情况下，一些学生可能决定重新参加考试，一旦通过就停止重考，这也导致了选择偏差，因为只有一部分学生会决定重新参加考试，即那些第一次就未通过分数线的学生。[5]


测试假设的有效性

如果代理变量能够确定他们的干预状态，那么就不可能准确地检验这些假设的有效性。幸运的是，一些测试可以提供证据支持或忽视RDD设计的有效性。


密度测试

McCrary (2008)[12]对 Lee，Moretti 和 Butler (2004)[13]的数据进行了密度测试。

McCrary (2008)建议检查分配变量的观测值密度。[12]假设在干预的临界值处赋值变量的密度存在不连续性。在这种情况下，这可能表明一些代理变量能够改变他们的干预状态。


例如，如果一些学生说服老师通过了成绩，那么勉强通过考试的学生数量会比差点通过考试的学生多。同样地，如果允许学生重新参加考试直到他们通过，也会有类似的结果。在这两种情况下--可以通过检查考试成绩在临界值处的密度，“博弈系统”可能会对干预效果的估计产生偏差。


连续的可观察变量

由于RDD设计的有效性依赖于那些受到干预的样本和未受到干预的样本特征的相似性，所以检查这些样本是否具有相同的可观测变量值是有意义的。对于前面的例子，我们可以测试那些通过分数线的学生和那些未通过分数线的学生是否有相同的特征（人口统计资料、家庭收入等）。虽然一些变量可能会因为随机因素而有所差异，但大多数变量应该是相似的。[13]


伪造测试

事前变量

类似于可观测变量的连续性，事前变量在临界值处也将是连续的，因为这些变量是在干预之前就已经确定的，干预状态不会影响他们。考虑之前基于考试成绩来确定是否获得奖学金的例子，如果感兴趣的结果变量是未来的成绩，那奖学金不会影响事前就已经确定的考试成绩。如果事前变量在临界值处是不连续的，那RDD的有效性将成为问题。


其他非连续性

如果在分配变量的其他点存在不连续性，那么这可能使RDD设计受到质疑。[8]以Carpenter and Dobkin(2011)为例，他们研究了美国饮酒合法化的影响。随着21岁人群接触酒精的机会增加，这会导致各种变量结果的改变，如死亡率和发病率。如果死亡率和发病率在其他年龄段也不连续地增加，那么21岁时这种不连续性的解释就成为问题。


协变量的包含和排除

如果参数估计对排除或增加模型的协变量很敏感，那么这可能会对RDD的有效性提出挑战。一个显著的变化可能表明那些得到干预的样本和那些没有得到干预的样本在这些协变量上有所不同。加入协变量可以消除一些偏差。如果偏差过大，并且协变量可以解释绝大部分偏差，那么包含或者排除这些协变量将显著改变参数估计值。[5]


最近的工作已经展示了如何添加协变量，在什么条件下是最有效的，以及提高精度的潜力。[14]


优势

  • 当正确实施和分析研究时，RDD 产生了对局部处理效果的无偏估计。[15]在测量处理效果方面，RDD 几乎可以和随机实验一样好。
  • 作为一项准实验，RDD不需要事先随机化，并规避随机分配的道德问题。
  • 符合假设的RDD研究可以产生类似于随机研究估计的处理效果估计。[16]


缺点

  • 只有正确地模拟了处理变量和结果变量之间的函数形式，估计的效果才是无偏的。常见的误区是不连续的非线性关系被认误认为是断点。
  • 受其他处理事件的干扰。假设在相同赋值变量的相同截点处发生另一个冲击。在这种情况下，测量的结果变量的不连续性可能部分归因于这一冲击。例如，假设一位研究人员希望在法定最低饮酒年龄采用回归间断设计来研究合法饮酒对心理健康的影响。衡量的影响可能会与另一法规--合法参与赌博相混淆，后者恰好在同一年龄段。


扩展

扩展

因果关系的确定取决于一个关键的假设，即确实存在一个明显的临界点，在这个临界点周围存在着从0到1的分配概率的不连续性。然而，在现实中，截断通常不是严格执行的(例如:。对于未能通过门槛的学生行使酌情权) ，因此估计会有偏差。


与精确断点回归设计相比，模糊断点回归 fuzzy regression discontinuity design(FRDD)不要求分配概率是0和1。尽管如此，只要分配的概率不同，它仍然是适用的。这背后的直觉与工具变量/干预策略和干预意图有关。


回归扭结设计

当分配变量是连续的（如：学生补助）并且由其他观测变量决定（如：家庭收入），那么我们可以使用处理函数的斜率在精确断点的变化来辨别出处理效应。这项技术被称为kink断点回归，由Nielsen, Sørensen, and Taber (2010)设计，虽然他们引用了早前的研究。[17]他们写道：“这种方法类似于断点回归的思想。我们没有看到津贴-收入函数水平的不连续性，而是看到了函数斜率的不连续性。”Card et al. (2012)[18]在此基础上提供了严格的理论基础，并且Bockerman et al. (2018)将此应用于实证分析。[19]


请注意，kink回归也可以理解为一种分段回归，这是一种不同类型的分析。


最后的考虑

RD设计采用准实验研究设计的形式，结构清晰，没有随机化的实验特征。但RD设计也存在一些问题，例如，设计通常会涉及一些严重的问题，即无法提供随机试验的场景；此外，试验的设计取决于建模过程的准确性和自变量与因变量之间的关系。


另见


参考文献

  1. ↑ Thistlethwaite, D.; Campbell, D. (1960). "Regression-Discontinuity Analysis: An alternative to the ex post facto experiment". Journal of Educational Psychology. 51 (6): 309–317. doi:10.1037/h0044319.
  2. ↑ Imbens, G.; Lemieux, T. (2008). "Regression Discontinuity Designs: A Guide to Practice" (PDF). Journal of Econometrics. 142 (2): 615–635. doi:10.1016/j.jeconom.2007.05.001.
  3. ↑ Chaplin, Duncan D.; Cook, Thomas D.; Zurovac, Jelena; Coopersmith, Jared S.; Finucane, Mariel M.; Vollmer, Lauren N.; Morris, Rebecca E. (2018). "The Internal and External Validity of the Regression Discontinuity Design: A Meta-Analysis of 15 Within-Study Comparisons". Journal of Policy Analysis and Management (in English). 37 (2): 403–429. doi:10.1002/pam.22051. ISSN 1520-6688.
  4. ↑ 4.0 4.1 Fan; Gijbels (1996). Local Polynomial Modelling and Its Applications. London: Chapman and Hall. ISBN 978-0-412-98321-4. 
  5. ↑ 5.0 5.1 5.2 5.3 Lee; Lemieux (2010). "Regression Discontinuity Designs in Economics". Journal of Economic Literature. 48 (2): 281–355. doi:10.1257/jel.48.2.281.
  6. ↑ Porter (2003). "Estimation in the Regression Discontinuity Model" (PDF). Unpublished Manuscript.
  7. ↑ Duflo (2003). "Grandmothers and Granddaughters: Old-age Pensions and Intrahousehold Allocation in South Africa". World Bank Economic Review. 17 (1): 1–25. doi:10.1093/wber/lhg013. hdl:10986/17173.
  8. ↑ 8.0 8.1 Carpenter; Dobkin (2011). "The Minimum Legal Drinking Age and Public Health". Journal of Economic Perspectives. 25 (2): 133–156. doi:10.1257/jep.25.2.133. JSTOR 23049457. PMC 3182479. PMID 21595328.
  9. ↑ 9.0 9.1 Lee (2008). "Randomized Experiments from Non-random Selection in U.S. House Elections". Journal of Econometrics. 142 (2): 675–697. CiteSeerX 10.1.1.409.5179. doi:10.1016/j.jeconom.2007.05.004.
  10. ↑ 10.0 10.1 de la Cuesta, B; Imai, K (2016). "Misunderstandings About the Regression Discontinuity Design in the Study of Close Elections". Annual Review of Political Science. 19 (1): 375–396. doi:10.1146/annurev-polisci-032015-010115.
  11. ↑ Moss, B. G.; Yeaton, W. H.; Lloyd, J.E. (2014). "Evaluating the Effectiveness of Developmental Mathematics by Embedding a Randomized Experiment Within a Regression Discontinuity Design". Educational Evaluation and Policy Analysis. 36 (2): 170–185. doi:10.3102/0162373713504988.
  12. ↑ 12.0 12.1 McCrary (2008). "Manipulation of the Running Variable in the Regression Discontinuity Design: A Density Test". Journal of Econometrics. 142 (2): 698–714. CiteSeerX 10.1.1.395.6501. doi:10.1016/j.jeconom.2007.05.005.
  13. ↑ 13.0 13.1 Lee; Moretti; Butler (2004). "Do Voters Affect or Elect Policies? Evidence from the U.S. House". Quarterly Journal of Economics. 119 (3): 807–859. doi:10.1162/0033553041502153.
  14. ↑ Calonico; Cattaneo; Farrell; Titiunik (2018). "Regression Discontinuity Designs Using Covariates". arXiv:1809.03904 [econ.EM].
  15. ↑ Rubin (1977). "Assignment to Treatment on the Basis of a Covariate". Journal of Educational and Behavioral Statistics. 2 (1): 1–26. doi:10.3102/10769986002001001.
  16. ↑ Moss, B. G.; Yeaton, W. H.; Lloyd, J. E. (2014). "Evaluating the Effectiveness of Developmental Mathematics by Embedding a Randomized Experiment Within a Regression Discontinuity Design". Educational Evaluation and Policy Analysis. 36 (2): 170–185. doi:10.3102/0162373713504988.
  17. ↑ Nielsen, H. S.; Sørensen, T.; Taber, C. R. (2010). "Estimating the Effect of Student Aid on College Enrollment: Evidence from a Government Grant Policy Reform". American Economic Journal: Economic Policy. 2 (2): 185–215. doi:10.1257/pol.2.2.185. hdl:10419/35588. JSTOR 25760068.
  18. ↑ Card, David; Lee, David S.; Pei, Zhuan; Weber, Andrea (2012). "Nonlinear Policy Rules and the Identification and Estimation of Causal Effects in a Generalized Regression Kink Design". NBER Working Paper No. W18564. doi:10.3386/w18564. SSRN 2179402.
  19. ↑ Bockerman, Petri; Kanninen, Ohto; Suoniemi, Ilpo (2018). "A Kink that Makes You Sick: The Effect of Sick Pay on Absence". Journal of Applied Econometrics. 33 (4): 568–579. doi:10.1002/jae.2620.


进一步阅读


外部链接


编者推荐

集智课程

因果科学读书会第三季：因果+X

“因果”并不是一个新概念，而是一个已经在多个学科中使用了数十年的分析技术。通过前两季的分享，我们主要梳理了因果科学在计算机领域的前沿进展。如要融会贯通，我们需要回顾数十年来在社会学、经济学、医学、生物学等多个领域中，都是使用了什么样的因果模型、以什么样的范式、解决了什么样的问题。我们还要尝试进行对比和创新，看能否以现在的眼光，用其他的模型，为这些研究提供新的解决思路。


“因果+X”就是要让因果真正地应用于我们的科学研究中，不管你是来自计算机、数理统计领域，还是社会学、经济学、管理学领域，还是医学、生物学领域，我们希望共同探究出因果研究的范式，真正解决因果的多学科应用问题，乃至解决工业界的问题。


本中文词条由Wits审校，薄荷编辑，如有问题，欢迎在讨论页面留言。


本词条内容源自wikipedia及公开资料，遵守 CC3.0协议。

取自“https://wiki.swarma.org/index.php?title=断点回归&oldid=30624”