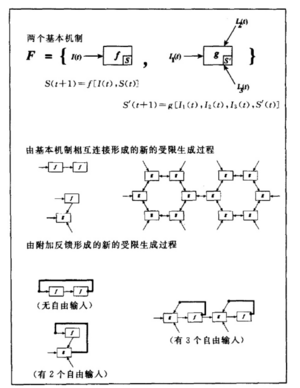
受限生成过程
此词条由自生成结构读书会词条梳理志愿者(The)构建,未经专家审核,带来阅读不便,请见谅。
受限生成过程 constrained generating procedures (cgp's) 是一个范围很广的模型的精确描述,是遵循科学家常用的有直观逐步走向精确的研究方法的结果。 由于生成模型是动态的,所以称之为“过程”;支撑这个模型的机制“生成”了动态的行为;而是事先规定好的机制间的相互作用“约束”或“限制”了这种可能性。事实上,任何受限生成过程都能表现涌现特性。
概括地说,对受限生成过程的理解包括以下四个步骤。
- 机制 需要将规则的概念转换成机制的概念。正如规则之于游戏,规则之于物质系统一样,机制被用来定义系统中的元素。机制根据行为(或信息)作出反应,对输入进行处理并产生最终的输出行为(或信息)。
- 将定义把多种机制连接起来形成网络的方法,这些网络就是受限生成过程。由于很多模型都设计不止一种机制(如物理学中的不同基本粒子),为了运用这种方法进行说明,必须明确机制的行为是如何影响其他机制的。
- 当这些机制连接起来,就会遇到类似于对策树的情况 - 由一些带约束条件的相互作用着的机制产生的所有可能性的集合。需要把这样的概念扩展到一般的系统。1)我们需要定义总的受限生成过程的状态,这个状态将由组成这个受限生成过程的状态决定。2)还需要将所有涉及将来可能性与受限生成过程有关的一切事物,提炼成被称为全局状态的一个单一实体。3)描述从一种状态转换到另一种状态的合法方式。
- 还需要提供受限生成过程中一个特别的过程,来定义子集合的层次,即使用基本机制建立起来更复杂的机制的过程。
机制 机制是通过转换函数来定义的。如在游戏的例子,会在定义策略函数之前,先定义游戏的状态。类似地,对于一个机制来说,定义转换函数之前,要定义机制的状态。
{S_{1}, S_2, S_3, ...} 来表示状态的集合S,下标表示可能存在的状态。将当前机制的输入值和当前的状态作为转换函数f的初始参数,就可以生成机制的下一个状态。为了将可能的输入参数和可能的状态在机制中表示出来,会给每个输入分配一个下标,即输入 j就会得到一组相关的符号 I_i = { i_{j1}, i_{j2}, i_{j3}, ...}。其中,i_{jh}中的下标j表示输入j的一个可能取值,h指明了输入j的可能状态。例i_{j2}就是输入j的第2种可能的状态。
下面定义描述机制中输入值的所有可能的组合集I为I_1,I_2,...,I_k的乘积,即 I = I_1 \times I_2 \times ... \times I_k。例如,有集合I_1 = {a, b , c}和 I_2= {x, y},则 I = I_1 \times I_2 = {(a,x), (a,y), (b,x), (b,y), (c,x), (c,y)}。通过上述办法,转换函数f可以定义成如下的函数
f : I \times S -> S,
或者,按照定义展开 I,即
f : (I_1 \times I_2 \times ... \times I_k) \times S -> S。
还需要符号来表示时刻t的机制状态和输入状态。令 S(t)为t时刻机制的状态,I_j (t)为t时刻输入j的状态(输入值),那么机制的运动状态-机制在一段时间内的行为由f按如下公式确定:
S(t+1) = f(I_1 (t), I_2 (t), ..., I_k (t), S(t))。
f 根据机制在t时刻的状态S(t)的赋值和输入{I_1 (t), I_2 (t), ..., I_k (t)}来决定机制在下一个瞬间时刻 (t+1)的状态S(t+1)。在输入组合序列 I(t), I(t+1), ...,的影响下,反复使用函数f可以生成连续的状态,即机制的状态曲线。这种反复迭代也是生成过程的特性。
相互作用和连接
在受限生成过程的定义中,最关心的是建立一个共同的基本的框架,以便能够在其中研究涌现的复杂性和展现涌现现象的各种例子,而这些现象则是由规则支配的实体相互作用产生得到。机制作为这些规则的表示形式,多个相似的机制相互作用时,涌现和生成的复杂性就会产生紧密的联系。
在受限生成过程的定义是从对集合的选择开始的,这里的集合是由称为初始因子的机制F构成的。当受限生成过程用来对游戏建立模型时,如神经网络、元胞自动机或其他表现涌现的系统,初始因子就是被用来构成模型的基本元素。
当一个机制的状态序列决定了另一个机制中的输入变量序列的值时,我们就说这两个机制相互连接。一旦选择了F,我们就将F中机制的片段相连构成一个相互作用的机制的网络。简言之,当选择初始因子F的一个集合,并将它们相互连接时,就可以获得一个特定的受限生成过程。
令F是m个基本机制的小集合,这些基本机制由转换函数 f_1,f_2,...,f_m定义。F中的机制可能有不同的状态集,不同的输入个数以及对每个输入来说不同的字母表示。即使用如下方式表示 I_h = I_{h1} \times I_{h2} \times ... \times I_{h k(h)}。这个式子表示机制h可能的输入连接,其中k(h)表示机制h的输入个数。通过扩展,机制h的转换函数 f_h将变成如下形式
f_h : I_h \times S_h -> S_h。
对受限生成过程加以定义后,如何使F中的机制相互作用仍然是一个待解决的问题。为了使两个机制能相互作用,其中一个机制的状态应当在一定程度上决定另外一个机制的输入值。因为这些机制有不同的状态集合和不同的输入字符,所以需要一个界面将机制的状态转换成另一个机制的合法输入。通过对F中机制的不同状态集取并集,可以定义界面函数,即 S= S_1 U ••• U S_m。通过形式化的表达,就能把S作为所有界面函数的初始值。
对于这些不同的输入符号和状态集,我们必须将界面函数g_{ij}和每个机制i中的每个输入量j联系起来。也就是说对于一个和机制i连接的机制,先讲输入j作为该机制的初始值,然后通过连接该机制的状态,函数g_{ij}就可以为机制i生成输入j的合法值。于是,g_{ij}被赋予如下的表达形式
g_{ij} : S -> I_{ij}。
我们说在任意时刻t,机制h与机制i的输入j相连接,
I_{ij}(t) = g_{ij}( S_h (t))
是指根据机制h在时刻t的状态S_h (t),通过界面函数g,就可以确定在时刻t的输入j,而没有连接的输入则被认为是自由的。对于自由输入,每一时刻的值将由外部环境(受限生成过程的外部)提供。实际上,自由输入也被计算在整个受限生成过程中输入的总个数里。
为了给受限生成过程提供一个完全的构造模型的空间,我们必须用不同的方法连接F中的机制片段。最简单的方法是确定一个更复杂的受限生成过程是如何从简单的受限生成过程创建的。下面将从最简单的受限生成过程,即一个单一的机制开始,然后再有步骤地达成我们的目标。
- 受限生成过程$C$可以由一个单一的机制 $f \in F$ 构成。
- 假设$C$为已经建立的受限生成过程,且$C$中的机制$i$有一个自由输入$j$。将输入$j$与$C$中的某个其他机制$h$连接(在$C$中建立从$h$到$i$的新连接),就能得到新的受限生成过程$C^{'}$。
- 假设$C_1$和$C_2$为已经建立的受限生成过程,且$C_1$中的机制$i$有一个自己有输入$j$。将输入$j$与$C_2$中的某个其他机制$h$连接(这样,输入$j$就不再是自由的),就会得到一个新的受限生成过程$C^{''}$。
- 通过以上三步,就可以建立所有以$F$为基础的受限生成过程。
我们用n(C)来表示受限生成过程C中机制的总个数。那么集合{1,2,...,n(C)},就可以给受限生成过程C中每一个机制分配一个唯一表示。这些标识的简历,可以模拟受限生成过程的创建过程。
- 若一个受限生成过程$C$可以由一个单一的机制 $f \in F$ 构成,则f的标识就是 x =1。
- 若一个受限生成过程$C^{'}$是由$C$中的一个自由输入和其他机制连接构成,则表示不变。
- 若一个受限生成过程$C^{'}$是$C_1$和$C_2$通过将$C_1$的一个自由输入与$C_2$中的一个机制相连接形成的,则$C_1$的表示不变,$C_2$中的每一个表示x都增加n(C_1)以生成一个新的表示 x' = x + n(C_1),即 n(C') = n(C_1) + n(C_2)。
图1 由一系列基本机制生成的受限生成过程
如图1 展示了由一系列基本机制生成的受限生成过程
• 有限生成群,生成元/building blocks
• 输入 I
• 状态 S
• 机制 f ∶ I ×S → S
• 界面函数 g_{ij} ∶ S → I_{ij}, I_{ij}(t) = g_{ij}(S_h(t)).
将机制h与机制i的输入相连接
• 限制条件
总结
1. 涌现现象出现在生成系统之中
2. 在这样的生成系统中,整体大于部分之和
3. 生成系统中一种典型的涌现现象是组成部分不断改变的稳定模式
• 身体中的分子在不断更新
4. 涌现出来的稳定模式的功能是由其所处的环境决定的
5. 随着稳定模式的增加,模式间相互作用带来的约束和检验使得系统的功能也在增强
6. 稳定模式通常满足宏观规律
• Conway 模型中滑翔机行为的规律
7. 存在差别的稳定性是那些产生了涌现现象的规律的典型结果
8. 更高层的生成过程可以由稳定性的强化而产生
待建立 参考文献:《隐秩序》《涌现(第7章)》
“此词条暂由(The)构建、整理。”