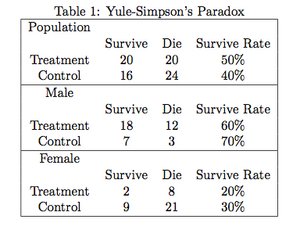
辛普森悖论
辛普森悖论 Simpson's paradox是一个统计学悖论。它是以Edward H. Simpson的名字命名的,他是一位英国统计学家,在1951年第一次描述了它[1]。统计学家卡尔·皮尔森在1899年描述了一个非常相似的效应[2]。Udny Yule 的描述可以追溯到1903年[3]。有时,这种现象被称为“尤尔-辛普森效应”。当观察小组的统计分数时,这些分数可能会发生变化,这取决于小组是逐一观察,还是将它们合并成一个更大的小组。这种情况经常发生在社会科学和医学统计中[4]。如果用频率数据来解释因果关系[5],人们可能会感到困惑。悖论的其他名称还包括反转悖论和合并悖论[6]。
该悖论指出:会存在着这样的数据。总体上的统计结果与其每一个子部分的统计结果相反。即存在如下的可能性:X和Y在边缘上正相关;但是给定另外一个变量Z后,在Z的每一个水平上,X和Y都负相关。
在Table 1 中,第一个表是整个人群的数据:接受处理和对照的人都是 40 人,处理有较高的存活率,因此处理对整个人群有 “正作用”。第二个表和第三个表是将整个人群用性别分层得到的,因为第一个表的四个格子数,分别是下面两个表对应格子数的和:
即20=18+2,20=12+8,16=7+9,24=3+21
奇怪的是,处理对男性有 “负作用”,对女性也有 “负作用”。一个处理对男性和女性都有 “负作用”,但是他对整个人群却有 “正作用”,由此,悖论产生。
有人可能会认为这种现象是由于随机性或者小样本的误差导致的。但是这个现象与样本量无关,与统计的误差也无关。比如,将上面的每个格子数乘以一个巨大的正数,上面的悖论依然存在。
如果从纯数学的角度,上面的悖论可以写成初等数学。
a/b<c/d;a'/b'<c'/d';a+a'/b+b'>c+c'/d+d'
这并无新奇之处。但是在统计上,这具有重要的意义——变量之间的相关关系可以完全的被第三个变量 “扭曲”。更严重的问题是,我们的收集的数据可能存在局限性,忽略潜在的“第三个变量” 可能改变已有的结论,而我们常常却一无所知。鉴于 Yule-Simpson 悖论的潜在可能,不少人认为,统计不可能用来研究因果关系,在观察性研究中很难得到有关因果的结论,除非加上很强的假定。比如,一个很经典的问题:吸烟是否导致肺癌?由于我们不可能对人群是否吸烟做随机化试验,我们得到的数据都是观察性的数据:即吸烟和肺癌之间的相关性 (正如 Table 1 的合并表)。此时,即使我们得到了吸烟与肺癌正相关,也不能断言 “吸烟导致肺癌”。这是因为可能存在一些未观测的因素,他既影响个体是否吸烟,同时影响个体是否得癌症。也许,某些基因可能使得人更容易吸烟,同时容易得肺癌;存在这样基因的人不吸烟,也同样得肺癌。此时,吸烟和肺癌之间相关,却没有因果作用。
此外,再考虑吸烟与收入之间的关系。根据有关统计数据,平均来说,吸烟人群比不吸烟人群收入更高;但是考虑吸烟人群的年龄因素时就可能会发现,在每个年龄组,吸烟人群的收入低于不吸烟的人群,如果再纳入年龄和学历这两个因素,可能就会发现相同年龄和学历的吸烟者比不吸烟收入高。可见,随着考虑的因素增多,统计结果会不断发生逆转。在类似这样的问题中,想要确定吸烟是否会影响收入以及影响有多大,仅从数据来看似乎无法获得准确的答案。
再比如,在我们知道放射性物质对人体的健康有很大的伤害的前提下,我们却发现铀矿的工人平均寿命却不比常人短;这是流行病学中有名的 “健康工人效应”(healthy worker effect)。这样一来,似乎是说铀矿工作对健康没有影响。但是,事实上,铀矿的工人通常都是身强力壮的人,不在铀矿工作寿命会更长。此时,在铀矿工作与否与寿命不相关,但是放射性物质对人的健康却确实是有因果作用的。
接下来通过一系列样例,详细了解辛普森悖论的现象。
样例
上面所提及的例子是人工构造的,而在现实中,也存在不少的实例正是辛普森悖论。比如,UC Berkeley 的著名统计学家 Peter Bickel 教授 1975 年在 Science 上发表文章,报告了 Berkeley 研究生院男女录取率的差异。他发现,总体上,男性的录取率高于女性,然而按照专业分层后,女性的录取率却高于男性。在流行病学的教科书 中,都会讲到 “混杂偏倚”(confounding bias),其实就是辛普森悖论,书中列举了很多流行病学的实际例子。下简单举四个样例便于理解。
样例1:肾结石治疗
这是一个真实的例子,来自一项医学研究[7],比较两种治疗肾结石的成功率[8]。
下表显示了治疗小肾结石和大肾结石的成功率和治疗次数,其中治疗A包括所有开放手术,治疗B是经皮肾镜取石术:
| 治疗方案A | 治疗方案B | |||
|---|---|---|---|---|
| 成功 | 失败 | 成功 | 失败 | |
| 小肾结石 | 第一组 | 第二组 | ||
| 患者数量 | 81 | 6 | 234 | 36 |
| 93% | 7% | 87% | 13% | |
| 大肾结石 | 第三组 | 第四组 | ||
| 患者数量 | 192 | 71 | 55 | 25 |
| 73% | 27% | 69% | 31% | |
| 既有小肾结石也有大肾结石 | 第一组和第三组 | 第二组和第四组 | ||
| 患者数量 | 273 | 77 | 289 | 61 |
| 78% | 22% | 83% | 17% | |
一个自相矛盾的结论是,A疗法对小结石更有效,对大结石也更有效,而B疗法在同时考虑两种大小时更有效。在这个例子中,还不知道肾结石的大小会影响结果。这在统计学中称为隐藏变量(或隐藏变量)。
哪种治疗方法更好是由两个比率(成功率/总成功率)之间的不平等决定的。造成辛普森悖论的两个比率之间不平等的逆转,是因为两种效应同时发生:
- 1、当忽略隐藏变量时,组的大小是非常不同的。医生倾向于对严重的病例(大结石)给予较好的治疗(A) ,对较轻的病例(小结石)给予较差的治疗(B)。因此,总数由第三组和第二组支配,而不是由规模小得多的第一组和第四组支配。
- 2、潜伏变量对比率有很大的影响,也就是说成功率更多地受到病情严重程度的影响,而不是治疗方法的选择。因此,治疗 A组(第三组)大结石患者的情况比治疗小结石患者差,即使后者采用劣等治疗 B 组(第二组)。
样例2:伯克利大学的招生歧视悖论
最著名的辛普森悖论的实例,就是1973年加利福尼亚大学伯克利分校性别歧视案的例子。
如果只看整体录取率,那么男生的录取率是44%,女生的是35%。
| 男生 | 女生 | |||
|---|---|---|---|---|
| 申请人数 | 录取人数 | 申请人数 | 录取人数 | |
| 合计 | 8442 | 44% | 4321 | 35% |
从表格可见,从整体录取率来看,男生的录取率是44%,女生的录取率是35%。从表面上看会得出结论,女生申请大学受到了歧视,但是若将数据按院系拆分,再来看每个系的录取率。
| 院系 | 男生 | 女生 | ||
|---|---|---|---|---|
| 申请人数 | 录取比例 | 申请人数 | 录取比例 | |
| A | 825 | 62% | 108 | 82% |
| B | 560 | 63% | 25 | 68% |
| C | 325 | 37% | 593 | 34% |
| D | 417 | 33% | 375 | 35% |
| E | 191 | 28% | 393 | 24% |
| F | 373 | 6% | 341 | 7% |
你可以看到,在6个院系的4个里,女生的录取率大于男生,女生只在2个院系里容易折戟。加利福尼亚大学伯克利分校的统计学教授 Peter Bickel 后来发现,如果按照这样的分类,女生实际上比男生的录取率还高一点点。
Bickel 认为,在这个案例中,辛普森悖论出现的原因是,女生更愿意申请那些竞争压力很大的院系(比如英语系),但是男生却更愿意申请那些相对容易进的院系(比如工程学系)
样例3:佛罗里达死刑悖论
1991年,科罗拉多大学的统计学家 Michael L. Radelet 和东北大学的社会学研究院主任 Glenn Pierce 重新查看了1976-1987年间美国佛罗里达州的谋杀案的审判数据,发现了重大的司法不公正事件。
从归总的数据来看,佛罗里达的法官在审判的时候并没有偏向白人,因为白人嫌疑人的死刑率甚至还比黑人高一些。
| 嫌疑人种族 | 死刑人数 | 非死刑人数 | 死刑百分比% |
|---|---|---|---|
| 白人 | 53 | 430 | 11 |
| 黑人 | 15 | 176 | 7.9 |
但是按照被害人的种族来分割数据的话,就会看到很不一样的结论,黑人比白人更容易被判死刑。
| 被害人种族 | 嫌疑人种族 | 死刑人数 | 非死刑人数 | 死刑百分比% |
|---|---|---|---|---|
| 白人 | 白人 | 53 | 414 | 11.3 |
| 白人 | 黑人 | 11 | 37 | 22.9 |
| 黑人 | 白人 | 0 | 16 | 0 |
| 黑人 | 黑人 | 4 | 139 | 2.8 |
由此可见不管被害人是什么种族,黑人比白人更有可能被判死刑,并且对比发现,如果受害人是白人,那么嫌疑人就更容易被判死刑。如果被害人是黑人,嫌疑人被判死刑的可能性很低。可见种族歧视是存在的
样例4 一种临床新药试验对比(考虑血压因素)
样例4中,我们知道药物会通过减低服药患者的血压来影响痊愈率,但不幸的是药物也会产生副作用。在这种情况下,我们需要根据数据判断是否给患者推荐这种药物。
下表记录治疗后700例患者的血压及其痊愈率。其中,350例患者服药,350例患者不服药。研究结果如下表
| 患者 | 患者未服用药物情况 | 患者服用药物情况 | ||
|---|---|---|---|---|
| 痊愈患者数 | 痊愈率/% | 痊愈患者数 | 痊愈率/% | |
| 患者血压低 | 81例(共87例) | 93 | 234例(共270例) | 87 |
| 患者血压高 | 192例(共263例) | 73 | 55例(共80例) | 69 |
| 合计 | 273例(共350例) | 78% | 289例(共350例) | 83 |
如表所示,第一行是血压患者低的情况下,患者未服用药物和患者服用药物的对比,第二行是血压患者高的情况下,治疗方案A和治疗方案B的对比,对全体受试者而言,服用药物比未服用药物痊愈率更高。但是按照血压进行划分之后,在治疗后血压偏高和治疗后血压偏低的亚群里,我们无法观测到这也的结果,而只能看出因药物副作用而降低痊愈率。
本试验的目的是评价药物痊愈率的总体影响。但是在这个例子中,由于降低血压是药物影响痊愈率的结果之一,所以基于血压的分类就变得没有意义了(如果在治疗前记录患者血压,并且假定仅有血压对治疗有影响,那么情形就不同了)。我们再次统计分析全体受试者的试验数据,发现药物治疗增加了痊愈的可能性,于是我们确定应该推荐药物治疗。
值得注意的是,样例4与前几个样例的区别在于,正确结论体现在总体数据,前几个样例的正确结论体现在分类后数据。
辛普森悖论的原因
由前面的例子可知,数据并没有为治疗决策给出足够的信息,例如,无法知道何时测定药物的作用,无法知道药物如何影响血压,也无法知道血压如何影响痊愈率。事实上,正如统计学教科书习惯性指出,相关性不是因果关系,利用统计方法并不能仅根据数据来确定因果关系,因此统计方法无法支持决策。
然而,统计学家一直以这种因果假设来解释数据。事实上,在辛普森悖论中,按性别进行分类后之所以会得到矛盾的结论,其本质源于我们确信治疗不能影响性别,如果可以的话,就不会得到悖论,因为我们可以很容易的假定数据背后的因果关系具有于按血压分类相同的结构,尽管“治疗不能影响性别”这一命题很平凡,但却不能通过数据来验证这一命题,也无法依据标准统计学写出其数学表达式。事实上,以上样例的联列表无法表达任何因果信息,而统计推理又通常是以联列表为基础的。
辛普森逆转和辛普森悖论
在探究辛普森悖论为何会令人困惑的问题时,我需要区分辛普森逆转和辛普森悖论这两个概念。
辛普森逆转,是一个纯粹的数学事实:在合并样本时,两个或多个不同的样本关于某一特定事件的相对频率出现反转,如表所示,在我们的例子中,我们可以看到两组相对频率:3/40>1/20(这是女性患者中服用D药者和未服用D药者的心脏病发作的相对频率),和 8/20>12/40(这是男性患者中用药者与不用药者的心脏病发作的相对频率)。然而,当我们把男女样本的数据合并在一起时,不等式的方向就 发生了逆转:(3+8)/(40+20)<(1+12)/(20+40)。
可见辛普森逆转是在进行统计聚合时,算术不等式的反转表现,并不让人意外。
辛普森悖论,就是建立在辛普森逆转这个数学事实之上的概念。现在让我们回到开头Table1这个最重要的例子,一个药物当“对男性有害”“对女性有害”“对人类有益”这三个陈述被理解为比例增减时,它们在数学上并不矛盾。然而,我们可能仍然认为这种情况在现实世界中不可能出现,因为一种药物不可能既导致心脏病 发作又防止心脏病发作。这种直觉是普遍的,像这个矛盾的例子就被称为辛普森悖论。
辛普森悖论提醒我们,在某些情况下,至少存在 一个统计趋势(无论是来自聚合数据、分层数据还是同时来自两者)无 法代表真正的因果效应。
| 患者 | 对照组(未服药) | 处理组(服药) | ||
|---|---|---|---|---|
| 心脏病发作 | 无心脏病发作 | 心脏病发作 | 无心脏病发作 | |
| 女性 | 1 | 19 | 3 | 37 |
| 男性 | 12 | 28 | 8 | 12 |
| 合计 | 13 | 47 | 11 | 49 |
如何避免辛普森悖论
混杂变量
在上述的事例中,出现辛普森悖论的很大一个原因是由于存在隐藏变量,因此这便提醒我们,在进行变量设计时,一是要尽量多查阅文献以了解自变量,因变量及其他重要变量之间的关系,二是需要相关的经验,能够敏锐的察觉到某个变量的重要性。
这个重要潜伏变量指的是与实验分析的因果都有关系的变量,这一变量的缺失可能会掩盖或颠倒研究变量的原有关系。
比如在录取率这个例子中,专业既与录取率有关,不同专业难度不同,录取率自然有差异,又与性别有关,女生和男生趋向报考的专业不同。因此专业就是一个重要潜伏变量。
参考文献
- ↑ Simpson, Edward H. (1951). "The Interpretation of Interaction in Contingency Tables". Journal of the Royal Statistical Society, Ser. B. 13: 238–241
- ↑ Pearson, Karl; Lee, A.; Bramley-Moore, L. (1899). "Genetic (reproductive) selection: Inheritance of fertility in man". Philosophical Translations of the Royal Statistical Society, Ser. A. 173: 534–539
- ↑ G. U. Yule (1903). "Notes on the Theory of Association of Attributes in Statistics". Biometrika. 2 (2): 121–134. doi:10.1093/biomet/2.2.121
- ↑ Clifford H. Wagner (February 1982). "Simpson's Paradox in Real Life". The American Statistician. 36 (1): 46–48. doi:10.2307/2684093. JSTOR 2684093.
- ↑ Judea Pearl. Causality: Models, Reasoning, and Inference, Cambridge University Press (2000, 2nd edition 2009). ISBN 0-521-77362-8.
- ↑ I. J. Good, Y. Mittal (June 1987). "The Amalgamation and Geometry of Two-by-Two Contingency Tables". The Annals of Statistics. 15 (2): 694–711. doi:10.1214/aos/1176350369. ISSN 0090-5364. JSTOR 2241334.
- ↑ C. R. Charig; D. R. Webb; S. R. Payne; O. E. Wickham (29 March 1986). "Comparison of treatment of renal calculi by open surgery, percutaneous nephrolithotomy, and extracorporeal shockwave lithotripsy". Br Med J (Clin Res Ed). 292 (6524): 879–882. doi:10.1136/bmj.292.6524.879. PMC 1339981. PMID 3083922.
- ↑ Steven A. Julious and Mark A. Mullee (1994-12-03). "Confounding and Simpson's paradox". BMJ. 309 (6967): 1480–1481. doi:10.1136/bmj.309.6967.1480. PMC 2541623. PMID 7804052
编者推荐
集智俱乐部文章
周日直播 | 从辛普森悖论谈起:因果效应中的混淆因子及可识别性
福利 | 因果推断会是下一个AI热潮吗?Judea Pearl《因果论》重磅上市!
集智课程
因果科学读书会第三季:因果+X
“因果”并不是一个新概念,而是一个已经在多个学科中使用了数十年的分析技术。通过前两季的分享,我们主要梳理了因果科学在计算机领域的前沿进展。如要融会贯通,我们需要回顾数十年来在社会学、经济学、医学、生物学等多个领域中,都是使用了什么样的因果模型、以什么样的范式、解决了什么样的问题。我们还要尝试进行对比和创新,看能否以现在的眼光,用其他的模型,为这些研究提供新的解决思路。
“因果+X”就是要让因果真正地应用于我们的科学研究中,不管你是来自计算机、数理统计领域,还是社会学、经济学、管理学领域,还是医学、生物学领域,我们希望共同探究出因果研究的范式,真正解决因果的多学科应用问题,乃至解决工业界的问题。
本中文词条由我是猫翻译,薄荷编辑,如有问题,欢迎在讨论页面留言。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。