稳定学习

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
跳到导航 跳到搜索

稳定学习是一种在保证机器学习预测性能的前提下，减小其在未知测试集上方差的方法。由于稳定学习假设在测试数据中存在多个环境，对模型的泛化能力有更高的要求。

机器学习面临的挑战[1]

机器学习模型已经在许多面向互联网的场景取得成功。在诸如预测点击量或对图像进行分类等应用场景中，模型做出错误决策的代价似乎并不高，因此从业者采用“性能驱动”的模式优化人工智能技术，即只关注该模型在完成目标任务时体现出的性能而不太关注技术发生错误时的风险。当任务环境发生变化，预测出现错误的时候，人们通过频繁地更新黑盒模型以保证预测的性能。然而，在诸如医疗保健、工业制造、金融和司法等与社会生活息息相关的领域，机器学习模型做出的错误预测的后果往往是难以接受的，这些场景也因此被称为风险敏感的场景。由于数据获取困难以及伦理问题，在风险敏感的场景中因为环境变化而重新训练机器学习模型的代价会比较昂贵，因此模型的短期预测性能之外的特性也十分重要。为了促进机器学习模型在更多风险敏感场景的应用，我们需要仔细分析机器学习模型面临的技术性风险，并采取办法克服这些风险。


缺乏稳定性指的是模型在未知环境下预测性能不稳定。由于目前大多数机器学习模型依赖于I.I.D.假设（Independent and identically distributed），即训练数据集和测试数据集的数据分布是相似的。在实践中，模型的应用环境常常是未知的，即可能出现的（测试数据集）分布是无法完全预见的，I.I.D.假设在这时会被破坏，模型的性能无法保证。缺乏可解释性是由于目前大多数现成的机器学习模型都是黑盒模型：算法过程和预测结果都不容易向人类解释。在风险敏感领域，由于错误决策会导致严重的后果，往往需要让人类留在决策循环中成为决策的最终的看门人。此时，通用的语言来让算法和人类理解和合作是必要的。最后，主流的机器学习模型可能会放大数据中存在的偏差，从而导致不公平的结果，因此是缺乏公平性的。


因为常见的机器学习算法是基于输入变量和输出变量的相关性做预测，当它遇到变量之间的虚假相关时，便无法避免上述三个风险因素。数据中的相关性能归类成三种模式：因果导致的相关，混淆导致的相关和选择性偏差导致的相关，如图1所示。

图1：相关性的三种模式，（a）因果相关；（b）混淆导致的相关；（c）数据选择性偏差导致的相关。


在这三种产生相关性的模式中，只有因果关系产生的相关性反映了变量之间的内在依赖关系；另外两种类型是对特征的联合分布和数据收集过程敏感的虚假相关。由于黑盒模型甚至没有尝试区分产生这些相关性的三种不同模式，它们的预测性能在很大程度上取决于测试分布与训练分布的偏离程度，从而导致在不同的测试分布下性能不稳定。同时，基于虚假相关性的预测模型也可能是不公平的，因为它还放大了选择性偏差。


崔鹏发表在Nature Machine Intelligence的观点论文中提出，为了从根本上解决稳定性、可解释性和公平性的风险，人们需要在机器学习框架中接受并强调因果关系。因果关系实际上刻画了数据生成机制，如果能够识别和估计数据的因果结构，预测建模自然可以作为副产品来解决。遵循着强调因果关系的技术路径，研究者必须解决因果推断的所有挑战。至此，机器学习和因果推断之间形成了共识。崔鹏老师团队和国内外其他团队在这个问题上进行了诸多探索，并形成了“稳定学习”的方向，朝着沟通机器学习和因果推断的目标前进。

稳定学习的提出[2]

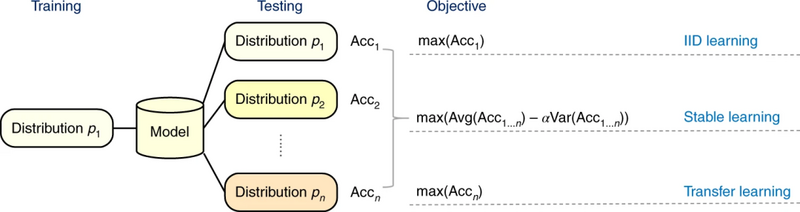
稳定学习的概念是在2018年的KDD会议上由清华大学副教授崔鹏团队提出的。它旨在解决这样一个问题，当我们用机器学习进行预测建模的时候，如果对测试数据集没有任何先验知识，如何保证模型在未知分布上做出稳定预测，即在保证预测性能的同时，尽量减小它在未知测试集的方差。图2展示了稳定学习和传统机器学习（独立同分布学习, I.I.D.）与迁移学习的关系，后两者的优化目标是在具有测试集分布先验知识的情况下，最大化模型的预测性能（准确率）。同时，稳定学习假设在测试数据中存在多个环境，因此对模型的泛化能力提出了更高的要求。

图2：稳定学习，传统机器学习（I.I.D.学习）和迁移学习的比较

在2018年发表在KDD会议的论文中，他们受到因果推断中利用协变量平衡估计因果效应的思想的启发，提出了一种新的深度全局平衡回归 Deep Global Balancing Regression（DGBR）算法，联合优化一个用于特征选择（降维）的深度自动编码器模型，和一个用于未知环境下稳定预测的全局平衡模型。这个全局平衡模型评估了任意一个特征在被隔离（isolated）的情况下，该个特征对响应的因果效应，并以此构建了一组使得变量被平衡（variable balancing）的样本权重，让加权后的样本的所有特征都尽可能相互独立。这个算法在高维度的数据中也适用。


稳定学习的主要方法

DGBR算法首次解决了二元预测变量（特征）和二元离散响应变量设定下的稳定预测问题。此后，一系列稳定学习方法来被提出来，用于解决更多不同设定下的稳定预测问题。而后续设计的稳定学习方法不仅仅再局限于因果推断的角度，还包括了统计学习、优化过程等不同视角，它们将在本节被逐一介绍。


基于样本加权的变量去相关[3][4][5]

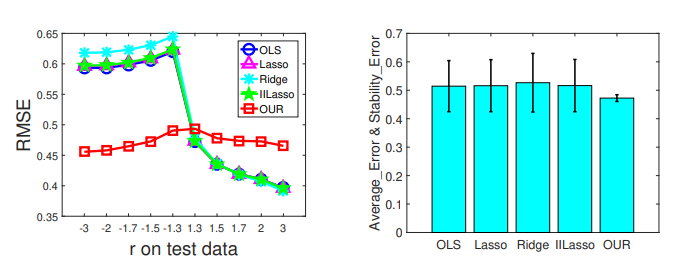
针对具有模型错估（model misspecification，即模型与数据生成机制不一致）稳定预测问题进行了进一步探索。Zheyan Shen等人研究了在线性模型中，变量间的共线性是如何影响预测稳定性的，并提出了一种一般的数据预处理方法，通过训练集样本重加权来去除预测变量（特征）间的相关性，以减小共线性效应。况琨等人的工作则进一步改进了DGBR算法，提出了去相关加权回归算法（Decorrelated Weighting Regression, DWR），结合了变量去相关正则化与加权回归模型，解决了在连续的预测变量（特征）的设定下，模型的稳定预测问题。

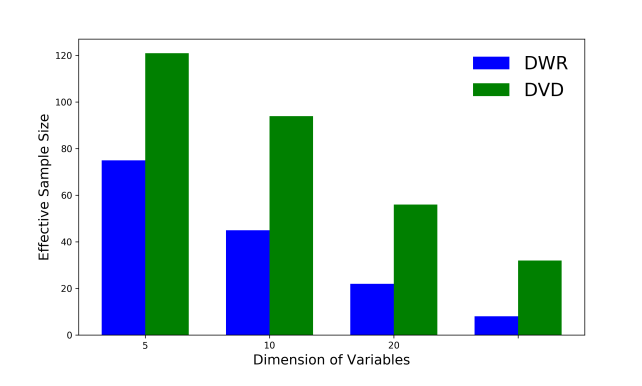
图3：DWR模型和基线模型在不同测试环境下性能的比较；左图：横轴代表不同的环境，纵轴代表预测误差，不同颜色代表不同的模型；右图：横轴代表不同的模型，纵轴代表在不同环境下的平均错误，性能的方差在条柱顶端用黑实线标出。

去除所有变量之间的相关性固然是找到因果相关，平衡协变量并实现稳定预测的好主意，它的代价是大大降低了有效样本量（efficient sample size），而这在机器学习训练中是灾难性的。Zheyan Shen等人通过使用来自不同环境的未标注数据，提出了一种基于变量聚类的变量分解的算法，称为区分性变量去相关（Differentiated Variable Decorrelation, DVD）。这个方法是注意到保留因果性变量之间的相关性未必会导致模型在未知环境中的性能不稳定。以特征间相关性的在训练集数据和未标注之间的数据稳定性作为聚类的指标，可以将预测变量（特征）进行聚类并为不同的聚类簇，其中一些聚类簇代表了对相应变量具有因果效应的特征集合。在平衡混淆变量时只需要隔离这些聚类簇即可。由于聚类簇的数量远低于特征的维度，因此DVD与样本加权方法DWR相比，保持了更高的有效样本量。

图4：与不加区分地去除所有变量的相关性的方法（DWR）相比，区分性变量去相关方法（DVD）在相同设定下具有更大的有效样本量。

对抗稳定学习[6]

由于人们总是想最大化地利用训练数据中发现的所有相关性，具有经验风险最小化的机器学习算法在分布变化下很容易受到攻击。崔鹏老师团队提出了稳定对抗学习 (Stable Adversarial Learning, SAL) 算法，以一种更有原则和统一的方式来解决这个问题，该算法利用异构数据源构建更实用的不确定性集并进行差异化鲁棒性优化，其中协变量根据其与目标相关性的稳定性进行区分。


具体来说，该方法就是采用了Wasserstein分布式鲁棒学习 Wasserstein distributionally robust learning（WDRL）的框架。根据协变量在多个环境中的稳定性，进一步将不确定性集表征为各向异性，这会给不稳定协变量带来比稳定协变量更强的对抗性扰动。并且设计了一种协同算法来联合优化协变量的微分过程以及模型参数的对抗训练过程。


在实验中，将SAL算法与经验风险最小化 Empirical Risk Minimization（ERM）框架、Wasserstein分布式鲁棒学习框架、不变风险最小化 Invariant Risk Minimization（IRM）框架进行比较：


图5：实验结果。(a)各环境下的测试性能。(b) 关于半径的测试性能。(c) S和V相对于半径的学习系数值。

实验结果表明，SAL算法各向异性地考虑每个协变量以实现更真实的鲁棒性。并且构建了一个更好的不确定性集，在不同分布的数据上取得了一致更好的表现，验证了算法的有效性。


异质性风险最小化[7][8]

同样地，如果想完全利用训练数据中发现的所有相关性，具有经验风险最小化的机器学习算法通常还会具有较差的泛化性能，这些相关性在分布变化下不稳定。崔鹏提出了异质性风险最小化 Heterogeneous Risk Minimization（HRM）框架，以实现对数据之间潜在异质性和不变关系的联合学习，从而在分布变化的情况下实现稳定的预测。

图6：HRM框架


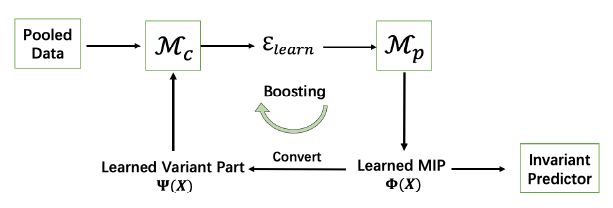
总体框架如图6所示，该框架包含两个模块，用于异质性识别的前端和用于不变预测的后端Mp。给定异质性数据，它从异质性识别模块Mc开始，利用学习的变体Ψ(X)表示生成异质性环境εlearn。然后分布外泛化预测模块Mp使用学习到的环境来学习MIPΦ(X)以及不变预测模型f(Φ(X))。之后，我们推导出变体Ψ(X)以进一步提升模块Mc。至于“转换”步骤，基于我们的设定，我们在这项工作中采用了特征选择，通过它可以在学习更多不变的特征时获得更多的变异特征。


HRM是一种优化框架，可实现数据和不变预测器之间潜在异质性的联合学习。尽管分布发生变化，在该框架下仍具有更好的泛化能力。


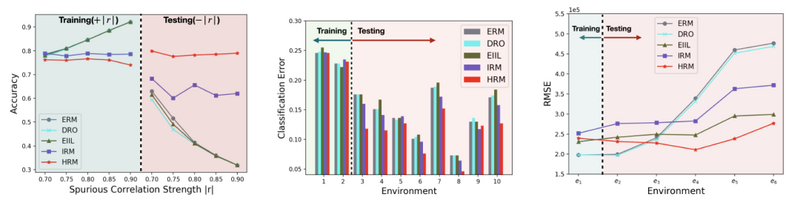
为了验证该框架的有效性，崔鹏老师团队将HRM框架与经验风险最小化框架、分布鲁棒优化 Distributionally Robust Optimization（DRO）框架、不变学习的环境推理 Environment Inference for Invariant Learning（EIIL）框架、具有环境εtr标签的不变风险最小化 (IRM) 框架进行比较。


实验表明，与基线方法相比，HRM在平均性能和稳定性方面取得了近乎完美的表现，尤其是跨环境损失的方差接近于0。此外，HRM不需要环境标签，这验证了我们的聚类算法可以挖掘数据内部潜在的异质性。


继续进行了三个真实场景的预测，包括汽车保险预测、人们收入预测和房价预测。

图7：真实场景的预测结果。(a) 汽车保险预测的训练和测试准确性。左子图显示了5种设置的训练结果，右子图显示了它们对应的测试结果。(b) 收入预测的误分类率。(c) 房价预测的预测误差。


从实验结果可以看出，在所有任务和几乎所有测试环境中，HRM始终保持最佳性能。HRM可以有效地揭示和充分利用训练数据的内在异质性进行不变学习。HRM放宽了对环境标签的要求，为不变学习开辟了新的方向。它能够涵盖广泛的应用，例如医疗保健、金融、营销等。


稳定学习的理论解释[9]

协变量偏移泛化是分布外泛化 (out-of-distribution, OOD) 中的典型案例，它要求在未知测试分布上具有良好的性能，并且该测试分布与训练分布差距体现在协变量迁移上。在涉及回归算法和深度神经网络的几种学习模型上，稳定的学习算法在处理协变量移位泛化方面已经显示出一定的有效性。崔鹏老师团队通过将稳定学习算法解释为特征选择的过程，向理论分析迈进了一步。


具体是这样的，首先定义一组变量，称为最小稳定变量集（minimal stable variable set），它是处理常见损失函数（包括均方损失和二元交叉熵损失）下的协变量迁移泛化的最小且最优的变量集合。然后证明了在理想条件下，稳定的学习算法可以识别出这个集合中的变量。这些理论阐明了为什么稳定学习适用于协变量迁移泛化。


典型稳定学习算法的框架如算法1所示。该算法通常包括两个步骤，分别是重要性采样和加权最小二乘。在理想条件下，稳定学习算法可以识别最小稳定变量集，这是可以在协变量偏移下提供良好预测的最小变量集。


最小稳定变量集与马尔可夫边界密切相关，稳定学习在一定程度上有助于识别马尔可夫边界。此外，如果以协变量移位泛化为目标，马尔可夫边界不是必需的，而最小稳定变量集是充分且最优的。


与马尔可夫边界相比，最小稳定变量集可以带来两个优势。

  1. 条件独立性检验是精确发现马尔可夫边界的关键。
  2. 在几个常见的机器学习任务中，包括回归和二元分类，并不是所有的变量都在马尔可夫边界。最小稳定变量集被证明是马尔可夫边界的子集，它排除了马尔可夫边界中无用的变量，用于协变量移位泛化。


稳定学习的应用

图上的稳定学习

具有选择性偏差的多个环境中学习稳定图[10]

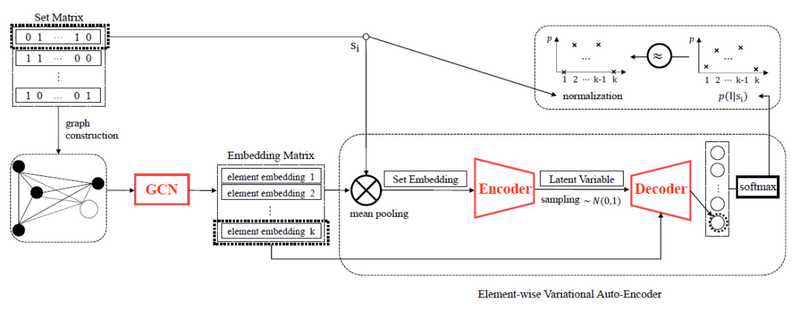
如今，图已成为一种通用且强大的表示，通过其结构中编码的底层模式来描述不同类型实体之间的丰富关系。然而，图生成的数据收集过程充满了已知或未知的样本选择性偏差，尤其是在非平稳和异构的环境中，实体之间会存在虚假关联。针对从具有选择性偏差的多个环境中学习稳定图的问题，崔鹏老师团队设计了一个无监督的稳定图学习 (Stable Graph Learning, SGL) 框架，用于从集合数据中学习稳定图，该框架由GCN (Graph Convolutional Networks) 模块和针对高维稀疏集合数据的E-VAE (element-wise VAE) 模块组成。


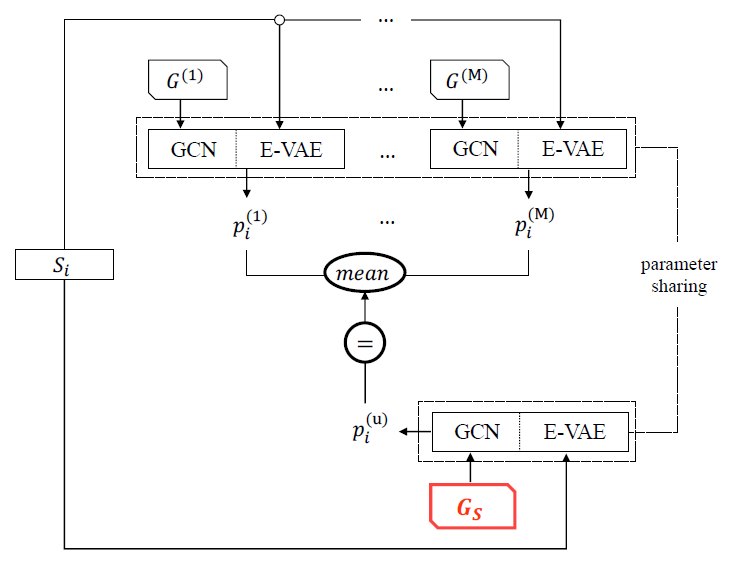
稳定图学习的任务是学习一个表示无偏连接结构的图Gs，因为环境中的图是从数据生成的，如果数据的收集过程来自具有选择性偏差的环境，则元素之间的虚假相关性会导致图在其他环境中表现不佳。SGL框架能很好地解决这个问题，SGL框架可以分解为两个步骤，包括基于图的集合生成和稳定图学习。基于图的集合生成的详细框架如图8所示。

图8：基于图的集合生成的详细框架。

稳定图学习过程图解如图9所示。

图9：稳定图学习的过程图解。

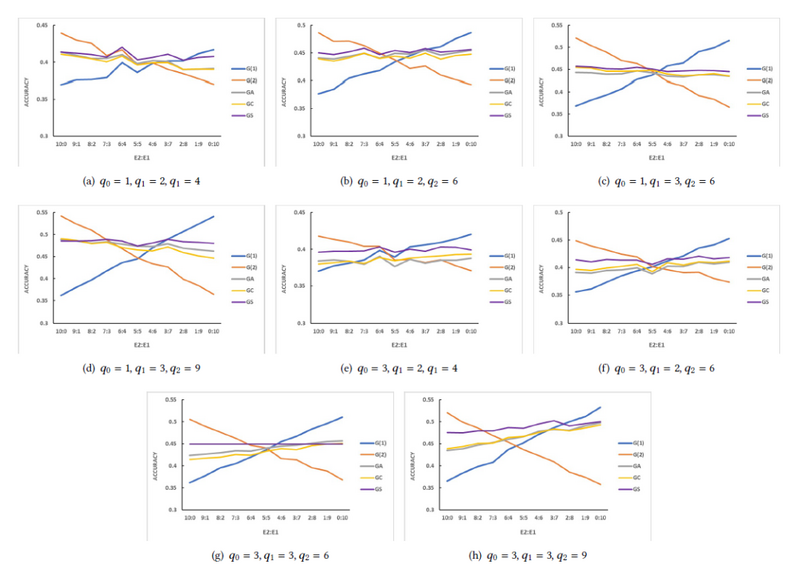
在模拟实验中，如图10所示，在几乎所有的实验中，SGL框架的性能要稳定得多，特别是当两个环境之间的差异更显着时，它比所有基线方法都达到更高的平均准确度。

图10：模拟实验结果。每个子图对应一个实验，紫色曲线表示SGL框架生成的图Gs的实验表现。

而相应地，在真实实验里，崔鹏老师团队研究了商品推荐的常见实际应用中的稳定图结构问题。

从表1可以看出，SGL框架生成的图Gs可以平衡两种环境下的相关性，更稳定地达到最高平均预测率。

表1：使用从商品网络中学习的项目嵌入进行带有曝光偏差的购买行为预测。

如表2所示。SGL框架可以很好地弥补单一环境下的信息损失，通过学习商品之间的本质关系，生成整体性能最佳的图Gs。

表2：使用从商品网络中学习到的项目嵌入来预测不同性别群体的购买行为。

图生成的数据选择性偏差可能导致有偏差的图结构在Non-I.I.D.场景中性能不佳。针对该问题提出的SGL框架可以提高学习图的泛化能力，并能很好地适应不同类型的图表和收集的数据。


具有不可知分布偏移的图的稳定预测[11]

图神经网络 Graph Neural Networks（GNNs）已被证明在具有随机分离的训练和测试数据的各种图任务上是有效的。然而，在实际应用中，训练图的分布可能与测试图的分布不同。此外，在训练GNNs时，测试数据的分布始终是不可知的。因此，大家面临着图学习训练和测试之间的不可知分布转变，这将导致传统GNNs在不同测试环境中的推理不稳定。


为了解决这个问题，浙江大学助理教授况琨提出了一种新的GNNs稳定预测框架，它允许在图上进行局部和全局稳定的学习和预测,可以减少异构环境中的训练损失，从而使GNNs能够很好地泛化。换句话说，是为GNNs设计了一种新的稳定预测框架，该框架能捕获每个节点的稳定属性，在此基础上学习节点表示并进行预测（局部稳定），并规范GNNs在异构环境中的训练（全局稳定）。该方法的本质如图11所示。

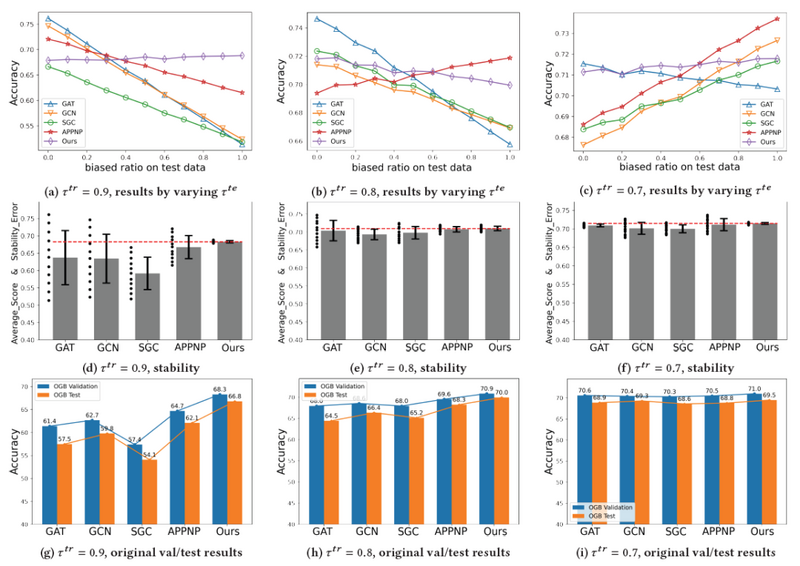
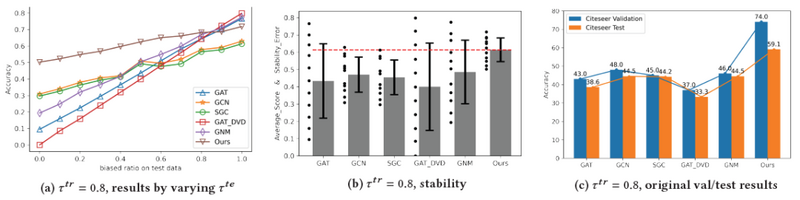
图11：整体架构。由两个基本组成部分组成，即在每个目标节点的表示学习中捕获跨环境稳定的属性的局部稳定学习，以及显式平衡不同训练的全局稳定学习环境。

在图基准实验中，况琨团队使用OGB数据集和传统基准Citeseer数据集，构建两层GCN和GAT。所有其他方法（包括我们的方法）也包含两个图形层以进行公平比较。OGBarxiv的所有方法的隐藏层神经节点个数为250，Citeseer的隐藏层神经节点个数为64，学习率为0.002。


测试结果如图12和图13所示。稳定预测框架有着更稳定的实验结果。当测试分布与训练分布的差异更大时，大多数GNNs会遭受分布变化并且产生较差的性能（例如，图12a的右侧）。尽管稳定预测框架在分布更接近训练的测试环境中牺牲了一些性能（例如，图12a的左侧），但获得了显着更高的 Average_Score 和更低的 Stability_Error。


图12：在OGB-Arxiv数据集上的测试结果。
图13：在Citeseer数据集上的测试结果

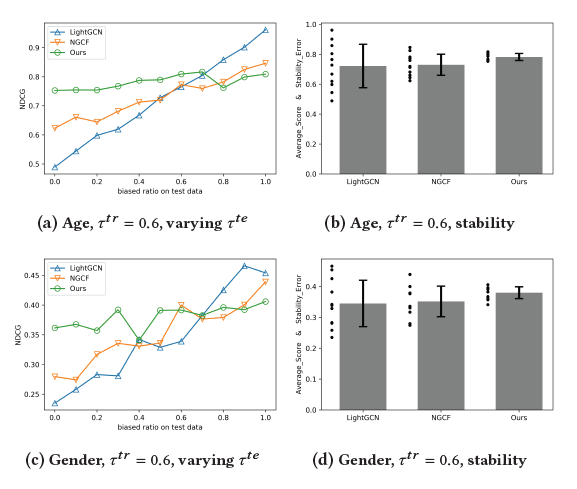
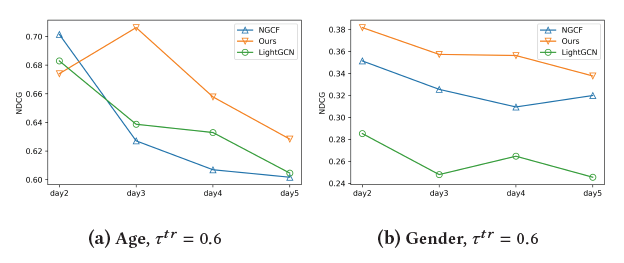
为了证明稳定预测框架在实际应用中的有效性，他们收集真实世界的嘈杂数据集，对推荐系统的用户-项目二分图进行了实验。如图14、15的实验结果表明，稳定预测框架比其他基线方法取得了明显更稳定的结果。

图14：具有由节点属性引起的分布偏移的真实世界推荐数据集的结果。
图15：具有真实世界环境的推荐数据集的结果（每天作为一个单独的环境）。

深度神经网络中的稳定学习[12]

基于深度神经网络的方法在测试数据和训练数据共享相似分布时取得了惊人的性能，但有时可能会失败。因此，消除训练和测试数据之间分布变化的影响对于构建性能有希望的深度模型至关重要。崔鹏建议通过学习训练样本的权重来消除特征之间的依赖关系来解决这个问题，这有助于深度模型摆脱虚假关联，进而更多地关注判别特征和标签之间的真正联系。


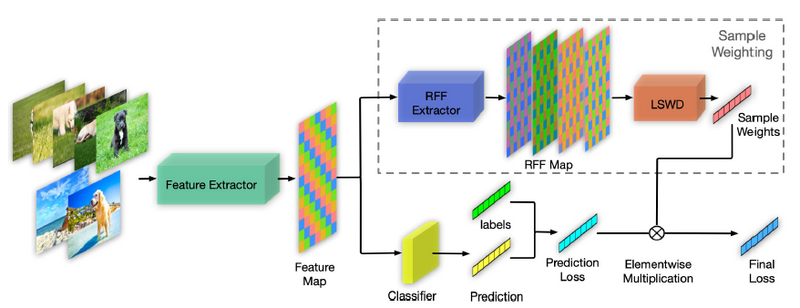
崔鹏提出了一种称为StableNet的方法。该方法通过全局加权样本来解决分布偏移问题，以直接对每个输入样本的所有特征进行去相关，从而消除相关和不相关特征之间的统计相关性。这是一种基于随机傅立叶特征 (Random Fourier Features, RFF) 的新型非线性特征去相关方法，具有线性计算复杂度。同时，它也是有效的优化机制，通过迭代保存和重新加载模型的特征和权重来全局感知和消除相关性，还能在训练数据量大时减少存储的使用和计算成本。此外，如图16所示，StableNet可以有效地剔除不相关的特征（例如，水）并利用真正相关的特征进行预测，从而在野外非平稳环境中获得更稳定的性能。

图16：当识别狗的训练图像包含很多水时，StableNet模型主要关注于狗。
图17：StableNet的整体架构。


为了涵盖更普遍和更具挑战性的分布变化案例，崔鹏老师团队在实验中采用如下四种设置：非平衡、灵活、对抗、经典。在不同的实验设置下，StableNet都能不同程度得优于其他方法。


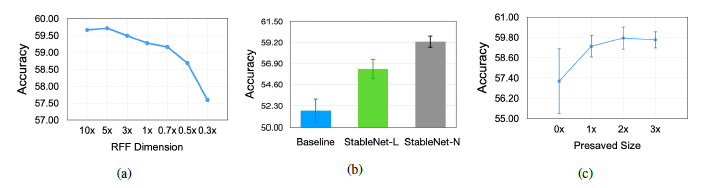
在消融研究中，通过随机选择用于计算具有不同比率的依赖关系的特征来进一步降低特征维度。图18显示了具有不同维度随机傅里叶特征的实验结果。

图18：消融研究的结果。


图像分类模型的一种直观解释是识别对最终决策有很大影响的像素。所以，在显着性图像上，为了演示模型在进行预测时是关注对象还是上下文（域），对类别得分函数相对于输入像素的梯度进行了可视化。可视化结果如图19所示。

图19：StableNet的显着性图像。像素越亮，它对预测的贡献就越大。


各种实验结果表明，StableNet方法可以通过样本加权消除相关和不相关特征之间的统计相关性，进而有效剔除不相关的特征并利用真正相关的特征进行预测。


稳定学习与公平性[13]

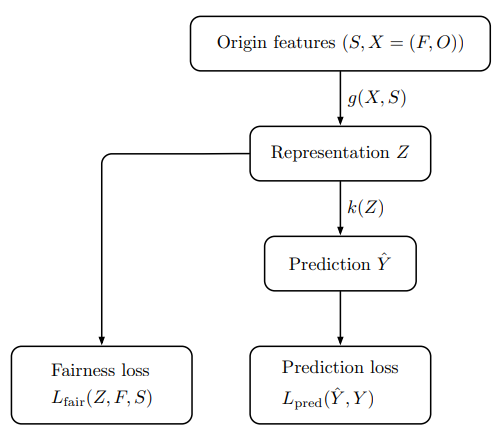
如今，公平问题已经成为了决策系统中的重要问题。已经有很多学者提出了各种公平的概念来衡量算法的不公平程度。Judea Pearl研究了伯克利大学研究生入学性别偏见的案例。数据显示，总体而言，男性申请人的入学率较高，但在研究院系选择时，结果有所不同。由院系选择引起的偏差应该被认为是公平的，但传统的群体公平观念由于没有考虑院系选择而无法判断公平。受此启发，基于因果关系的公平理念应运而生。在这些论文中，作者首先假设了特征之间的因果图，然后，他们可以将敏感属性对结果的不公平因果效应定义为一个度量。然而，这些公平性概念需要非常有力的假设，而且它们不可扩展。在实践中，经常存在一组我们称之为公平变量的变量，它们是决策前的协变量，例如用户的选择。


公平变量并不会影响评估决策支持算法的公平性。因此，崔鹏老师团队通过设置公平变量将条件公平定义为更合理的公平度量。通过选取不同的公平变量，崔鹏老师团队证明了传统的公平概念，例如统计公平和机会均等，是条件公平符号的特例。并且提出了一种可求导的条件公平正则化器（Derivable Conditional Fairness Regularizer, DCFR），它可以集成到任何决策模型中，以跟踪算法决策的精度和公平性之间的权衡。

图20：DCFR的框架。

为了公平比较，在实验中，选择也使用对抗性表示学习的方法来解决问题的公平优化算法作对照。有UNFAIR、ALFR、CFAIR和LAFTR，以及它的变体LAFTR-DP和LAFTR-EO。

图21：各种数据集（从上到下依次为收入数据集、荷兰人口普查数据集、COMPAS数据集）上不同公平性指标（从左到右依次为Δ𝐷𝑃、Δ𝐸𝑂、Δ𝐶𝐹）的准确性-公平性权衡曲线。DCFR以粗线显示。

很明显，在实验中DCFR更有优势，在准确性和公平性上达到更好的权衡效果。对于统计公平和机会均等任务，DCFR的退化变体能有与专为这些任务设计的最先进基线方法相当的性能，有时甚至还能有更好的结果。综上所述，DCFR在真实数据集上非常有效，并在条件公平目标上取得了良好的性能。并且随着公平变量的数量增加，其表现会更好。


稳定学习与领域自适应[14]

稳定学习最初的定义是不需要目标域信息的，这里的领域自适应是一种利用了目标域信息的做法，可以理解为拓展了最初的稳定学习的含义。


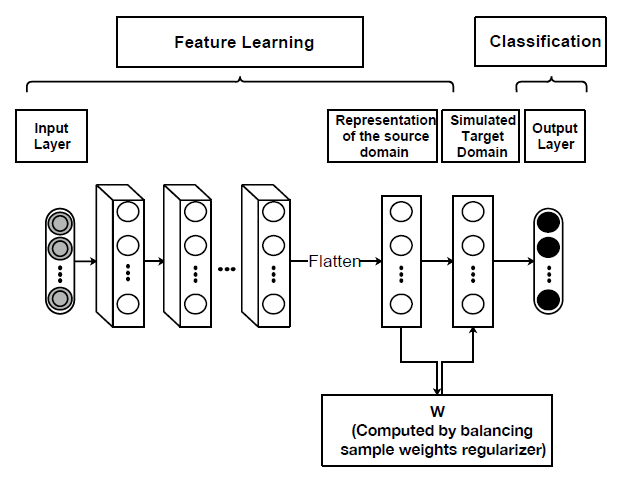
研究表明，深度神经网络学习到的表征可以转移到我们没有充足标记数据的其他领域中，并进行类似的预测任务。然而，当我们过渡到模型中的更高神经层时，表征变得更加适用于特定任务而不通用。关于这个问题，深度域适应的研究提出通过强制深度模型学习更多跨域可迁移的表征来缓解。这其实是通过将域适应方法整合到深度学习管道中来实现的。然而，相关性并不总是可转移的。亚利桑那州立大学（Arizona State University，ASU）刘欢老师团队提出了一个用于无监督域适应 (Deep Causal Representation learning framework for unsupervised Domain Adaptation, DCDAN) 的深度因果表示学习框架，以学习用于目标域预测的可迁移特征表示，如图22所示。其实就是使用来自源域的重新加权样本来模拟虚拟目标域，并估计特征对结果的因果影响。

图22：DCDAN概述。

DCDAN由一个正则化项组成，该正则化项通过平衡从数据中学习到的特征表示的分布来学习源数据的平衡权重。这些权重的设计有助于模型捕捉特征对目标变量的因果影响，而不是它们的相关性。此外，我们的模型包括深度神经网络的加权损失函数，其中每个样本的权重来自正则化项，损失函数负责学习预测域不变特征，以及将学习到的表征映射到输出的分类器或因果机制。将学习组件的样本权重嵌入到模型的管道中，并将这些权重与表征联合学习，这样不仅可以从深度模型中受益，还能学习对目标具有可转移性和良好预测效果的因果特征。

图23：DCDAN生成的数据集中样本示例(EQ2)和热图。图23(a)显示了来自数据的示例图像，图23(b)显示了从VQA-X数据集中提取的图23(a)的因果特征的基本事实，图23(c) 显示了DCDAN为因果表征生成的热图

为了验证该框架的有效性，亚利桑那州立大学（Arizona State University，ASU）刘欢老师团队将ResNet-50、DDC、DAN、Deep CORAL、DANN、HAFN设置为对照方法来进行实验。


图24：DCDAN和Resnet-50 在VQA-X数据子集上生成的热图。
图25：在任务上具有不同超参数、和的DCDAN的准确性。

在实验中，DCDAN在许多情况下优于基线方法，结果表明DCDAN可以执行无监督的域自适应，显示了它在学习因果表示方面的有效性。而且这还验证了因果特征表示有助于学习跨域的可迁移特征，进一步证实了因果损失和分类损失之间的良好权衡可以导致学习更多可转移的特征。

小结

总的来说，稳定学习受到因果推断的启发，试图识别出在不同环境下都具有稳定性的预测变量，从而克服虚假相关带来的影响，使得机器学习模型在不同环境下的表现在理论上具有稳定性。最开始的稳定学习方法改进自因果推断中的协变量平衡，而随后发展的方法还包括了统计学习、优化过程等不同视角，因此进一步丰富了稳定学习的含义。稳定学习为当下机器学习和预测建模提供了一个新的学习范式，来弥补相关性学习和因果关系之间的鸿沟，从而一定程度上克服机器学习模型在稳定性、可解释性和公平性等方面所面临的风险。在未来，稳定学习将继续致力于在不牺牲预测能力的情况下构建更加可信的预测模型，并合理地放松关于因果推断的严格假设，以匹配更多现实的应用场景。


参考文献

  1. ↑ Peng, C. and A. Susan, Stable learning establishes some common ground between causal inference and machine learning. Nature machine intelligence, 2022. 4(2): p. 110-115.
  2. ↑ Kuang, K., et al. Stable Prediction across Unknown Environments. in ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. 2018.
  3. ↑ Shen, Z., et al. Stable Learning via Differentiated Variable Decorrelation. in 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. 2020: ACM.
  4. ↑ Shen, Z., et al., Stable Learning via Sample Reweighting. AAAI2020, 2019.
  5. ↑ Kuang, K., et al. Stable Prediction with Model Misspecification and Agnostic Distribution Shift. in Association for the Advancement of Artificial Intelligence. 2020.
  6. ↑ Liu, J., et al. Stable Adversarial Learning under Distributional Shifts. in Association for the Advancement of Artificial Intelligence, 2021. 2020.
  7. ↑ Liu, J., et al. Heterogeneous Risk Minimization. in International Conference on Machine Learning. 2021.
  8. ↑ Liu, J., et al. Kernelized Heterogeneous Risk Minimization. in 35th Conference on Neural Information Processing Systems (NeurIPS 2021). 2021.
  9. ↑ Xu, R., et al., Why Stable Learning Works? A Theory of Covariate Shift Generalization. 2021.
  10. ↑ He, Y., et al. Learning Stable Graphs from Multiple Environments with Selection Bias. in ACM Conferences. 2020: ACM.
  11. ↑ Zhang, S., et al., Stable Prediction on Graphs with Agnostic Distribution Shift. 2021.
  12. ↑ Zhang, X., et al. Deep Stable Learning for Out-Of-Distribution Generalization. in 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). 2021.
  13. ↑ Xu, R., et al. Algorithmic Decision Making with Conditional Fairness. in ACM Conferences. 2020: ACM.
  14. ↑ Moraffah, R., et al., Deep causal representation learning for unsupervised domain adaptation. 2019.

编辑推荐

以下三篇论文与该主题相关的文章：

  1. He, Y., et al., CausPref: Causal Preference Learning for Out-of-Distribution Recommendation. arXiv.org, 2022.
  2. Zimu Wang, Y.H.J.L., Invariant Preference Learning for General Debiasing in Recommendation. ACM SIGKDD 2022, 2022.
  3. Zheyan Shen, J.L.Y.H., Towards Out-Of-Distribution Generalization：A Survey. Arxiv, 2021.


本中文词条由由集智社区成员东南大学 乔一斯，薄荷编辑，如有问题，欢迎在讨论页面留言。 本词条内容源自wikipedia及公开资料，遵守 CC3.0协议。

[[Category:读书会]

取自“https://wiki.swarma.org/index.php?title=稳定学习&oldid=32921”