后门准则

为何需要后门准则

在结构因果图中，我们往往需要估计变量[math]\displaystyle{ X }[/math]对另一个变量[math]\displaystyle{ Y }[/math]的因果效应，而结构因果图也随着图中节点数量的增加变得异常复杂，进一步加大了因果效应估计的难度。在计算[math]\displaystyle{ X }[/math]对[math]\displaystyle{ Y }[/math]的因果效应时，我们必须保证排除一切存在与变量[math]\displaystyle{ X }[/math]与[math]\displaystyle{ Y }[/math]之间的虚假关系，即非[math]\displaystyle{ X }[/math]对[math]\displaystyle{ Y }[/math]的因果途径，同时保持变量[math]\displaystyle{ X }[/math]与[math]\displaystyle{ Y }[/math]的因果途径完好无缺。换言之，寻找一个条件节点集合[math]\displaystyle{ \mathbf{Z} }[/math]使得能阻断任何含有指向[math]\displaystyle{ X }[/math]的后门路径（指可能使得[math]\displaystyle{ X }[/math]和[math]\displaystyle{ Y }[/math]相关但并不传递X产生的因果效应），因为如果不阻断这些后门路径，它们会混淆[math]\displaystyle{ X }[/math]对[math]\displaystyle{ Y }[/math]的因果效应。而后门准则就是用于快速寻找节点集合[math]\displaystyle{ \mathbf{Z} }[/math]的有效判断准则，是结构因果图在实际应用中使用最广泛的基础准则之一。

定义

给定有向无环图中的一对有序变量[math]\displaystyle{ (X,Y) }[/math]，如果变量集合[math]\displaystyle{ \mathbf{Z} }[/math]满足：

[math]\displaystyle{ \mathbf{Z} }[/math]中没有[math]\displaystyle{ X }[/math]的后代节点；
[math]\displaystyle{ \mathbf{Z} }[/math]阻断了[math]\displaystyle{ X }[/math]与[math]\displaystyle{ Y }[/math]之间的每条[math]\displaystyle{ X }[/math]的后门路径和伪路径，则称[math]\displaystyle{ \mathbf{Z} }[/math]满足关于[math]\displaystyle{ (X,Y) }[/math]的后门准则。

注意：有序变量[math]\displaystyle{ (X,Y) }[/math]的后门路径指在变量[math]\displaystyle{ X }[/math]和[math]\displaystyle{ Y }[/math]之间的任何指向[math]\displaystyle{ X }[/math]的路径，而伪路径指所有其他既不是[math]\displaystyle{ X }[/math]指向[math]\displaystyle{ Y }[/math]的因果路径、也不是指向[math]\displaystyle{ X }[/math]的后门路径、但会连通变量[math]\displaystyle{ X }[/math]与[math]\displaystyle{ Y }[/math]的其他路径，如图2中的以变量[math]\displaystyle{ W }[/math]为条件打开的[math]\displaystyle{ X\rightarrow W \leftarrow Z\leftarrow T\rightarrow Y }[/math]路径。

第一个条件是为了确保条件节点集合不能包含变量[math]\displaystyle{ X }[/math]的后代节点，因为在进行评估[math]\displaystyle{ X }[/math]对变量[math]\displaystyle{ Y }[/math]的因果效应时，会对变量[math]\displaystyle{ X }[/math]采取干预，继而影响变量[math]\displaystyle{ X }[/math]的后代节点，从而影响变量[math]\displaystyle{ Y }[/math]，但以[math]\displaystyle{ X }[/math]的后代节点为条件会阻断这些路径。第二个条件是为了阻断所有一切伪路径以及条件节点集合引入的新伪路径。

如果变量集合[math]\displaystyle{ \mathbf{Z} }[/math]满足[math]\displaystyle{ (X,Y) }[/math]的后门准则，那么[math]\displaystyle{ X }[/math]对[math]\displaystyle{ Y }[/math]的因果效应可以对变量集[math]\displaystyle{ \mathbf{Z} }[/math]的校正得到，即对[math]\displaystyle{ \mathbf{Z} }[/math]中所有变量进行概率求和，具体计算如下：

[math]\displaystyle{ P(Y=y|do(X=x)) = \sum_zP(Y=y|X=x, \mathbf{Z}=z)P(\mathbf{Z}=z) }[/math]

后门准则实例

实例1

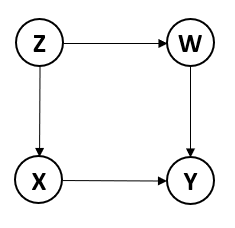
图1：[math]\displaystyle{ X }[/math]：新药；[math]\displaystyle{ Y }[/math]:痊愈率；[math]\displaystyle{ W }[/math]:体重；[math]\displaystyle{ Z }[/math]:经济社会地位

试图获取药物[math]\displaystyle{ X }[/math]对痊愈率[math]\displaystyle{ Y }[/math]的因果效应，同时还测量了对痊愈率有影响的体重[math]\displaystyle{ W }[/math]。另外，我们知道经济社会地位[math]\displaystyle{ Z }[/math]同时影响患者体重和患者对接受治疗的选择，但是在这个研究中并没有关于经济社会地位的统计数据。

在图1的因果图中包含四个变量[math]\displaystyle{ X }[/math]、[math]\displaystyle{ Y }[/math]、[math]\displaystyle{ W }[/math]、[math]\displaystyle{ Z }[/math]四个变量，现在我们估计变量[math]\displaystyle{ X }[/math]对变量[math]\displaystyle{ Y }[/math]的因果效应，即搜索满足有向变量对[math]\displaystyle{ (X，Y) }[/math]的后门准则的变量集合。不难发现，节点[math]\displaystyle{ W }[/math]（非[math]\displaystyle{ X }[/math]的后代）阻断了指向[math]\displaystyle{ X }[/math]的后门路径[math]\displaystyle{ X\leftarrow Z \rightarrow W \rightarrow Y }[/math]，但没有创造新的后门路径或者改变从[math]\displaystyle{ X }[/math]到变量[math]\displaystyle{ Y }[/math]的有向路径，因此单个节点[math]\displaystyle{ W }[/math]满足后门准则，因此，只要校正[math]\displaystyle{ W }[/math]就能得到从变量[math]\displaystyle{ X }[/math]到变量[math]\displaystyle{ Y }[/math]的因果效应，即

[math]\displaystyle{ P(Y=y|do(X=x)) = \sum_wP(Y=y|X=x, W=w)P(W=w) }[/math]

实例2

在寻找满足后门准则的节点集合时，需要特别关注对撞节点。

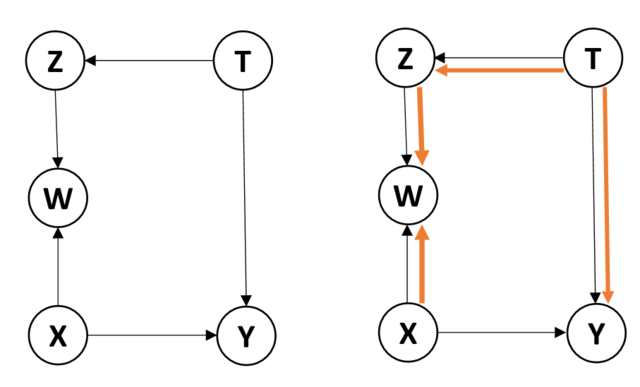
图2：基于对撞节点[math]\displaystyle{ W }[/math]的[math]\displaystyle{ w }[/math]-特定因果效应[math]\displaystyle{ P(y|do(x),w) }[/math]的因果图

在图2中，当节点集合为空集时，没有存在从[math]\displaystyle{ Y }[/math]到[math]\displaystyle{ X }[/math]的后门路径。但是，如果节点集合中包含对撞节点[math]\displaystyle{ W }[/math]，则打开了路径[math]\displaystyle{ X\rightarrow W \leftarrow Z\leftarrow T\rightarrow Y }[/math]（图中黄色路径），该路径不是从[math]\displaystyle{ X }[/math]到[math]\displaystyle{ Y }[/math]的因果路径也不是后门路径，但是伪路径，打开这条路径会产生偏差并导致错误的估计。这也意味着，对[math]\displaystyle{ W }[/math]的每个值分别计算[math]\displaystyle{ X }[/math]和[math]\displaystyle{ Y }[/math]的关联性，不会得到[math]\displaystyle{ X }[/math]对[math]\displaystyle{ Y }[/math]的因果效应，甚至对于[math]\displaystyle{ W }[/math]的每个值计算[math]\displaystyle{ X }[/math]和[math]\displaystyle{ Y }[/math]的关联性也是错误的。

那么，当指定[math]\displaystyle{ W }[/math]为一个确定值[math]\displaystyle{ w }[/math]时，如何计算[math]\displaystyle{ X }[/math]对[math]\displaystyle{ Y }[/math]的因果效应？解决方法是选择其他变量来阻断由[math]\displaystyle{ W }[/math]打开的路径。例如，选择变量[math]\displaystyle{ T }[/math]为条件，仍可阻断[math]\displaystyle{ X\rightarrow W \leftarrow Z\leftarrow T\rightarrow Y }[/math]，因此，为了计算[math]\displaystyle{ w }[/math]-特定因果效应[math]\displaystyle{ P(y|do(x),w) }[/math]，可以对变量[math]\displaystyle{ T }[/math]进行校正：

[math]\displaystyle{ P(Y=y|do(X=x)， W=w) = \sum_tP(Y=y|X=x, W=w,T=t)P(T=t|X=x, W=w) }[/math]

[math]\displaystyle{ w }[/math]-特定因果效应[math]\displaystyle{ P(y|do(x),w) }[/math]表明[math]\displaystyle{ X }[/math]对[math]\displaystyle{ Y }[/math]的因果效应依据[math]\displaystyle{ W }[/math]值的变化而改变。

实例3

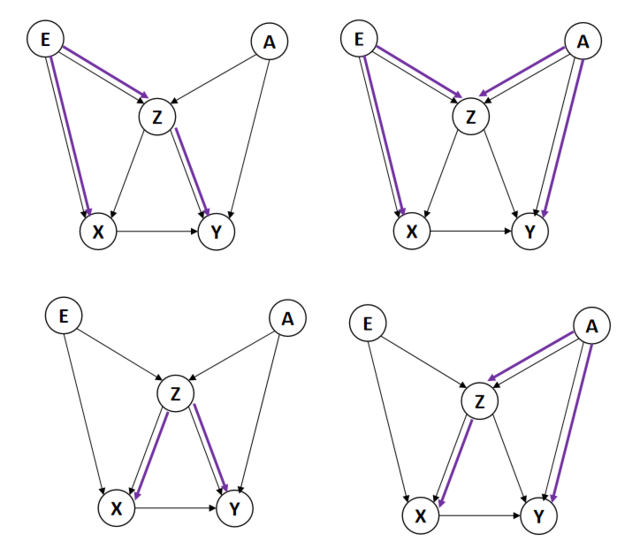
在某些因果图中，校正对撞节点有时候是不可避免的，如图3所示。

图3：必须校正对撞节点[math]\displaystyle{ Z }[/math]的因果图

在图3中，从[math]\displaystyle{ X }[/math]到[math]\displaystyle{ Y }[/math]有四条后门路径（图中紫色路径），而且都经过[math]\displaystyle{ Z }[/math]节点。在路径[math]\displaystyle{ X\leftarrow E \rightarrow Z \leftarrow A \rightarrow Y }[/math]中，变量[math]\displaystyle{ Z }[/math]节点是一个对撞节点，以[math]\displaystyle{ Z }[/math]为条件会导致这条路径联通。因此，要阻断所有四条后门路径，可以选择包含变量[math]\displaystyle{ Z }[/math]的变量集合，如[math]\displaystyle{ \{Z,A \} }[/math]、[math]\displaystyle{ \{Z,E \} }[/math]、[math]\displaystyle{ \{Z,A,E \} }[/math]。

实例4 - 辛普森悖论

图4：[math]\displaystyle{ X }[/math]：代表药物；[math]\displaystyle{ Y }[/math]:痊愈；[math]\displaystyle{ Z }[/math]:性别

为了确定药物在人群中的有效性，设想一种假设性的干预措施，即对整个人群统一服用这种药物，并与补充干预下的痊愈率进行比较，补充干预指阻止每个人服用药物。用[math]\displaystyle{ do(X=1) }[/math]表示第一种干预，用[math]\displaystyle{ do(X=0) }[/math]表示第二种干预，现在要估计它们的差异：

[math]\displaystyle{ P(Y=y|do(X=1)) - P(Y=y|do(X=0)) }[/math]

在没有因果关联的情况下，无法从数据集本身估计因果效应，这就是辛普森悖论的教训，数据本身甚至不足以确定药物的作用是正面的还是负面的。但是借助图4的因果图模型，可以从数据中计算因果效应的大小。为此，以对图进行处理的形式模拟干预，即对模型中全体人群都服用了该药物。

表1.1 一种新药临床试验对比（考虑性别因素）
	患者服药情况		患者未服药情况
患者	痊愈患者数	痊愈率/%	痊愈患者数	痊愈率/%
男性患者	81例 (共87例)	93	234例 (共270例)	87
女性患者	192例 (共263例)	73	55例 (共80例)	69
合计	273例 (共350例)	78	289例 (共350例)	83

[math]\displaystyle{ \begin{alignat}{3} P(Y=1|do(X=1)) & = \sum_Z P(Y=1|X=1, Z=z)P(Z) \\ & = P(Y=1|X=1, Z=1)P(Z=1) + P(Y=1|X=1, Z=0)P(Z=0) \\ &= \frac{0.93*(87+270)}{700} + \frac{0.73*(263+80)}{700} = 0.832 \\ \end{alignat} }[/math]

同理，

[math]\displaystyle{ \begin{alignat}{3} P(Y=1|do(X=0)) & = \sum_Z P(Y=1|X=0, Z=z)P(Z) \\ & = P(Y=1|X=0, Z=1)P(Z=1) + P(Y=1|X=0, Z=0)P(Z=0) \\ & = \frac{0.87*(87+270)}{700} + \frac{0.69*(263+80)}{700} = 0.781 \end{alignat} }[/math]

因此，服用药物的效果和不服用药物的效果的差异为：

[math]\displaystyle{ \begin{alignat}{3} P(Y=1|do(X=1)) - P(Y=1|do(X=0)) & = 0.832 - 0.781 \\ & = 0.0502 \end{alignat} }[/math]

参考文献

Judea Pearl,Madelyn Glymour, Nicholas P. Jewell. Causal Inference in Statistics: A Primer

编者推荐

书籍推荐

《统计因果推理入门》封面

统计因果推理入门对应英文Causal Inference in Statistics: A Primer

这本书非常适合初学者入门因果科学，这里面涉及到对结构因果模型的详细定义和阐述，非常清晰易懂。

为什么-关于因果的新科学

《为什么-关于因果关系的新科学》封面

在本书中，人工智能领域的权威专家朱迪亚·珀尔及其同事领导的因果关系革命突破多年的迷雾，厘清了知识的本质，确立了因果关系研究在科学探索中的核心地位。

关于这本书集智俱乐部邀请白楚研究员用100分钟，为大家详细介绍了Judea Pearl绘制的因果科学蓝图，作为一个起点，去拥抱因果革命。可以查看对应的视频分享解读《为什么》：攀登因果之梯

课程推荐

基于后门调整的因果推荐系统 | 第二季第十二期

这个视频邀请新加坡国立大学研究员冯福利老师介绍如何有效地将因果理论引入数据驱动的推荐模型，主要介绍通过引入后门调整处理：1）流行度偏差；2）用户兴趣放大。

因果科学与 Causal AI 系列读书会

图灵奖得主朱迪亚·珀尔教授认为，当下正在进行一场改变数据科学的新革命 ”因果革命“。它以科学为中心，涉及从数据到政策、可解释性、机制的泛化，再到一些社会科学中的归因和公平性问题，甚至哲学中的创造性和自由意志。本季读书会以Elements of Causal Inference一书为线索，主要展现因果科学在机器学习各个方向上的影响，包括强化学习、迁移学习、表示学习等等，并分享在工业界的部分应用成果。本季读书会梳理了因果科学的核心内容，理解它如何改变数据科学，助力 AI 系统超越曲线拟合和获得回答因果问题的能力。

因果科学与Causal AI读书会第二季

因果推断与机器学习领域的结合已经吸引了越来越多来自学界业界的关注。第一季读书会主要关注了因果科学在机器学习方向上的前沿应用，为深入探讨、普及推广因果科学议题，第二季读书会着力于实操性、基础性，带领大家精读因果科学方向两本非常受广泛认可的入门教材：Causal inference in statistics: A primer和Elements of causal inference: foundations and learning algorithms。读书会以直播讨论为主，结合习题交流、夜谈、编程实践、前沿讲座等多类型内容，主要面向有机器学习背景、希望深入学习因果科学基础知识和重要模型方法、寻求解决相关研究问题的研究人员。

因果科学读书会第三季：因果+X

“因果”并不是一个新概念，而是一个已经在多个学科中使用了数十年的分析技术。通过前两季的分享，我们主要梳理了因果科学在计算机领域的前沿进展。如要融会贯通，我们需要回顾数十年来在社会学、经济学、医学、生物学等多个领域中，都是使用了什么样的因果模型、以什么样的范式、解决了什么样的问题。我们还要尝试进行对比和创新，看能否以现在的眼光，用其他的模型，为这些研究提供新的解决思路。

“因果+X”就是要让因果真正地应用于我们的科学研究中，不管你是来自计算机、数理统计领域，还是社会学、经济学、管理学领域，还是医学、生物学领域，我们希望共同探究出因果研究的范式，真正解决因果的多学科应用问题，乃至解决工业界的问题。