倾向评分
倾向评分定义为给定协变量后个体接受处理的概率。倾向评分是平衡得分,亦即对于倾向评分相同的个体,协变量分布在处理组和对照组间是平衡的。
定义
记X为协变量,W为处理变量,倾向得分(Propensity score)定义为
[math]\displaystyle{ e(x)=P(W=1|X=x) }[/math]
性质
给定倾向得分e(X)的值,协变量分布在处理组和对照组间是平衡的,即倾向得分是平衡得分:
[math]\displaystyle{ X \perp W|e(X) }[/math]
记Y(w)为处理w对应的潜在结果,Y为观测到的结局,那么在无混淆性假设[math]\displaystyle{ W \perp (Y(1),Y(0))|X }[/math]下,有
[math]\displaystyle{ W \perp (Y(1),Y(0))|e(X) }[/math]
因此,只要给定了倾向得分,潜在结果就和处理变量独立。为了估计平均因果作用,不需要控制所有的协变量,而只需要控制倾向得分。
倾向得分的估计
最常见的倾向得分估计方法是逻辑斯谛回归,
[math]\displaystyle{ e(x) =\frac{exp(X\beta )}{1+exp(X\beta )} }[/math]
可由广义线性模型估出。此外,可利用非参数估计,如核估计、局部线性回归。
在用逆概率加权方法估计平均因果作用时,利用了倾向得分的平衡得分性质。因此,逆概率加权估计的准确性主要受制于倾向得分能否很好地平衡协变量,而倾向得分本身估计的准确性并不会对平均因果作用估计的准确性造成直接影响。为了检验倾向得分是否能较好地平衡协变量,可以按照倾向得分的估计值对样本分成k层(0=b_0<b_1<⋯<b_k=1),检验每一层内处理组和对照组的协变量分布是否平衡,或检验在每一层内
[math]\displaystyle{ E\left [ W|X, b_{j-1} \lt \hat{e(X)} \leq b_{j}\right ]=E\left [ W| b_{j-1} \lt \hat{e(X)} \leq b_{j}\right ] }[/math]
亦即检验每一层内W对X回归系数为0。
在有限样本特别是低维协变量的情形中,为了达到倾向得分的平衡得分性质,可通过求解
[math]\displaystyle{ \sum_{i=1}^{n}\frac{W_{I}}{e(X_{i})}X_{i}=\sum_{i=1}^{n}X_{i} }[/math]
从而估计倾向得分。
倾向得分匹配的步骤
对于倾向性得分相同的一群用户,treatment 和特征是独立的,treatment 和潜在结果也是独立的。
因此,理论上,如果我们对每一个实验组用户都在对照组里匹配一个得分相等(要求有点严苛)的用户,我们就能得到同质的实验组和对照组,就可以假装我们做了一个 A/B Test 了,接着就可以随意地进行组间比较了。
具体步骤为:
倾向性得分估算
按需做一下特征预处理,套用公式进行计算,如果发现某些变量匹配效果不好,可以考虑加入一些高阶项,重来一遍。
倾向性得分匹配:怎么匹配?
假设我们已经有了每个用户的倾向性得分,我们的目标是针对目前的实验组用户,匹配得到一个近乎于同质的对照组。
当用户量足够时候,一个简单做法是进行一对一无放回匹配:对于每一个实验组用户,我们去对照组里找一个倾向性得分最近的用户,把他们配成一对。匹配过程中,可以限制一下配对用户的得分差异不能超过某一个阈值,配不上就算了,以防把 “太不相似” 的用户匹配在一起。
在实现匹配时,有很多选项与细节。和机器学习里调每个参数都对应着某些 trade-off 类似,每个选项背后也都有对应的 bias-variance 的 trade-off 的。
匹配用的得分:
可选原始倾向性得分 e (x)或者得分的 logit;
l (x)=ln (e (x)/(1-e (x))) ,接下来都统一用e表示。
修剪(trimming):
可以先筛选掉倾向性得分比较 “极端” 的用户,例如在现实中不大可能出现在实验组里的对照组用户。常见的做法是保留得分在[ e_{min}, e_{max} ]这个区间的用户,关于区间选择,下面是两个例子。
- 实验组和对照组用户得分区间的交集
- 只保留区间中部 90% 或者 95%,如取原始得分在[0.05,0.95]的用户
匹配(matching):
实验组对对照组根据得分进行匹配时候,比较常见的有以下两种方法。
- nearest neighbors: 进行 1 对 K 有放回或无放回匹配
- radius: 对每个实验组用户,匹配上所有得分差异小于指定 radius 的用户
得分差异上限(caliper):当我们匹配用户的时候,我们要求每一对用户的得分差异不超过指定的 caliper
通过短短几行的代码,配平一下经典数据集 NSW-Data-Obs。
MatchIt 会帮我们估算好倾向性得分,再进行匹配。
set.seed(42)
m.out <- matchit(data = nsw_data_obs,
formula = treat ~ age + I(age^2) + I(age^3) + educ + black + hispan + married +
I(re74/1000) + I(re75/1000),
method = "nearest",
distance = "logit",
replace = FALSE,
caliper = 0.05)平衡性检查:怎么量化匹配效果?
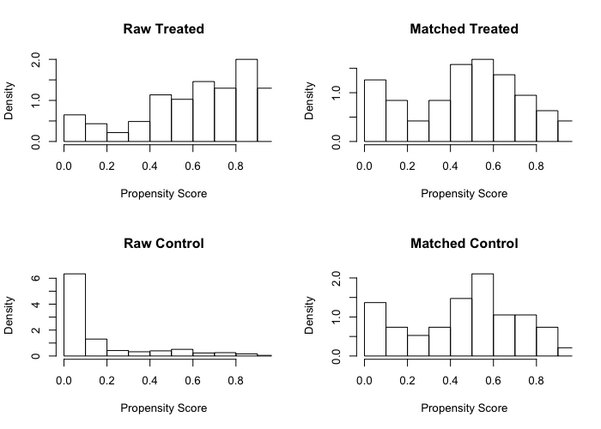
看倾向性得分在匹配前后的分布、以及特征在匹配前后的 QQ-Plot来比较直观的衡量“配平效果 “
- 因果效应估算:怎么从匹配后的两组用户中得到因果效应?
- 敏感度分析:分析结论对于混淆变量选没选对(不满足 unconfoundedness )是不是很敏感?
MatchIt 自带这些功能,具体代码为:
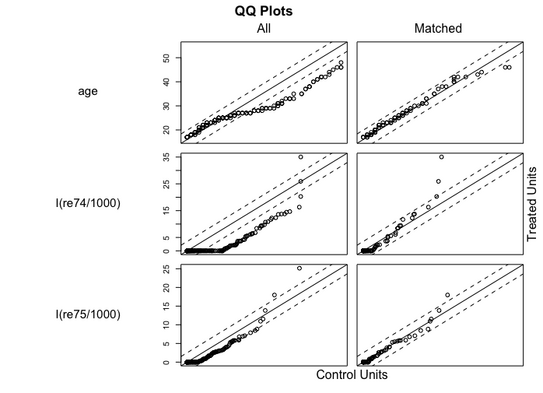
plot(m.out, type = "hist", interactive = F)
plot(m.out, type = "QQ", interactive = F, which.xs = c("age", "I(re74/1000)", "I(re75/1000)"))下面两张图里是 NSW-Data-Obs 的配平结果。
可以看出,匹配后的实验组和对照组的倾向性得分分布更加接近,变量分布也更接近。
此外,通过Coursera 上的公开课 “A Crash Course in Causality: Inferring Causal Effects from Observational Data” 里介绍的量化配平效果的指标 Standarized Mean Difference (SMD)。
SMD =(实验组均值 - 对照组均值)/ 实验组标准差。
如果一个变量的 SMD 不超过 0.1,一般就可以认为这个变量的配平质量可以接受。
当一个变量的 SMD 超过 0.1 的时候,需要凭经验确认一下那个变量是不是没有那么重要。
MatchIt 里自带函数,可以计算配平前后每个变量的各类统计结果,其中也包括了 SMD。
因果效应推断
因果效应的推断即推断 ATT (Average Treatment Effect on the Treated)。
ATT=E [Y_1 - Y_0 | T=1]
有很多方法可以用来估算 ATT 。
1.直接比较匹配后的实验组和对照组
2.拟合一个由干预和用户特征预测观察结果的线形模型,看看干预 T 的系数是多少
对于方法2,对应的代码示例为:
m.data <- match.data(m.out)
# Direct compare
res <- wtd.t.test(m.data$re78[m.data$treat == 1],
m.data$re78[m.data$treat == 0],
weight = m.data$weights[m.data$treat == 1],
weighty = m.data$weights[m.data$treat == 0])
print(res)
mu <- res$additional[1]
std <- res$additional[4]
cat("Confidence interval: ", sapply(qt(c(0.025, 0.975), coef(res)["df"]), function(x){return(mu+x*std)}), "\n")
# Fit
att.fml <- re78 ~ treat + age + educ + black + hispan + married + nodegree + re74 + re75
fit <- lm(att.fml, data = m.data, weights = m.data$weights)
summary(fit)
cat("Confidence interval: ", confint(fit, "treat", 0.95), "\n")敏感性检查
敏感性分析独立于倾向性得分匹配的。主要的目标是衡量当混淆变量(特征)不满足无混杂性时,分析结论是不是稳健的。
一个简单的做法是去掉一个或者多个混淆变量并重复上面的过程,如果分析结论发生很大的改变,说明无混杂性要么依赖于所有特征,要么不成立。
利用倾向得分估计平均因果作用
——逆概率加权估计
在无混淆性假设下,平均因果作用的逆概率加权(Inverse probability weighting)利用了倾向得分:
[math]\displaystyle{ E\left [ Y(1)-Y(0) \right ]=E\left [ \frac{WY}{e(X)} \right ]-E\left [ \frac{1-WY}{1-e(X)} \right ] }[/math]
为了保证上式定义,需要倾向得分满足[math]\displaystyle{ 0\lt e(X)\lt 1 }[/math]。否则,需要截断(Trimming),只保留倾向得分远离0或1的样本,但由于截断后估计平均因果作用时只使用了一部分样本,因此截断后的估计并不是真正的因果作用。如果有n个样本,并且有倾向得分的估计[math]\displaystyle{ \hat{e(x)} }[/math],平均因果作用的逆概率加权估计量可由
[math]\displaystyle{ \sum_{i=1}^{n}\left [ \frac{W_{i}Y_{i}}{\hat{e(X_{i})}}-\frac{(1-W_{i})Y_{i}}{1-\hat{e(X_{i})}} \right ] }[/math]
给出。
类似地,处理组上的平均因果作用
[math]\displaystyle{ E[Y(1)-Y(0)|W=1]=E[WY]-E\left [ e(X)\frac{(1-W)Y}{1-e(X)} \right ] }[/math]
对照组上的平均因果作用
[math]\displaystyle{ E[Y(1)-Y(0)|W=1]=E\left [(1-e(X))\frac{WY}{e(X)} \right ]-E[(1-W)Y)] }[/math]
——子分类估计
子分类(Subclassification)估计按照倾向得分分层,在每一层内估计平均因果作用
[math]\displaystyle{ \hat{\tau _{j}}=\frac{\sum_{i=1}^{n}W_{i}Y_{i}1\left \{b_{j-1}\lt \hat{e(X_{i})}\leq b_{j} \right \}}{\sum_{i=1}^{n}W_{i}1\left \{b_{j-1}\lt \hat{e(X_{i})}\leq b_{j} \right \}}-\frac{\sum_{i=1}^{n}(1-W_{i})Y_{i}1\left \{b_{j-1}\lt \hat{e(X_{i})}\leq b_{j} \right \}}{\sum_{i=1}^{n}(1-W_{i})1\left \{b_{j-1}\lt \hat{e(X_{i})}\leq b_{j} \right \}} }[/math]
记
[math]\displaystyle{ n_{j}=\sum_{i=1}^{n}1\left \{b_{j-1}\lt \hat{e(X_{i})}\leq b_{j} \right \} }[/math]
于是平均因果作用的子分配估计为
[math]\displaystyle{ \hat\tau _{j}=\sum_{j=1}^{k}\frac{\hat{n_{j}}}{n}\tau _{j} }[/math]
可以看出,子分类估计实际上在每一层内使用了常数的倾向得分
[math]\displaystyle{ \hat{e(x)}=\frac{\sum_{i=1}^{n}W_{i}1\left \{b_{j-1}\lt \hat{e(X_{i})}\leq b_{j} \right \}}{\sum_{i=1}^{n}1\left \{b_{j-1}\lt \hat{e(X_{i})}\leq b_{j} \right \}} }[/math]
常数化的倾向得分能在一定程度上抵抗倾向得分模型设定错误所导致的偏倚,通常子分类估计比逆概率加权估计更稳健
编辑推荐
书籍推荐
关于因果的讨论很多,但是许多入门的教材只是为没有统计学基础的读者介绍如何使用统计学技术处理因果性问题,而没有讨论因果模型和因果参数,本书希望协助具有基础统计学知识的教师和学生应对几乎在所有自然科学和社会科学非试验研究中存在的因果性问题。本书聚焦于用简单和自然的方法定义因果参数,并且说明在观察研究中,哪些假设对于估计参数是必要的。我们也证明这些假设可以用显而易见的数学形式描述出来,也可以用简单的数学工具将这些假设转化为量化的因果关系,如治疗效果和政策干预,以确定其可检测的内在关系。
课程推荐
- 这个视频内容来自集智俱乐部读书会-因果科学与Causal AI读书会第二季内容的分享,由英国剑桥大学及其学习组博士陆超超详细的阐述了潜在结果模型和结果因果模型,并介绍了两个框架的相互转化规律。
- 1. 讲述因果推断的两大框架:潜在结果模型和结构因果模型,讨论他们各自的优缺点以及他们之间的联系,详细介绍他们之间的转化规律。
- 倾向性匹配得分分析(PSM)的原理 醫學統計學從入門到精通【共28節】 - YouTube26
- Youtube搬运的分享视频,介绍了在医学统计学中应用PSM的原理文章总结
经典数据集
经典综述
- Caliendo M, Kopeinig S. Some practical guidance for the implementation of propensity score matching[J]. Journal of economic surveys, 2008, 22(1): 31-72.
文章总结
相关路径
- 因果科学与Casual AI读书会必读参考文献列表,这个是根据读书会中解读的论文,做的一个分类和筛选,方便大家梳理整个框架和内容。
- 因果推断方法概述,这个路径对因果在哲学方面的探讨,以及因果在机器学习方面应用的分析。
- 因果科学和 Causal AI入门路径,这条路径解释了因果科学是什么以及它的发展脉络。此路径将分为三个部分进行展开,第一部分是因果科学的基本定义及其哲学基础,第二部分是统计领域中的因果推断,第三个部分是机器学习中的因果(Causal AI)。