软科学决策支持系统
本文介绍贺仲雄教授近十年来从事决策科学的研究成果:
钱学森同志指出:“要发展软科学需要支持一下模糊数学。”因此称之为“软决策硬功夫”的SDSS大多数都以模糊数学和AI理论为基础,应用现代科学的理论、方法和手段建立的信息决策支持系统。以下介绍贺仲雄教授及其指导的各属研究生邵正强等人研究的几个主要应用系统。
权重分析系统(WAS)
在多目标决策种,加权求和是求解多目标决策问题最常用,最主要的方法。这就需要一个描述指标相对重要程度的权的估价。指标的权应该是指标在决策中相对重要程度的一种主观评价和客观反映的综合度量。因此,权重具有异向作用。在已有的权重分配方法中,主观贝叶斯法往往难以符合实际要求;层次分析法又易产生循环,不满足传递性公理。为此,我们根据集值统计和模糊区间分析方法,并考虑到专家权重中的“权威质量”,“熟悉度”“自信度”,“知识广度”,“意见偏离度”,“智力集法度”等因素,创立了权重分析系统(WAS)
集值统计是经典统计和模糊统计的拓广,其每次试验所得的是一个概率子集。应用这种方法,我们可以得到第m个指标的n个权重子集,将其投影到坐标轴上,即可得权值的叠加区间(图1所示),然后根据精度要求,将其分为若干等分,并对每个小区间求其置信度,
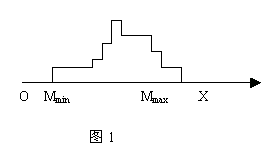
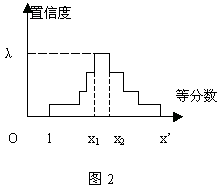
从而得到一置信度序列,反映在置信度坐标轴上如图所示。对图2取λ截集,即得指标m得权重区间值
[x1 ,x2]。
在对此区间数据的处理上,我们采取了三种原则,即最大值的乐观原则;取最小值的悲观原则,以及取均值的平均原则。根据具体的问题,采取以上方法之一,即可得m的权值。
原文: 阎皓 贺仲雄权重分析系统 系统工程与电子技术. 1992,4
国际会议支持系统(MISS)
MISS是近年来各国均在研究的项目,其中很重要的问题即为把会议与内容分别分为若干类,然后对号入座,以便用计算机按标准模式处理,从而节约时间和精力。该问题可抽象为图论中的匹配问题,其性质与m个人,n件工作的分配问题完全相同。图论中的匹配问题只要求“配得上”,对于“配得好”虽有Kuhn—Munkres算法,但考虑的因素太简单。为此我们用模糊集合论作进一步探讨。
多维加权贴近及其约束下的匹配
多维加权贴近度其形式为:
[math]\displaystyle{ (\underline{A},\underline{B})_m = \sum_{i=1}^m \omega_i\delta_i }[/math]
其中[math]\displaystyle{ \underline{A} }[/math] ,[math]\displaystyle{ \underline{B} }[/math]是两个模糊集,m是维数,[math]\displaystyle{ \omega_i }[/math]是第i个指标权重。[math]\displaystyle{ \delta_i }[/math] 是第i个指标的分贴近度,可用距离表示。其最简单的形式就是海明距离。
在m个人,n件工作分配中,设第i个人对工作有若干要求,并构成模糊集[math]\displaystyle{ \underline{A}_i }[/math]
[math]\displaystyle{ \underline{A}_i = (a_{i1}, a_{i2} , ... , a_{ik}) }[/math]
第j个工作岗位对人也有若干要求,也构成模糊集[math]\displaystyle{ \underline{B}_j }[/math]
[math]\displaystyle{ \underline{B}_j = (b_{j1}, b_{j2} , ... , b_{jl}) }[/math]
对这些模糊集合(以模糊向量形式给出)的各个分量加权,这些权数也构成向量ω
[math]\displaystyle{ \omega = (\omega_1, \omega_2, ... , \omega_p) }[/math]
其中 P=max(k,l),且ω由WAS确定。
则匹配隶属度[math]\displaystyle{ \mu_{ij} }[/math]
[math]\displaystyle{ \mu_{ij} = (\underline{A},\underline{B})_p }[/math]
再根据实际需要,预选一阈值M,M∈[0,1] ,可选项在[math]\displaystyle{ \mu_{ij} \ge M }[/math]的一边进行匹配
应用前景
虽然以国际会议支持系统命名,却是一个广义的匹配方法,因此广泛适用于人才调配、物质调运、分配问题、婚姻问题等许多方面,因此应用前景十分广阔。
原文: 贺仲雄等. 国际会议支持系统的一个数学模型:多维加权贴近约束下的匹配问题.系统工程与电子技术. 1987,3
参考文献:贺仲雄等,MIS软件模型——匹配问题的约束与推广 《系统工程理论与实践》1988, (1)
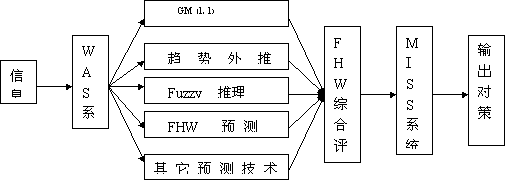
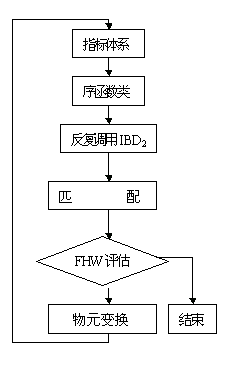
FHW方法
FHW(模糊、灰色、物元空间)方法是贺仲雄教授创立的一种新的决策、评价方法,是对德尔菲法的改进和发展,融合了德尔菲法、BS法(头脑风暴法)、KJ法的优点,并采用了一些新兴学科的思路,如模糊数学、灰色系统理论、物元分析等,从而能定量处理联想思维,而把德尔菲法的咨询表改为FHW咨询表,把向专家咨询的一个数(顺序、判断、打分)改为一个模糊、灰色物元
FHW法的步骤为:
- 收集与指标相关的信息资料,以便能做出判断。
- 填写“FHW评价表”:每个专家填写两次评价表。
第一次,不开讨论会,各自独立思考,充分发挥各自的判断才能,填写A轮评价表。这样 做的目的,是为了使专家在填表时不受“马太效应”的影响。 第二次,召开讨论会,会后再填写B轮表。讨论会上各抒己见,畅所欲言,不要求意见统一。这样可以相互启发,激发联想思维,讨论顺序,一般应和A轮表的填写顺序相反,以防止思维惯性的影响。经过讨论,专家填写B轮表时,尽可能对自己在A轮表中填写的数据作必要的修改。当然,允许不修改自己的意见。
- FHW方法计算各组评价指标。由于每个专家都进行了两轮咨询,所以每个项目都由两个数据,这两个数据便组成一个闭区间,组成模糊灰色物元空间,评价的结果需要得到一个数,所以必须在区间数投影到一个点上,由三种准则可供选择。
第一种,乐观准则。将区间数投影到最大值,这适用于评价条件从宽的情况。
第二种,悲观准则。将区间数投影到最小值,这适用于条件从严掌握的情况。
第三种,平均值准则。将区间数投影到两个端点的平均值。
然后计算主体评分T,总灰色N,白色优劣比S、灰色优劣比D、远近效益En。
其中:T--表示对某组评价指标的基本评价结果。
N--表示对该组指标的朦胧程度,也就是信息不完全程度,N越大可靠性越差。
S--表示当前优势和当前劣势之比,S越大越好。
D--表示潜在优势和潜在列十支笔,D越大越好。
En--表示潜在优势和当前优势之比再乘以系数η,η的具体值需讨论后确定。
这样得到改组评价指标的综合得分:
C=T+S+D+En-N
共适中,T以百分制表示,S、D,En,N一般都不大于一位数。所以,在数据处理过程中,必须对数据进行修正,控制每项数值的范围。
\----摘自《人力资源考评系统》 廖泉文主编 山东人民出版社
该系统86年12月通过国家科委鉴定,被认为在决策方法上具有突破性进展,达到国际水平,其应用案例1992年荣获国家科技进步奖。
FHW问世7年以来,应用效果十分显著,国家科委,中国科协曾先后三次向全国各省市科委系统、中央各部委系统、全国科研单位推广。全国目前已有数百家单位应用FHW系统,已有成果数十项,不少获省、部及国家级奖励。
我们在现有理论与成果的基础上,研制了具有智能决策功能,能处理不相容问题决策和突变预测等多方面实际问题的《扩展FHW系统》软件。
原文:贺仲雄,隋志强. 预测、决策的新方法——模糊灰色物元空间决策系统.系统工程与电子技术. 1986,7:1~11[17]
参考文献:贺仲雄等,FHW专家决策系统计算机实现与专家选择 《系统工程与电子技术》 1987,(1)贺仲雄等,模糊灰色物元空间专家决策系统,北方交通大学学报,1987,(2)
FGR(模糊灰色关联方法)系统
定量测算技术进步对经济增长的影响,是一项十分复杂却有重要意义的工作,也是国际热门课题之一。1928年,美国数学家C.W.cobb和经济学家P.H.Douglas利用美国1899—1922年的统计资料,提出了著名的cobb—Douglas生产函数(简称C—D函数)。但时过60余年,该模型已无法反映当前的宏观、复杂的大系统状态。近年来虽有不少改进,但效果不甚理想。
FGR模型是通过定性分析——统计分析——模糊分析——灰色系统性分析后建立的。它相当于一个“模糊、灰色转换器”,用R表示,
R = α1R1+ α2 R2+ α3 R3
其中:R1 是“灰色关联矩阵”,它在数据充分时起主要作用,其中矩阵元可采用灰色关联度的计算方法得到。 R2是“模糊推理矩阵”,它在数据不够,但经验丰富时起主要作用,其中矩阵元用模糊推理规则得到,R2相当于模糊控制器. R3是C—D矩阵,它具有改进的C—D函数功能。
α1,α2 ,α3 是三个相应矩阵的归一化权重,由WAS确定。
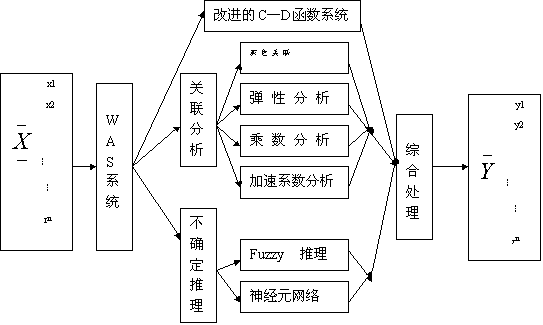
对给出结果可应用FHW、MISS综合处理方法,以得到最佳(优)结果。FGR结构如下:
FGR不仅可对定量指标处理,而且可以处理模糊和灰色指标。这对于解决复杂的预测问题具有强大的魅力。扩展的FGR已从单独的科技进步与经济增长的辖域趋向更广泛的应用世界,它对于经营管理,总体投资,工程判优,工程预测及证券、股票交易都有独到且有价值的帮助。FGR扩展结构如下:
该系统近期通过有关专家鉴定,鉴定认为FGR方法具有国际先进水平,已引起国外有关专家的密切关注。
原文:贺仲雄:测定技术进步对经济增长的模糊、灰色关联方法软件模型. 科学通报. 1991,6
IAD(信息分析决策、对策)系统
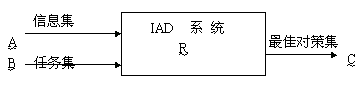
IAD系统是根据决策的一般规律所设计的信息分析决策模型。其主要思路为:
即:输入信息集A和需求集(目标或任务集)B ,通过IAD系统处理,得到最佳对策集 C。其关系如下 :
[math]\displaystyle{ ( \underline{A} \land \underline{B} ) \bullet \underline{R} = \underline{C} }[/math]
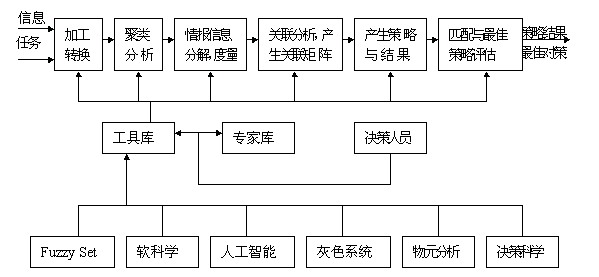
由于宏观、复杂大系统中信息所具有的模糊性、不确定性、不完全性以及不相容等特点,模糊理论、灰色系统、物元分析、知识工程等都成为必不可少的信息分析方法,WAS、MISS、FHW以及FGR也都融于其中,从而形成了一个完整的模糊决策系统,实现了“软硬结合、以软为主”的宏观复杂大系统的决策思想,其结构如下:
由于IAD系统是一个完整的模糊决策体系,其应用前景十分广泛,从军事情报分析,商业经营决策,现代化企业管理,医疗专家会诊直至国家宏观发展战略决策等各个方面。
原文:贺仲雄:情报分析决策系统. 系统工程与电子技术. 1991,11
IBD系统简介
如果说IAD是单方面寻优,那IBD即为多方面最佳寻优方法,其含义为信息协商决策系统。
IBD的主要思想为共同寻优,利益互惠,共同满意原则。与IAD相同,它也属于宏观复杂大系统的决策问题,与IAD的理论基础基本相同。当决策局中人为2时,即IBD2如图7,当局中人为n时,即IBDn,如图8,当局中项为1时,IBD转化为IAD。因此,IBD将广泛适用于工商贸易等经济领域。
原文:贺仲雄、魏小涛. N个剧中人的信息协商决策支持系统(IBDn). 系统工程于电子技术. 1994,3