空间曲面
空间曲面是微分几何中一个非常基础而重要的概念。下面,我们首先以嵌入到三维空间中的曲面为例来进行介绍。
定义
设二维平面([math]\displaystyle{ {\rm I\!R^2} }[/math])上的一个开集为D(如圆形区域或矩形区域),我们设:
[math]\displaystyle{ \textbf{x}: D\rightarrow {\rm I\!R}^3 \qquad (u,v)\mapsto (x^1(u,v),x^2(u,v),x^3(u,v)) }[/math]
来表示一张三维空间的曲面,它是一个D到三维空间的映射。其中,[math]\displaystyle{ x^i(u,v) }[/math]是映射[math]\displaystyle{ \textbf{x} }[/math] 的不同分量。
其中,u和v就是曲面的两个不同参量。我们可以分别为u参数和v参数定义切向量为:
[math]\displaystyle{ \begin{align} &x_u=\left( \frac{\partial{x^1}}{\partial{u}}, \frac{\partial{x^2}}{\partial{u}}, \frac{\partial{x^3}}{\partial{u}}\right)\\ &x_v=\left( \frac{\partial{x^1}}{\partial{v}}, \frac{\partial{x^2}}{\partial{v}}, \frac{\partial{x^3}}{\partial{v}}\right) \end{align} }[/math]
曲面的几何
切平面
如上图所示,如果向量[math]\displaystyle{ \textbf{v}_p }[/math]与曲面M上过p点的某条曲线相切,那么我们就说[math]\displaystyle{ \textbf{v}_p }[/math]与曲面M相切。
切平面定义为所有这样的切向量[math]\displaystyle{ \textbf{v}_p }[/math]所构成的平面[math]\displaystyle{ T_p(M) }[/math]。
当然,这样事先证明所有这样的切向量都在同一张平面上。如果这个条件满足,那么不难知道,该平面的一组基就是[math]\displaystyle{ \{x_u,x_v\} }[/math]。尽管这组基并不相互垂直。
- 定理:一个向量[math]\displaystyle{ \textbf{v} }[/math]在切平面[math]\displaystyle{ T_p(M) }[/math]上的充要条件是它可以写成如下形式:
[math]\displaystyle{ v=\lambda_1 x_u+\lambda_2 x_v }[/math]
证明: (1)首先,证明任何一条M上过p点曲线在该点的切向量都可以写成[math]\displaystyle{ {x_u,x_v} }[/math]的线性表达式。
假设[math]\displaystyle{ \alpha }[/math]是一条曲线,且[math]\displaystyle{ \alpha(0)=p }[/math],并且[math]\displaystyle{ \alpha'(0)=\textbf{v} }[/math]。我们知道,由于曲线在曲面M上,所以[math]\displaystyle{ \alpha(t)=\textbf{x}(u(t),v(t)) }[/math]。这样,由链式求导法则,我们得到[math]\displaystyle{ \alpha'=\frac{\partial \textbf{x}}{\partial u}\frac{du}{dt}+\frac{\partial \textbf{x}}{\partial v}\frac{dv}{dt} }[/math]。所以,[math]\displaystyle{ \alpha(0)=p=\textbf{x}(u(0),v(0)) }[/math]。所以[math]\displaystyle{ u(0)=u_0,v(0)=v_0 }[/math],且:
[math]\displaystyle{ \textbf{v}=\alpha'(0)=\textbf{x}_u(u_0,v_0)\frac{du}{dt}(0)+\textbf{x}_v(u_0,v_0)\frac{dv}{dt}(0) }[/math]
其中,[math]\displaystyle{ \frac{du}{dt}(0),\frac{dv}{dt}(0) }[/math]都可以看作是常数。所以,切向量[math]\displaystyle{ \textbf{v} }[/math]可以看作是向量[math]\displaystyle{ \{\textbf{x}_u,\textbf{x}_v\} }[/math]的线性组合。
(2) 其次,证明,对于任意一组非零常数[math]\displaystyle{ \lambda_1,\lambda_2 }[/math],[math]\displaystyle{ \lambda_1\textbf{x}_u+\lambda_2\textbf{x}_v }[/math]都是某一条曲线[math]\displaystyle{ \alpha(t) }[/math]的切线。
不难构造出这样的曲线为:
[math]\displaystyle{ \alpha(t)=\textbf{x}(u_0+t\lambda_1,v_0+t\lambda_2) }[/math]
那么,它在p点的切向量为:
[math]\displaystyle{ \alpha'(0)=\lambda_1 \textbf{x}_u+\lambda_2 \textbf{x}_v }[/math]
所以,这条曲线的切向量就刚好是我们需要的向量。因此,结论成立。
综合这两条,定理得证。
小结
与曲线的切向量不同,曲面在某一点的切向量有无穷多条,这些切向量构成了一张平面,它是三维空间中的一个特殊的子空间。该平面也是一个线性空间。
法向量
我们定义过点p(其对应的坐标为 [math]\displaystyle{ \textbf{x}(u_0,v_0)=p }[/math])的曲面M的法向量为:
[math]\displaystyle{ N=\textbf{x}_u(u_0,v_0) \times \textbf{x}_v(u_0,v_0) }[/math]
单位法向量自然就是对上述法向量N做归一化处理,即[math]\displaystyle{ U=N/|N| }[/math]。
不难知道,由于切平面上的任意向量都是[math]\displaystyle{ \textbf{x}_u,\textbf{x}_v }[/math]的线性组合,所以法向量N垂直于任意一个向量,所以法向量垂直于整个过p点的切平面[math]\displaystyle{ T_p(M) }[/math]。
几何属性
在微分几何中,我们要考察一张曲面的几何特性,就需要考虑它在一个无穷小空间下的特性。而要想考察这种局部特性,我们需要考虑不同的量(如标量、矢量)沿着曲面进行运动。我们不妨选定一个方向(切向量),然后考察这些量沿着这个切向量是如何运动或改变的。
标量场沿曲面的运动
首先,考虑一个标量场在曲面M上沿着一条曲线[math]\displaystyle{ \alpha(t) }[/math]上的移动,并以此来探测曲面的几何特性。设标量函数[math]\displaystyle{ g(x,y,z) }[/math],并设[math]\displaystyle{ \alpha(t)=(\alpha^1(t),\alpha^2(t),\alpha^3(t)) }[/math]为一条曲线。那么,当我们给参量t一个小的位移dt之后,由于坐标x,y,z都发生了变化,故而标量函数g也会相应地发生变化。这个小变化显然就是对g沿着曲线[math]\displaystyle{ \alpha }[/math]对t求导然后乘以dt,所以,我们不难得到:
[math]\displaystyle{ \begin{align} \frac{d}{dt}(g(\alpha(t)))&=\frac{\partial g}{\partial x} \frac{dx}{dt}+\frac{\partial g}{\partial y} \frac{dy}{dt}+\frac{\partial g}{\partial z} \frac{dz}{dt}\\ &=\frac{\partial g}{\partial x} \frac{d\alpha^1}{dt}+\frac{\partial g}{\partial y} \frac{d\alpha^2}{dt}+\frac{\partial g}{\partial z} \frac{d\alpha^3}{dt}\\ &=\left(\frac{\partial g}{\partial x},\frac{\partial g}{\partial y},\frac{\partial g}{\partial z}\right)\cdot \left(\frac{d\alpha^1}{dt},\frac{d\alpha^1}{dt},\frac{d\alpha^3}{dt}\right)\\ &=\nabla g(\alpha(t))\cdot \alpha'(t) \end{align} }[/math]
其中[math]\displaystyle{ \nabla=\left(\frac{\partial g}{\partial x},\frac{\partial g}{\partial y},\frac{\partial g}{\partial z}\right) }[/math] 为函数g的梯度。
也就是说,标量场沿着曲线运动的改变微量也就体现为标量场在该点的梯度在这个切向量上的投影。
接下来,设任意的切向量[math]\displaystyle{ \textbf{v}\in T_p(M) }[/math],我们考察标量函数沿着这个切向量如何移动。虽然我们说的是g沿着曲面上的切向量v移动,但其实由于v是曲面上的一条曲线[math]\displaystyle{ \alpha(t) }[/math]的函数,所以,也相当于在问这个标量函数沿着曲线的方向如何移动。我们定义g在点p沿着[math]\displaystyle{ \textbf{v} }[/math]方向上的移动称为这个方向上的方向导数。
[math]\displaystyle{ \textbf{v}[g](p)\equiv \frac{d}{dt}(g(\alpha(t)))|_{t=0}=\nabla g(p)\cdot \textbf{v} }[/math]
这里[math]\displaystyle{ \alpha(0)=p\in M }[/math]。
因此,向量[math]\displaystyle{ \textbf{v} }[/math]可以看作是一个函数,它的输入是标量场g,输出是另一个标量场[math]\displaystyle{ \textbf{v}[g]=\nabla g(p)\cdot \textbf{v} }[/math]。
向量场沿曲面运动
下面,我们要考察一个向量场W(x,y,z)沿着一个方向切向量[math]\displaystyle{ \textbf{v} }[/math]运动的时候,向量场如何发生改变。我们知道W可以写为:
[math]\displaystyle{ W=\sum_{i=1}^{3}w^i\textbf{e}_i }[/math]
那么它沿[math]\displaystyle{ \textbf{v} }[/math]的运动显然就是[math]\displaystyle{ \{w^1,w^2,w^3\} }[/math]这三个标量场的运动合成。我们知道这三个标量场的方向导数分别为:[math]\displaystyle{ \{\textbf{v}[w^1],\textbf{v}[w^2],\textbf{v}[w^3]\} }[/math],于是W沿着[math]\displaystyle{ \textbf{v} }[/math]的运动就是一个向量,我们将这个向量定义为向量场W的协变导数
[math]\displaystyle{ \nabla_{\textbf{v}}W\equiv (\textbf{v}[w^1],\textbf{v}[w^2],\textbf{v}[w^3])=\sum_{i=1}^{3}\textbf{v}[w^i]\textbf{e}_i }[/math]
其中,[math]\displaystyle{ \textbf{v}[w^i]=\nabla w^i \cdot \textbf{v} }[/math]
形状算符
以上都是一些数学上的基本准备。下面,我们就来正经研究曲面在一个小区间上的几何属性。如上图,由于曲面上的每个点都对应着一个切平面和法向量,所以要想考察曲面的几何属性,就需要看曲面的法向量如何沿着任意方向移动而发生改变(ΔU)。不难想象得到,法向量的移动本身也构成了一个向量,而这个向量也在该点的切平面里。也就是说,对于不同的切向量,法向量沿着它的运动本身又构成了一个切向量,所以移动就形成了一种将切向量映射为切向量的过程,这就是一个线性的算符,被称为形状算符。因为,这个算符反映了曲面的局域特性。
下面,我们考察一个特殊的向量场,它就是单位法向量U,它沿着任意切向量[math]\displaystyle{ \textbf{v} }[/math]的协变导数为:[math]\displaystyle{ \nabla_{\textbf{v}}U }[/math],它显然可以看成一个关于向量[math]\displaystyle{ \textbf{v} }[/math]的函数。因此,它可以看作是一个算符。
我们将这个关于任意的p点切空间中的向量[math]\displaystyle{ \textbf{v}\in T_p(M) }[/math]的函数称为曲面M在任意点p的形状算符(Shape operator),记为[math]\displaystyle{ S_p }[/math]。
可以证明,[math]\displaystyle{ S_p }[/math]是一个线性空间[math]\displaystyle{ T_p(M) }[/math]上的线性算符。
证明:
首先,要证明[math]\displaystyle{ S_p }[/math]是线性空间[math]\displaystyle{ T_p(M) }[/math]上的合法映射。
即要考察对于任意的[math]\displaystyle{ \textbf{v}\in T_p(M) }[/math],是否有[math]\displaystyle{ S_p(\textbf{v})\in T_p(M) }[/math]。这只需要证明[math]\displaystyle{ S_p(\textbf{v}) }[/math]是与单位法向量U是垂直的就可以了。 我们知道[math]\displaystyle{ U\cdot U=1 }[/math],所以[math]\displaystyle{ 0=\textbf{v}[1]=\textbf{v}[U\cdot U]=2\nabla_{\textbf{v}}U\cdot U }[/math],这就意味着[math]\displaystyle{ \nabla_{\textbf{v}}[U]\cdot U=0 }[/math],也就是[math]\displaystyle{ S_p(\textbf{v}) }[/math]与单位法向量U垂直。
接下来,我们就不难证明对于任意的向量v和w,以及常数a,有(1)[math]\displaystyle{ S_p(a \textbf{v})=a S_p(\textbf{v}) }[/math],(2)[math]\displaystyle{ S_p(\textbf{v}+\textbf{w})=S_p(\textbf{v})+S_p(\textbf{v}) }[/math]。
进一步,由于[math]\displaystyle{ S_p: T_p(M)\rightarrow T_p(M) }[/math]是一个线性映射,所以[math]\displaystyle{ S_p }[/math]就有一个矩阵表示了。于是,我们可以用线性代数的所有工具,例如行列式、迹、特征值等来分析这个算符。
关于形状算符[math]\displaystyle{ S_p }[/math]的一个定理:
定理:形状算符是一个对称的线性变换。并且:
[math]\displaystyle{ \begin{align} &S(\textbf{x}_u)\cdot \textbf{x}_u=\textbf{x}_{uu}\cdot U,\\ &S(\textbf{x}_u)\cdot \textbf{x}_v=\textbf{x}_{uv}\cdot U, \\ &S (\textbf{x}_v)\cdot \textbf{x}_v=\textbf{x}_{vv}\cdot U. \end{align} }[/math]
其中[math]\displaystyle{ \textbf{x}_{uu} }[/math]表示的是[math]\displaystyle{ \textbf{x} }[/math]关于u的二阶导数。
关于形状算符的一种矩阵表示
下面我们以向量组[math]\displaystyle{ \{\textbf{x}_u,\textbf{x}_v\} }[/math]为基,写出形状算符的矩阵表达式如下:
[math]\displaystyle{ \left( \begin{matrix} -\frac{Fm-Gl}{EG-F^2} & \frac{-Fl+Em}{EG-F^2}\\ -\frac{-mG+Fn}{EG-F^2}&\frac{En-Fm}{EG-F^2}\\ \end{matrix} \right) }[/math]
其中, [math]\displaystyle{ E=\textbf{x}_u\cdot \textbf{x}_u, F=\textbf{x}_u\cdot \textbf{x}_v, G=\textbf{x}_v\cdot \textbf{x}_v }[/math]
[math]\displaystyle{ l=S(\textbf{x}_u)\cdot \textbf{x}_u, m=S(\textbf{x}_u)\cdot \textbf{x}_v=S(\textbf{x}_v)\cdot \textbf{x}_u, n=S(\textbf{x}_v)\cdot \textbf{x}_v }[/math]
当这两个基是单位向量的时候,这个矩阵是对称的。
曲面的曲率
我们定义曲面沿着任意一条单位切向量[math]\displaystyle{ \textbf{u}\in T_p(M) }[/math]上的常规曲率(normal curvature)为:
[math]\displaystyle{ \kappa(\textbf{u})=S_p(\textbf{u})\cdot \textbf{u} }[/math]
可以证明,如果[math]\displaystyle{ \alpha }[/math]为一条满足[math]\displaystyle{ \alpha(0)=p,\alpha'(0)=\textbf{u} }[/math]的常速度曲线,那么:
[math]\displaystyle{ \kappa(\textbf{u})=\kappa(0)\cos(\theta) }[/math]
其中[math]\displaystyle{ \kappa(0) }[/math]为曲线在t=0处的曲率,[math]\displaystyle{ \theta }[/math]为曲线上的法向量[math]\displaystyle{ N(0) }[/math]和曲面的法向量[math]\displaystyle{ U(p) }[/math]的夹角。
在所有过点p的切向量[math]\displaystyle{ \textbf{u} }[/math]中,最大的曲率和最小的曲率被称为主曲率(principle curvature)。
高斯曲率
不难看出,[math]\displaystyle{ \kappa(\textbf{u}) }[/math]是一个依赖于切向量[math]\displaystyle{ \textbf{u} }[/math]的量。我们需要定义一个与切向量无关的曲率。
假设S是曲面M的形状算符,那么曲面M在p点的高斯曲率定义为
[math]\displaystyle{ \Kappa(p)=\det(S_p) }[/math]
其中,det表示行列式。与此类似的,M在p点的平均曲率定义为:
[math]\displaystyle{ H(p)=\frac{1}{2}Tr(S_p) }[/math]
其中Tr表示求迹运算。
测地线
我们知道在欧氏空间中,直线是连接两点最短的曲线;与此相对应的是,在球面上,连接两点最短的曲线是大圆。一般地,我们用测地线(Geodesics)来称呼直线在曲面几何中的对应物。但是,我们并不能用两点之间的最短距离来定义这条测地线,原因是这个定义操作性太差,我们需要计算曲线的距离,还需要求解泛函极值。我们需要寻求其它的定义方式。
如图,其中红色的向量为曲面的法向量,绿色的为任意一条曲线α(t)的法向量。对于测地线来说,这两者就应该是重合在一起的。
通常情况下, 人们用二阶导数为零作为条件来定义测地线。具体地,考虑一张曲面M,在其上有一条弧长参数化曲线[math]\displaystyle{ \alpha(t) }[/math](参见空间曲线),那么它在p点的切向量为[math]\displaystyle{ T=\alpha' }[/math],曲线的二阶导数为[math]\displaystyle{ \alpha'' }[/math],也称为曲线的加速度。下面我们将这个加速度沿着T,曲面的发向量U,以及与这二者都垂直的向量[math]\displaystyle{ U\times T }[/math]进行分解有:
[math]\displaystyle{ \alpha''=AT+B(U\times T)+CU }[/math]
其中[math]\displaystyle{ A=\alpha''\cdot T }[/math],可以证明它等于0。
[math]\displaystyle{ B=\alpha''\cdot (U\times T) }[/math],
[math]\displaystyle{ C=\alpha''\cdot U }[/math]
进一步,我们可以对B进行计算:
[math]\displaystyle{ B=U\cdot \alpha'\times \alpha''=|U||\alpha'\times \alpha''|\cos\theta=|T\times T'|\cos\theta=\kappa_{\alpha}\cos\theta }[/math]
其中,[math]\displaystyle{ \kappa_{\alpha} }[/math]刚好是曲线[math]\displaystyle{ \alpha }[/math]在p点的曲率。这最后一步推理是根据[math]\displaystyle{ \alpha }[/math]是弧长参数化曲线,所以|T|=1,于是[math]\displaystyle{ |T\times T'|=|T|\cdot |T'|\sin(\pi/2)=|T'|=\kappa_{\alpha} }[/math]。
而公式中的[math]\displaystyle{ \theta }[/math]为向量[math]\displaystyle{ T\times T' }[/math]与平面的法向量U的夹角。
我们称[math]\displaystyle{ \kappa_{\alpha}\cos\theta }[/math]为测地线曲率[math]\displaystyle{ \kappa_g }[/math]。
于是,我们就将曲线[math]\displaystyle{ \alpha }[/math]的加速度分解为了两部分,它可以写为:
[math]\displaystyle{ \alpha''_{tan}=\kappa_g U\times T }[/math]
以及:
[math]\displaystyle{ \alpha''_{normal}=(\alpha''\cdot U)U }[/math]
我们称[math]\displaystyle{ \alpha }[/math]为测地线,当切仅当[math]\displaystyle{ \alpha''_{tan}=\kappa_g U\times T }[/math]为0。
直观上看,由于曲线[math]\displaystyle{ \alpha }[/math]是一条场速度曲线,所以它的速率不发生变化,而只有方向发生变化。这种变化就体现为一种加速度,只有当这种加速度完全是由于它在曲面引起的时候,它才是一条测地线。
假设你是一只在[math]\displaystyle{ \alpha }[/math]上以常速行走的蚂蚁,那么如果你沿着测地线行走,则你刚好贴到了曲面上,并且不会产生额外的加速度。
测地线方程
下面,我们以[math]\displaystyle{ \{x_u,x_v\} }[/math]为基来推导出测地线所需满足的数学方程。
首先,我们知道[math]\displaystyle{ \alpha'=\textbf{x}_u u'+\textbf{x}_v v' }[/math],于是:
[math]\displaystyle{ \alpha''=\textbf{x}_{uu} u'^2=\textbf{x}_{vv}v'u'+\textbf{x}_u u''+\textbf{x}_{vu}u'v'+\textbf{x}_{vv}v'^2+\textbf{x}_v v'' }[/math]
进一步化简,我们可以得到:
[math]\displaystyle{ \alpha''=\textbf{x}_u\left [{u''+\frac{E_u}{2E}u'^2+\frac{E_v}{E}u'v'-\frac{G_v}{2E}v'^2}\right ] + \textbf{x}_v\left [v''-\frac{E_v}{2G}u'^2+\frac{G_u}{G}u'v'+\frac{G_v}{2G}v'^2\right ]+U\left [lu'^2+2mu'v'+nv'^2\right ] }[/math]
故而,测地线方程为:
[math]\displaystyle{ \begin{align} &u''+\frac{E_u}{2E}u'^2+\frac{E_v}{E}u'v'-\frac{G_v}{2E}v'^2=0\\ &v''-\frac{E_v}{2G}u'^2+\frac{G_u}{G}u'v'+\frac{G_v}{2G}v'^2=0 \end{align} }[/math]
其中,
[math]\displaystyle{ E=\textbf{x}_u\cdot \textbf{x}_u, F=\textbf{x}_u\cdot \textbf{x}_v, G=\textbf{x}_v\cdot \textbf{x}_v }[/math]
[math]\displaystyle{ l=S(\textbf{x}_u)\cdot \textbf{x}_u, m=S(\textbf{x}_u)\cdot \textbf{x}_v=S(\textbf{x}_v)\cdot \textbf{x}_u, n=S(\textbf{x}_v)\cdot \textbf{x}_v }[/math]
非欧几里德空间的情况
度规
在数学中,度规(距离)就是一种将某集合中一对元素之间映射为实数的映射。在微分几何中,我们可以在任意一个曲面(流形)的切向量空间中定义度规,该度规将两个向量映射为一个实数。度规实际上可以看作是对向量的内积以及距离等概念的推广。
假设[math]\displaystyle{ \textbf{u},\textbf{v} }[/math]和[math]\displaystyle{ \textbf{w} }[/math]都是向量空间中的向量,那么度规g是一个双线性函数,满足:
- [math]\displaystyle{ g(a\textbf{u}+b\textbf{v},\textbf{w})=ag(\textbf{u},\textbf{w})+bg(\textbf{v},\textbf{w}) }[/math]
- [math]\displaystyle{ g(\textbf{w},a\textbf{u}+b\textbf{v})=ag(\textbf{w},\textbf{u})+bg(\textbf{w},\textbf{v}) }[/math]
这就是所谓的双线性。如果对任意的向量:[math]\displaystyle{ \textbf{u},\textbf{u}, g(\textbf{u},\textbf{u})\gt 0 }[/math]始终成立,我们就称g为正定的。
举例:
[math]\displaystyle{ g(\textbf{u},\textbf{v})=\textbf{u}\cdot \textbf{v} }[/math]
也就是说,向量的内积实际上也是一种度规。
再比如:
设曲面M,它的位于z=0的上半平面上,[math]\displaystyle{ M=\{(x,y)\in R^2 | y\gt 0\} }[/math],假设M上的任意一点可以写成:[math]\displaystyle{ \textbf{x}=(u,v) }[/math]的形式,其中u,v是曲面的坐标。对于该曲面上的任意两个向量[math]\displaystyle{ \textbf{w}_1,\textbf{w}_2 }[/math],我们定义度规g为:
[math]\displaystyle{ g(\textbf{w}_1,\textbf{w}_2)=\frac{\textbf{w}_1\cdot \textbf{w}_2}{v^2} }[/math]
可以验证,这个度规g满足双线性的要求。这一具备该度规的曲面M被称为彭加莱平面。
当给定切向量空间中的一组基以后,我们可以将度规表示为一个矩阵(因为度规是一个双线性映射)。即:
[math]\displaystyle{ g(\textbf{x},\textbf{y})=\textbf{x}^TA\textbf{y} }[/math]
这里[math]\displaystyle{ \textbf{x},\textbf{y} }[/math]都是切向量,并在一组基下相应地展开了,A是度规g对应的矩阵。
这样,比如普通的内积对应的矩阵就是单位阵,而彭加莱平面的矩阵就是:
[math]\displaystyle{ \left( \begin{matrix} \frac{1}{v^2} & 0\\ 0&\frac{1}{v^2}\\ \end{matrix} \right) }[/math]
在度规下的曲率和测地线
我们看到在对于空间曲面的所有讨论中,都仅仅涉及到对切向量的内积。只要我们将内积替换为度规将不会影响各个数学表达式的形式。所以,我们可以得到更一般度规下面的一些重要公式。
比如含有度规的高斯曲率定义为:
[math]\displaystyle{ K=-\frac{1}{2\sqrt{EG}}\left( \frac{\partial}{\partial v}\left(\frac{E_v}{\sqrt{EG}}\right)+\frac{\partial}{\partial u}\left(\frac{G_u}{\sqrt{EG}}\right)\right) }[/math]
其中 [math]\displaystyle{ E=g(\textbf{x}_u, \textbf{x}_u), F=g(\textbf{x}_u, \textbf{x}_v), G=g(\textbf{x}_v, \textbf{x}_v) }[/math]
测地线方程则和没有度规情况下一样。
举例:彭加莱平面
下面,我们以彭加莱平面为例来做一些简单的计算。
首先,我们知道[math]\displaystyle{ \textbf{x}_u=(1,0),\textbf{x}_v=(0,1) }[/math]
这样,我们就可以计算出了
[math]\displaystyle{ E=g(\textbf{x}_u,\textbf{x}_u)=\frac{1}{v^2}, F=g(\textbf{x}_u,\textbf{x}_v)=0, G=g(\textbf{x}_v,\textbf{x}_v)=\frac{1}{v^2} }[/math]
故而,[math]\displaystyle{ G_u=0, E_v=-\frac{2}{v^3} }[/math],所以高斯曲率为:
[math]\displaystyle{ K=-\frac{1}{2\sqrt{1/v^4}}\left( \frac{\partial}{\partial v}\left( \frac{-2/v^3}{\sqrt{1/v^4}}\right)\right)=-1 }[/math]
因此,在彭加莱平面上的每一个点,它的曲率都是一个常数,而且是负数。
测地线方程为:
[math]\displaystyle{ u''-\frac{2}{v}u'v'=0, v''+\frac{1}{v}u'^2-\frac{1}{v}v'^2=0 }[/math]
求解后得到:
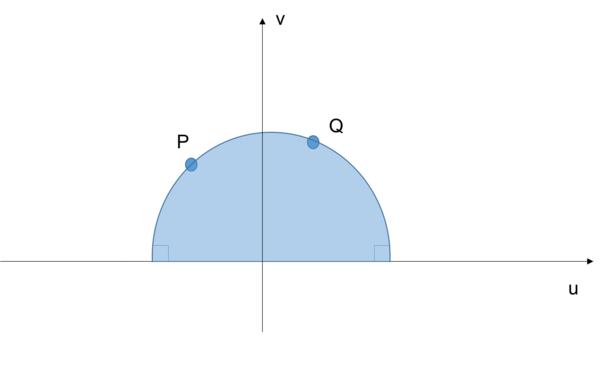
[math]\displaystyle{ (u-d)^2+v^2=1/c^2 }[/math]
这是一个以u上任意点d为圆心,1/c为半径的圆。这就是彭家莱平面上的测地线,如下图所示:
参考文献
- John Oprea: Differential Geometry and Its Applications,Pearson Education, 2004