环
在图论 graph theory中,一个图中的环( Cycle)是一个非空轨迹,其中唯一重复的点是起点和终点。一个有向图中的有向环 Directed cycle同样是非空有向迹线,其中唯一重复的点也是起点和终点。
没有环的图称为无环图 acyclic graph。一个有向图,但是没有有向环,称为有向无环图 Directed acyclic graph。没有环的连接图称为 树 Tree。
定义
回路,环
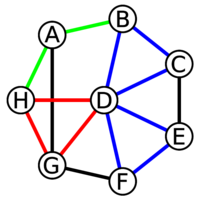
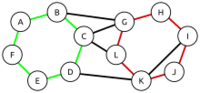
- 回路 Circuit如图所示,以一个具有顶点序列的非空轨迹环为例,其中第一个和最后一个顶点重合。设图[math]\displaystyle{ G =(V,E,ϕ) }[/math],那么回路是具有顶点序列[math]\displaystyle{ (v1,v2,...,vn,v1) }[/math]的非空路径[math]\displaystyle{ (e1,e2,…,en) }[/math]。[1]
- 在一个环或简单回路中,唯一重复的顶点是起点和终点。[1]
- 一个回路(或环)的长度指的是相关连边的数量。
有向回路,环
- 有向回路是一个非空有向路径,其中第一个和最后一个顶点重合出现。设有向图[math]\displaystyle{ G =(V,E,ϕ) }[/math],其有向回路是具有顶点序列[math]\displaystyle{ (v1,v2,...,vn,v1) }[/math]的非空有向路径[math]\displaystyle{ (e1,e2,……,en) }[/math]。[1]
- 在一个有向环或简单有向回路中,唯一重合的顶点是起点和终点。[1]
无弦环
一个图中的 无弦环 Chordless cycles(也可以称为 孔 Hole或 诱导环 Induced cycle),指的是该环中没有两个顶点通过不属于该环的边相连。其反孔部分为此图孔的补图。无弦环i可用于表征 完美图 perfect graphs:通过强完美图定理 strong perfect graph theorem,当且仅当它的孔或反孔部分中无奇数(且大于3)个顶点时,图才是完美的。弦图是完美图的特殊形式,即没有任何长度大于三的孔。
图的 围长 girth是其最小环的长度;并且这个环必须是无弦的。 笼 cages定义为具有给定度和围长组合的最小正则图。
一个图中的 边环 Peripheral cycle具有以下性质:不在此边环上的两条连边可以通过一条特殊路径连接;该路径内部顶点均不在此边环上。如果一个图中的某条环不是通过添加一条边形成的,那么其边环肯定是诱导环。
环空间
“环“还可以指代一个图中环空间 Cycle space内的一个元素。在一个图中存在很多环空间,且每个都有对应的系数域 Coefficient field或 环 Ring(代数)。最常见的是 二元环空间 Binary cycle space(通常简称为环空间),它是由在该图中每个顶点上具有偶数度的边集组成。二元环空间在二元域上形成了一个向量空间 Vector space。根据 维布伦定理 Veblen's theorem,该环空间的每个元素都可以形成为简单环的不相交边的并集。该图的 环基 Cycle basis相当于一组简单环,它们构成了环空间的基。[2]
根据 代数拓扑 Algebraic topology的思想, 二元环空间 Binary cycle space可以推广为其它 环 Ring中的 向量空间 Vector spaces或 模 Module,例如整数,有理数或实数等。[3]
环检测
关于环在有向或无向图中的存在,可以通过深度优先搜索 depth-first search(DFS)来确定。具体方法是查找是否存在一条连边指向当前顶点的原始点(包括回边)。[4]DFS跳过的所有回边都是环的一部分。[5]在无向图中,指向一个节点上级的连边不应算作后边,但是如果找到任何其他已访问的顶点可以视为后边。在无向图的情况下,只需要[math]\displaystyle{ \mathcal{O}(n) }[/math]时间即可在[math]\displaystyle{ n }[/math]个顶点图中找到一个循环,因为最多[math]\displaystyle{ n-1 }[/math]个边可以是树边。
很多拓扑排序 Topological sorting算法也可以用于检测环,因为这些环阻碍了拓扑排序。另外,因为环本身性质是强连接的,所以如果一个有向图被划分为具有强连接的不同组成部分,则环仅存在于这些组成部分内,也并非它们之间。[5]
对于有向图的环检测,可以使用基于分布式消息的算法。其概念是环中的某一个顶点发出了一条消息并最终返回,因此被称为 分布式环检测算法 Distributed cycle detection algorithms。通过在计算机集群(或超级计算机)上使用分布式图形处理系统,该方法非常适合大规模图的运算。
环检测的应用还包括使用 等待图 Wait-for graphs来检测并发系统中的 死锁 Deadlocks。
[6]
环覆盖图
莱昂哈德·欧拉 Leonhard Euler在1736年发表的关于柯尼斯堡七桥 Seven Bridges of Königsberg的论文后来被广泛认为是图论的起源。论文中,Euler做出了以下证明:对于一个具有封闭行走路线的有限无向图,要求访问者恰好经过每条边一次。其充要条件是除了孤立的顶点(即,所有边都被两两顶点相连)之外,其他每个顶点都是偶数度。一旦该有向图满足能一次性访问所有边不重复的特征,那么它就具有强连接性,并且每个顶点的进入次数和离开次数必定相等。无论哪种情况,其访问轨迹均被称为欧拉环或欧拉环游。如果一个有限的无向图在其每个顶点上都具有偶数度,那么不管其是否相连,均有可能找到一组简单的环,使满足恰好覆盖该图的每个边一次:这即是 维勃伦定理 Veblen's theorem。[7] 当一个连通图不满足欧拉定理的条件时,通过解决邮路问题 Route inspection problem,可以在多项式时间中找到覆盖每个边的最短闭合路径。
相较之下,寻找覆盖每个顶点仅一次而不是覆盖连边的简单环问题要困难得多。这种环被称为哈密顿环 Hamiltonian cycle,确定其存在性的过程属于NP-完全问题。[8]
目前诸多包含哈密顿环的相关图类研究被发表。其中一个例子是奥尔定理 Ore's theorem,如果一个图中每个不相邻的顶点对的度数之和最少等于该图中顶点总数,那么该图中必然有哈密顿环。[9]
双圈覆盖猜想 Cycle double cover conjecture指出,对于每个无桥图,都存在一组简单环可以将图的每个边缘恰好覆盖两次。然而目前其是否成立(或找到反例)仍然是一个悬而未决的问题。[10]
根据环定义的图类
图的几个重要类别可以由其环定义或表征。其中包括:
- 二分图 Bipartite graph,其中无奇数环(具有奇数个顶点的环)。
- 仙人掌图 Cactus graph,其中每个非平凡的双向连通分量都是一个环。
- 环图 Cycle graph,由一个环组成的图。
- 弦图 Chordal graph,其中每个导出环都是三角形。
- 有向无环图 Directed acyclic graph,无环的有向图。
- 线完美图 Line perfect graph,其中每个奇环都是三角形。
- 完美图 Perfect graph,无导出环或大于3的奇数路径长度的环。
- 伪森林 Pseudoforest,其中每个连通分量最多只有一个环。
- 绞窄图 Strangulated graph,其中每个边环都是三角形。
- 强连通图 Strongly connected graph,一种有向图,其中每个边都是环的一部分。
- 无三角形图 Triangle-free graph,无三个顶点环的图。
其他参考资料
- 环空间 Cycle space https://en.wikipedia.org/wiki/Cycle_space
- 环基 Cycle basis https://en.wikipedia.org/wiki/Cycle_basis
- 环检测 Cycle detection 通过迭代函数值序列进行环检测:https://en.wikipedia.org/wiki/Cycle_detection
参考文献
- ↑ 1.0 1.1 1.2 1.3 Bender, Edward A.; Williamson, S. Gill (2010). Lists, Decisions and Graphs. With an Introduction to Probability.
- ↑ Gross, Jonathan L.; Yellen, Jay (2005), "4.6 Graphs and Vector Spaces", Graph Theory and Its Applications (2nd ed.), CRC Press, pp. 197–207, ISBN 9781584885054.
- ↑ Diestel, Reinhard (2012), "1.9 Some linear algebra", Graph Theory, Graduate Texts in Mathematics, vol. 173, Springer, pp. 23–28.
- ↑ Tucker, Alan (2006). "Chapter 2: Covering Circuits and Graph Colorings". Applied Combinatorics (5th ed.). Hoboken: John Wiley & sons. p. 49.
- ↑ 5.0 5.1 Sedgewick, Robert (1983), "Graph algorithms", Algorithms, Addison–Wesley
- ↑ Silberschatz, Abraham; Peter Galvin; Greg Gagne (2003). Operating System Concepts. John Wiley & Sons, INC.. pp. 260. https://archive.org/details/operatingsystemc0006silb.
- ↑ Veblen, Oswald (1912), "An Application of Modular Equations in Analysis Situs", Annals of Mathematics, Second Series, 14 (1): 86–94, doi:10.2307/1967604, JSTOR 1967604.
- ↑ Richard M. Karp (1972), "Reducibility Among Combinatorial Problems" (PDF), in R. E. Miller and J. W. Thatcher (ed.), Complexity of Computer Computations, New York: Plenum, pp. 85–103.
- ↑ Ore, Ø. (1960), "Note on Hamilton circuits", American Mathematical Monthly, 67 (1): 55, doi:10.2307/2308928, JSTOR 2308928.
- ↑ Jaeger, F. (1985), "A survey of the cycle double cover conjecture", Annals of Discrete Mathematics 27 – Cycles in Graphs, North-Holland Mathematics Studies, vol. 27, pp. 1–12, doi:10.1016/S0304-0208(08)72993-1.
编者推荐
巴拉巴西网络科学(课程)
本课程中,有幸邀请了汪小帆、赵海兴、许小可、史定华、陈清华、张江、狄增如、陈关荣、樊瑛、刘宗华这十个来自六大不同高校、在网络科学领域耕耘许久的教授作为导师,依据教材框架,各有侧重地为我们共同勾勒出整个学科的美丽图景,展示这个学科的迷人魅力,指引这个学科的灿烂未来。
知识图谱概述
知识图谱是人工智能的一大技术驱动力,它能够广泛地应用于不同的任务。相比深度学习,知识图谱中的知识可以沉淀,可解释性非常强,类似于人类的思考。近年来,不管是学术界还是工业界都纷纷构建自家的知识图谱,有面向全领域的知识图谱,也有面向垂直领域的知识图谱。其实早在文艺复兴时期,培根就提出了“知识就是力量”,在当今人工智能时代,各大科技公司更是纷纷提出:知识图谱就是人工智能的基础。
本中文词条由Jie翻译,CecileLi审校,思无涯咿呀咿呀编辑,欢迎在讨论页面留言。
本词条内容翻译自 wikipedia.org,遵守 CC3.0协议。