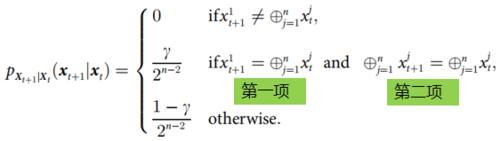基于信息分解的因果涌现理论

简介

基于信息分解的因果涌现理论（框架）

相关概念

信息熵与互信息

在信息论中，熵（英语：entropy，又称信息熵、信源熵、平均自信息量）是接收的每条消息中包含的信息的平均量。这里的“消息”代表来自分布或数据流中的事件、样本或特征。（熵最好理解为不确定性的量度而不是确定性的量度，因为越随机的信源的熵越大。）

在信息论中，随机变量的“熵”量化了与变量的潜在状态或可能结果相关的不确定性或信息的平均水平。考虑到所有潜在状态的概率分布，这衡量了描述变量状态所需的预期信息量。给定一个离散随机变量 [math]\displaystyle{ X }[/math]，其取值于集合 [math]\displaystyle{ \mathcal{X\gt }[/math]，且服从 [math]\displaystyle{ p\colon \mathcal{X}\to[0, 1] }[/math] 分布，则熵为 [math]\displaystyle{ \Eta(X) := -\sum_{x \in \mathcal{X}} p(x) \log p(x), }[/math] 其中 [math]\displaystyle{ \Sigma }[/math] 表示变量可能值的总和。 [math]\displaystyle{ \log }[/math] 的底数（即 对数）的选择因应用不同而不同。

在概率论和信息论中，两个随机变量的互信息（mutual Information，MI）度量了两个变量之间相互依赖的程度。具体来说，对于两个随机变量，MI是一个随机变量由于已知另一个随机变量而减少的“信息量”（单位通常为比特）。互信息的概念与随机变量的熵紧密相关，熵是信息论中的基本概念，它量化的是随机变量中所包含的“信息量”。

离散随机变量 X 和 Y 的互信息可以计算为：

[math]\displaystyle{ \operatorname{I}(X; Y) = \sum_{y \in \mathcal Y} \sum_{x \in \mathcal X} { P_{(X,Y)}(x, y) \log\left(\frac{P_{(X,Y)}(x, y)}{P_X(x)\,P_Y(y)}\right) }, }[/math]

({{{3}}})

其中 [math]\displaystyle{ P_{(X,Y)\gt }[/math] 是 [math]\displaystyle{ X }[/math] 和 [math]\displaystyle{ Y }[/math] 的 联合概率 mass 函数，并且[math]\displaystyle{ P_X }[/math] 和 [math]\displaystyle{ P_Y }[/math] 分别是 [math]\displaystyle{ X }[/math] 和 [math]\displaystyle{ Y }[/math] 的 边际概率 质量函数。

部分信息分解

部分信息分解是信息论的一个扩展，旨在将信息论描述的成对关系推广到多个变量的相互作用。

信息论可以通过 相互信息 [math]\displaystyle{ I(X_1;Y) }[/math] 量化单个源变量 [math]\displaystyle{ X_1 }[/math] 对目标变量 [math]\displaystyle{ Y }[/math] 的信息量。如果我们现在考虑第二个源变量 [math]\displaystyle{ X_2 }[/math]，经典信息论只能描述联合变量 [math]\displaystyle{ \{X_1,X_2\; }[/math] 与 [math]\displaystyle{ Y }[/math] 的相互信息，由 [math]\displaystyle{ I(X_1,X_2;Y) }[/math] 给出。但一般来说，了解各个变量 [math]\displaystyle{ X_1 }[/math] 和 [math]\displaystyle{ X_2 }[/math] 及其相互作用与 [math]\displaystyle{ Y }[/math] 究竟有何关系将会很有趣。

假设我们有两个源变量 [math]\displaystyle{ X_1, X_2 \in \{0,1\; }[/math] 和一个目标变量 [math]\displaystyle{ Y=XOR(X_1,X_2) }[/math]。在这种情况下，总互信息 [math]\displaystyle{ I(X_1,X_2;Y)=1 }[/math]，而个体互信息 [math]\displaystyle{ I(X_1;Y)=I(X_2;Y)=0 }[/math]。也就是说，[math]\displaystyle{ X_1,X_2 }[/math] 关于 [math]\displaystyle{ Y }[/math] 的相互作用产生了 协同 信息，而这无法用经典信息论量轻易捕捉到。

部分信息分解进一步将源变量 [math]\displaystyle{ \{X_1,X_2\; }[/math] 与目标变量 [math]\displaystyle{ Y }[/math] 之间的互信息分解为

[math]\displaystyle{ I(X_1,X_2;Y)=\text{Unq}(X_1;Y \setminus X_2) + \text{Unq}(X_2;Y \setminus X_1) + \text{Syn}(X_1,X_2;Y) + \text{Red}(X_1,X_2;Y) }[/math]

此处各个信息原子定义为

• [math]\displaystyle{ \text{Unq}(X_1;Y \setminus X_2) }[/math] 是 [math]\displaystyle{ X_1 }[/math] 具有的关于 [math]\displaystyle{ Y }[/math] 的“独特”信息，而 [math]\displaystyle{ X_2 }[/math] 中没有这些信息
• [math]\displaystyle{ \text{Syn}(X_1,X_2;Y) }[/math] 是 [math]\displaystyle{ X_1 }[/math] 和 [math]\displaystyle{ X_2 }[/math] 相互作用中关于 [math]\displaystyle{ Y }[/math] 的“协同”信息
• [math]\displaystyle{ \text{Red}(X_1,X_2;Y) }[/math] 是 [math]\displaystyle{ X_1 }[/math] 或 [math]\displaystyle{ X_2 }[/math] 中关于 [math]\displaystyle{ Y }[/math] 的“冗余”信息

整合信息分解

对部分信息分解框架在在方向上的推广。

基本概念

因果涌现框架

马尔科夫系统，信息原子，因果涌现（向下因果，因果解耦）

Rosas的因果涌现理论

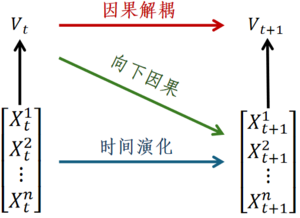
Rosas等从信息分解理论的视角出发，提出一种基于整合信息分解定义因果涌现的方法，并将因果涌现进一步区分为：因果解耦（Causal Decoupling）和向下因果（Downward Causation）两部分。其中因果解耦表示当前时刻宏观态对下一时刻宏观态的因果效应，向下因果表示上一时刻宏观态对下一时刻微观态的因果效应。因果解耦和向下因果的示意图如下图所示，其中微观状态输入为[math]\displaystyle{ X_t\ (X_t^1,X_t^2,…,X_t^n ) }[/math]，宏观状态是[math]\displaystyle{ V_t }[/math]，它由微观态变量[math]\displaystyle{ X_t }[/math]粗粒化而来，因而是[math]\displaystyle{ X_t }[/math]的随附特征（Supervenience），[math]\displaystyle{ X_{t+1} }[/math]和[math]\displaystyle{ V_{t+1} }[/math]分别表示下一时刻的微观和宏观状态。

部分信息分解

该方法建立在Williams和Beer等提出的多元信息非负分解理论的基础之上，该文使用部分信息分解（PID）将微观态和宏观态的互信息进行分解。

不失一般性，假设我们的微观态为[math]\displaystyle{ X(X^1,X^2) }[/math]，即它是一个二维的变量，宏观态为[math]\displaystyle{ V }[/math]，则二者之间的互信息可以被分解为四个部分：

[math]\displaystyle{ I(X^1,X^2;V)=Red(X^1,X^2;V)+Un(X^1;V│X^2 )+Un(X^2;V│X^1 )+Syn(X^1,X^2;V) }[/math]

其中[math]\displaystyle{ Red(X^1,X^2;V) }[/math]表示冗余信息，是指两个微观态[math]\displaystyle{ X^1 }[/math]和[math]\displaystyle{ X^2 }[/math]重复地给宏观态[math]\displaystyle{ V }[/math]提供的信息；[math]\displaystyle{ Un(X^1;V│X^2 ) }[/math]和[math]\displaystyle{ Un(X^2;V│X^1 ) }[/math]表示特有信息，是指每一个微观态变量单独给宏观态提供的信息；[math]\displaystyle{ Syn(X^1,X^2;V) }[/math]表示协同信息，是指所有微观态[math]\displaystyle{ X }[/math]联合在一起给宏观态[math]\displaystyle{ V }[/math]提供的信息。

因果涌现定义

然而，PID框架只能分解关于多个源变量和一个目标变量之间的互信息，Rosas扩展了该框架，提出整合信息分解方法[math]\displaystyle{ \Phi ID }[/math]来处理多个源变量和多个目标变量之间的互信息，还可以用来分解不同时刻间的互信息，作者基于分解后的信息提出了两种因果涌现的定义方法：

1）当特有信息[math]\displaystyle{ Un(V_t;X_{t+1}| X_t^1,\ldots,X_t^n\ )\gt 0 }[/math]，表示当前时刻的宏观态[math]\displaystyle{ V_t }[/math]能超过当前时刻的微观态[math]\displaystyle{ X_t }[/math]给下一时刻的整体系统[math]\displaystyle{ X_{t+1} }[/math]提供更多信息，这时候系统存在着因果涌现；

2）第二种方法绕开了选择特定的宏观态[math]\displaystyle{ V_t }[/math]，仅仅基于系统当前时刻的微观态[math]\displaystyle{ X_t }[/math]和下一时刻的微观态[math]\displaystyle{ X_{t+1} }[/math]之间的协同信息定义因果涌现，当协同信息[math]\displaystyle{ Syn(X_t^1,…,X_t^n;X_{t+1}^1,…,X_{t+1}^n )\gt 0 }[/math]，系统发生了因果涌现。

值得注意的是，对于方法一判断因果涌现的发生需要依赖宏观态[math]\displaystyle{ V_t }[/math]的选择，其中方法一是方法二的下界。这是因为，[math]\displaystyle{ Syn(X_t;X_{t+1}\ ) ≥ Un(V_t;X_{t+1}| X_t\ ) }[/math]衡成立。所以，如果[math]\displaystyle{ Un(V_t;X_{t+1}| X_t\ ) }[/math]大于0，则系统出现因果涌现。然而[math]\displaystyle{ V_t }[/math]的选择往往需要预先定义粗粒化函数，因此无法回避Erik Hoel因果涌现理论的局限。另外一种自然的想法就是使用第二种方法借助协同信息来判断因果涌现的发生，但是协同信息的计算是非常困难的，存在着组合爆炸问题。因此，第二种方法基于协同信息的计算往往也是不可行的。总之，这两种因果涌现的定量刻画方法都存在一些弱点，因此，有待提出更加合理的量化方法。

具体实例

文中作者列举了一个具体的例子(如上式），来说明什么时候发生因果解耦、向下因果以及因果涌现。该例子是一个特殊的马尔科夫过程，这里，[math]\displaystyle{ p_{X_{t+1}|X_t}(x_{t+1}|x_t) }[/math]表示动力学关系，[math]\displaystyle{ X_t=(x_t^1,…,x_t^n )\in \left\{0,1\right\}^n }[/math]为微观态。该过程的定义是通过检查前后两个时刻的变量[math]x_t[/math]和[math]x_{t+1}[/math]的取值，也就是判断[math]x_t[/math]的所有维度模2求和是否与[math]x_{t+1}[/math]的第一个维度相同来确定下一时刻状态[math]x_{t+1}[/math]取不同数值概率的：如果不同，则概率取0；否则则再判断[math]x_t,x_{t+1}[/math]在所有维度上是否都有相同的模2和，如果两个条件都满足，则取值概率为[math]\gamma/2^{n-2}[/math]，否则取值概率为[math](1-\gamma)/2^{n-2}[/math]。这里[math]\gamma[/math]为一个参数，[math]n[/math]为x的总维度。

实际上，如果[math]\displaystyle{ \sum_{j=1}^n x^j_t }[/math]是偶数或者0时[math]\displaystyle{ \oplus^n_{j=1} x^j_t:=1 }[/math]，反之[math]\displaystyle{ \oplus^n_{j=1} x^j_t:=0 }[/math]，因此[math]\displaystyle{ \oplus^n_{j=1} x^j_t }[/math]的结果是X整体序列的奇偶性，而第一个维度则可以看作是一个奇偶校验位。[math]\displaystyle{ \gamma }[/math]实际上表示X序列某两个位产生了突变，并且该突变却能够保证整体序列的奇偶性不变，以及序列的奇偶校验位也符合序列整体的实际奇偶性的概率。

因而该过程的宏观态可以就看做是整个序列所有维度和的奇偶性，该奇偶性的概率分布是微观态的异或计算的结果。[math]x_t^1[/math]是一个特殊的微观态，它始终与上一时刻序列的宏观态保持一致。因此，当第二个判断条件中只有第一项成立时该系统发生向下因果条件，只有第二项成立时系统发生因果解耦，两项同时成立时则称系统发生因果涌现。

因果涌现充分指标

受计算的局限而提出的用于识别因果涌现的充分条件（三个指标）。

应用案例

文中的三个案例（生命游戏，鸟群，猴脑）

与同类框架的比较

与EI，可逆性因果涌现原理，矩阵论因果涌现等框架的比较。