基于有效信息的因果涌现理论

基于有效信息的因果涌现理论是该领域最早提出的一种用于定量刻画因果涌现强度的方法。该方法由Erik Hoel等人提出，其基本思想是将微观系统进行粗粒化后，使用一种因果效应度量指标有效信息来量化一个马尔科夫动力学的因果性强弱改变。如果粗粒化后的宏观系统的有效信息大于微观系统，那么就认为发生了因果涌现。

起源

2013年，Erik Hoel首次使用“有效信息”指标定量刻画涌现，并提出了因果涌现理论。

2016年，针对多时空尺度的系统提出新的Umax因果效能度量指标

2017年，因果容量与信息通道：将有效信息与信息论中经典概念香农的信道容量进行类比。

2021年，提出因果几何框架，将有效信息概念从离散马尔可夫动力系统拓展至连续系统，

主要理论

马尔科夫动力系统

最初，基于有效信息的因果涌现理论是基于离散状态的马尔科夫动力学，即马尔科夫链展开定量化描述的。

马尔科夫链是指一种状态离散、时间离散的平稳随机过程，描述的是一组随机变量[math]X_t[/math]在状态空间[math]\mathcal{X}=\{1,2,\cdots,N\}[/math]上的取值，其中[math]t[/math]通常表示时间。其动力学一般可以用转移概率矩阵描述(Transitional Probability Matrix)，简称TPM。该矩阵是一个概率矩阵，其中第[math]i[/math]行，第[math]j[/math]列元素[math]p_{ij}[/math]，表示任意时刻[math]t[/math]，系统在[math]i[/math]状态的条件下，下一时刻转移到[math]j[/math]状态的概率。因此，转移概率矩阵每一行均满足归一化条件：

[math]\displaystyle{ \sum_{j=1}^Np_{ij}=1, }[/math]

任意时刻[math]t+1[/math]上的状态概率分布，即[math]Pr(X_{t+1})[/math]，可以被上一时刻的状态概率分布[math]Pr(X_t)[/math]和状态转移矩阵唯一确定，即满足：

[math]\displaystyle{ Pr(X_{t+1}=j)=\sum_{i=1}^N p_{ij}\cdot Pr(X_t=i), }[/math]

这里的[math]i,j\in \mathcal{X}[/math]，是[math]\mathcal{X}[/math]中的任意状态，且[math]N=\#(\mathcal{X})[/math]，即[math]\mathcal{X}[/math]中的总状态数。

粗粒化映射

微观元素状态集[math]S_m[/math]通过[math]M: S_m \rightarrow S_M[/math]映射构成宏观元素状态集[math]S_M[/math]，映射方法可以针对微观元素的空间或（和）时间维度。空间映射的对象是不同微观元素状态，时间映射针对的是同一微观元素不同时间步的状态。

例如，两个微观布尔元素有四种状态[math]S_m = \{00,01,10,11\}[/math]，按照[math]M:[[00,01,10] = off, [11] = on][/math]的映射规则，可以得到宏观尺度一个元素的两种状态，即[math]S_M = \{on, off\}[/math]。

具体要求：粗粒化映射对微观元素而言，必须是穷尽(exhaustive)和互斥的(disjunctive)，即一个微观元素的所有状态必须映射到同一个宏观元素的各种状态。粗粒化映射会带来系统的状态空间减小，但也允许宏观元素可以由单个微观元素组成。

量化方法

下面将引入有效信息这一关键指标，介绍如何基于该指标量化马尔科夫动力系统的因果效应。

有效信息

有效信息（Effective Information，简称EI）是因果涌现理论中的一个核心概念，它可以用来度量一个马尔科夫动力学的因果效应强度。

• EI定义

首先，我们先定义一般情况下的有效信息。因果效应度量的是系统动力学机制的有效性，即在给定动力学的情况下，因、果变量状态分布之间的关联程度（其中不能有混淆变量干扰）。由此可见，EI核心目标并非衡量是否存在因果效应，而是关注效应的强度，且更适用于已经明确存在因果关联的场合。更正式地，EI是因果机制的函数，而与其它因素无关，定义如下：

[math]\displaystyle{ EI(P)\equiv I(Y;X|do(X\sim U)) }[/math]

这里，[math]X[/math]是因变量，[math]Y[/math]是果变量，[math]P[/math]表示[math]X[/math]到[math]Y[/math]的因果机制。当[math]X, Y[/math]均为离散状态分布的情境下，[math]P[/math]为概率转移矩阵，[math]p_{ij}\equiv Pr(Y=j|X=i)[/math]。[math]do(X\sim U(\mathcal{X}))[/math]代表对[math]X[/math]实施do干预(或称do操作，英文是do-operator），使其服从[math]\mathcal{X}[/math]上的均匀分布[math]U(\mathcal{X})[/math]，也即是最大熵分布。在这一干预下，因果机制P保持不变。EI指标度量的是经过do干预后的因变量X与果变量Y之间的互信息。

do干预这一步是根据Judea Pearl的因果阶梯理论提出的。该理论中，因果推断包含了三个层次，分别是：关联、干预和反事实。阶梯层级越高，因果特征越明显。在EI的定义中引入了[math]do[/math]操作上升到干预层级，即设定变量为某个值或服从某个分布，使得EI能够比直接计算互信息更能体现因果特征。从实际意义上来讲，在EI的计算中引入do操作，可以把数据和动力学分开，消除数据分布（即[math]X[/math]的分布）对EI度量所带来的影响，均匀分布也避免了对数据的“偏见”。从因果图角度来看，do操作可以消除EI中的所有指向因变量[math]X[/math]的因果箭头，包括其它变量（包括不可观测的变量）对[math]X[/math]的影响，从而使得EI更能够刻画动力学本身的特性。

• 马尔科夫动力系统EI

回到离散状态的马尔科夫链中，任意时刻的状态变量[math]X_t[/math]可以看作是原因，而下一时刻的状态变量[math]X_{t+1}[/math]就可以看作是结果，马尔科夫链的状态转移矩阵就是它的因果机制。因此，马尔科夫链的有效信息定义如下：

[math]\displaystyle{ \begin{aligned} EI &= I(X_t,X_{t+1}|do(X_t\sim U(\mathcal{X})))=I(\tilde{X}_t,\tilde{X}_{t+1}) \\ &= \sum^N_{i=1}\sum^N_{j=1}Pr(\tilde{X}_t=i,\tilde{X}_{t+1}=j)\log \frac{Pr(\tilde{X}_t=i,\tilde{X}_{t+1}=j)}{Pr(\tilde{X}_t=i)Pr(\tilde{X}_{t+1}=j)}\\ &= \sum^N_{i=1}Pr(\tilde{X}_t=i)\sum^N_{j=1}Pr(\tilde{X}_{t+1}=j|\tilde{X}_t=i)\log \frac{Pr(\tilde{X}_{t+1}=j|\tilde{X}_t=i)}{Pr(\tilde{X}_{t+1}=j)}\\ &= \frac{1}{N}\sum^N_{i=1}\sum^N_{j=1}p_{ij}\log\frac{N\cdot p_{ij}}{\sum_{k=1}^N p_{kj}} \end{aligned} }[/math]

同理，[math]\displaystyle{ \tilde{X}_t,\tilde{X}_{t+1} }[/math]分别为把[math]X_t[/math]干预为均匀分布后，[math]t[/math]时刻与下一时刻的状态。[math]\displaystyle{ p_{ij} }[/math]为第i个状态转移到第j个状态的转移概率，[math]N[/math]为总状态数。从这个式子，不难看出，EI仅仅是概率转移矩阵[math]P[/math]的函数。

进一步，为方便计算，我们也可以将转移概率矩阵[math]P[/math]写成[math]N[/math]个行向量拼接而成的形式，即：

[math]\displaystyle{ P=(P_1^T,P_2^T,\cdots,P_N^T)^T }[/math]

其中，[math]P_i[/math]矩阵[math]P[/math]的第[math]i[/math]个行向量，且满足条件概率的归一化条件：[math]||P_i||_1=1[/math]，这里的[math]||\cdot||_1[/math]表示向量的1范数。那么EI可以写成如下的形式：

[math]\displaystyle{ \begin{aligned} EI &= \frac{1}{N}\sum^N_{i=1}\sum^N_{j=1}p_{ij}\log\frac{N\cdot p_{ij}}{\sum_{k=1}^N p_{kj}}\\ &=\frac{1}{N}\cdot \sum_{i=1}^N\left(P_i\cdot \log P_i - P_i\cdot\log \bar{P}\right)\\ &=\frac{1}{N}\sum_{i=1}^N D_{KL}(P_i||\bar{P}) \end{aligned} }[/math] 将矩阵每列求均值，可得到平均转移向量[math]\displaystyle{ \overline{P}=\sum_{k=1}^N P_k/N }[/math]。[math]D_{KL}[/math]便是两个分布的KL散度。因此，EI是转移矩阵每个行转移向量[math]P_i[/math]与平均转移向量[math]\bar{P}[/math]的KL散度的均值。 计算实例 下面，给出三个马尔科夫链的例子，以及相应的EI数值也放到了下面： {

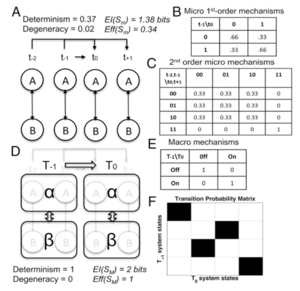
(+马尔科夫链示例)

[/math]和[math]β = {B_t, B_{t+1}}[/math](图D)。

宏观尺度：在宏观时间尺度下的 [math]EI(S_M) = 2 \text{ bits}[/math]，[math]Eff(S_M) = 1[/math], [math]CE(S) = 0.62 \text{ bits}[/math]，系统变得完全确定性和非简并 (图E, F)。

时空因果涌现

因果涌现还可以在空间、时间上同步发生，下面对图中实例进行具体分析：

系统机制：

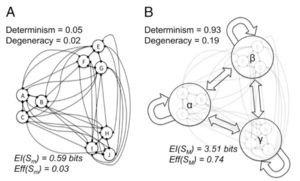
• 元素机制：所有微观元素也遵循二阶马尔可夫机制，整合两个微时间步([math]t_{-2}[/math], [math]t_{-1}[/math]和[math]t_0[/math], [math]t_{+1}[/math])的输入，作出响应。所有微观元素自发活动（发放状态：0，1），具有非均匀的发放概率:[math]p(A/D/G) = 0.45[/math];[math]p(B/E/H) = 0.5[/math];[math]p(C/F/I) = 0.55[/math]。
• 组机制：所有元素被划分为三组[math]{ABC, DEF, GHI}[/math]，在每组内，如果两个时间步内组内连接之和[math]\sum(intra) = 0[/math]，接下来的两个时间步所有元素保持为0。然而，如果在两个时间步中，与另外两组中的组间连接之和[math]\sum(inter) = 6[/math]，则在接下来的两个时间步中，发放概率提高0.5。

微观尺度：微观尺度下的系统具有 [[math]EI(S_m) = 0.59 \text{ bits}[/math]; [math]Eff(S_m) = 0.033[/math]]

粗粒化映射：在宏观尺度[math]S_M[/math]，三组神经元分组为宏观成分，两个微观时间步长([math]t_x[/math])聚合为一个宏观时间步长([math]T_x[/math])(图B)。

宏观尺度：粗粒化后的系统具有更高的[math]EI(S_M) = 3.51 \text{ bits}[/math]，和[math]Eff(S_M) = 0.74[/math]。时空因果涌现发生，[math]CE(S) = 2.92 \text{ bits}[/math]，即粗粒化过后系统确定性的增加，增加程度远超简并性的增加与状态集的减小。

注：本例对应于真实神经元中，宏观成分可表示为有三种状态的“微柱”:“抑制态inhibited”(所有微柱神经元均在Tx时静默)，“感受态receptive”(部分在Tx时放电)和“爆发态bursting”(所有均在Tx处放电)。相应地，宏观的因果相互作用可以总结为，如果其中一个宏观成分处于抑制态，那么只有接收到一次发放才能转换到接受态或（不太可能的）爆发态；否则，它将一直保持抑制态。

应用

复杂网络，生物系统

缺陷与争议

1.依赖粗粒化方法 2.实际适用性