元胞自动机

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
费米子（讨论 | 贡献）2020年4月19日 (日) 16:10的版本 （→‎相关链接）
跳到导航 跳到搜索


‘’‘元胞自动机 cellular automata’‘’（CA） ，中文也译作细胞自动机、点格自动机、分子自动机或单元自动机，是一种时间、空间、状态都离散，空间相互作用和时间因果关系为局部的网格动力学模型，具有模拟复杂系统时空演化过程的能力。由冯·诺依曼创始，经数学家约翰·何顿·康威 John Horton Conway、物理学家斯蒂芬·沃尔夫勒姆 Stephen Wolfram等人的贡献后迅速发展。‘’‘元胞自动机’‘’广泛应用于‘’‘计算机科学’‘’、物理学、复杂系统 Complex Systems，理论生物学和微观结构模型等领域。元胞自动机同时也被称为元胞空间，棋盘自动机 tessellation automata，同质结构，元胞结构，棋盘结构和迭代数组。[1]

基于元胞自动机的三维展示


元胞自动机由规则的元胞网格组成，散布在规则格网（Lattice Grid）中的每一元胞（Cell）取有限的离散状态，遵循同样的作用规则，依据确定的局部规则作同步更新。

首先每个单元格都处于有限状态中的一种，例如打开状态和关闭状态（与耦合映象晶格 coupled map lattice相反）。网格可以是任意有限维数。对于每个单元格，都有一组定义为其邻域的单元格。 每个单元格都将被定义一种状态来作为初始状态（时间t = 0）。根据一些固定的规则（通常是一种数学函数）[2]，产生新的状态（t增加1个单位）。单元格当前状态及其附近单元格的状态共同决定了该单元格的新状态。一般而言，更新单元格状态的规则对于每个单元格都是相同的，不随时间变化，适用于整个网格。[3]然而也有例外，例如随机元胞自动机和异步元胞自动机。


20世纪40年代，这个概念最初是由当时在洛斯阿拉莫斯国家实验室 （Los Alamos National Laboratory）工作的斯坦尼斯瓦夫•乌拉姆（Stanislaw Ulam）和约翰·冯·诺依曼 John von Neumann发现的。尽管20世纪50年代到60年代一直有学者在研究这个问题，但直到20世纪70年代，随着康威的生命游戏 Conway's Game of Life的问世（一个二维的元胞自动机），这个问题才引起学术界的关注。20世纪80年代，史蒂芬·沃尔夫勒姆 Stephen 沃尔弗拉姆对一维元胞自动机进行了系统的研究，他称其为初等元胞自动机。他的研究助理马修·库克（Matthew Cook）指出，这些规则是图灵完备 Turing-complete的。沃尔弗拉姆在2002年发表了《一种新科学 a New Kind of Science》这一著作，文中指出元胞自动机已在许多科学领域得到应用，包括计算机处理器和密码学。

概述

红色单元格是蓝色单元格的摩尔邻域
红色单元格是蓝色单元格的冯·诺依曼邻域。扩展的邻域也包括粉色单元格


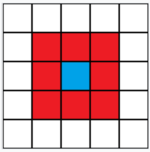
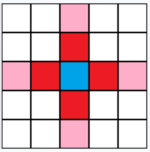
模拟二维元胞自动机的一种方法是用一张无限大的方格纸，加上一套元胞规则来构成。每个正方形被称为“单元格” ，每个单元格有两种可能的状态，黑色和白色。 单元格的邻域是指周围的单元格。 最常见的两种邻域类型有冯诺依曼邻域（von Neumann neighborhood）和摩尔邻域 Moore neighborhood。前者由4个正交相邻的单元格组成。 后者包括冯诺依曼领域和斜对角相邻的4个单元格。[4]对于每个单元格及其摩尔邻域，有512(29)种可能的自动机模式。 对于每一种模式，规则表将确定在下一个时间段中中心单元格是黑色还是白色。康威的生命游戏 Conway's Game of Life就是这种模式的一个流行版本。 另一种常见的邻域类型是扩展的冯诺依曼邻域，它包括每个正交方向上最近的2个单元格，总共8个单元格。[4]这种规则的一般方程是 kks，其中 k 是一个单元格可能状态的数目，s 是用来确定单元格下一个状态的相邻单元格的数目(包括要计算的单元格本身)。[5] 因此，在二维的摩尔邻域中，可能出现的自动机模式共有229个，即1.34*10154个。



通常假设整个网格中除了有限数量的单元格处于不同状态之外，其他的每个单元格具有相同的初始状态。这些状态值的分配被称为配置 configuration。[6]更笼统地说，人们有时假设整个网格从一开始时就具有周期性模式，只有有限数量的单元格违反了这个模式。这种假设在一维元胞自动机中很常见。


元胞自动机通常是在有限网格上模拟的，而不是在无限网格上。在二维空间中，整个网格将是一个矩形而不是一个无限平面。有限网格最大的问题就是如何处理边缘的单元格。处理它们的方式将影响网格中所有单元格的值，一种方法是允许这些单元格中的值保持不变；另一种方法是为这些单元格定义不同的邻域。


虽然可以认为边缘单元格的邻域较少，但是必须为其定义新规则。这些单元格通常以环形排列处理: 当一个单元格无上邻域时，将该单元格相应位置的网格底部单元格作为上邻域，当一个单元格无左邻域时，将该单元格相应位置的网格右侧单元格作为右邻域（这实质上模拟了无限周期的拼接，在偏微分方程领域有时被称为周期边界条件)。这可以想象为用胶带把矩形的左右边缘粘在一起形成一个管状，然后把管的顶部和底部边缘粘在一起形成一个圆环(甜甜圈形状)。其他维度的网格也是这样处理的。这种方法不仅解决了邻域的边界问题，而且易于通过使用模块化计算功能编程。例如，在一维元胞自动机中，单元格 xit 的邻居是{ xi-1t-1，xit-1，xi+1t-1} ，其中 t 是时间步长(纵轴)，i 是一代中的索引(横轴)。


圆环:甜甜圈形状

研究历史


20世纪40年代，乌拉姆在洛斯阿拉莫斯国家实验室工作时，以简单的晶格网络为模型，研究了晶体的生长。[7]与此同时，乌拉姆在洛斯阿拉莫斯的同事约翰·冯·诺依曼 John von Neumann正在研究自复制系统的问题。他最初的设计是基于“一个机器制造另一个机器”的概念。这种设计被称为运动学模型。[8][9]冯·诺依曼在开发这一设计时，逐渐意识到制造一个自我复制的机器人非常困难，并且需要花费巨大成本为机器人提供“一大堆零件”来制造复制品。冯·诺依曼在1948年的希克森研讨会 Hixon Symposium上写了一篇题为《The general and logical theory of automata》的论文。[6]乌拉姆建议使用离散系统来创建自我复制的还原论模型。[6][10]尼尔斯·阿尔·巴里切利对这些人工生命模型进行了许多早期的探索。


乌拉姆和冯·诺依曼在20世纪50年代后期创造了一种计算流体运动的方法。该方法的驱动概念是将流体视为一组离散单元格，根据其相邻单元格的行为计算其运动。[10] 因此诞生了第一个元胞自动机系统。 与乌拉姆的晶格网络一样，冯·诺依曼的元胞自动机 Cellular Automata是二维的，其自复制器通过算法实现。这样的设计使得一个通用复制和构造器在具有很小邻域的元胞自动机内工作(只有那些接触的单元格是邻域；对于冯·诺依曼的元胞自动机而言，只有正交的单元格是邻域)，其中，每个单元格有29个状态。[11]冯·诺依曼通过设计一个20万个元胞的结构，证明了在特定的模式下，单元格可以在给定的网格中无止境地自我复制。这种设计被称为棋盘模型，也被称为冯·诺依曼通用构造器。[12]


冯·诺依曼在实验室的身份证照片


同样在20世纪40年代，诺伯特·维纳和阿图罗·罗森布鲁斯开发了一种具有元胞自动机特征的可激发介质模型。[13]它用于心脏系统脉冲传导的数学描述。 然而该模型并不属于元胞自动机，因为信号传播的介质是连续的，波前是曲线。[13][14]1978年，J.m. Greenberg和S. P. Hastings发展并研究出了一个真正的种可激发介质的元胞自动机。维纳和罗森布鲁斯的原始著作中包含了许多见解，在现代关于心律失常和兴奋系统的研究出版物中仍经常被引用。[15]


到20世纪50年代末，人们已经注意到，元胞自动机可视为并行计算机，特别是在20世纪60年代，一系列形式越来越详细和技术性的定理（通常类似于图灵机的定理）被证明具有形式化的计算能力。[11]


20世纪60年代，人们将元胞自动机作为动力系统的一种特殊类型进行了研究，首次建立了其与符号动力学中的数学领域的联系。1969年， Gustav Arnold Hedlund根据这一观点[16]在论文中汇编了许多结果，至今该论文仍被认为是元胞自动机数学研究的开创性论文。最基本的结果是在Curtis-Hedlund-Lyndon 定理中将元胞自动机的全局规则集描述为移位空间的连续自同态集。


1969年，德国计算机先驱康拉德·楚泽 Konrad Zuse出版了《Calculating Space》，提出宇宙的物理定律本质上是离散的，整个宇宙是在一个元胞自动机的确定性计算的输出。 楚泽理论 Zuse theory成为数字物理学研究领域的基础。[6]


也是在1969年，计算机科学家埃尔维·雷·史密斯 Alvy Ray Smith完成了斯坦福大学关于元胞自动机理论的博士论文。许多论文都出自这篇论文: 他展示了各种形状邻域的等价性，如何把摩尔邻域归结为冯诺依曼邻域，或者如何把任何邻域归结为冯诺依曼邻域。[17] 他证明了二维元胞自动机具有计算通用性，通过引入一维元胞自动机，表明即使在简单的邻域内二维元胞自动机同样具有计算通用性，也是如此。[18] 他展示了如何将复杂的冯诺依曼结构普遍性证明(以及由此产生的自复制机器)纳入到一维元胞自动机计算普遍性的结果中。[19] 作为冯·诺依曼关于元胞自动机书的德文版介绍，他撰写了一份该领域的调查报告，其中引用了几十篇参考文献，这些文献是多个国家的多个作者在过去十年左右时间的研究成果，常常被现代元胞自动机研究者所忽视。[20]



在20世纪70年代，一种名为康威的生命游戏 Conway's Game of Life的两态、二维元胞自动机广为人知，尤其是在早期的计算机界。该元胞自动机是约翰·何顿·康威 John Horton Conway发明的，马丁·加德纳 Martin Gardner在《Scientific American》的一篇文章中推广[21] ，其规则如下:

  1. 任何单元格的邻域单元格状态为活的少于两个，那么该单元格的状态就为死，这可能是由于人口不足造成的。
  2. 任何单元格具有两个或三个状态为活的邻域单元格，那么该单元格状态为活。
  3. 任何单元格具有超过三个状态为活的邻域单元格，那么该单元格状态为死，这可能是由于人口过剩造成的
  4. 任何状态为死的单元格的邻域若正好有三个状态为活的单元格，那么在下一时间段中，该单元格状态会变为活，就像繁殖一样。


尽管简单，该系统实现了令人印象深刻的多样性行为，在表观随机性和顺序之间波动。 生命游戏最明显的特征之一就是“滑翔机”的频繁出现，滑翔机的排列实质上是使自己在网格上移动。也可以安排自动机使滑翔机相互作用来执行计算。经过大量的努力，已经证明生命游戏可以模仿通用图灵机。[22] 在20世纪70年代初期，它主要被看做一个娱乐性游戏，除了研究生命游戏的特殊性和一些相关规则外，很少有人进行后续的研究工作。


斯蒂芬·沃尔夫勒姆 Stephen Wolfram在考虑了自然界中如何形成违反热力学第二定律的复杂模式后，于1981年中开始独立从事元胞自动机的研究。[11]他的研究源于对神经网络等建模系统的兴趣。[11]1983年6月，他在《Reviews of Modern Physics》上发表了他的第一篇论文，研究了初等元胞自动机(特别是第30条规则)。[1][11]这些简单规则行为的意想不到的复杂性使得沃尔弗拉姆怀疑自然界的复杂性可能是由于类似的机制造成的。[11]然而，他的研究使他认识到元胞自动机在模拟神经网络方面的效果很差。此外，沃尔弗拉姆还阐述了内在随机性和计算不可约性的概念，[11]并提出第110条规则，这条规则可能是通用的——在20世纪90年代，沃尔弗拉姆的研究助手马修·库克 Matthew Cook证明了这一事实。[23]


2002年，沃尔弗拉姆发表了一篇1280页的文章《一种新科学 a New Kind of Science》 其中详细论述了关于元胞自动机的发现不是孤立的事实，而是相互依靠的，并且对所有科学学科都有重要意义。[11]尽管书中的内容很混乱[24] [25]，但它描述了一些基于元胞自动机的具体物理模型，它也提供了基于性质不同而形成的抽象系统模型。[11] 然而有一个缺点就是：该书并未对基于元胞自动机的物理学基本理论进行论证。

分类

沃尔弗拉姆在《一种新科学 a New Kind of Science》和20世纪80年代中期的几篇论文中，将元胞自动机和其他几种简单的计算模型根据其行为进行分为四个类别: 

(1)平稳型：自任何初始状态开始,经过一定时间运行后，元胞空间趋于一个空间平稳的构形，这里空间平稳即指每一个元胞处于固定状态。不随时间变化而变化。

(2)周期型：经过一定时间运行后，元胞空间趋于一系列简单的固定结构 Stable Paterns 或周期结构 Perlodical Patterns。由于这些结构可看作是一种滤波器 Filter，故可应用到图像处理的研究中。

(3)混沌型：自任何初始状态开始，经过一定时间运行后，元胞自动机表现出混沌的非周期行为，所生成的结构的统计特征不再变化，通常表现为分形分维特征。

(4)复杂型：出现复杂的局部结构，或者说是局部的混沌，其中有些会不断地传播。从另一角度，元胞自动机可视为动力系统，因而可将初试点、轨道、不动点、周期轨和终极轨等一系列概念用到元胞自动机的研究中。

从另一角度，元胞自动机可视为动力系统，因而可将初始点、轨道、不动点、周期轨和终极轨等一系列概念用到元胞自动机的研究中，上述分类，又可以分别描述为：

(1)均匀状态，即点态吸引子，或称不动点；

(2)简单的周期结构，即周期性吸引子，或称周期轨；

(3)混沌的非周期性模式，即混沌吸引子；

(4)这第四类行为可以与生命系统等复杂系统中的自组织现象相比拟，但在连续系统中没有相对应的模式。

但从研究元胞自动机的角度讲，最具研究价值的具有第四类行为的元胞自动机，因为这类元胞自动机被认为具有突现计算 Emergent Computation功能，研究表明，可以用作广义计算机 Universal Computer 以仿真任意复杂的计算过程。另外，此类元胞自动机在发展过程中还表现出很强的不可逆 Irreversibility 特征，而且，这种元胞自动机在若干有限循环后，有可能会 "死"掉，即所有元胞的状态变为零。


这是早期关于元胞自动机研究倾向于识别特定规则的模式类型，而沃尔弗拉姆的分类是首次尝试对规则本身进行分类。按照复杂程度的顺序，类别如下:
第1类: 几乎所有初始模式都迅速演变为稳定的均匀状态。初始模式中的任何随机性都会消失。[10]
第2类: 几乎所有初始模式都迅速演变为稳定或振荡的结构。初始模式中的某些随机性可能会被滤除，但仍然存在。初始模式的局部更改倾向于保持局部性质。[10]
第3类:几乎所有初始模式都以伪随机或混乱的方式演变。任何出现的稳定结构都会被周围的噪音迅速破坏。初始模式的局部更改趋向于无限期扩散。[10]
第4类: 几乎所有的初始模式都演变成以复杂而有趣的方式相互作用的结构，形成了可以长期存在的局部结构。[10]


第2类的稳定或振荡结构可能是最终的结果，即使初始模式相对简单，但达到这种状态可能需要很多步。初始模式的局部变化可能会无限扩散。沃尔弗拉姆推测存在很多第四类元胞自动机，即使不是全部，规则110和康威的生命游戏 Conway's Game of Life已经证明了这一点。


这些定义本质上是定性的，有一定解释空间。根据沃尔弗拉姆的说法：“...几乎所有的通用分类方案都是一种定义对应一个类别。 元胞自动机的分类也是如此: 偶尔会有一些规则来展示出一个类的某些特征和另一个类的某些特征。”[11]沃尔弗拉姆的分类是已根据经验与元胞自动机输出压缩长度的聚类相匹配而得出的。[26]


受沃尔弗拉姆分类法的启发，人们已多次尝试将元胞自动机以严格的形式分类。 例如，Culik 和 Yu 提出了三个具有明确定义的类(没有一种对应自动机的第四类)，这些类有时被称为 Culik-Yu 类; 这些类之间的关系已被证明是难以确定的。[27][28] [29] 沃尔弗拉姆的第2类可以划分为稳定(不动点)和具有振荡(周期)规则的两个子类。[30]


划分4类动力系统的想法最初来自诺贝尔化学奖获得者伊利亚·普里高津 Ilya Prigogine，他确定了热力学系统可划分为四类: (1)热力学平衡系统，(2)空间 / 时间均匀系统，(3)混沌系统，(4)具有耗散结构的复杂远离平衡系统。[31]


可逆的

主条目：可逆元胞自动机
如果对于元胞自动机的每个当前结构，恰好有一个过去的结构(原像)，则元胞自动机是可逆的。[32]如果我们把元胞自动机看作是从结构映射到结构的函数，那么可逆性就意味着这个函数是双射的。[32]如果元胞自动机是可逆的，那么其时间逆转行为也可以被描述为元胞自动机; 这个事实是Curtis-Hedlund-Lyndon定理的结果，该定理是元胞自动机的拓扑特征。[33][34]对于不是每个结构都有预映像的元胞自动机，这些没有预映像的结构称为初始模式。[6]


对于一维元胞自动机，已知有一些可以确定规则是否可逆的算法。[35][36] 然而，对于二维及更高维元胞自动机，其可逆性是无法判定的；换言之，没有一种以自动机规则作为输入，并保证正确地判断自动机是否可逆的算法。此定理由贾科·卡里 Jarkko Kari完成其证明，该证明与王浩平铺的拼贴问题有关。[37]


由于可逆的元胞自动机遵循热力学原理，因此可用于模拟诸如气体和流体动力学等物理现象。这种元胞自动机具有专门构造的可逆规则。托玛索·托佛利 Tommaso Toffoli，诺曼·马戈卢斯 Norman Margolus等人已经研究过这样的系统。有几种技术可以用来准确地构造具有已知的可逆元胞自动机。 常见的有二阶元胞自动机和分区元胞自动机，两者都是以某种方式修改元胞自动机的定义。虽然这种自动机并不严格满足上面给出的定义，但是它们可以由拥有足够大的邻域和状态数的传统元胞自动机来模拟，因此它们可以被认为是常规元胞自动机的子集。它们还证明了每一个可逆的元胞自动机都可以被一个分区元胞自动机模拟。[38][39]

完全的

一类特殊的元胞自动机是完全元胞自动机。完全元胞自动机中每个单元格的状态由一个数字表示(通常是从有限集合中提取的整数值)，t时刻的单元格取值仅取决于 t-1时刻邻近单元格取值的和(可能包括该单元格)。[11][10]如果 t 时刻的单元格状态取决于 t-1时刻的单元格状态和其邻近单元格状态的总和，那么称其为外部完全元胞自动机。[10]康威的生命游戏 Conway's Game of Life 就是一个外部完全元胞自动机的例子，其单元格取值为0和1; 外部完全元胞自动机的元胞自动机具有与生命相同的摩尔邻域结构，有时被称为仿生元胞自动机。[40]

相关的自动机

关于元胞自动机的概念有很多种概括。

基于六边形单元而不是正方形的元胞自动机


一种方法是不使用矩形(立方体等)网格。例如，一个平面以规则六边形作为单元格平铺。在许多情况下，产生的细胞自动机相当于具有特殊设计的邻域和规则的矩形网格。另一种方法是网格本身形状不规则，如彭罗斯平铺。[41]


同样，具有一定概率触发规则的元胞自动机称为随机元胞自动机。对于不同模式下的时间t，概率规则将给出中心单元格在时间t+1时转换为各种可能状态的概率。有时规则很简单，例如：“采取《康威的生命游戏 Conway's Game of Life》规则，但是在每个时间点上，每个单元格都有0.001％的概率会转变为相反的颜色。”


邻域或规则可能会随时间或空间的变化而变化。 例如，初始单元格的新状态可以由水平相邻的单元格确定，但对于下一代，将使用垂直单元格来确定其状态。


在元胞自动机中，一个单元格的新状态不受其他单元格的新状态影响。这也是可以改变的，例如，一个2×2的单元格块可以由它自己和邻近的单元格决定。


连续自动机像完全元胞自动机一样，但是规则和状态不是离散的（例如，使用状态{0,1,2}的表），而是使用连续函数，并且状态变为连续（通常为[0,1]中的值）。单个位置的状态是有限个实数。某些元胞自动机可以通过这种方式产生液体扩散。

组合自动机产生Sierpiński三角


连续空间自动机具有连续的位置和时间。单个位置的状态是有限个实数。状态根据微分方程式改变。一个重要的例子是反应-扩散纹理，这是艾伦·图灵 Alan Turing提出的用于解释化学反应如何在斑马和豹子身上形成条纹的微分方程。[42]当通过元胞自动机对其近似化时，它们通常会产生相似的模式。MacLennan[43]认为连续的空间自动机是一种计算模型。



有连续空间自动机的已知示例表现出类似于康威的生命游戏 Conway's Game of Life中的滑翔机的传播现象。[44]


图形再生自动机是基于图形再生系统的元胞自动机的扩展。[45]


组合自动机通过检查奇数/偶数索引对是否等于置换X来实现其功能。如果成立，则返回规则字符串的X（例如：“ 120012101”）。 这些元胞自动机与砖墙邻居 Brickwall_neighborhood 一起工作。 这些元胞自动机类型也像逻辑门 Logic gate一样起作用。 例如，当初始状态是单个居中单元格时，组合中的XOR 门的等效项将产生Sierpiński三角。

初等元胞自动机

3维动画演示一维元胞自动机产生下一代的规则

初等元胞自动机 Elementary Cellular Automata（ECA）的基本要素如下空间：

  • 一维直线上等间距的点。可为某区间上的整数点的集合。
  • 状态集：S={s1,s2} 即只有两种不同的状态。这两种不同的状态可将其分别编码为0 与 1；若用图形表示，则可对应“黑”与“白” 或者其他两种不同的颜色。
  • 邻居：取邻居半径r=1，即每个元胞最多只有“左邻右舍”两个邻居。
  • 演化规则：任意设定， 最多2^8=256种不同的设定方式。

元胞以相邻的8个元胞为邻居。即Moore邻居；一个元胞的生死由其在该时刻本身的生死状态和周围八个邻居的状态所决定。

最简单的元胞自动机是一维的，每个单元格具有两种状态，并且单元格的邻域定义为在其任一侧的相邻单元格。一个单元格及其两个相邻单元格形成一个3个单元格的邻域，因此邻域有23 = 8个可能的模式。规则包括为每种模式确定单元格在下一代中是1还是0。然后有28 = 256个可能的规则。 [46]


这256个元胞自动机通常由其Wolfram代码来引用，Wolfram代码是沃尔弗拉姆发明的标准命名规则，为每个规则赋予从0到255的数字。许多论文分析并比较了这256个元胞自动机。元胞自动机第30条和第110条规则非常有趣。下面的图像展示了由0包围的1(在每个图像的顶部)组成的初始结构的演变记录。每一行单元格表示自动机历史中的一代，其中t=0表示顶行。白色单元格表示0，黑色单元格表示1。


第30条元胞自动机规则

规则30
表格30.png


第30条元胞自动机规则表现出了第3类行为，这意味着即使是简单的输入模式（如所示）也会导致混乱的，看似随机的演变。


第110条元胞自动机规则

规则110
表格110.png


像《康威的生命游戏 Conway's Game of Life》一样，第110条元胞自动机规则表现出沃尔弗拉姆所称的第4类行为：它既不是完全随机的，也不是完全周期重复的。局部结构以各种看起来复杂的方式出现并相互作用。 马修·库克 Matthew Cook在1994年作为沃尔弗拉姆的研究助手在《一种新科学 a New Kind of Science》的发展过程中证明了其中一些结构足够丰富以支持图灵机的普遍性 Universal_Turing_machine 。这个结果很有趣，因为第110条元胞自动机规则是一个非常简单的一维系统，难以进行工程设计以执行特定行为。因此，该结果为沃尔弗拉姆的观点提供了重要的支持，即4类系统天生就具有普遍性。1998年，库克在圣塔菲研究所 Santa Fe Institute召开了有关元胞自动机的会议，但该证明被沃尔弗拉姆阻止在会议上提出，因为沃尔弗拉姆不想在《一种新科学 a New Kind of Science》出版之前公开证明。[47]因此,2004年，在库克提出该证明十年后，终于在沃尔弗拉姆的复杂系统 Complex Systems杂志（第15卷，第1期）上发表。第110条元胞自动机规则是一些最小型通用图灵机的基础。[48]

规则空间

初等元胞自动机规则由8位字符串指定，所有初等元胞自动机规则都可以视为定义在位于8维单元超立方体的顶点上。这个单元超立方体是元胞自动机规则空间。对于下一个近邻元胞自动机，规则由25 = 32位字符串指定，并且元胞自动机规则空间为32维单位超立方体。两个规则之间的距离可以通过沿着超立方体的边缘从一个顶点（代表第一条规则）和另一个顶点（代表另一条规则）移动所需的步数来定义。该距离也称为汉明距离。


元胞自动机规则空间让我们产生了以下问题：具有相似动态行为的规则是否彼此“接近”。在二维平面上以图形方式绘制高维超立方体仍然是一项艰巨的任务，超立方体中规则的粗定位器是基本规则的8位字符串中的bit-1(或次近邻规则的32位字符串)。在规则空间的这些切片中，在不同的沃尔弗拉姆类中绘制规则表明，第1类规则具有较少的bit-1，因此位于空间的一个区域中；而第3类规则具有比例更高的bit-1(50%)。[46]


对于较大的元胞自动机规则空间，第4类规则是第1类和第3类规则的过渡。[49]这一观察结果是混乱边缘这一阶段的基础，让人联想到热力学中的相变 Phase transition 。

生物学

元胞自动机可以模拟某些生物学发生过程。

贝壳的螺旋图案


一些贝壳的图案（如Conus和Cymbiola属的贝壳）是通过自然元胞自动机生成的。这些色素细胞沿着贝壳的边缘分布在一条狭窄的带子上。每个细胞遵循一个自然的数学规则,根据其邻近的色素细胞的激活和抑制活性分泌色素。[50] 当贝壳生长缓慢时，细胞带会在贝壳上留下彩色图案。例如，分布广泛的Conus textile的图案类似于沃尔弗拉姆第30条元胞自动机规则。[50]


植物通过元胞自动机机制调节气体的摄入和损失。叶子上的每个气孔都充当元胞。[51]


此外还有可以用两种状态的二维元胞自动机模拟头足类动物皮肤上的移动波型，每种状态都对应于扩展或缩回的色素细胞。


更有趣的是，人们发明了阈值自动机来模拟神经元的诸如识别和学习之类的复杂行为。[10]


还有研究发现，成纤维细胞与元胞自动机具有相似之处，因为每个成纤维细胞仅与其相邻细胞相互作用。[52]

化学类型

B-Z反应

Belousov-Zhabotinsky 反应(B-Z反应)是一个时空化学振荡器，可以用元胞自动机模拟。20世纪50年代，阿纳托尔·马尔科维奇·扎博丁斯基 Anatol Markovich Zhabotinsky（扩展了鲍里斯·帕夫洛维奇·别洛乌索夫 Boris Pavlovich Belousov的工作）发现，当一层薄薄的均匀的丙二酸、酸化溴酸盐和铈盐混合在一起并且不受干扰时，就形成了迷人的几何图案，如同同心圆和螺旋在介质中传播。此结果发表在1988年8月Scientific American杂志的“Computer Recreations”部分中，[53]此外亚历山大·基瓦丁·杜德尼 Alexander Keewatin Dewdney讨论了由德国比勒菲尔德大学的 Martin Gerhardt 和 Heike Schuster 开发的元胞自动机。[54]该自动机产生的波型类似于Belousov-Zhabotinsky反应中的波型。

应用程序

电脑处理器


元胞自动机处理器是元胞自动机概念的物理实现，可以在计算机上处理信息。处理单元以相同单元的规则网格排列。网格通常是二维正方形或三维的正方体拼贴或平铺。其他拼贴也是可能的，但尚未使用。单元状态仅通过与相邻单元的交互来确定，不存在直接与更远的单元进行通信。[55] 其中一个这样的元胞自动机处理器阵列配置就是脉冲阵列。元胞相互作用可以通过电荷，磁性，振动（声子（在量子尺度上)），或其他任何物理方式。因此任何单元之间不需要电线。这与当今大多数计算机（von Neumann设计）中使用的处理器截然不同，后者被划分为若干部分，这些部分可以通过线路与远距离的部分进行通信。

密码学


最初建议使用第30条元胞自动机规则作为可能密码学的分组密码。二维元胞自动机可用于构建伪随机数生成器。[56] 元胞自动机已被提出用于公钥加密。单向函数是一个有限元胞自动机的演化，其逆向元素很难找到。根据规则，任何人都可以轻易计算未来状态，但是很难计算历史状态。

纠错编码


Sen Gupta和P. Pal Chaudhuri在一篇论文中将元胞自动机应用于设计纠错码。这篇论文定义了一种使用元胞自动机构建单比特纠错和双比特错误检测（SEC-DED）码的新方案，并发布了一种用于该码的快速硬件解码器。[57]

建模物理现实

菱形十二面体是一个卡塔兰立体，有12个面、24条边和14个顶点，其中12面为12个全等的个菱形，且具有180度旋转对称性和点对称性，因此是一个环带多面体，其对偶多面体为截半立方体

正如安德鲁·伊拉钦斯基 Andrew Ilachinski 在元胞自动机中指出的那样，许多学者提出了宇宙是否是元胞自动机的问题。[10]Ilachinski认为，这个问题的重要性可以通过一个简单观察以便更好地理解。观察描述如下：思考元胞自动机第110条规则的演变过程：如果它是某种“外来物理学”，那么对观察到的模式的合理描述是什么？[10]如果观察者不知道图像是如何产生的，那么这个观察者最终可能会推测一些类似粒子的物体的运动。事实上，物理学家詹姆斯·克鲁奇菲尔德 James P. Crutchfield为其构建了一套严格的数学理论，证明了元胞自动机中‘’‘粒子’‘’在统计学上出现。[58]然后，随着争论的进行，有人可能会怀疑，在我们现有理解水平中，以粒子物理对象描述是合理的世界，在其基础的阶段是否可能是一个元胞自动机？这个基础阶段存在信息缺失问题，或者对于随机顺序出现的基础数据的理解不完全问题。这些可能与元胞自动机矛盾。
虽然还未发展出符合此思路的完整理论，但有趣的是，这一假设的提出使学者们对如何在一个离散的框架内理解我们的世界产生了有趣且丰富的猜测。人工智能的先驱马文·明斯基 Marvin Minsky研究了如何理解粒子与二维元胞自动机网格的相互作用。[59]最早的工作计算机Z3的发明者Konrad Zuse开发了一个不规则组织的网格，以解决粒子信息含量的问题。[60]最近，爱德华·弗雷德金Edward Fredkin揭示了他所说的“有限自然假说”，即“最终，物理学的每一个量，包括空间和时间，都将是离散的和有限的。”这一思想。[61]弗雷德金和斯蒂芬·沃尔夫勒姆 Stephen Wolfram是基于元胞自动机的物理学的有力支持者。2016年，杰拉德·霍夫特 Gerard't Hooft出版了一本书，详细介绍了利用细胞自动机重建量子力学的想法。[62]


近年来，非标准计算方面的文献也提出了其他建议。 沃尔弗拉姆的《一种新科学 a New Kind of Science》将元胞自动机视为理解包括物理在内的各种学科的关键。Ilabs创始人 Gabriele Rossi 与 Francesco Berto 和 Jacopo tagliabue 共同开发的参考模型数学，以一种新的“菱形十二面体”格子和独特规则为基础，展现了一个原始的二维/三维宇宙。这种模式满足普遍性（相当于图灵机）和完全可逆性（一个能满足人们想轻松地保存各种数量而又不丢失任何信息的迫切要求），并且将其套用到一阶理论中，从而对宇宙演化进行定量、定性描述。[63]

元胞自动机举例

生命游戏

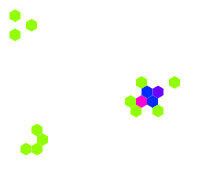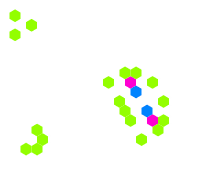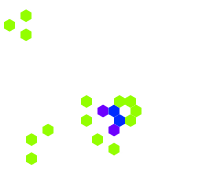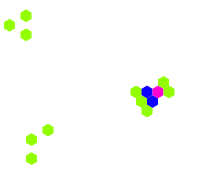
康威的生命游戏 Conway's Game of Life是英国数学家约翰·何顿·康威 John Horton Conway在1970年发明的元胞自动机。它最初于1970年10月由马丁·加德纳 Martin Gardner（1914年11月21日－2010年5月22日）发表在《科学美国人》杂志中的“数学游戏”专栏，该游戏从此名声大噪。

“滑翔机”：它会不断的产生一个有一个“滑翔者”，“滑翔者”：每4个回合它会延右下方移动一格，虽然细胞早就不是原来的细胞，但它能保持原来额形状

生命游戏是一种二维的元胞自动机，每个元胞都有黑白两种不同的状态，每个元胞都有周围八个方格作为邻居。生命游戏的规则如下：

  1. 当前细胞为存活状态时，当周围的存活细胞低于2个时（不包含2个），该细胞变成死亡状态。（模拟生命数量稀少）
  2. 当前细胞为存活状态时，当周围有2个或3个存活细胞时，该细胞保持原样。
  3. 当前细胞为存活状态时，当周围有超过3个存活细胞时，该细胞变成死亡状态。（模拟生命数量过多）
  4. 当前细胞为死亡状态时，当周围有3个存活细胞时，该细胞变成存活状态。（模拟繁殖）

当所有的元胞都按照这个规则检查它的邻居，并运行起来后，我们可以得到非常复杂的动态过程。

另外，生命游戏中还会诞生出一种被称为“滑翔机”的局部结构，它的动态运行情况如右图所示：

“滑翔机”可以作为一种局部传递信息的结构。可以利用“滑翔机”搭建更加复杂的动态结构。

一维基础元胞自动机

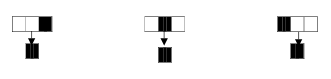
最简单的元胞自动机就是一维的元胞自动机。在其上，每个元胞都有黑、白两种颜色，每个元胞都有左右两个邻居。由于每个元胞有两个状态，这样，当前元胞加上左右两个邻居一共就有8种状态：

屏幕快照 2015-12-11 23.34.46.png

他们表示的状态分别是：000，001，010，011，100，101，110，111，其中0表示白色，1表示黑色。

下面考虑规则，由于元胞自动机的规则就是根据每个元胞和它的邻居的当前状态转移到下一个时刻该元胞的状态。无论规则是什么样的黑箱，它的输入就是上面列出的8种组合之一，因为表示的是每个元胞下一时刻的状态，而状态只可能有0、1两种，则规则的输出要么是0，要么是1。这样，任何一个规则都是一个或者一组转换，比如下图表示的就是一条规则：

屏幕快照 2015-12-11 23.36.07.png

另外，若有一个规则是：“如果输入的三个元胞中黑色方格只有1个，那么下一时刻当前元胞就是黑色”可以表示成下面的图：

屏幕快照 2015-12-11 23.36.54.png

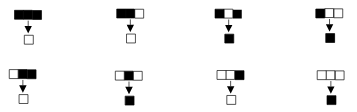
下面我们再把目光转到规则集上。由于每一条规则都是一个状态或一组状态的转换，那么把输入的8种可能情况转换到当前元胞的下一状态。我们可以用一个转换表表示一组规则集，例如：

屏幕快照 2015-12-11 23.37.37.png

这个规则集也可以用下面的一组数字表示为：

屏幕快照 2015-12-12 00.36.36.png

每一组规则集也可以表示成类似于上面的图和表，例如下面的另外一组规则

屏幕快照 2015-12-12 00.36.43.png

由于邻居加上当前元胞一共8种状态，每一个状态对应两种可能转换规则，所以规则一共就有[math]\displaystyle{ 2^8=256 }[/math]种，我们可以为每一个规则编码，然后对其进行穷举。

下面我们来考察这256中元胞自动机所具备的可能动态行为。对于一维的情况，我们假设所有的元胞都分布在一条直线上，并且直线的长度为300，也就是说有300个元胞在这条直线上，那么一条断续的横线就是当前所有细胞状态的一种分布。这些方格随着时间变化，就形成了不同的横线。我们把这些随着时间变化的线纵向拼在一起形成了一个网格区域。其中纵轴表示时间的流逝（往下为正），横轴为“元胞自动机在对应时刻的状态，就能得到一幅图像：

屏幕快照 2015-12-12 00.42.38.png

这个元胞的每一行都是某一个时刻元胞自动机的状态。因而从上到下数第1、2、3、4、5、6行可以分别表示第1、2、3、4、5、6时间步的元胞自动机状态。因此这里的一个平面的图案就是元胞自动机在时间上的发展动态。下面我们分别挑选几种典型的动态情况示于下图（下方的数字是元胞自动机的编码）：

屏幕快照 2015-12-12 00.42.44.png

屏幕快照 2015-12-12 00.44.21.png

  • CA 00：184号

  • CA 01：250号

  • CA 02：254号

  • CA 03：300号

NaSch模型

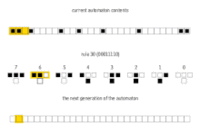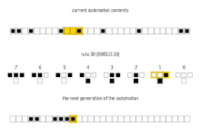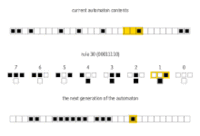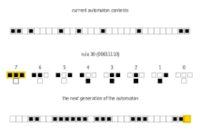
1992年，德国学者 Nagel 和 Schreckenberg 在第184号元胞自动机规则的基础上提出了一维交通流CA模型，即，NS 模型（或NaSch模型）。[64]

NS模型.png

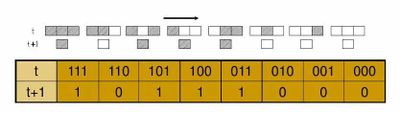
184规则模拟交通流（1表示有车，0表示无车，并且每辆车只在其前面具有开放空间时（前面一个格子为 0）才向前移动。这里前方定义为格子的右向）。

在其演化的每个步骤中，184规则自动机同时对所有细胞使用以下规则生成下一个阵列中的每个细胞，以确定每个细胞的新状态：

Swarma10-1547211614.jpeg

NaSch 模型是一个交通流模型，每辆车的状态都由它的速度和位置所表示，其状态按照以下演化规则并行更新。

NS模型的规则如下：

  • 加速过程：[math]\displaystyle{ {v_n \rightarrow min(v_n+1, v_{max})} }[/math]，如果车辆的速度低于最大速度，且前方有空余的空间，那么在下一个时刻，速度会增加1。
  • 减速过程：[math]\displaystyle{ {v_n \rightarrow min(v_n, d_n)} }[/math]，如果车辆发现前方在某一确定距离内有其他车辆，并且这个距离要小于它的速度，那么车辆的速度会减少。
  • 随机慢化：以概率[math]\displaystyle{ {p} }[/math]，[math]\displaystyle{ {v_n \rightarrow max(v_n-1, 0)} }[/math]，由各种不确定因素，会导致车辆的速度减1，速度不低于零。
  • 位置更新：[math]\displaystyle{ {x_n \rightarrow x_n+v_n } }[/math]，车辆按照预定的方式前进。


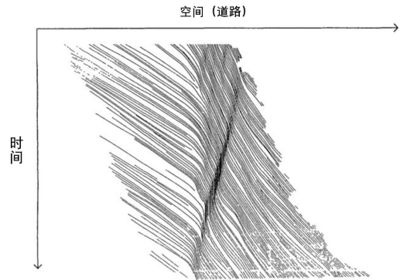
NaSch模型的效果展示:

纵轴是时间轴，横轴是在某一时刻的路况情况。发现随着时间的推移，原本没有堵塞情况的路况会自动出现堵塞，并且拥堵情况会在道路上传递
用NaSch模型模拟得到的车辆运动时空图（车辆从左往右移动，从上到下为时间演化方向）


参考文献

  1. ↑ 1.0 1.1 Wolfram, Stephen (1983) "Statistical Mechanics of Cellular Automata".Reviews of Modern Physics.55.(601--644)
  2. ↑ Tommaso; Margolus Norman, Toffoli (1987) "Cellular Automata Machines: A New Environment for Modeling".27.
  3. ↑ Schiff, Joel L (2011) "Cellular Automata: A Discrete View of the World".(40)
  4. ↑ 4.0 4.1 Kier, Lemont B.; Seybold, Paul G.; Cheng, Chao-Kun (2005). Modeling Chemical Systems using Cellular Automata. Springer. ISBN 9781402036576.
  5. ↑ Bialynicki-Birula, Iwo; Bialynicka-Birula, Iwona (2004). Modeling Reality: How Computers Mirror Life. Oxford University Press. ISBN 978-0198531005.
  6. ↑ 6.0 6.1 6.2 6.3 6.4 Schiff, Joel L. (2011). Cellular Automata: A Discrete View of the World. Wiley & Sons, Inc. p. 40. ISBN 9781118030639.
  7. ↑ Pickover, Clifford A. (2009). The Math Book: From Pythagoras to the 57th Dimension, 250 Milestones in the History of Mathematics. Sterling Publishing Company, Inc. p. 406. ISBN 978-1402757969.
  8. ↑ John von Neumann, "The general and logical theory of automata," in L.A. Jeffress, ed., Cerebral Mechanisms in Behavior – The Hixon Symposium, John Wiley & Sons, New York, 1951, pp. 1–31.
  9. ↑ Kemeny, John G. (1955). "Man viewed as a machine". Sci. Am. 192 (4): 58–67. Bibcode:1955SciAm.192d..58K. doi:10.1038/scientificamerican0455-58.; Sci. Am. 1955; 192:6 (errata)
  10. ↑ 10.00 10.01 10.02 10.03 10.04 10.05 10.06 10.07 10.08 10.09 10.10 Ilachinski, Andrew (2001). Cellular Automata: A Discrete Universe. World Scientific. ISBN 9789812381835.
  11. ↑ 11.00 11.01 11.02 11.03 11.04 11.05 11.06 11.07 11.08 11.09 11.10 Wolfram, Stephen (2002). A New Kind of Science. Wolfram Media. ISBN 978-1579550080.
  12. ↑ von Neumann, John; Burks, Arthur W. (1966). Theory of Self-Reproducing Automata. University of Illinois Press.
  13. ↑ 13.0 13.1 Wiener, N.; Rosenblueth, A. (1946). "The mathematical formulation of the problem of conduction of impulses in a network of connected excitable elements, specifically in cardiac muscle". Arch. Inst. Cardiol. México. 16: 205.
  14. ↑ Letichevskii, A. A.; Reshodko, L. V. (1974). "N. Wiener's theory of the activity of excitable media". Cybernetics. 8 (5): 856–864. doi:10.1007/bf01068458.
  15. ↑ Davidenko, J. M.; Pertsov, A. V.; Salomonsz, R.; Baxter, W.; Jalife, J. (1992). "Stationary and drifting spiral waves of excitation in isolated cardiac muscle". Nature. 355 (6358): 349–351. Bibcode:1992Natur.355..349D. doi:10.1038/355349a0. PMID 1731248.
  16. ↑ Hedlund, G. A. (1969). "Endomorphisms and automorphisms of the shift dynamical system". Math. Systems Theory. 3 (4): 320–3751. doi:10.1007/BF01691062.
  17. ↑ Smith, Alvy Ray. "Cellular Automata Complexity Trade-Offs" (PDF). {{cite journal}}: Cite journal requires |journal= (help)
  18. ↑ Smith, Alvy Ray. "Simple Computation-Universal Cellular Spaces" (PDF). {{cite journal}}: Cite journal requires |journal= (help)
  19. ↑ Smith, Alvy Ray. "Simple Nontrivial Self-Reproducing Machines" (PDF). {{cite journal}}: Cite journal requires |journal= (help)
  20. ↑ Smith, Alvy Ray. "Introduction to and Survey of Cellular Automata or Polyautomata Theory" (PDF). {{cite journal}}: Cite journal requires |journal= (help)
  21. ↑ Gardner, Martin (1970). ""Mathematical Games: The fantastic combinations of John Conway's new solitaire game "life"". Scientific American. 223 (223): 601–644.
  22. ↑ Paul Chapman (2002). ""Life Universal Computer"". Life universal computer.
  23. ↑ Mitchell, Melanie (4 October 2002). "Is the Universe a Universal Computer?". Science. 298 (5591): 65–68. doi:10.1126/science.1075073.
  24. ↑ Johnson, George (2002). ""'A New Kind of Science': You Know That Space-Time Thing? Never Mind". The New York Times.
  25. ↑ "The Science of Everything". The Economist. 2002.
  26. ↑ Zenil, Hector (2010). "Compression-based investigation of the dynamical properties of cellular automata and other systems" (PDF). Complex Systems. 19 (1).
  27. ↑ G. Cattaneo; E. Formenti; L. Margara (1998). "Topological chaos and CA". In M. Delorme; J. Mazoyer (eds.). Cellular automata: a parallel model. Springer. p. 239. ISBN 978-0-7923-5493-2.
  28. ↑ Burton H. Voorhees (1996). Computational analysis of one-dimensional cellular automata.. World Scientific. pp. 8. 
  29. ↑ Max Garzon (1995). Models of massive parallelism: analysis of cellular automata and neural networks. Springer. p. 149. ISBN 978-3-540-56149-1.
  30. ↑ Li, Wentian; Packard, Norman (1990). "The structure of the elementary cellular automata rule space" (PDF). Complex Systems. 4: 281–297.
  31. ↑ Nicolis (1974). "Dissipative Structures, Catastrophes, and Pattern Formation: A Bifurcation Analysis" (PDF). PNAS. 71 (7): 2748–2751.
  32. ↑ 32.0 32.1 Gutowitz, Howard, ed. (1991). Cellular Automata: Theory and Experiment. MIT Press. ISBN 9780262570862.
  33. ↑ Richardson, D. (1972). "Tessellations with local transformations". J. Computer System Sci. 6 (5): 373–388. doi:10.1016/S0022-0000(72)80009-6.
  34. ↑ Margenstern, Maurice (2007). Cellular Automata in Hyperbolic Spaces – Tome I, Volume 1. Archives contemporaines. p. 134. ISBN 978-2-84703-033-4.
  35. ↑ Amoroso, Serafino; Patt, Yale N. (1972). "Decision Procedures for Surjectivity and Injectivity of Parallel Maps for Tessellation Structures". J. Comput. Syst. Sci. 6 (5): 448–464. doi:10.1016/s0022-0000(72)80013-8.
  36. ↑ Sutner, Klaus (1991). "De Bruijn Graphs and Linear Cellular Automata" (PDF). Complex Systems. 5: 19–30.
  37. ↑ Kari, Jarkko (1990). "Reversibility of 2D cellular automata is undecidable". Physica D. 45 (1–3): 379–385. Bibcode:1990PhyD...45..379K. doi:10.1016/0167-2789(90)90195-U.
  38. ↑ Kari, Jarkko (1999). "On the circuit depth of structurally reversible cellular automata". Fundamenta Informaticae. 38: 93–107.
  39. ↑ Durand-Lose, Jérôme (2001). "Representing reversible cellular automata with reversible block cellular automata". Discrete Mathematics and Theoretical Computer Science. AA: 145–154. Archived from the original on 15 May 2011.
  40. ↑ The phrase "life-like cellular automaton" dates back at least to Barral, Chaté & Manneville (1992), who used it in a broader sense to refer to outer totalistic automata, not necessarily of two dimensions. The more specific meaning given here was used e.g. in several chapters of Adamatzky (2010). See: Barral, Bernard; Chaté, Hugues; Manneville, Paul (1992). "Collective behaviors in a family of high-dimensional cellular automata". Physics Letters A. 163 (4): 279–285. Bibcode:1992PhLA..163..279B. doi:10.1016/0375-9601(92)91013-H.
  41. ↑ Jacob Aron. "First gliders navigate ever-changing Penrose universe". New Scientist.
  42. ↑ JMurray, J. "Mathematical Biology II". Springer.
  43. ↑ http://web.eecs.utk.edu/~bmaclenn/contin-comp.html
  44. ↑ Pivato, M: "RealLife: The continuum limit of Larger than Life cellular automata", Theoretical Computer Science, 372 (1), March 2007, pp. 46–68
  45. ↑ Tomita, Kohji; Haruhisa Kurokawa; Satoshi Murata (2009). "Graph-rewriting automata as a natural extension of cellular automata". Adaptive Networks. Springer: 291–309.
  46. ↑ Bialynicki-Birula, Iwo; Bialynicka-Birula, Iwona (2004). Modeling Reality: How Computers Mirror Life. Oxford University Press. ISBN 978-0198531005.
  47. ↑ Giles, Jim (2002). "What Kind of Science is This?". Nature. 417 (6886): 216–218. Bibcode:2002Natur.417..216G. doi:10.1038/417216a. PMID 12015565.
  48. ↑ Weinberg, Steven. "Is the Universe a Computer?". The New York Review of Books.
  49. ↑ Wentian Li; Norman Packard; Chris G Langton (1990). "Transition phenomena in cellular automata rule space". Physica D. 45 (1–3): 77–94. Bibcode:1990PhyD...45...77L. CiteSeerX 10.1.1.15.2786. doi:10.1016/0167-2789(90)90175-O.
  50. ↑ 50.0 50.1 Coombs, Stephen (2009). "The Geometry and Pigmentation of Seashells" (PDF). {{cite journal}}: Cite journal requires |journal= (help)
  51. ↑ Peak, West; Messinger, Mott (2004). "Evidence for complex, collective dynamics and emergent, distributed computation in plants". Proceedings of the National Academy of Sciences. 101 (4): 918–922.
  52. ↑ Yves Bouligand (1986). Disordered Systems and Biological Organization. pp. 374–375.
  53. ↑ A. K. Dewdney, The hodgepodge machine makes waves, Scientific American, p. 104, August 1988.
  54. ↑ Gerhardt, M.; Schuster, H. (1989). "A cellular automaton describing the formation of spatially ordered structures in chemical systems". Physica D. 36 (3): 209–221. Bibcode:1989PhyD...36..209G. doi:10.1016/0167-2789(89)90081-x.
  55. ↑ Muhtaroglu, Ali (August 1996). "4.1 Cellular Automaton Processor (CAP)". Cellular Automaton Processor Based Systems for Genetic Sequence Comparison/Database Searching. Cornell University. pp. 62–74.
  56. ↑ Tomassini, M.; Sipper, M.; Perrenoud, M. (2000). "On the generation of high-quality random numbers by two-dimensional cellular automata". IEEE Transactions on Computers. 49 (10): 1146–1151. doi:10.1109/12.888056.
  57. ↑ Chowdhury, D. Roy; Basu, S.; Gupta, I. Sen; Chaudhuri, P. Pal (June 1994). "Design of CAECC - cellular automata based error correcting code". IEEE Transactions on Computers. 43 (6): 759–764. doi:10.1109/12.286310.
  58. ↑ J. P. Crutchfield, (1994). "The Calculi of Emergence: Computation, Dynamics, and Induction" (PDF). Physica.D.{{cite journal}}: CS1 maint: extra punctuation (link)
  59. ↑ Minsky, M. (1982). "Cellular Vacuum". International Journal of Theoretical Physics. 21 (537–551): 1982. Bibcode:1982IJTP...21..537M. doi:10.1007/bf02650183.
  60. ↑ K. Zuse, "The Computing Universe", Int. Jour. of Theo. Phy. 21, 589–600, 1982.
  61. ↑ E. Fredkin, "Digital mechanics: an informational process based on reversible universal cellular automata", Physica D 45, 254–270, 1990
  62. ↑ Gerard 't Hooft, 2016, The Cellular Automaton Interpretation of Quantum Mechanics, Springer International Publishing, DOI 10.1007/978-3-319-41285-6, Open access-[1]
  63. ↑ F. Berto, G. Rossi, J. Tagliabue, The Mathematics of the Models of Reference, College Publications, 2010
  64. ↑ Nagel, K., & Schreckenberg, M. (1992). A cellular automaton model for freeway traffic Kai Nagel, Michael Schreckenberg. Journal de physique I, 2(12), 2221-2229.

推荐文献

  1. von Neumann, John; Burks, Arthur W. (1966). Theory of Self-Reproducing Automata. University of Illinois Press.
  2. Gardner, Martin (1970). "Mathematical Games: The fantastic combinations of John Conway's new solitaire game "life"". Scientific American (223): 120–123.
  3. Wolfram, Stephen (1983). "Statistical Mechanics of Cellular Automata". Reviews of Modern Physics. 55 (3): 601–644.
  4. Gutowitz, Howard, ed. (1991). Cellular Automata: Theory and Experiment. MIT Press.
  5. Ilachinski, Andrew (2001). Cellular automata: a discrete universe. World Scientific. pp. 44–45.
  6. Wolfram, Stephen (2002). A New Kind of Science. Wolfram Media. ISBN 978-1579550080.

相关词条

在集智百科上，跟元胞自动机主题相关的词条：

  • 方格宇宙，这是张江老师分享的从另一个角度，解析元胞自动机，一探方格宇宙的奥秘。
  • 朗顿的蚂蚁也是元胞自动机的一个例子，由克里斯托弗·朗顿 Christopher Langton，在该词条内有详细的介绍和对应的代码演示。

相关链接

知乎：简单明了的讲解一下元胞自动机及其应用？

知乎：3-单车道元胞自动机的NaSch模型

编者推荐

针对元胞自动机的情况，整理一些国内的资源，推荐给大家：

  • 北京师范大学张江老师为北师大新入学的新生，设计的一门上手编程，亲手设计元胞自动机的教程《NetLogo多主体建模》，非常简洁易懂，容易上手，可以非常容易的就自己实现一个元胞自动机。关于元胞自动机的原理性介绍，可以看张江老师的公开课：认识元胞自动机。
  • 清华大学龙瀛老师在城市建模概论中专门有一个是分享元胞自动机建模的内容。


本中文词条由费米子编辑，欢迎在讨论页面留言。

本词条内容源自wikipedia及公开资料，遵守 CC3.0协议。

取自“https://wiki.swarma.org/index.php?title=元胞自动机&oldid=3890”