基于格兰杰因果量化涌现
简介
涌现(emergence)在人工生命和复杂性科学中至关重要。然而目前关于涌现的定量、直观且易于应用的测量方法却极为匮乏。本文提出了一种名为“G-涌现”(G-emergence)的新测量方法,它将涌现过程“既受到底层因果因素的影响,同时又具备自身独立性”的这一概念进行了具体化和应用。G-涌现基于“格兰杰因果关系”的非线性时间序列分析,能够同时衡量涌现现象和明显的向下因果 (downward causation)。我通过一个经典的涌现实例——基于智能体(Agent)的鸟群模拟来展示这一方法的应用,并探讨了它对科学中最具挑战性的涌现问题之一的意识问题可能产生的深远影响。
近年来,随着人工生命和复杂性科学的发展,人们对涌现现象重新产生了兴趣。虽然涌现的概念有着悠久的哲学历史[1][2],其核心思想其实非常简单:一种涌现的属性通常是“整体大于部分的总和”。在各类复杂系统中,涌现属性非常普遍,比如在生物系统、认知系统、社会系统和技术系统中。总体来说,人工生命和复杂性科学主要是解释看似与涌现相关的现象,而这些领域中的模型通常被描述为具有涌现性质[3]。因此,令人惊讶且值得注意的是,目前缺乏定量且易于应用的涌现测量方法。而这很可惜,因为科学上对现象的有效描述很大程度上依赖于是否能对其进行测量[4]。
在本文中,我将首先区分几种涌现的概念,并借此简要说明其中的一些关键挑战。接着,我将介绍一种名为“G-涌现”(G-emergence)的新测量方法,这种方法具体化了一个直观的想法,即涌现过程既独立于其底层因果因素,同时又依赖于这些因素。G-涌现简单易用,我会通过一个经典的涌现现象例子——鸟群飞行的模拟来展示这一方法的应用(下图是一群即将栖息的椋鸟)。最后,我将讨论相关的测量方法,如何化解“向下因果”(downward causation)这一形而上学上的难题,以及它如何为科学中最难解决的问题之一的神经机制与现象体验之间的关系带来新的启示。
涌现的类型
从直观上看,涌现可以指两种情况:一种是宏观层面的属性,它“超越了微观部分的总和”(称为“属性涌现”或“共时涌现”,property/synchronic emergence);另一种是随着时间推移,出现了某种全新的、有质的区别的现象(称为“时间涌现”或“历时涌现”,temporal/diachronic emergence)。一个属性涌现的典型例子是当鸟群在天空中飞行时,鸟群似乎拥有独立的形状和轨迹,远远超越了每只鸟的个体行为。历时涌现的典型例子则可以从胚胎发育过程中,新形态特征逐渐形成的过程看出。本文主要探讨如何衡量属性涌现,但也指出了衡量时间涌现的潜在机会。根据 Bedau[5][3]的分类,属性涌现和时间涌现都可以进一步划分为三类:强涌现(strong emergence)、弱涌现(weak emergence)和名义涌现(nominal emergence)。
名义涌现
最不具争议性的是名义涌现,它指的是一种宏观层面的属性,虽然它存在于宏观对象或过程之中,但在微观层面是没有的。例如,一个圆是由一组点构成的,但圆这个属性是这些点在宏观层面的涌现,因为它不能简单地从每个点中得到。由于名义涌现的推导非常简单,本文不再详细讨论。
强涌现
最具挑战性和争议性的是强涌现,它包括两个密切相关的观点。首先,宏观层面的属性原则上无法从微观层面的观察中辨别出来。其次,宏观层面的属性具有不可还原的因果力量。第一个观点完全否定了机械论解释的可能性,似乎意味着如果没有新的自然基本原理,科学的进展将停止[6]。第二个观点引发了“向下因果作用”(downward causation)这一复杂概念。向下因果作用的问题在于,它违背了“宏观的存在方式是由微观决定的”这一合理理论,这一理论被称为“因果基础论”(causal fundamentalism)[7]或“附属性”(supervenience)[2]。此外,向下因果作用还带来另一个挑战,即如何解决微观层面与宏观层面之间的因果冲突[3]。即便如此,强涌现最大的挑战可能在于其在科学上的不重要性[3]。目前科学文献中唯一反复出现的强涌现例子是意识状态(如感质,qualia)从神经生物过程中的涌现[8][6],这更多地说明我们对意识的理解不足,而非对涌现深层原理的掌握有限。后文将进一步探讨这一可能性。
弱涌现
弱涌现的概念介于强涌现和名义涌现之间[5][3]。在弱涌现中,宏观层面的属性来源于微观层面组成部分的相互作用,但这种相互作用非常复杂,以至于宏观属性无法简单地通过微观解释来得出。与强涌现不同,弱涌现的宏观属性原则上是可以从微观层面辨别出来的;与名义涌现不同,微观到宏观的推理路径并不简单。据 Bedau 所述,弱涌现的宏观属性在本体上依赖于并可还原为微观因果因素,但由于微观到宏观的推导路径复杂,导致在认识上无法轻易还原。
那么,宏观属性在认识上不可还原是什么意思呢?Bedau 的回答是,弱涌现的(在认识上不可还原的)属性只有通过模拟才能推导出来。这是一种非此即彼的分类:要么宏观属性可以通过某种解释捷径推导出来,此时弱涌现不适用;要么无法推导,此时必须明确模拟微观因果因素来得出宏观属性。
本文提出了一个连续的弱涌现版本,认为宏观属性在多大程度上无法从微观层面观察中辨别,决定了其弱涌现的程度。这种变化之所以有价值,首先是因为对于许多系统来说,证明“只能通过模拟推导”可能并不现实;其次,从测量的角度来看,连续值比二元分类更有用。
格兰杰涌现(G-涌现)方法
为了得出一种连续的弱涌现的测量方法,我从一个基本概念开始:一个弱涌现的宏观属性同时具备(i) 自主性和(ii) 对其底层因果因素的依赖性[5]。为了将这一概念转化为统计学上的操作方法,我提出可以通过如下方式来衡量一个宏观变量[math]\displaystyle{ M }[/math]相对于一组微观变量[math]\displaystyle{ m }[/math](其中 [math]\displaystyle{ (m = m_1, m_2, ..., m_N) }[/math])的弱涌现程度:条件1:[math]\displaystyle{ M }[/math]的过去观测值能够比仅基于[math]\displaystyle{ m }[/math]的过去观测值更准确地预测[math]\displaystyle{ M }[/math]的未来观测值。条件2:[math]\displaystyle{ m }[/math]的过去观测值能够比仅基于[math]\displaystyle{ M }[/math]的过去观测值更准确地预测M的未来观测值。
第一个条件提供了一个客观的度量标准,来衡量从微观到宏观的推导路径是否具有非平凡性;第二个条件则检验了从微观到宏观的因果依赖性。这个定义依赖于宏观和微观描述层次的选择,同时也依赖于预测方法的选择。正如后文所述,格兰杰[9]最早提出的因果关系的统计定义,为这种预测提供了适当的框架,因此本文将这种测量方法称为G-涌现(G-emergence)。
格兰杰因果测量
1969年,Granger提出了“格兰杰因果”(Granger causality,简称G-causality)的概念,这是对Wiener直觉的形式化表达。Wiener的直觉是,如果知道变量[math]\displaystyle{ Y }[/math]有助于预测变量[math]\displaystyle{ X }[/math]的未来,那么我们就可以说[math]\displaystyle{ Y }[/math]“导致”了[math]\displaystyle{ X }[/math][9][10]。根据格兰杰因果关系,如果在一个包含[math]\displaystyle{ X }[/math]和[math]\displaystyle{ Y }[/math]的线性回归模型中,加入的[math]\displaystyle{ Y }[/math]过去观测值能够减少[math]\displaystyle{ X }[/math]的预测误差,相比于仅使用[math]\displaystyle{ X }[/math]的过去观测值的模型,那么可以被认为[math]\displaystyle{ Y }[/math]是导致了[math]\displaystyle{ X }[/math]。
自提出以来,格兰杰因果关系已广泛应用于经济学及其他领域,如神经科学和气候学[11] [12]。为说明格兰杰因果关系,假设有两个时间序列[math]\displaystyle{ X_1(t) }[/math]和[math]\displaystyle{ X_2(t) }[/math]时间长度均为[math]\displaystyle{ t }[/math],它们的时间动态可以用一个双变量自回归模型来描述。
[math]\displaystyle{ \begin{align*} X_1(t) &= \sum_{j=1}^{p} A_{11,j} X_1(t - j) + \sum_{j=1}^{p} A_{12,j} X_2(t - j) + \xi_1(t) \\ X_2(t) &= \sum_{j=1}^{p} A_{21,j} X_1(t - j) + \sum_{j=1}^{p} A_{22,j} X_2(t - j) + \xi_2(t) \end{align*} }[/math]
其中,[math]\displaystyle{ p }[/math] 是模型中包含的最大滞后观测值的数量(即模型的阶数,[math]\displaystyle{ p \lt T }[/math]),表示过去 [math]\displaystyle{ p }[/math] 个时间点的观测值将被纳入模型。[math]\displaystyle{ j }[/math] 是一个索引变量,表示每个滞后步长(从 [math]\displaystyle{ 1 }[/math] 到 [math]\displaystyle{ p }[/math]),在每个时间点上依次考虑的过去观测值。[math]\displaystyle{ A_{11,j} }[/math]、[math]\displaystyle{ A_{12,j} }[/math]、[math]\displaystyle{ A_{21,j} }[/math] 和 [math]\displaystyle{ A_{22,j} }[/math] 是自回归模型中的系数,表示每个滞后步长 [math]\displaystyle{ j }[/math] 对相应变量的影响强度,这些系数是模型学习得到的参数,用于描述不同滞后项的影响。[math]\displaystyle{ X_1(t - j) }[/math] 和 [math]\displaystyle{ X_2(t - j) }[/math] 分别表示时间 [math]\displaystyle{ t - j }[/math] 时刻的变量 [math]\displaystyle{ X_1 }[/math] 和 [math]\displaystyle{ X_2 }[/math] 的值,用于反映过去 [math]\displaystyle{ j }[/math] 个时间步长对当前值的影响。[math]\displaystyle{ \xi_1(t) }[/math] 和 [math]\displaystyle{ \xi_2(t) }[/math] 是每个时间序列的残差(或预测误差),表示模型未能解释的部分。如果在第一个(或第二个)方程中引入 [math]\displaystyle{ X_2 }[/math](或 [math]\displaystyle{ X_1 }[/math])项后,[math]\displaystyle{ \xi_1 }[/math](或 [math]\displaystyle{ \xi_2 }[/math])的方差减小,那么可以说 [math]\displaystyle{ X_2 }[/math](或 [math]\displaystyle{ X_1 }[/math])对 [math]\displaystyle{ X_1 }[/math](或 [math]\displaystyle{ X_2 }[/math])具有格兰杰因果性。
假设[math]\displaystyle{ X_1 }[/math]和[math]\displaystyle{ X_2 }[/math]是协方差平稳的(即它们的均值和方差不随时间变化),那么这种相互作用的大小可以通过受限模型([math]\displaystyle{ R }[/math])和非受限模型([math]\displaystyle{ U }[/math])预测误差方差的对数比率来衡量:
[math]\displaystyle{ gc_{2 \to 1} = \log \left( \frac{\mathrm{var}(\xi_{1R(12)})}{\mathrm{var}(\xi_{1U})} \right), }[/math]
其中,[math]\displaystyle{ gc_{2 \to 1} }[/math] 表示从变量 [math]\displaystyle{ X_2 }[/math] 到变量 [math]\displaystyle{ X_1 }[/math] 的格兰杰因果性测量值。[math]\displaystyle{ \xi_{1R(12)} }[/math] 是从省略了是从省略了第一个方程中的 [math]\displaystyle{ A_{12,j} }[/math](对所有 [math]\displaystyle{ j }[/math])系数的模型中得到的预测误差;[math]\displaystyle{ \xi_{1U} }[/math] 是从包含 [math]\displaystyle{ X_2 }[/math] 对 [math]\displaystyle{ X_1 }[/math] 影响的完整模型中得到的预测误差。通过计算 [math]\displaystyle{ \frac{\text{var}(\xi_{1R(12)})}{\text{var}(\xi_{1U})} }[/math] 的对数,[math]\displaystyle{ gc_{2 \to 1} }[/math] 可以量化 [math]\displaystyle{ X_2 }[/math] 对 [math]\displaystyle{ X_1 }[/math] 的预测贡献。如果 [math]\displaystyle{ gc_{2 \to 1} }[/math] 的值为正,说明包含 [math]\displaystyle{ X_2 }[/math] 能显著减少 [math]\displaystyle{ X_1 }[/math] 的预测误差,表明 [math]\displaystyle{ X_2 }[/math] 对 [math]\displaystyle{ X_1 }[/math] 有格兰杰因果性。重要的是,格兰杰因果关系很容易推广到多变量的情况,在这种情况下,检验的是在多个变量[math]\displaystyle{ X₂...Xₙ }[/math]的上下文中的格兰杰因果关系(对所有 [math]\displaystyle{ Xᵢ ≠ Xⱼ }[/math])。在这种情况下,如果当所有其他变量 [math]\displaystyle{ X₃...Xₙ }[/math] 的活动也包含在回归模型中时,知道 [math]\displaystyle{ X₂ }[/math] 会减少[math]\displaystyle{ X₁ }[/math] 预测误差的方差,那么[math]\displaystyle{ X₂ }[/math]对[math]\displaystyle{ X₁ }[/math]具有格兰杰因果性(参见下文)。有关格兰杰因果关系的教程介绍,请参阅 Seth[10]。
格兰杰自主性测量
格兰杰因果关系的一个简单扩展允许对变量相对于其他变量集的“统计自主性”进行量化[13]。在这种情况下,我们不是询问通过包括 的过去观测是否减少了 的预测误差,而是询问在给定一组外部变量的情况下,通过包括自身的过去是否减少了它的预测误差。也就是说,变量的格兰杰自主性体现在其自身的过去状态在基于一组外部变量的过去状态的预测之外,是否有助于预测其未来状态。与格兰杰因果关系类似,相对于的格兰杰自主性定义为:
[math]\displaystyle{ ga_{X_1 | X_2} = \log \left( \frac{\mathrm{var}(\xi_{1R(11)})}{\mathrm{var}(\xi_{1U})} \right), }[/math]
其中,[math]\displaystyle{ ga_{X_1 | X_2} }[/math] 表示变量 [math]\displaystyle{ X_1 }[/math] 相对于变量 [math]\displaystyle{ X_2 }[/math] 的格兰杰自主性。它通过计算两种情况下的预测误差方差的对数比率来衡量,即在不包含 [math]\displaystyle{ X_1 }[/math] 过去信息的受限模型(仅使用 [math]\displaystyle{ X_2 }[/math] 的信息)和包含 [math]\displaystyle{ X_1 }[/math] 过去信息的完整模型之间的差异。如果 [math]\displaystyle{ ga_{X_1 | X_2} }[/math] 值为正,表示 [math]\displaystyle{ X_1 }[/math] 的过去状态对预测其未来状态有显著贡献,体现了 [math]\displaystyle{ X_1 }[/math] 的统计自主性。[math]\displaystyle{ \xi_{1R(11)} }[/math] 是从省略了 [math]\displaystyle{ A_{11,j} }[/math](对所有 [math]\displaystyle{ j }[/math])系数的受限模型中得到的预测误差,而 [math]\displaystyle{ \xi_{1U} }[/math] 是从完整模型中得到的预测误差。
格兰杰自主性放大了“自我决定”这一自主性概念,与其他更为抽象的概念(如“组织封闭性”[14])形成对比。它与这样一种观点相一致,即(在行为上)自主的系统不应完全由其环境决定,且随机系统不应具有高度自主性 [15]。简而言之,变量的格兰杰自主性在于它依赖于自身的历史,而这些依赖关系不能通过外部因素来解释。之前我已表明,格兰杰自主性在简单模型系统中表现符合预期,并且可以作为进化适应的结果而增加[13]。
线性格兰杰涌现测量
在定义了格兰杰因果和格兰杰自主性之后,扩展到格兰杰涌现是直接的。当且仅当[math]\displaystyle{ M }[/math]对一组微观变量[math]\displaystyle{ m }[/math]是格兰杰自主的,且[math]\displaystyle{ M }[/math]由[math]\displaystyle{ m }[/math]引起时,宏观变量[math]\displaystyle{ M }[/math]被认为是从一组微观变量[math]\displaystyle{ m }[/math]中涌现的。因此,衡量[math]\displaystyle{ M }[/math]从[math]\displaystyle{ m }[/math]中的格兰杰涌现性的一个简单方法为:
[math]\displaystyle{ ge_{M | m} = ga_{M | m} \left( \frac{1}{N} \sum_{i=1}^{N} gc_{m_i \to M} \right) }[/math]
其中,[math]\displaystyle{ ge_{M|m} }[/math] 表示宏观变量 [math]\displaystyle{ M }[/math] 在微观变量 [math]\displaystyle{ m }[/math] 集合中的格兰杰涌现性。该度量捕捉了弱涌现性的三个基本直觉:它是名义涌现性的一个子集,涉及对底层过程的依赖,并且它涉及从底层过程中的自主性。公式中的 [math]\displaystyle{ N }[/math] 表示微观变量的数量,[math]\displaystyle{ gc_{m_i \to M} }[/math] 表示单个微观变量 [math]\displaystyle{ m_i }[/math] 对宏观变量 [math]\displaystyle{ M }[/math] 的格兰杰因果性。重要的是,[math]\displaystyle{ ge_{M|m} }[/math] 将为零,如果 [math]\displaystyle{ M }[/math] 独立于 [math]\displaystyle{ m }[/math] 或者 [math]\displaystyle{ M }[/math] 完全被 [math]\displaystyle{ m }[/math] 预测。
在什么情况下格兰杰涌现性可能会很高?如果有“隐藏”或“潜在”的影响,即回归中未表现出来的相关微观因果因素,宏观变量可能从一组微观变量中涌现。然而,即使所有微观因果因素都存在,格兰杰涌现性仍可能因为依赖于所用的预测算法而产生。可以认为,事实上,为了在实践中有用,格兰杰涌现性是必要的,因为在某些情况下,宏观变量对预测算法来说比微观变量的集合更具有认识透明性。这也与Bedau的弱涌现性一致,在这种情况下,“除了通过模拟外不可导出”被格兰杰因果关系的“(不)可预测性”所取代。
非线性格兰杰涌现测量
对使用线性建模测量格兰杰涌现的一个明显批评是,一个宏观变量可能由于其是微观层面组件的非线性函数而表现为格兰杰涌现。因此,一个令人满意的涌现性度量不应依赖于线性方法未能检测到的非线性依赖性。幸运的是,扩展格兰杰因果关系(从而扩展格兰杰自主性和格兰杰涌现)到非线性情况是容易的,例如通过泰勒展开:
[math]\displaystyle{ X_1(t) = \sum_{k=1}^{q} \sum_{j=1}^{p} A_{11,j,k} X_1^k(t-j) +
\sum_{k=1}^{q} \sum_{j=1}^{p} A_{12,j,k} X_2^k(t-j) +
\sum_{k=1}^{q} \sum_{j=1}^{p} A_{13,j,k} X_3^k(t-j) + \xi_1(t) }[/math](1)
[math]\displaystyle{ X_2(t) = \sum_{k=1}^{q} \sum_{j=1}^{p} A_{21,j,k} X_1^k(t-j) + \sum_{k=1}^{q} \sum_{j=1}^{p} A_{22,j,k} X_2^k(t-j) + \sum_{k=1}^{q} \sum_{j=1}^{p} A_{23,j,k} X_3^k(t-j) + \xi_2(t) }[/math](2)
[math]\displaystyle{ X_3(t) = \sum_{k=1}^{q} \sum_{j=1}^{p} A_{31,j,k} X_1^k(t-j) + \sum_{k=1}^{q} \sum_{j=1}^{p} A_{32,j,k} X_2^k(t-j) + \sum_{k=1}^{q} \sum_{j=1}^{p} A_{33,j,k} X_3^k(t-j) + \xi_3(t) }[/math](3)
其中,[math]\displaystyle{ q }[/math]是泰勒展开中包含的多项式项数;请注意,变量集已经扩展为三个,以说明扩展到多变量([math]\displaystyle{ n\gt 2 }[/math])的情况。
在这个例子中:
[math]\displaystyle{ ge_{X_1 | X_2, X_3} = \log \left( \frac{\mathrm{var}(\xi_{1R(11)})}{\mathrm{var}(\xi_{1U})} \right) \times \frac{1}{2} \left( \log \left( \frac{\mathrm{var}(\xi_{1R(12)})}{\mathrm{var}(\xi_{1U})} \right) + \log \left( \frac{\mathrm{var}(\xi_{1R(13)})}{\mathrm{var}(\xi_{1U})} \right) \right) }[/math](4)
其中,根据之前的约定, [math]\displaystyle{ \xi_{1R(11)} }[/math]是从省略了[math]\displaystyle{ A_{ab} }[/math]系数的模型中得出的(如公式 (3))。如果相应的格兰杰自主性和格兰杰因果关系测量值本身在统计上显著,则线性或非线性格兰杰涌现性值可以被视为具有统计显著性。这可以通过对零假设进行F检验来评估,即[math]\displaystyle{ A_{11} }[/math](格兰杰自主性)和[math]\displaystyle{ A_{12} }[/math]...[math]\displaystyle{ A_{n} }[/math](格兰杰因果关系)的系数为零[9][16]。
值得注意的是,格兰杰涌现性的概念并不依赖于使用特定的非线性回归方法。还有其他更为复杂的方法比泰勒展开更不易受噪声观测的影响,并且涉及更少的参数。例如,Ancona等人[17]已经表明,径向基函数可以作为有效的回归核来测量非线性格兰杰因果关系。然而,出于当前的目的,泰勒方法是更可取的,因为(i)它简单易于描述和实施;(ii)统计显著性可以很容易地评估;(iii)它提供了格兰杰涌现性的明确公式(如公式 (4))。最后,注意格兰杰涌现性的值将取决于包含在 中的微观变量集。因此,在异质系统中,可以通过识别一个格兰杰涌现集,即能够最大化 的微观变量集。
格兰杰涌现方法的应用示例
鸟群模拟
现在,我将展示在一个简单的计算模型中,格兰杰涌现性如何表现出适当的行为。如前所述,一个经典的属性涌现示例是鸟群中的群集行为。在人工生命的开创性工作中,Reynolds[18]表明,通过为模拟的鸟(boids)组合三个简单规则,可以模拟出视觉上引人注目的鸟群集行为:
• 聚集:每只鸟倾向于飞向感知到的鸟群的质心(CM)。
• 规避:每只鸟倾向于避免与其他附近的boid碰撞。
• 协同:每只鸟倾向于将自己的速度与其他附近鸟的速度对齐。
这里使用一个简单的boid模拟来测试视觉上引人注目的群集行为是否与鸟群质心(宏观变量)相对于各个boid轨迹(微观变量)的高格兰杰涌现性相关。
模拟了个boid,在边长为200的环形方形环境中进行(所有维度和距离以任意单位表示;速度以每时间步为单位)。boid的初始位置和速度随机选取自范围 [0,200](位置),[0, 2π](航向),和 [3,9](速度)。在每个时间步中,每个boid的航向和速度 同步更新,更新规则如下:
[math]\displaystyle{ \alpha_i = \alpha_i + a_1\theta_1 + a_2(\pi + \theta_2) + a_3\theta_3 + r_1, }[/math] [math]\displaystyle{ s_i = s_i + a_4d\bar{s} + r_2, }[/math]
其中,[math]\displaystyle{ \alpha_i }[/math]表示第[math]\displaystyle{ i }[/math]的方向角。[math]\displaystyle{ \alpha_1,\alpha_2,\alpha_3 }[/math]是用于调整不同方向影响权重的参数(权重系数)。[math]\displaystyle{ \theta_1 }[/math]是朝向感知到的质心的方向(不包括boid [math]\displaystyle{ i }[/math] 的质心),[math]\displaystyle{ \theta_2 }[/math]是朝向最近boid的方向,[math]\displaystyle{ \theta_3 }[/math]是朝向所有其他boid的平均航向(在20单位范围内),[math]\displaystyle{ s_i }[/math]表示第[math]\displaystyle{ i }[/math]个boid的速度,[math]\displaystyle{ a_4 }[/math] 是用于调整速度变化的比例系数,决定了[math]\displaystyle{ d\bar{s} }[/math]对速度更新的影响程度,[math]\displaystyle{ d\bar{s} }[/math]是 boid [math]\displaystyle{ i }[/math] 的速度与20单位范围内其他boid的平均速度的差异,[math]\displaystyle{ r₁ }[/math]和 [math]\displaystyle{ r₂ }[/math]是范围 [-0.01, 0.01] 内的随机数。参数向量 [math]\displaystyle{ α }[/math](所有 [math]\displaystyle{ α }[/math] ∈ [0,1])决定了每个因素的相对贡献。环形距离按照标准方式计算,既可以跨越边界也可以不跨越边界。质心位置通过迭代计算以最小化每个boid与其他boid的环形距离(即不是与质心的平均距离,从而避免边界伪影)。
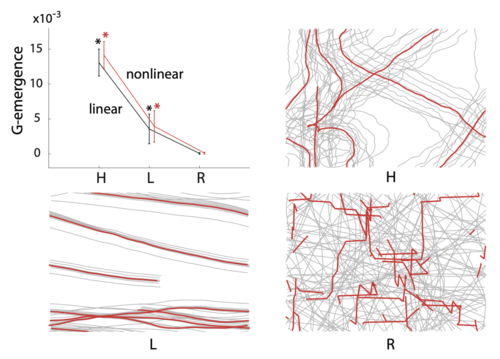
这里测试了三种不同的条件。条件[math]\displaystyle{ R }[/math](随机)产生了接近随机的boid行为[math]\displaystyle{ \alpha_R = \begin{bmatrix} 0.01 , 0.01 ,0.01 ,0.01 ,0.01 ,0.01 \end{bmatrix} }[/math]。条件[math]\displaystyle{ L }[/math](低)通过增强对速度匹配的强依赖性引发了较差的群集行为;在这种条件下的 boid 趋向于半刚性的队形移动[math]\displaystyle{ \alpha_L = \begin{bmatrix} 0.1 , 0.1 , 0.6 , 0.6 \end{bmatrix} }[/math]。条件[math]\displaystyle{ H }[/math](高)引发了引人注目的群集行为;参数集[math]\displaystyle{ \alpha_H = \begin{bmatrix} 0.1 , 0.3 , 0.3 , 0.3 \end{bmatrix} }[/math]是手动选择的。每种条件下 boid 和质心轨迹的示例显示在下图中,左上图为不同条件下线性和非线性格兰杰涌现性的均值和标准差(星号表示统计显著性),其它图为在条件[math]\displaystyle{ H }[/math](高格兰杰涌现性)、[math]\displaystyle{ L }[/math](低格兰杰涌现性)和[math]\displaystyle{ R }[/math](随机)下,boid(灰色)和CM(红色)的示例轨迹(500时间步片段)。尽管静态图像无法完全捕捉群集行为的动态特性,但很明显,条件[math]\displaystyle{ H }[/math] 下的 boid 轨迹比条件[math]\displaystyle{ L }[/math]和[math]\displaystyle{ R }[/math]下的更像群集行为。
鸟群涌现测量
对于每个条件,boid模拟运行了25次,每次运行持续5000个时间步;在每次运行中,记录了每个boid的x和y坐标以及全局质心。在计算格兰杰涌现性之前,进行了几个预处理步骤。为了降低数据集的维度,并增强对边界效应的鲁棒性,将每对x和y坐标转换为反映环境中心距离的单个变量。前500个数据点被移除,以消除初始瞬态效应,结果得到的时间序列被转换为零均值的等效时间序列。最后,为了确保协方差平稳性[19],对每个时间序列进行了一级差分处理。预处理完成后,在每个条件下的每次运行中,使用最小二乘回归分别计算了CM的线性和非线性格兰杰涌现性。我选择了模型阶数[math]\displaystyle{ p = 5 }[/math]和(用于非线性分析的)多项式阶数[math]\displaystyle{ q=3 }[/math]。模型阶数是基于所有75次运行的平均Akaike信息准则[13]选定的。
上图显示了每个条件下质心的平均线性和非线性格兰杰涌现性。结果证实了高格兰杰涌现性与引人注目的群集行为相关,线性和非线性度量均显示,条件[math]\displaystyle{ H }[/math]下的格兰杰涌现性显著高于条件[math]\displaystyle{ L }[/math]和[math]\displaystyle{ R }[/math]。条件[math]\displaystyle{ H }[/math]和[math]\displaystyle{ L }[/math]下的所有格兰杰涌现性值都是显著的(格兰杰自主性和格兰杰因果关系的[math]\displaystyle{ P }[/math]值均小于[math]\displaystyle{ 10^{-5} }[/math] ,双尾[math]\displaystyle{ t }[/math]检验);而条件[math]\displaystyle{ R }[/math]下的结果则不显著。
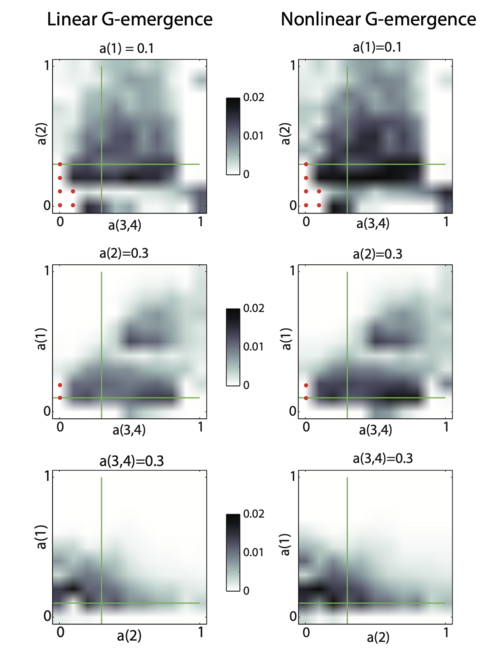
为了测试boid模型中不同参数组合下格兰杰涌现性的行为,我在参数空间[math]\displaystyle{ \alpha(1, 2, 3) \in [0.0, 0.1, \ldots, 1.0] }[/math] 中计算了每个参数向量的线性和非线性格兰杰涌现性。由于参数[math]\displaystyle{ \alpha_3 }[/math]和[math]\displaystyle{ \alpha_4 }[/math]都影响同一规则(速度匹配),它们被配对在一起进行评估,并为每个向量进行了三次评估,总共需要 [math]\displaystyle{ 11 \times 11 \times 11 \times 3 = 3993 }[/math]次评估。下图显示了穿过三维参数空间的三个正交剖面的格兰杰涌现性,在每个剖面中,向量[math]\displaystyle{ \alpha_{H} }[/math](条件[math]\displaystyle{ H }[/math])由绿色线的交点标记,灰度显示全局CM的平均线性和非线性格兰杰涌现性,每个值是5000时间步的三次评估的平均值,红点表示导致时间序列可靠地非平稳的参数组合。
这些剖面中有几个值得注意的方面。首先,线性和非线性格兰杰涌现性高度相关,这表明即使是线性度量在某些复杂系统中也能提供对涌现属性的洞见。其次,在参数空间的大多数区域中,格兰杰涌现性平滑变化,表明这是一种稳健的度量方法。然而,在某些区域中,出现了明显的跃迁,例如在一些[math]\displaystyle{ \alpha_1 = 0 }[/math] 的向量与其相邻向量之间的跃迁。格兰杰涌现性对这些跃迁的敏感性表明,它可以有效识别复杂模型中存在非平凡弱涌现的参数区域。
鸟群向下因果测量
一个关于涌现的普遍直觉是它涉及从宏观层面到微观层面的“向下”因果关系。对于强涌现的支持者来说,向下因果关系实际上是涌现本质的一个关键方面[2]。然而,向下因果关系的物理解释会引发复杂的形而上学问题,例如,如何解决微观和宏观因果之间的竞争[3]。格兰杰涌现性由于是统计定义的,提供了一种形而上学上无害的替代方案,其中向下因果关系反映为宏观变量对微观变量的格兰杰因果关系。
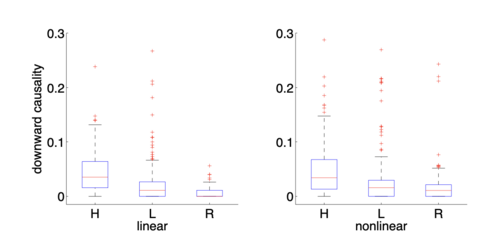
上图展示了从全局质心到boid个体轨迹的向下(格兰杰)因果关系,涵盖了线性和非线性的格兰杰因果关系测量。在每个条件下,对所有boid和所有25次运行取平均值。结果显示条件[math]\displaystyle{ H }[/math]下的向下因果关系显著高于条件[math]\displaystyle{ L }[/math]或[math]\displaystyle{ R }[/math]。箱线图显示了从全局CM到单个boid的线性和非线性格兰杰因果关系,分别计算了每个条件下所有25次运行中的每个boid(即每个箱线图包含250个值)。非显著的因果关系被设为零(名义阈值为0.01,经过Bonferroni校正为[math]\displaystyle{ 10^{-5} }[/math] )。所得分布为非正态分布,并使用Wilcoxon秩和检验比较各条件间的差异。对于线性和非线性分析,所有条件间的中位数成对比较差异均显著([math]\displaystyle{ p \lt 10^{-3} }[/math] )。每个箱线图显示下四分位数、中位数和上四分位数值;须线显示剩余数据的范围,‘[math]\displaystyle{ + }[/math]’号表示异常值。与涌现与向下因果关系之间的关联一致,向下因果关系的两种测量在条件[math]\displaystyle{ H }[/math]下明显高于条件[math]\displaystyle{ R }[/math]或[math]\displaystyle{ L }[/math]。尽管有这一结果,原则上弱涌现似乎可能在没有向下因果关系的情况下发生(当然,强涌现按定义需要向下因果关系)。拥有可分别应用的弱涌现和向下因果关系的测量方法,使得探索涌现和向下因果关系不同时发生的条件(如果存在)成为可能,从而潜在地细化和深化了涌现的概念。
格兰杰涌现方法的局限性
在本文中,我介绍了一种通过物理测量来检测系统中弱涌现程度的方法。由于该方法基于因果关系的统计解释,它规避了微观和宏观因果关系之间的竞争等概念上的难题,同时为微观到宏观推理路径的复杂性提供了客观且分级的评估方法。作者在个人网站上提供了用于计算G-涌现的 MATLAB 代码,适用于任意时间序列数据。
历时涌现问题
历时涌现(或称为时间涌现,Diachronic emergence)指的是随着时间推移,系统中出现新的属性,比如进化或发育过程中的变化。历时涌现的过程本质上是统计上不稳定的,因此不能直接用 G-涌现来测量。然而,我们可以假设历时涌现的过程由不同的、统计上稳定的时间段构成,而这些时间段有着不同的 G-涌现特性。通过这种方式,G-涌现可以间接推断出历时涌现的存在。
相变问题
近年来,物理学家开始对boid 模型中的自驱动粒子集体行为产生了兴趣[20][21]。在这些系统中,可以观察到从“气态”相(每个粒子独立运动)、“液态”相(粒子集体移动但相对彼此仍有扩散)、到“固态”相(粒子集体移动并彼此保持固定)等相变(Phase transitions)。这些相变可能分别对应于本文模型中的 [math]\displaystyle{ R }[/math]、[math]\displaystyle{ H }[/math] 和[math]\displaystyle{ L }[/math] 条件,穿过三维参数空间的三个正交剖面的格兰杰涌现性图中的边界可能代表了相变。不过,相变分析更侧重于转变的动态过程,并假定涌现行为在某些相中显而易见,而在其他相中不存在。相比之下,本文重点在于通过物理测量检测涌现程度。
与其他测量方法的关系
宏观预测
有学者[22]认为,预测能力的差异在定义宏观层次属性时可能至关重要。不过,他们的研究主要聚焦于澄清宏观状态的概念,而不是明确结合自主性和因果依赖的测量。相比之下,他们的预测效率测量是基于信息理论模型重构的,虽然很强大,但在实际应用中比本文提到的时间序列度量更复杂。类似的,Polani[23]提出的“涌现描述”还进一步涉及将系统分解为独立的信息子成分。
情境涌现
根据 Atmanspacher[24]提出的“情境涌现”(contextual emergence),推导宏观属性需要结合微观属性和特定情境条件(这些条件通过动力系统分析中的稳定性标准来定义)。这一概念不同于因果基础论,它表明微观属性只是推导宏观属性的必要但非充分条件,这暗示了强涌现的存在。
多尺度系统熵
Bar-Yam[25]提出了一种测量强涌现的方法,基于在多尺度上测量系统的熵。多尺度多样性的波动被认为揭示了不同变量值之间的约束,而这些约束在单独的变量中不存在,且被认为是强涌现的标志。然而,考虑到强涌现本质上拒绝机械解释,全面分析 Bar-Yam 的测量方法超出了本文的讨论范围。
在意识与强涌现领域的潜在应用
如前所述,强涌现与弱涌现有根本的不同,强涌现的属性被认为是无法从其微观成分中还原的,并且对这些微观成分产生向下的因果影响[26]。因此,强涌现给科学带来了极大的挑战,因为它暗示了世界上存在一些无法通过已知物理相互作用解释的真实属性。
David Chalmers 明确提出了一个反复出现的观点,即唯一一个明确的强涌现现象就是意识[6]。这种怀疑源自两个常见的直觉。首先,即使完全了解大脑中的物理互动,也不足以解释“有意识的体验是什么感觉”,这就是著名的“意识的难题”。其次,意识状态在世界上有因果作用的直觉,例如自由意志,这在意识的各个方面都有体现。毕竟,如果意识没有任何作用,那么为什么我们会有这些体验呢?这两个直觉恰好对应了强涌现的定义特征:宏观属性原则上无法从微观观察中辨别,且具有不可还原的因果力量。
然而,这些直觉可以被挑战。首先,期待科学解决“意识难题”可能是对科学解释自然角色的误解。科学理论并不需要复制它所解释的体验;就像飓风的理论并不是飓风本身一样[27])。如果体验的现象层面是不可还原的,这就像物理学无法解释为什么存在“某物而不是无物”(there is something rather than nothing)一样,但这并没有阻碍物理学家揭示许多其他的谜团。其次,意识可以在没有向下因果作用的情况下具有功能效用。完全有可能,某些神经机制支持的功能恰好伴随着意识体验[27]。例如,意识的神经机制可能在短时间内整合大量信息,从而在感觉运动场景中做出功能有效的高维度区分。这种信息整合可能必然带来意识的体验(qualia),正如血红蛋白的分子结构必然带来特定的光谱反应一样[21]。此外,“自由意志”和“意志”只是像其他体验一样的体验,且有大量实验证据表明,意识到某个自主行动之前,神经活动中已有可识别的信号[28]。总之,这些观点表明,意识与强涌现的联系并没有坚实的基础。
相比之下,神经机制与意识体验之间的联系很可能在许多方面涉及弱涌现。意识体验的一个显著特征是,它看起来像是某种“整体大于部分之和”的现象(每个意识体验都是一个整体),并且具有鲜明的时间流动感(William James 的“意识流”)。可以用弱涌现分析的意识模型因此有可能通过神经机制层面的动态过程来解释意识现象的特征。开发和实验测试这样的“解释关联”(explanatory correlates)[27]是科学描述意识的一个非常有前途的方向。考虑到弱涌现的测量方法最终可能用于解释自由意志,并帮助弥合神经机制与现象体验之间的解释鸿沟,这是令人兴奋的。
总结
理解现象的科学进展依赖于是否能够对其进行测量。到目前为止,“涌现”一直难以发展出有用的测量方法,可能是因为人们怀疑涌现必然违反机械或还原论的解释。然而,这种怀疑仅适用于强涌现,且强涌现的测量方法往往难以应用和解释[25]。在本文中,我提出并展示了一种量化、直观且实际可操作的弱涌现测量方法。G-涌现基于这样一种直观想法,即涌现属性既依赖于其组成部分,又具有一定的自主性[5],并通过线性和非线性时间序列分析进行了操作。
在鸟群飞行的模拟中,与随机运动或刚性队形飞行相比,视觉上引人注目的鸟群行为伴随着高 G-涌现。高 G-涌现还伴随着从鸟群整体到每只鸟的向下因果作用,尽管这种情况并非在所有系统中都存在。最后,G-涌现为测量其他类型的涌现提供了一个平台;例如,可以通过两个不同时期 G-涌现的变化来衡量时间涌现或自组织现象。
参考文献
- ↑ Broad C, ed. (1925). The mind and its place in nature. London: Routledge and Kegan Paul.
- ↑ 2.0 2.1 2.2 Kim J (1999). "Making sense of emergence". Philosophical Studies. 95 (3–36).
- ↑ 3.0 3.1 3.2 3.3 3.4 3.5 Bedau M (2003). "Downward causation and the autonomy of weak emergence". Principia. 6 (5–50).
- ↑ Chang H, ed. (2004). Inventing temperature: Measurement and scientific progress. New York, NY: Oxford University Press.
- ↑ 5.0 5.1 5.2 5.3 Bedau M (1997). "Weak emergence". Philosophical Perspectives. 11: 375–399.
- ↑ 6.0 6.1 6.2 Chalmers D (2006). The re-emergence of emergence. Oxford: Oxford University Press.
- ↑ Jackson F; Pettit P (1992). "In defence of explanatory ecumenism". Economics and Philosophy. 8 (1–21).
- ↑ Sperry R (1969). "A modified concept of consciousness". Psychological Review. 76 (532–536).
- ↑ 9.0 9.1 9.2 Granger C (1969). "Investigating causal relations by econometric models and cross-spectral methods". Econometrica. 37: 424–438.
- ↑ 10.0 10.1 Seth A (2007). "Granger causality". Scholarpedia. 2 (7): 1667.
- ↑ Ding M; Chen Y; Bressler S (2006). Granger causality: Basic theory and application to neuroscience. Wienheim: Wiley. p. 438–460.
- ↑ Seth A (2008). "Causal networks in simulated neural systems". Cognitive Neurodynamics. 2 (49–64).
- ↑ 13.0 13.1 13.2 Seth A (2007). Almeida e Costa F (ed.). Measuring autonomy via multivariate autoregressive modelling. Proceedings of the Ninth European Conference on Artificial Life. Springer-Verlag. p. 475–485.
- ↑ Varela F (1979). Principles of biological autonomy. North Holland, NY: Elsevier.
- ↑ Bertschinger N; Olbrich E; Ay N; Jost J (2008). "Autonomy: an information theoretic perspective". Biosystems.
- ↑ Geweke J (1982). "Measurement of linear dependence and feedback between multiple time series". Journal of the American Statistical Association. 77 (304–13).
- ↑ Ancona N; Marinazzo D; Stramaglia S (2004). "Radial basis function approaches to nonlinear granger causality of time series". Physical Review E. 70 (056221).
- ↑ Reynolds C (1987). Flocks, herds, and schools: A distributed behavioral model. Computer Graphics. Vol. 21. p. 25–34.
- ↑ Seth A (2005). "Causal connectivity of evolved neural networks during behavior". Network: Computation in Neural Systems. 16 (35–54).
- ↑ Vicsek T; Czirok A; Ben-Jacob E; Cohen I; Shochet O (1995). "Novel type of phase transition in a system of self-driven particles". Physical Review Letters. 75 (1226).
- ↑ 21.0 21.1 Edelman G (2003). "Naturalizing consciousness: A theoretical framework". Proceedings of the National Academy of Sciences, USA. 100 (9): 5520–5524.
- ↑ Shalizi C; Moore C (2006). "What is a macrostate: Subjective observations and objective dynamics".
{{cite journal}}: Cite journal requires|journal=(help) - ↑ Polani D (2006). "Emergence, intrinsic structure of information, and agenthood". Interjournal Complex Systems: 1973.
- ↑ Atmanspacher H (2007). "Contextual emergence from physics to cognitive neuroscience". Journal of consciousness studies. 14 (18–36).
- ↑ 25.0 25.1 Bar-Yam Y (2004). "A mathematical theory of strong emergence using multiscale variety". Complexity. 9 (6): 15–24.
- ↑ Kim J (2006). "Emergence: core ideas and issues". Synthese. 151 (547–559).
- ↑ 27.0 27.1 27.2 Seth A; Edelman G (2008). Meyers R. ed. Consciousness and complexity. Springer Verlag.
- ↑ Libet B (1985). "Unconscious cerebral initiative and the role of conscious will in voluntary action". Behavioral and Brain Sciences. 8 (529–566).