讨论:基于有效信息的因果涌现理论
2016年,Erik Hoel团队针对多时空尺度的系统,提出新的因果效能度量指标[math]\phi ^{max}[/math][1]。
摘要
复杂系统内的因果相互作用可以在多种时空尺度上分析。例如,大脑可以在神经元、神经元群、脑区的空间尺度,也可以10-1000毫秒的时间尺度上分析。人们普遍认为,一旦微观(micro)尺度确定,宏观尺度(macro)也就确定,这是关系被称为随附性(supervenience)。通常来说,虽然宏观尺度的描述是十分便利的,但只有微观才是因果完备(causally complete)的,因为微观包含系统所有因果有关的细节,而宏观尺度不会包含额外的因果信息。然而,这种假设只有通过正确的因果度量方法才可以进行验证。本文中我们使用一种有效信息(effective information, EI)的方法,基于系统运作机制的有效性和状态空间的大小进行定义的:高EI说明,系统机制在很大程度上可以描述过去和未来可能的状态空间。通过在微观机制明确的简单系统中计算微观和宏观尺度的EI大小,我们发现在特定的因果架构下EI能在空间/时间的宏观尺度上取得峰值。当粗粒化后的宏观机制比底层微观机制更加有效的情况下(确定性更高,以及/或简并性更小),就会出现这个现象,在一定程度上战胜了更小的状态空间。所以,尽管宏观从微观中随附产生 (supervene),但它可以在因果上取代微观(supersede),从而导致真实的因果涌现——即是从微观到宏观尺度的分析过程中EI的增加。
引言
在科学界,人们通常认为,若能更详细地描述复杂系统的因果机制,就更能清楚理解系统的工作原理。有时,采用“宏观”尺度进行描述会更加方便,因为不是所有的“微观”状态的数据都可以获得,一个粗糙的模型就足以使用。然而,完整理解系统运作方式,以及精准预测它的行为,似乎需要微观尺度所有因果相互作用的信息。例如,大脑在宏观尺度上以脑区和通路,介观(meso)尺度通过局部的神经元群,如微柱(minicolumns)和它们的连接性,微观尺度通过神经元和它们的突触来描述(1)。为了达到理解大脑完整工作机制的目标,已有一些项目开始从微观尺度对大脑进行建模 (2)。
科学中常用的还原主义方法不仅在实践中取得了成功,也有强有力的理论依据支持。主要的证据来源于直觉,我们认为当系统在微观尺度的物理机制确定了,那么它宏观尺度的性质也是确定的——前文提到的“随附”关系。相应的,随附性通常也使人们认为,微观尺度已经完成了所有的因果工作,即微观尺度是因果完备(causally complete)的,这种观点否认了宏观尺度的任何因果贡献。若非如此,即支持存在“多重因果”(multiple causation)。这种“因果排斥”(causal exclusion)的论点通常被用于反对在物理因果关系之上存在精神因果关系的可能性(5),也可以被应用于所有随附现象发生的情形,包括学科间的等级体系(6)。
然而一部分人认为真正因果涌现是有可能发生的,生物群(7)到蚁群(8)、大脑(9)和人类社会(10)的行为都提供了支持的案例。然而,尚不清楚如何判别一个系统是发生了真正的因果涌现,还是所有因果可以被还原到微观成分进行解释。目前大多数支持涌现的观点都是定性的(11)。一个令人信服的涌现实例必须证明,宏观尺度的因果描述可以胜过微观尺度[即因果涌现]。到目前为止,为数不多定量描述涌现的尝试都不是基于因果模型进行的(12)。
本文中,我们利用简单的模拟系统,包括类神经系统,定量地展现宏观尺度可以在因果上取代微观尺度,即因果涌现可以发生。我们通过扰乱每个系统的所有可能的因果状态库(“反事实”),并使用“有效信息”(EI)评估扰动的效果 (13)。EI是因果相互作用的一般性度量,因为它使用扰动(perturbation)来得到状态空间大小相关系统机制的有效性或选择性。正如下文将要指出的,EI对于确定性高且简并性低的系统是最大的,随着噪声(导致因果发散, causal divergence)和/或简并 (导致因果收敛, causal convergence)而减小。
对于每个系统,我们完整地描述了其微观尺度因果机制,因此任何宏观尺度上可能发生的事情都是确定的(随附性)。宏观尺度是通过在空间和/或时间维度对微观元素进行粗粒化(coarse graining)来定义的,这种映射定义了每个尺度上所有可能的因果组合。通过比较不同粗粒化尺度的EI,我们发现,根据系统的组织方式,因果相互作用可以在宏观而非微观时空尺度上达到峰值。因此,宏观是可能在因果关系上优于微观的,即便它产生于微观。评估系统粗粒化或细粒化引起的EI变化提供了一种量化因果涌现和因果退化的直接方法。
理论
在接下来的内容中,我们考虑一些相互连接的二值微元素构成的离散系统S,该系统的逻辑函数(机制)作用于其输入上。在描述状态独立 (state-independent)的EI之前,我们首先介绍一种状态依赖(state-dependent)的因果度量方法,即单个系统状态[math]S_0[/math]的“原因信息”和“结果信息”。
状态依赖的因果分析
[math]S[/math]的微观机制规定了其在微观时间步[math]t[/math]上的状态之间的转移概率矩阵(TPM)。基于Judea Pearl的因果分析扰动框架 (14,18),TPM可以在[math]t_0[/math]时刻(13)将[math]S[/math]扰动为以等概率[math](1/n)[/math]处于可能的[math]n[/math]个初始状态得到[math]\left[ do(S = s_i) \ \forall i \in 1 \dots n \right][/math],对应得到可能原因的无约束库[math]U^C[/math] (概率分布),这种扰动的方法使得[math]S0[/math]以最大熵分布,公平的概率分布可以避免外生状态集对因果模型的影响,打破与其他观测历史的关系,从而分离出对系统单纯的因果影响。原因分布决定了在[math]t+1[/math]时刻各结果状态的概率,对应于可能结果的无约束库[math]U^E[/math]。虽然[math]U^C[/math]等同于均匀分布,但是[math]U^E[/math]通常不是均匀分布的。系统当前状态[math]S = s_0[/math]与可能导致该状态的过去状态概率分布(通过贝叶斯规则获得的“原因库[math]S_P \mid s_0[/math]”),以及可能成为其结果的未来状态概率分布(“结果库[math]S_F \mid s_0[/math]”)相关联。因此,系统的机制和当前状态同时限制了可能的原因库UC和结果库UE。一种系统中因果相互作用的信息度量(15)方式因此可以被定义为有约束和无约束分布之间的差异[这里是[math]Kullback - Leibler[/math]散度([math]D_{KL}[/math]) (16)]:
[math]\displaystyle{ \text{Cause information}(s_0) = D_{KL}\left( \left( S_P \mid s_0 \right), U^C \right) }[/math]
[math]\displaystyle{ \text{Effect information}(s_0) = D_{KL}\left( \left( S_F \mid s_0 \right), U^E \right) }[/math]
因/果信息依赖于两个属性:(i)系统状态空间的大小(可能状态的集合),因为两种信息的上界都是都[math]log_2(n)[/math],;(ii) 系统机制在确定过去和未来状态方面的有效性。为了使有效性不受状态空间大小的影响,我们定义了以下归一化系数:
[math]\displaystyle{ \text{Cause coefficient}(s_0) = \frac{\text{Cause Information}(s_0)}{\log_2(n)} }[/math]
[math]\displaystyle{ \text{Effect coefficient}(s_0) = \frac{\text{Effect Information}(s_0)}{\log_2(n)} }[/math]
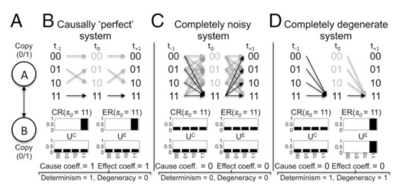
“原因系数(cause coefficient)”描述了一种状态在多大程度上可以充分确定其过去状态,而“结果系数(effect coefficient)”表明了一种状态确定其未来的结果状态的必要性(图1B)。结果系数本身是“确定性”和“简并性”两项的组合函数:
[math]\displaystyle{ \begin{aligned} \text{Effect coefficient}(s_0) &= \text{Determinism coefficient}(s_0) - \text{Degeneracy coefficient}(s_0) \\ &= \frac{1}{\log_2(n)} \sum_{s_F \in U^E} p(s_F \mid s_0) \log_2 \left( n \cdot p(s_F \mid s_0) \right) - \frac{1}{\log_2(n)} \sum_{s_F \in U^E} p(s_F \mid s_0) \log_2 \left( n \cdot p(s_F) \right) \end{aligned} }[/math]
确定性系数是系统状态的结果库和均匀分布(U)之间的差异[math]D_{KL}((S_F \mid s_0), U)[/math],除以[math]log_2(n)[/math],衡量的是根据[math]S_0[/math]确定系统未来状态的确定性(可靠)程度:当前状态完全导向未来单一状态概率时,该系数为1(完全确定性);当同等地导向未来每个状态时(即[math]p = 1/n[/math]),该系数为0(完全不确定性或噪声)。简并性系数度量从其他状态收敛由S0指定的未来状态的确定性程度(非噪声引起)。广义上,简并是指多条确定性路径导向了同一个结果或功能 (17,18)。当[math]S_0[/math]为任意状态都导向了同一个未来状态时,简并性系数为1(完全简并);而每个[math]S_0[/math]状态都导向不同的未来状态时,简并性系数为0(无简并性)。 在完全噪声或者完全退化(简并)的系统中,原因系数和结果系数都是最小的(0)(图1 C, D),在确定性和非退化(简并)的系统中系数达到最大(1)。单一状态对系统确定性和简并性的贡献最好通过分解结果系数得到。虽然原因系数也反映了系统的简并性和确定性,但在此不作进一步细分。
状态独立的因果分析
一个状态独立的系统因果度量方法可以通过在所有系统状态上取原因或结果信息的期望值来获得,这个量称为有效信息(EI):
[math]\displaystyle{ \begin{aligned} \ EI(S) &= \langle \text{Cause Information}(s_0) \rangle = \sum_{s_0 \in U^E} p(s_0) D_{KL} \left( (S_P \mid s_0), U^C \right)\\ &= \langle \text{Effect Information}(s_0) \rangle = \frac{1}{n} \sum_{s_0 \in U^C} D_{KL} \left( (S_F \mid s_0), U^E \right). \ \end{aligned} }[/math]
这两个计算式等价,因为当前假设为为时不变系统(time invariant, [math]\langle t_{-1} \rightarrow t_0\rangle = \langle t_0 \leftarrow t_{+1} \rangle[/math]),原因信息和结果信息通过贝叶斯公式关联。[math]EI[/math]也是所有可能原因和结果之间的互信息([math]mutual information, MI[/math]), [math]MI(U^C;U^E)[/math]。
作为一种因果度量方法,EI度量了系统中由因导向果的有效性(确定性和独特性),以及从果寻因的选择性。和状态依赖的方法一样,系统内因果相互作用的有效性([math]Eff[/math])也由用EI进行系统状态大小归一化后得到:[math]{Eff}(S) = \frac{{EI}(S)}{\log_2(n)}[/math],Eff也可以被分解为确定性和简并性两部分:
[math]\displaystyle{ \begin{aligned} \ Eff(S) &= \langle \text{Determinism coefficient}(s_0) \rangle - \langle \text{Degeneracy coefficient}(s_0) \rangle \\ &= \frac{\langle D_{KL}((S_F \mid s_0), U) \rangle}{\log_2(n)} - \frac{D_{KL}(U^E \mid U)}{\log_2(n)}. \ \end{aligned} }[/math]
因此,对于给定的系统规模,EI的最大值对应[math]{Eff}(S) = 1[/math],并且随着不确定性(由噪声引起的分散)或简并性(确定性收敛)而减小,对于完全噪声或简并性系统,[math]{Eff}(S) = 0[/math](图1c和D)。在具有最大有效性的系统中(图1B),每个原因都有一个唯一的结果,每个结果都有一个唯一的原因。因此,这样一个系统[math]{Eff}(S) = 1[/math]是完全可回溯/可预测的,从TPM中不仅可以推导出所有状态的唯一的未来轨迹,也可以推导出所有状态的唯一的过去轨迹(完全因果可逆性)。
分析的尺度
一个有限的离散系统[math]S[/math]可以在不同的尺度上考虑,从最细粒度的微观因果模型[math]S_m[/math]到各种粗粒度因果模型[math]S_M[/math]。假设所有宏观尺度[math]S_M都[/math]随附于微观尺度[math]S_m[/math]:给定[math]S_m[/math]的微观元素以及它们之间的因果关系,系统[math]S[/math]的所有可能因果模型的集合[math]\{S\}[/math]中的所有其他模型也都是确定的(19)。尽管[math]S_m[/math]可以确定[math]S_M[/math],但任何[math]S_M[/math]都可能被许多不同的较低尺度的描述所确定,这种特性被称为“多重可实现性”(20)。
特定尺度的扰动
微观尺度[math]S_m[/math]的因果分析需要将[math]S[/math]等概率地设置为所有可能的微观状态(即测试所有微观可能状态),然后决定结果效应。当对宏观尺度[math]S_M[/math]进行分析,[math]S[/math]也需要类似地以相同的概率设置为所有可能的宏观状态(即测试所有宏观可能状态)。当对任何宏观尺度进行因果度量时,需要将[math]S[/math]设置为所有[math]n_{micro}[/math]个微观状态[math]{S_m}[/math],分组进入相应的宏观状态[math]S_M[/math],对效应进行平均。以上通过进行“宏观扰动” 实现:
[math]\displaystyle{ do(S_M = s_M) = \frac{1}{n_{micro}} \sum_{s_{m,i} \in S_M} do(S_m = s_{m,i}) }[/math]
通过使用宏观扰动的办法,我们可以得到将[math]S_m[/math]进行任意尺度粗粒化后的因/果信息和[math]EI[/math]。宏观尺度的[math]EI[/math]等价于宏观因果集之间的[math]MI[/math]。
因果涌现/退化
最后,通过评估不同尺度粗粒化后的[math]{EI}(S)[/math],我们可以提问[math]{S}[/math]的因果尺度在哪个粗粒度达到最大值。这提供了因果涌现的一种分析定义,用比特表示:[math]CE = EI(S_M) – EI(S_m)[/math]。 因此,如果在宏观尺度上[math]EI(S_M)[/math]最大,而非微观尺度[math]S_m[/math],则[math]CE > 0[/math],说明发生了因果涌现。但如果在每个宏观尺度下都有[math]CE < 0[/math],则该系统有因果退化的属性。虽然这里的重点是相对于微观尺度[math]S_m[/math]的涌现/退化,但上述方法依然可用于比较不同宏观尺度下的因果性。
如上所述,[math]EI(S)[/math]既取决于系统状态库的大小,也取决于其机制的有效性。当从一个系统尺度到另一个尺度时,这两项都随着状态空间变化而变化,并且单个状态相对于过去的选择性,以及相对于未来的确定或简并性也随之变化。状态库大小和机制有效性对于[math]\Delta EI(S)[/math]的相对信息贡献可以用以下式子表示:
[math]\displaystyle{ \Delta I_{Eff} = ( {Eff}(S_M) - {Eff}(S_m) ) \cdot \log_2(n_M) }[/math]
[math]\displaystyle{ \Delta I_{Size} = {Eff}(S_m) \cdot ( \log_2(n_M) - \log_2(n_m) ) }[/math]
其中[math]n_{m/M}[/math]是[math]S_{m/M}[/math]的状态空间大小。以上式子满足[math]\displaystyle{ \Delta EI = \Delta I_{Eff} + \Delta I_{Size} = CE }[/math]。 正[math]\Delta I_{Eff}[/math]是由于宏观减少了微观尺度的简并性,或增加微观尺度的确定性,也可以由两者同时发生导致。值得注意的是,对微观尺度[math]S_m[/math]进行粗粒化为[math]S_M[/math]过程中导致[math]\Delta I_{Size}[/math]总是负数。所以,因果涌现出现就要求[math]\Delta I_{Eff}[/math]的增加量要超过[math]\Delta I_{Size}[/math]的减少。
讨论
本文提供了一种用于评估系统内因果相互作用在何种空间-时间粒度下达到最大的原则性方法。因果相互作用通过有效信息来评估,这一度量标准对系统机制的有效性和其状态空间的大小都敏感。通过模拟系统的例子表明,经过对空间和时间中的微观机制进行粗粒化处理后,EI在宏观尺度可能高于微观尺度。在这些情况下,可以说是宏观机制而不是微观机制在系统中进行了因果作用。
有效信息、有效性与涌现
在这里,EI是指系统机制的“有效性”,与状态集大小的乘积(用bits表示)。Eff(S)是所有系统状态中有效系数的平均值。有效系数衡量当前系统状态指定系统未来状态的必要性程度,是确定性减去简并性的函数。在原因端,与有效系数等价的是原因系数,它衡量由当前状态确定系统过去状态的充分性程度。对于某一个当前状态,原因和效应系数可能有所不同;例如,一种状态可能有多个原因但只有一个结果。然而,系统状态的有效系数的平均值,即有效性,对应于原因系数的平均值(按结果的概率加权)。换句话说,在一个时不变系统中,原因的平均选择性对应于结果的平均选择性。原则上,像EI这样的因果度量反映因果结构(选择性、确定性、简并性)和系统尺度的同时,也应该可以体现因果涌现。
通过模拟我们得到的主要结论是,通过在空间和时间上进行粗粒化处理,可以得到更高的EI值。尽管从定义上来说,微观尺度拥有比宏观尺度更大的状态空间集——这是微观尺度在EI上的一个优势。由于微观的固有优势,所以科学研究中一直默认使用还原论的方法(Causal reduction)。然而,上述例子表明,由于宏观尺度库容量减小导致的EI固有损失可以通过获得更高的有效性来补偿。换句话说,由微观机制所构建的宏观机制有更高的有效性,体现着宏观尺度的决定性增加或简并性减少。因此,只要在最优宏观尺度上存在EI增益(CE > 0),就可以说发生了真正的因果涌现。相反,如果存在EI损失(CE < 0),则系统属性为因果退化,微观尺度仍是因果分析的最佳尺度。本文采用的因果度量方法表明,定性或非因果度量等方式可能无法描述宏观尺度如何以及为什么比微观尺度具有更大的因果效应(22,23)。
微观-宏观映射和库容量
本文提供的方法可以公平地比较微观和宏观尺度的因果性。首先,模拟案例中宏观严格随附微观产生:一旦微观细节确定,所有的宏观尺度的表现也固定。特别是,宏观尺度没有额外的因果加入,例如一些只能应用于宏观的规则(24)。此外,从微观到宏观元素的映射过程中,微观元素本身的特征丢失;否则,宏观尺度仍有机会得到微观的信息,这将抵消宏观损失的库容量。最后,在进行因果评估时,微观和宏观尺度都独立地施加了均匀分布。为了在宏观尺度施加均匀分布的扰动,必须通过平均映射到同一宏观状态的微观状态来修改潜在微观扰动的概率。修正后的微观扰动分布产生宏观扰动的均匀分布,使得EI对各尺度的因果结构敏感,最终随附产生的宏观EI超过微观EI。
涌现是一个系统的内在性质
EI对因果性进行了度量,因为它要求通过所有可能的方式对系统进行扰动,然后评估扰动对系统的影响。同时它也是一种信息度量,因为取值也依赖于可能状态库的大小。实际上,在当前方法中,因果性和信息二者是必然有联系的,因此组成了“有效信息”一词。最后,测量EI体现了一个系统的“固有”性质,即对系统本身而言所有可能的系统态的平均有效性/选择性。有效性/选择性可以在不同的时空颗粒度下进行评估,并且EI取得最大值的颗粒度也是系统的固有性质。最大EI的尺度也不影响研究者在其他宏观、微观等尺度上开展有价值的研究(例如,神经科学家在离子通道、单个神经元、局部场电位或者功能磁共振信号的尺度上研究大脑)。因果涌现提示我们的是,最大EI的尺度是描述、预测和逆退系统行为的最佳尺度。
信息论中有与寻找EI最大化的宏观尺度相类似的方法:信道容量同样作为一种固有属性,定义为遍历所有可能的输入分布,可以通过信道以一定速率传输的最大信息量(27)。和寻找因果涌现的最佳粗粒度尺度的过程类似,但也有一些不同之处。首先,EI是通过扰动系统本身进行评估,而不是通过信道(系统是它自身的输入和输出)。其次,可以考虑的微观状态概率分布必须符合微观到宏观尺度的恰当映射(或恰当时间间隔)。因果涌现与其他现存方法的联系可以未来工作的中探讨,例如马尔可夫过程的可逆性和状态合并(28),或epsilon机(29)。
因果排斥及其含义
本文中用到的因果分析既支持随附性(在宏观尺度没有额外的因果关系),也支持因果排斥[对于给定时间的给定系统,因果关系只能发生在一个尺度,否则因果关系将被重复计算(4)]。然而,因果分析也指出,根据系统的结构,EI确实可以在宏观尺度取到最大值。在这种情况下,因果排除颠覆了还原论的假设,出于避免重复计算的考虑,最佳的宏观因果必须排除微观因果。换言之,宏观机制必须可以被分解为构成它的微观机制(随附性);然而,如果涌现发生了,宏观的因果不能被还原到微观尺度,这种情况下宏观在因果上战胜了微观并取而代之(取代性)。尺度之间不可约性的概念(宏观能战胜微观吗?)由尺度内元素子集之间的不可约性补充(整体大于部分之和吗?(15,25)) 。从系统的角度,涌现(CE>0)意味着在最优宏观尺度上的因果“自定义”了——在该尺度上,因果相互作用更加聚焦(30),且可以进行干预。
真实系统的可用性
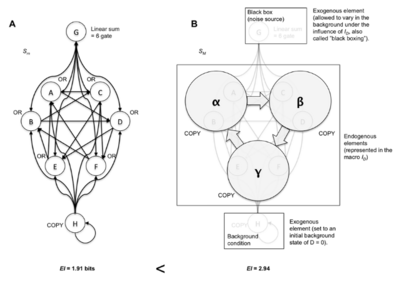
穷尽所有微观/宏观尺度EI的计算,对复杂的物理或生物系统而言是不可行的。然而,上述分析还是可以提供一些有价值的指导:(i)如果[math]Eff(S_m) >= Eff(S_M)[/math],因果涌现则不会发生,因果退化将保持;(ii)如果[math]EI(S_m) > log_2(n_M)[/math],其中nM是SM的状态库大小,那么因果退化依然保持; (iii) 在进行一些粗粒化后,Eff出现急剧增加,可以进一步关注是否产生因果涌现。所以,微观尺度已经接近最大有效性的系统表明因果退化。相比之下,具有自发活动,且能够区分出群体内/间联系的高度相连的元素群体,如图6所示的简化神经系统,更适合涌现发生。
在真实的神经系统中,人们可以在毫秒间隔内的单个神经元的微观尺度上,在数百毫秒间隔内的神经元群的介观尺度上,以及在几秒钟内的大脑区域的宏观尺度上(使用光遗传学和钙成像等工具)比较各自的有效信息。通过这种方式,一些经典的概念,如皮层微柱可能构成大脑功能的基本单位(31),或皮尺度对高试次间可变性(34)的工作时,通过群体(32)和速率方式(33)分别进行空间和时间编码,都可以使用有效性测量来严格检验。通过检验在复杂网络中被反复出现的小组团[例如大脑[35]],可以确定网络作为一个整体是倾向于涌现还是退化。对于涌现可能性的启发式评估也可以使用连接图图的分析,这可以提供退化的估计,再结合系统中固有噪声的数量的知识,可提供确定性的估计。
结论
本文研究的涌现方法为一个直观的想法提供了理论支持,即为了找出一个系统是如何工作的,人们应该找到会对系统本身“造成重要差异的差异部分”(25)(36)。它还表明,像大脑这样复杂的多尺度系统可能在宏观尺度上“工作”,因为在生物系统中,自然选择的加工过程必须处理一些不可预测性,进而导致生物系统的简并性(18)。需要处理噪声和简并的工程系统。该理论更进一步说明,从微观物理学到宏观经济学,科学的尺度结构可能不仅仅是为了便利,而且是在组织的相关尺度上因果收益最大的真实反映。
有效信息与香农熵的关系
过去,少数直接比较宏观和微观的涌现概念都隐含或明确地假设,宏观尺度最多只能是微观尺度的压缩(37-39)。这是可以理解的,因为任何宏观因果模型的特征都是其简化的状态空间。然而,压缩通常是有损的,至多达到无损。专注于压缩只能发现宏观尺度最多只能是微观尺度的压缩等效物。相比之下,在因果涌现理论中,占主导地位的概念是香农发现的信道容量,以及信息编码如何利用它实现可靠通信。 一个信道由两个有限集合X和Y,以及转移概率[math]p(Y \mid X)[/math]的集合组成,使得对于每个X和Y, [math]p(Y \mid X) ≥ 0[/math],对于每个X,[math]\sum_y p(Y \mid X) = 1[/math](被称为信道矩阵)。X和Y分别是信道的输入和输出(40)。信道矩阵作为一个固定实体控制信道。类似地,因果结构是由干预及其效果之间的关系所支配的,也是固定实体。值得注意的是,信通和因果结构都可以表示为TPMs,并且在信道矩阵包含与某些状态转换集相同的转换概率的情况下,TPMs将是相同的。因果结构是一个将过去状态转化为未来状态的矩阵。 互信息[math]I(X; Y)[/math]最初是由Claude Shannon提出的度量,用来捕获可以在信道上传输的信息的速率。互信息[math]I(X; Y)[/math]可以表示为:
[math]\displaystyle{ I(X; Y) = H(X) - H(X \mid Y) }[/math]
H(X)表示源的总可能熵,在因果分析中对应某组干预[math]I_D[/math],因此[math]H(X) = H(I_D)[/math]。条件熵[math]H(X \mid Y)[/math]捕获在考虑Y后关于X的剩余信息。因此,[math]H(X \mid Y)[/math]有一个明确的因果解释,即在一系列干预措施中丢失的信息量。更具体地说,它是由于缺乏有效性而丢失的信息。从已知条件熵公式[math]H(X \mid Y)= H(X) − I(X; Y)[/math],通过替换因果术语得到[math]H(I_D \mid E_D) = H(I_D)−I(I_D; E_D)[/math],我们可以得到[math]H(I_D \mid E_D) = H(I_D)−(H(I_D) \cdot eff)[/math]。再次通过转换[math]H(I_D \mid E_D) =(1 − eff) \cdot H(I_D)[/math]可证明,[math]H(I_D \mid E_D)[/math]确实捕获了缺乏的有效性。
[math]\displaystyle{ EI = I(I_D; E_D) = H(I_D) - H(I_D \mid E_D) = H(I_D) - ((1 - eff) \cdot H(I_D)) = eff \cdot H(I_D). }[/math]
因此,我们可以直接说明宏观如何战胜微观:虽然H(ID)在宏观尺度上必然减少,但条件熵[math]H(I_D \mid E_D)[/math]可能会更大程度地减少,从而使总互信息提高。
信道具有一定的容量,容量具体是指一个信道以最具信息量和最可靠的方式将输入转化为输出的能力。Shannon发现,信道上的信息传输速率对输入概率分布[math]p(X)[/math]的变化很敏感。信道([math]C[/math])的容量由使互信息最大化的输入集合来定义,这也是信道能够可靠传输信息的最大速率:
[math]\displaystyle{ C = \max_{p(X)} I(X; Y) }[/math]
因果涌现理论揭示了系统中存在类似的因果容量。因果容量([math]CC[/math])是一个系统以最大信息量和最有效的方式将干预转化为结果的能力:
[math]\displaystyle{ CC = \max_{(I_D)} (I_D; E_D). }[/math]
正如改变通道的输入概率[math]p(X)[/math]会增加[math]I(X; Y)[/math]一样,改变干预分布([math]I_D[/math])也会增加EI。宏观使用的干预改变或扭曲了[math]I_D[/math],导致因果涌现。相应地,拥有 [math]EI_{max}[/math]的宏观尺度因果模型(及其关联的[math]I_D[/math]和[math]E_D[/math])是最充分利用系统因果容量的模型。尽管[math]I_D[/math]有这种扭曲,但从某些宏观尺度来看,[math]I_D[/math]仍然处于[math]H_{max}[/math],因为每个[math]do(s_M)[/math]都是等概率的([math]E_D[/math]是一组宏观效应)。
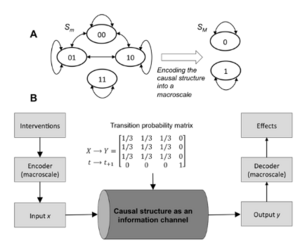
由此可见,系统的更高时空尺度是什么:一种因果结构的通道编码形式。宏观尺度是一种消除因果关系不确定性的编码,从而利用了更多可用的因果容量。图7使用输入X、输出Y(t, t+1)的TPM给出了这种因果编码的示例:
[math]\displaystyle{ I_D \to E_D = \begin{bmatrix} \frac{1}{3} & \frac{1}{3} & \frac{1}{3} & 0 \\ \frac{1}{3} & \frac{1}{3} & \frac{1}{3} & 0 \\ \frac{1}{3} & \frac{1}{3} & \frac{1}{3} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}. }[/math]
要通过具有以上属性的信道矩阵发送信息,需要定义一些编码/解码函数。信息可能是一些二进制字符串,例如,通过某个[math]I_D[/math]生成的{001011010011}。编码函数φ: {message}→{encoder}是一个规则,它将一些信道输入和一些输出,以及一些解码函数ψ联系起来。编码/解码函数一起创建了码本。
我们现在可以定义宏观与微观尺度的编码:微观尺度编码对应从φ : {x1, x2, x3, x4} → {00, 01, 10, 11} 的一一映射,解码函数:ψ : {00, 01, 10, 11}→ {y1, y2, y3, y4},每个微观状态 x 都携带其独特的信息。以这种方式干预系统的熵[math]H(I_D) = 2 bits[/math],因为它的四种可能状态是连续的随机干预(因此[math]p(1) = 0.5[/math])。每个码指定一个传输速率[math]R = n/t[/math],其中[math]t[/math]是系统的每次状态转换,[math]n[/math]是每次转换发送的比特数。上述系统的微观尺度编码速率[math]R = 2 bits[/math],但这2 bits发送并不可靠。这是因为[math]H(I_D \mid E_D)[/math]比较大:1.19 bits,所以[math]I(I_D; E_D) = H(I_D)−H(I_D \mid E_D) = 0.81 bits[/math]。在实际应用中,这意味着如果想要发送消息{00,10,11,01,00,11},这将需要使用6个通道,并且出现大量错误的可能性非常高。这是因为速率R超过了微观尺度的容量。
相反,我们可以将宏尺度编码函数定义为多对一映射Φ:{x1, x2, x3}→{0};{x4}→{1},类似Ψ:{y1, y2, y3}→{0};{y4}→{1},使得只有宏观状态被用作干预,即假设它们携带不同的信息。这套编码发送消息的速度慢了两倍,因为[math]R = 1 bit[/math],并且对应的熵[math]H(I_D)[/math]减半(1 bit;p(1) = 0.83)。因为[math]H(I_D \mid E_D) = 0,I(I_D; E_D) = 1 bit[/math],表明可靠的干预可以以1 bit的速率进行,比使用微观尺度编码的速率高。在这个宏观尺度上,传递任何信息都不会有错误,通信速率等于容量C。
因此可以说明因果涌现需要对称性破缺。当通道的行[math]p(y \mid x)[/math]和列互为排列时,信道被定义为对称的。如果行概率是彼此的排列,并且满足所有列和相等,则信道是弱对称的。对于任何这样的对称通道,产生[math]I_{max}[/math]的输入分布已被证明为均匀分布[math]H_{max}[/math]。在微观尺度上处理系统意味着[math]I_D = H_{max}[/math]。因此,对于对称或弱对称系统,微观尺度提供了最佳的因果模型,而无需在模型空间中搜索。只有在因果关系不对称的系统中,才可能出现因果涌现。
因果容量近似通道容量
使用系统所有因果容量的因果模型有一个有关联的[math]I_D[/math],它以与使用所有通道容量的输入分布方式相同:在通道使用期间仅发送可能消息的子集。然而,因果容量受到通道容量的限制,它们并不总是相同的。由于[math]I_D[/math]的扭曲是模型选择的函数,模型选择以各种方式(可能分布中的子集)受到约束,因此因果容量是更一般形式的信道容量(在所有可能分布上定义)的特殊情况。粗粒度是通过移动到宏观尺度来操纵(扭曲)[math]I_D[/math]的一种方法。这不是更改[math]I_D[/math](和关联[math]E_D[/math])的唯一方法。在对一个系统进行因果建模时所做的选择,包括选择创建因果模型的尺度,也包括选择初始条件,以及将变量分类为因果模型的外生或内生(“黑箱”),都是模型选择的形式,都可以扭曲ID和改变ED,导致因果出现。 例如,考虑一个由8个状态组成的马尔可夫链系统:
[math]\displaystyle{ S_m = \begin{bmatrix} 1/8 & 1/8 & 1/8 & 1/8 & 1/8 & 1/8 & 1/8 & 1/8 \\ 1/8 & 1/8 & 1/8 & 1/8 & 1/8 & 1/8 & 1/8 & 1/8 \\ 1/8 & 1/8 & 1/8 & 1/8 & 1/8 & 1/8 & 1/8 & 1/8 \\ 1/8 & 1/8 & 1/8 & 1/8 & 1/8 & 1/8 & 1/8 & 1/8 \\ 1/8 & 1/8 & 1/8 & 1/8 & 1/8 & 1/8 & 1/8 & 1/8 \\ 1/8 & 1/8 & 1/8 & 1/8 & 1/8 & 1/8 & 1/8 & 1/8 \\ 1/8 & 1/8 & 1/8 & 1/8 & 1/8 & 1/8 & 1/8 & 1/8 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{bmatrix} }[/math]
其中链中的一些状态在转换过程中是完全随机的。如果[math]I_D[/math]为[math]H_{max}[/math],则[math]EI = 0.63 bits[/math]。然而,每个因果模型都隐含地将变量分类为模型的内生或外生变量。例如,在这里,我们可以将最后两种状态(s7, s8)作为宏观因果模型的内生状态,而将其余状态作为外生状态。从状态空间减小的角度出发,这个限制带来的仍然是一个宏观模型。对于系统的宏观因果模型[math]EI = 1 bit[/math],意味着因果涌现发生,再次因为[math]I_D[/math]被模型选择扭曲。这种扭曲本身可以量化为干预分布[math]H(I_D)[/math]中的熵损失:
[math]\displaystyle{ \begin{aligned} I_D(\text{warped}) = \begin{bmatrix} 0 & 0 & 0 & 0 & 0 & 0 & 1/2 & 1/2 \end{bmatrix} \\ \uparrow \\ I_D = \begin{bmatrix} 1/8 & 1/8 & 1/8 & 1/8 & 1/8 & 1/8 & 1/8 & 1/8 \end{bmatrix} \end{aligned} }[/math]
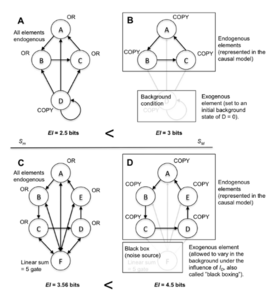
将带噪声或退化状态置为因果模型的外生状态可以导致因果涌现,所以这里可以设置一些外生元素。 值得注意的是,有多种方法可以将元素设置为外生(不显式地将它们包含在宏观模型中)。例如,外生因素通常是因果模型中隐含的背景假设。这样的背景条件可以包括为因果分析将外生元素设置为特定状态(冻结),或将系统设置为初始条件。或者,可以允许元素在应用的[math]I_D[/math]的影响下变化。后一种形式被称为“黑箱”,元素的内部工作或在系统中的作用是无法查看的(41,42)。在图8中,两种类型的模型选择显示在确定性互连逻辑门的系统中。每个模型选择都会导致因果涌现。
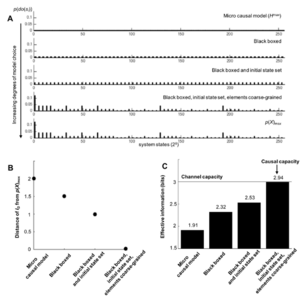
与其在因果模型的构建中精确地规定什么类型的模型选择是“允许的”,不如区分出一个更普遍的原则:通过模型构建选择扭曲[math]I_D[/math]的方法越多,因果容量就越接近实际通道容量。例如,考虑图9A中的系统。在图9B中,显示了一个宏观尺度,它使用各种类型的模型选择(通过粗粒度,黑盒元素,并为外生元素设置特定的初始条件)来演示因果涌现。如图10所示,模型选择的自由度越大,因果容量越接近通道容量。在模拟了数百万个随机概率分布p(X),寻找最大I的概率分布后,通过梯度上升找到了该系统的通道容量。模型选择使微观尺度[math]I_D[/math]向p(X)靠拢,如图10B所示。随着模型选择的增加,[math]EI_{max}[/math]接近信道容量的[math]I_{max}[/math] (图10C)。
- ↑ Hoel, E.P., Albantakis, L., Marshall, W. and Tononi, G. Can the macro beat the micro? Integrated information across spatiotemporal scales[J]. Neuroscience of Consciousness, 2016, 2016(1), p.niw012.