Causal Emergence
Causal emergence refers to a special kind of emergence phenomenon in dynamical systems, that is, the system will exhibit stronger causal characteristics on a macroscopic scale. In particular, for a class of Markov dynamical systems, after appropriate coarse-graining of its state space, the formed macroscopic dynamics will exhibit stronger causal characteristics than the microscopic ones. Then it is said that causal emergence occurs in this system [1][2]. At the same time, the causal emergence theory is also a theory that uses causal effect measures to quantify emergence phenomena in complex systems.
1. History
The causal emergence theory is a theory that attempts to answer the question of what emergence is from a phenomenological perspective using a causal-based quantitative research method. Therefore, the development of causal emergence is closely related to people's understanding and development of concepts such as emergence and causality.
Emergence
Emergence has always been an important characteristic in complex systems and a core concept in many discussions about system complexity and the relationship between the macroscopic and microscopic levels [3][4]. Emergence can be simply understood as the whole being greater than the sum of its parts, that is, the whole exhibits new characteristics that the individuals constituting it do not possess [5]. Although scholars have pointed out the existence of emergence phenomena in various fields [4][6], such as the collective behavior of birds [7], the formation of consciousness in the brain, and the emergent capabilities of large language models [8], there is currently no universally accepted unified understanding of this phenomenon. Previous research on emergence mostly stayed at the qualitative stage. For example, Bedau et al. [9][10] conducted classified research on emergence, dividing emergence into nominal emergence [11][12], weak emergence [9][13], and strong emergence [14][15].
Nominal emergence can be understood as attributes and patterns that can be possessed by the macroscopic level but not by the microscopic level. For example, the shape of a circle composed of several pixels is a kind of nominal emergence [11][12].
Weak emergence refers to the fact that macroscopic-level attributes or processes are generated by complex interactions between individual components. Or weak emergence can also be understood as a characteristic that can be simulated by a computer in principle. Due to the principle of computational irreducibility, even if weak emergence characteristics can be simulated, they still cannot be easily reduced to microscopic-level attributes. For weak emergence, the causes of its pattern generation may come from both microscopic and macroscopic levels [14][15]. Therefore, the causal relationship of emergence may coexist with microscopic causal relationships.
As for strong emergence, there are many controversies. It refers to macroscopic-level attributes that cannot be reduced to microscopic-level attributes in principle, including the interactions between individuals. In addition, Jochen Fromm further interprets strong emergence as the causal effect of downward causation [16]. Downward causation refers to the causal force from the macroscopic level to the microscopic level. However, there are many controversies about the concept of downward causation itself [17][18].
From these early studies, it can be seen that emergence has a natural and profound connection with causality.
Causality and its measurement
The so-called causality refers to the mutual influence between events. Causality is not equal to correlation, which is manifested in that not only will B occur when A occurs, but also if A does not occur, then B will not occur. Only by intervening in event A and then examining the result of B can people detect whether there is a causal relationship between A and B.
With the further development of causal science in recent years, people can use a mathematical framework to quantify causality. Causality describes the causal effect of a dynamical process [19][20][21]. Judea Pearl [21] uses probabilistic graphical models to describe causal interactions. Pearl uses different models to distinguish and quantify three levels of causality. Here we are more concerned with the second level in the causal ladder: intervening in the input distribution. In addition, due to the uncertainty and ambiguity behind the discovered causal relationships, measuring the degree of causal effect between two variables is another important issue. Many independent historical studies have addressed the issue of measuring causal relationships. These measurement methods include Hume's concept of constant connection [22] and value function-based methods [23], Eells and Suppes' probabilistic causal measures [24][25], and Judea Pearl's causal measure indicators, etc. [19].
Causal emergence
Emergence and causality are also interconnected: on the one hand, emergence is the causal effect of complex nonlinear interactions among the components of a complex system; on the other hand, emergent characteristics will also have causal relationships with individuals in complex systems. In addition, in the past, people were accustomed to attributing macroscopic factors to the influence of microscopic factors. However, macroscopic emergent patterns often cannot find microscopic attributions, so corresponding causes cannot be found. Thus, there is a profound connection between emergence and causality. On the other hand, although we have a qualitative classification of emergence, we cannot quantitatively characterize the occurrence of emergence. Therefore, we can use causality to quantitatively characterize the occurrence of emergence.
In 2013, Erik Hoel, an American theoretical neurobiologist, tried to introduce causality into the measurement of emergence, proposed the concept of causal emergence, and used effective information (EI for short) to quantify the strength of causality in system dynamics [1][2]. Causal emergence can be described as: when a system has a stronger causal effect on a macroscopic scale compared to its microscopic scale, causal emergence occurs. Causal emergence well characterizes the differences and connections between the macroscopic and microscopic states of a system. At the same time, it combines the two core concepts of causality in artificial intelligence and emergence in complex systems. Causal emergence also provides scholars with a quantitative perspective to answer a series of philosophical questions. For example, the top-down causal characteristics in life systems or social systems can be discussed with the help of the causal emergence framework. The top-down causation here refers to downward causation [26], indicating the existence of macroscopic-to-microscopic causal effects. For example, in the phenomenon of a gecko breaking its tail. When in danger, the gecko breaks its tail directly without asking for the tail's advice. Here, the whole is the cause and the tail is the effect. Then there is a causal force from the whole pointing to the part.
Early work on quantifying emergence
There have been some related works in the early stage that attempted to quantitatively analyze emergence. The computational mechanics theory proposed by Crutchfield et al. [27] considers causal states. This method discusses related concepts based on the division of state space and is very similar to Erik Hoel's causal emergence theory. On the other hand, Seth et al. proposed the G-emergence theory [28] to quantify emergence by using Granger causality.
Computational mechanics
The computational mechanics theory attempts to express the causal laws of emergence in a quantitative framework, that is, how to construct a coarse-grained causal model from a random process so that this model can generate the time series of the observed random process [27].
Here, the random process can be represented by [math]\displaystyle{ \overleftrightarrow{s} }[/math]. Based on time [math]\displaystyle{ t }[/math], the random process can be divided into two parts: the process before time [math]\displaystyle{ t }[/math] and the process after time [math]\displaystyle{ t }[/math], [math]\displaystyle{ \overleftarrow{s_t} }[/math] and [math]\displaystyle{ \overrightarrow{s_t} }[/math]. Computational mechanics records the set of all possible historical processes [math]\displaystyle{ \overleftarrow{s_t} }[/math] as [math]\displaystyle{ \overleftarrow{S} }[/math], and the set of all future processes as [math]\displaystyle{ \overrightarrow{S} }[/math].
The goal of computational mechanics is to establish a model that hopes to reconstruct and predict the observed random sequence in a certain degree of accuracy. However, the randomness of the sequence makes it impossible for us to obtain a perfect reconstruction. Therefore, we need a coarse-grained mapping to capture the ordered structure in the random sequence. This coarse-grained mapping can be characterized by a partitioning function [math]\displaystyle{ \eta: \overleftarrow{S}→\mathcal{R} }[/math], which can divide [math]\displaystyle{ \overleftarrow{S} }[/math] into several mutually exclusive subsets (all mutually exclusive subsets form the complete set), and the formed set is denoted as [math]\displaystyle{ \mathcal{R} }[/math].
Computational mechanics regards any subset [math]\displaystyle{ R \in \mathcal{R} }[/math] as a macroscopic state. For a set of macroscopic state sets [math]\displaystyle{ \mathcal{R} }[/math], computational mechanics uses Shannon entropy to define its statistical complexity index [math]\displaystyle{ C_\mu }[/math] to measure the complexity of the state. The following equation:
[math]\displaystyle{ C_\mu(\mathcal{R})\triangleq -\sum_{\rho\in \mathcal{R}} P(\mathcal{R}=\rho)\log_2 P(\mathcal{R}=\rho) }[/math]
It can be proved that when a set of states is used to build a prediction model, statistical complexity is approximately equivalent to the size of the prediction model.
Furthermore, in order to achieve the best balance between predictability and simplicity for the set of macroscopic states, computational mechanics defines the concept of causal equivalence. If [math]\displaystyle{ P\left ( \overrightarrow{s}|\overleftarrow{s}\right )=P\left ( \overrightarrow{s}|{\overleftarrow{s}}'\right ) }[/math], then [math]\displaystyle{ \overleftarrow{s} }[/math] and [math]\displaystyle{ {\overleftarrow{s}}' }[/math] are causally equivalent. This equivalence relation can divide all historical processes into equivalence classes and define them as causal states. All causal states of the historical process [math]\displaystyle{ \overleftarrow{s} }[/math] can be characterized by a mapping [math]\displaystyle{ \epsilon \left ( \overleftarrow{s} \right ) }[/math]. Here, [math]\displaystyle{ \epsilon: \overleftarrow{\mathcal{S}}\rightarrow 2^{\overleftarrow{\mathcal{S}}} }[/math] is a function that maps the historical process [math]\displaystyle{ \overleftarrow{s} }[/math] to the causal state [math]\displaystyle{ \epsilon(\overleftarrow{s})\in 2^{\overleftarrow{\mathcal{S}}} }[/math].
Further, we can denote the causal transition probability between two causal states [math]\displaystyle{ S_i }[/math] and [math]\displaystyle{ S_j }[/math] as [math]\displaystyle{ T_{ij}^{\left ( s \right )} }[/math], which is similar to a coarsened macroscopic dynamics. The [math]\displaystyle{ \epsilon }[/math]-machine of a random process is defined as an ordered pair [math]\displaystyle{ \left \{ \epsilon,T \right \} }[/math]. This is a pattern discovery machine that can achieve prediction by learning the [math]\displaystyle{ \epsilon }[/math] and [math]\displaystyle{ T }[/math] functions. This is equivalent to defining the so-called identification problem of emergent causality. Here, the [math]\displaystyle{ \epsilon }[/math]-machine is a machine that attempts to discover emergent causality in data.
Computational mechanics can prove that the causal states obtained through the [math]\displaystyle{ \epsilon }[/math]-machine have three important characteristics: "maximum predictability", "minimum statistical complexity", and "minimum randomness", and it is verified that it is optimal in a certain sense. In addition, the author introduces a hierarchical machine reconstruction algorithm that can calculate causal states and [math]\displaystyle{ \epsilon }[/math]-machines from observational data. Although this algorithm may not be applicable to all scenarios, the author takes chaotic dynamics, hidden Markov models, and cellular automata as examples and gives numerical calculation results and corresponding machine reconstruction paths.
Although the original computational mechanics does not give a clear definition and quantitative theory of emergence, some researchers later further advanced the development of this theory. Shalizi et al. discussed the relationship between computational mechanics and emergence in their work. If process [math]\displaystyle{ {\overleftarrow{s}}' }[/math] has higher prediction efficiency than process [math]\displaystyle{ \overleftarrow{s} }[/math], then emergence occurs in process [math]\displaystyle{ {\overleftarrow{s}}' }[/math]. The prediction efficiency [math]\displaystyle{ e }[/math] of a process is defined as the ratio of its excess entropy to its statistical complexity ([math]\displaystyle{ e=\frac{E}{C_{\mu}} }[/math]). [math]\displaystyle{ e }[/math] is a real number between 0 and 1. We can regard it as a part of the historical memory stored in the process. In two cases, [math]\displaystyle{ C_{\mu}=0 }[/math]. One is that this process is completely uniform and deterministic; the other is that it is independently and identically distributed. In both cases, there cannot be any interesting predictions, so we set [math]\displaystyle{ e=0 }[/math]. At the same time, the author explains that emergence can be understood as a dynamical process in which a pattern gains the ability to adapt to different environments.
The causal emergence framework has many similarities with computational mechanics. All historical processes [math]\displaystyle{ \overleftarrow{s} }[/math] can be regarded as microscopic states. All [math]\displaystyle{ R \in \mathcal{R} }[/math] correspond to macroscopic states. The function [math]\displaystyle{ \eta }[/math] can be understood as a possible coarse-graining function. The causal state [math]\displaystyle{ \epsilon \left ( \overleftarrow{s} \right ) }[/math] is a special state that can at least have the same predictive power as the microscopic state [math]\displaystyle{ \overleftarrow{s} }[/math]. Therefore, [math]\displaystyle{ \epsilon }[/math] can be understood as an effective coarse-graining strategy. Causal transfer [math]\displaystyle{ T }[/math] corresponds to effective macroscopic dynamics. The characteristic of minimum randomness characterizes the determinism of macroscopic dynamics and can be measured by effective information in causal emergence.
G-emergence
The G-emergence theory was proposed by Seth in 2008 and is one of the earliest studies to quantitatively quantify emergence from a causal perspective [28]. The basic idea is to use nonlinear Granger causality to quantify weak emergence in complex systems.
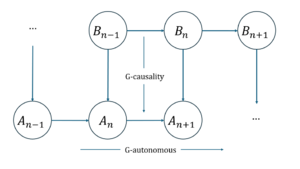
Specifically, if we use a binary autoregressive model for prediction, when there are only two variables A and B, there are two equations in the autoregressive model, each equation corresponds to one of the variables, and the current value of each variable is composed of its own value and the value of the other variable within a certain time lag range. In addition, the model also calculates residuals. Here, residuals can be understood as prediction errors and can be used to measure the degree of Granger causal effect (called G-causality) of each equation. The degree to which B is a Granger cause (G-cause) of A is calculated by taking the logarithm of the ratio of the two residual variances, one being the residual of A's autoregressive model when B is omitted, and the other being the residual of the full prediction model (including A and B). In addition, the author also defines the concept of G-autonomous, which represents a measure of the extent to which the past values of a time series can predict its own future values. The strength of this autonomous predictive causal effect can be characterized in a similar way to G-causality.
As shown in the above figure, we can judge the occurrence of emergence based on the two basic concepts in the above G-causality (here is the measure of emergence based on Granger causality, denoted as G-emergence). If A is understood as a macroscopic variable and B is understood as a microscopic variable. The conditions for emergence to occur include two: 1) A is G-autonomous with respect to B; 2) B is a G-cause of A. The degree of G-emergence is calculated by multiplying the degree of A's G-autonomous by the degree of B's average G-cause.
The G-emergence theory proposed by Seth is the first attempt to use causal measures to quantify emergence phenomena. However, the causal relationship used by the author is Granger causality, which is not a strict causal relationship. At the same time, the measurement results also depend on the regression method used. In addition, the measurement index of this method is defined according to variables rather than dynamics, which means that the results will depend on the choice of variables. These all constitute the drawbacks of the G-emergence theory.
The causal emergence framework also has similarities with the aforementioned G-emergence. The macroscopic states of both methods need to be manually selected. In addition, it should be noted that some of the above methods for quantitatively quantifying emergence often do not consider true interventionist causality.
Other theories for quantitatively characterizing emergence
In addition, there are some other quantitative theories of emergence. There are mainly two methods that are widely discussed. One is to understand emergence from the process from disorder to order. Moez Mnif and Christian Müller-Schloer [30] use Shannon entropy to measure order and disorder. In the self-organization process, emergence occurs when order increases. The increase in order is calculated by measuring the difference in Shannon entropy between the initial state and the final state. However, the defect of this method is that it depends on the abstract observation level and the initial conditions of the system. To overcome these two difficulties, the authors propose a measurement method compared with the maximum entropy distribution. Inspired by the work of Moez mif and Christian Müller-Schloer, reference [31] suggests using the divergence between two probability distributions to quantify emergence. They understand emergence as an unexpected or unpredictable distribution change based on the observed samples. But this method has disadvantages such as large computational complexity and low estimation accuracy. To solve these problems, reference [32] further proposes an approximate method for estimating density using Gaussian mixture models and introduces Mahalanobis distance to characterize the difference between data and Gaussian components, thus obtaining better results. In addition, Holzer and de Meer [33][34] and others proposed another emergence measurement method based on Shannon entropy. They believe that a complex system is a self-organizing process in which different individuals interact through communication. Then, we can measure emergence according to the ratio between the Shannon entropy measure of all communications between agents and the sum of Shannon entropies as separate sources.
Another method is to understand emergence from the perspective of "the whole is greater than the sum of its parts" [35][36]. This method defines emergence from interaction rules and the states of agents rather than statistically measuring from the totality of the entire system. Specifically, this measure consists of subtracting two terms. The first term describes the collective state of the entire system, while the second term represents the sum of the individual states of all components. This measure emphasizes that emergence arises from the interactions and collective behavior of the system.
Causal emergence theory based on effective information
In history, the first relatively complete and explicit quantitative theory that uses causality to define emergence is the causal emergence theory proposed by Erik Hoel, Larissa Albantakis, and Giulio Tononi [1][2]. This theory defines so-called causal emergence for Markov chains as the phenomenon that the coarsened Markov chain has a greater causal effect strength than the original Markov chain. Here, the causal effect strength is measured by effective information. This indicator is a modification of the mutual information indicator. The main difference is that the state variable at time $t$ is intervened by do-intervention and transformed into a uniform distribution (or maximum entropy distribution). The effective information indicator was proposed by Giulio Tononi as early as 2003 when studying integrated information theory. As Giulio Tononi's student, Erik Hoel applied effective information to Markov chains and proposed the causal emergence theory based on effective information.
Causal Emergence Theory Based on Information Decomposition
In addition, in 2020, Rosas et al. proposed a method based on information decomposition to define causal emergence in systems from an information theory perspective and quantitatively characterize emergence based on synergistic information or redundant information. The so-called information decomposition is a new method to analyze the complex interrelationships of various variables in complex systems. By decomposing information, each partial information is represented by an information atom. At the same time, each partial information is projected into the information atom with the help of an information lattice diagram. Both synergistic information and redundant information can be represented by corresponding information atoms. This method is based on the non-negative decomposition theory of multivariate information proposed by Williams and Beer. In the paper, partial information decomposition (PID) is used to decompose the mutual information between microstates and macrostates. However, the PID framework can only decompose the mutual information between multiple source variables and one target variable. Rosas extended this framework and proposed the integrated information decomposition method [math]\displaystyle{ \Phi ID }[/math].
Recent Work
Barnett et al. [40] proposed the concept of dynamical decoupling by judging the decoupling of macroscopic and microscopic dynamics based on transfer entropy to judge the occurrence of emergence. That is, emergence is characterized as the macroscopic variables and microscopic variables being independent of each other and having no causal relationship, which can also be regarded as a causal emergence phenomenon. In 2024, Zhang Jiang et al. [26] proposed a new causal emergence theory based on singular value decomposition. The core idea of this theory is to point out that the so-called causal emergence is actually equivalent to the emergence of dynamical reversibility. Given the Markov transition matrix of a system, by performing singular value decomposition on it, the sum of the [math]\displaystyle{ \alpha }[/math] power of the singular values is defined as the reversibility measure of Markov dynamics ([math]\displaystyle{ \Gamma_{\alpha}\equiv \sum_{i=1}^N\sigma_i^{\alpha} }[/math]), where [math]\sigma_i[/math] is the singular value. This index is highly correlated with effective information and can also be used to characterize the causal effect strength of dynamics. According to the spectrum of singular values, this method can directly define the concepts of clear emergence and vague emergence without explicitly defining a coarse-graining scheme.
Quantification of causal emergence
Next, we will focus on introducing several studies that use causal measures to quantify emergence phenomena.
Several causal emergence theories
How to define causal emergence is a key issue. There are several representative works, namely the method based on effective information proposed by Hoel et al. [1][2], the method based on information decomposition proposed by Rosas et al. [37], a new causal emergence theory based on singular value decomposition proposed by Zhang Jiang et al. [26], and some other theories.
Erik Hoel's causal emergence theory
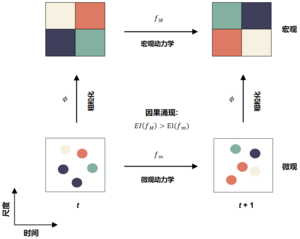
In 2013, Hoel et al. [1][2] proposed the causal emergence theory. The following figure is an abstract framework for this theory. The horizontal axis represents time and the vertical axis represents scale. This framework can be regarded as a description of the same dynamical system on both microscopic and macroscopic scales. Among them, [math]f_m[/math] represents microscopic dynamics, [math]f_M[/math] represents macroscopic dynamics, and the two are connected by a coarse-graining function [math]\phi[/math]. In a discrete-state Markov dynamical system, both [math]f_m[/math] and [math]f_M[/math] are Markov chains. By performing coarse-graining of the Markov chain on [math]f_m[/math], [math]f_M[/math] can be obtained. [math]\displaystyle{ EI }[/math] is a measure of effective information. Since the microscopic state may have greater randomness, which leads to relatively weak causality of microscopic dynamics, by performing reasonable coarse-graining on the microscopic state at each moment, it is possible to obtain a macroscopic state with stronger causality. The so-called causal emergence refers to the phenomenon that when we perform coarse-graining on the microscopic state, the effective information of macroscopic dynamics will increase, and the difference in effective information between the macroscopic state and the microscopic state is defined as the intensity of causal emergence.
Effective Information
Effective Information ([math]\displaystyle{ EI }[/math]) was first proposed by Tononi et al. in the study of integrated information theory [41]. In causal emergence research, Erik Hoel and others use this causal effect measure index to quantify the strength of causality of a causal mechanism.
Specifically, the calculation of [math]\displaystyle{ EI }[/math] is as follows: use an intervention operation to intervene on the independent variable and examine the mutual information between the cause and effect variables under this intervention. This mutual information is effective information, that is, the causal effect measure of the causal mechanism.
In a Markov chain, the state variable [math]X_t[/math] at any time can be regarded as the cause, and the state variable [math]X_{t + 1}[/math] at the next time can be regarded as the result. Thus, the state transition matrix of the Markov chain is its causal mechanism. Therefore, the calculation formula for [math]\displaystyle{ EI }[/math] for a Markov chain is as follows:
[math]\displaystyle{ \begin{aligned} EI(f) \equiv& I(X_t,X_{t+1}|do(X_t)\sim U(\mathcal{X}))\equiv I(\tilde{X}_t,\tilde{X}_{t+1}) \\ &= \frac{1}{N}\sum^N_{i=1}\sum^N_{j=1}p_{ij}\log\frac{N\cdot p_{ij}}{\sum_{k=1}^N p_{kj}} \end{aligned} }[/math]
Here [math]\displaystyle{ f }[/math] represents the state transition matrix of a Markov chain, [math]U(\mathcal{X})[/math] represents the uniform distribution on the value space [math]\mathcal{X}[/math] of the state variable [math]X_t[/math]. [math]\displaystyle{ \tilde{X}_t,\tilde{X}_{t+1} }[/math] are the states at two consecutive moments after intervening [math]X_t[/math] at time [math]\displaystyle{ t }[/math] into a uniform distribution. [math]\displaystyle{ p_{ij} }[/math] is the transition probability from the [math]\displaystyle{ i }[/math]-th state to the [math]\displaystyle{ j }[/math]-th state. From this formula, it is not difficult to see that [math]\displaystyle{ EI }[/math] is only a function of the probability transition matrix [math]f[/math]. The intervention operation is performed to make the effective information objectively measure the causal characteristics of the dynamics without being affected by the distribution of the original input data.
Effective information can be decomposed into two parts: determinism and degeneracy. Normalization can also be introduced to eliminate the influence of the size of the state space. For more detailed information about effective information, please refer to the entry: Effective Information.
Causal Emergence Measurement
We can judge the occurrence of causal emergence by comparing the magnitudes of effective information of macroscopic and microscopic dynamics in the system:
[math]\displaystyle{ CE = EI\left ( f_M \right ) - EI\left (f_m \right ) }[/math]
Here [math]\displaystyle{ CE }[/math] is the causal emergence intensity. If the effective information of macroscopic dynamics is greater than that of microscopic dynamics (that is, [math]\displaystyle{ CE\gt 0 }[/math]), then we consider that macroscopic dynamics has causal emergence characteristics on the basis of this coarse-graining.
Markov Chain Example
In the literature [1], Hoel gives an example of a state transition matrix ([math]f_m[/math]) of a Markov chain with 8 states, as shown in the left figure below. Among them, the first 7 states transfer with equal probability, and the last state is independent and can only transition to its own state.
The coarse-graining of this matrix is as follows: First, merge the first 7 states into a macroscopic state, which may be called A. And sum up the probability values in the first 7 columns of the first 7 rows in [math]f_m[/math] to obtain the probability of state transition from macroscopic state A to state A, and keep other values of the [math]f_m[/math] matrix unchanged. The new probability transition matrix after merging is shown in the right figure, denoted as [math]f_M[/math]. This is a definite macroscopic Markov transition matrix, that is, the future state of the system can be completely determined by the current state. At this time [math]\displaystyle{ EI(f_M)\gt EI(f_m) }[/math], and causal emergence occurs in the system.
Boolean Network Example
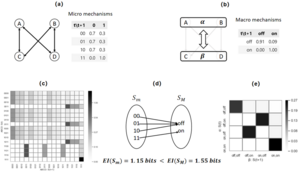
Another example in the literature [1] is an example of causal emergence in a Boolean network. As shown in the figure, this is a Boolean network with 4 nodes. Each node has two states, 0 and 1. Each node is connected to two other nodes and follows the same microscopic dynamics mechanism (figure a). Therefore, this system contains a total of sixteen microscopic states, and its dynamics can be represented by a state transition matrix (figure c).
The coarse-graining operation of this system is divided into two steps. The first step is to cluster the nodes in the Boolean network. As shown in figure b below, merge A and B to obtain the macroscopic node [math]\alpha[/math], and merge C and D to obtain the macroscopic node [math]\beta[/math]. The second step is to map the microscopic node states in each group to the merged macroscopic node states. This mapping function is shown in figure d below. All microscopic node states containing 0 are transformed into the off state of the macroscopic node, while the microscopic 11 state is transformed into the on state of the macroscopic. In this way, we can obtain a new macroscopic Boolean network, and obtain the dynamic mechanism of the macroscopic Boolean network according to the dynamic mechanism of the microscopic nodes. According to this mechanism, the state transition matrix of the macroscopic network can be obtained (as shown in figure e).
Through comparison, we find that the effective information of macroscopic dynamics is greater than that of microscopic dynamics [math]\displaystyle{ EI(f_M\ )\gt EI(f_m\ ) }[/math]. Causal emergence occurs in this system.
Causal Emergence in Continuous Variables
Furthermore, in the paper [42], Hoel et al. proposed the theoretical framework of causal geometry, trying to generalize the causal emergence theory to function mappings and dynamical systems with continuous states. This article defines [math]\displaystyle{ EI }[/math] for random function mapping, and also introduces the concepts of intervention noise and causal geometry, and compares and analogizes this concept with information geometry. Liu Kaiwei et al.[43] further gave an exact analytical causal emergence theory for random iterative dynamical systems.
Rosas's Causal Emergence Theory
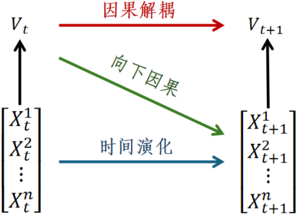
Rosas et al. [37] From the perspective of information decomposition theory, propose a method for defining causal emergence based on integrated information decomposition, and further divide causal emergence into two parts: causal decoupling (Causal Decoupling) and downward causation (Downward Causation). Among them, causal decoupling represents the causal effect of the macroscopic state at the current moment on the macroscopic state at the next moment, and downward causation represents the causal effect of the macroscopic state at the previous moment on the microscopic state at the next moment. The schematic diagrams of causal decoupling and downward causation are shown in the following figure. The microscopic state input is [math]\displaystyle{ X_t\ (X_t^1,X_t^2,…,X_t^n ) }[/math], and the macroscopic state is [math]\displaystyle{ V_t }[/math], which is obtained by coarse-graining the microscopic state variable [math]\displaystyle{ X_t }[/math], so it is a supervenient feature of [math]\displaystyle{ X_t }[/math], [math]\displaystyle{ X_{t + 1} }[/math] and [math]\displaystyle{ V_{t + 1} }[/math] represent the microscopic and macroscopic states at the next moment respectively.
Partial Information Decomposition
This method is based on the nonnegative decomposition of multivariate information theory proposed by Williams and Beer et al [44]. This paper uses partial information decomposition (PID) to decompose the mutual information between microstates and macrostates.
Without loss of generality, assume that our microstate is [math]\displaystyle{ X(X^1,X^2) }[/math], that is, it is a two-dimensional variable, and the macrostate is [math]\displaystyle{ V }[/math]. Then the mutual information between the two can be decomposed into four parts:
[math]\displaystyle{ I(X^1,X^2;V)=Red(X^1,X^2;V)+Un(X^1;V│X^2)+Un(X^2;V│X^1)+Syn(X^1,X^2;V) }[/math]
Among them, [math]\displaystyle{ Red(X^1,X^2;V) }[/math] represents redundant information, which refers to the information repeatedly provided by two microstates [math]\displaystyle{ X^1 }[/math] and [math]\displaystyle{ X^2 }[/math] to the macrostate [math]\displaystyle{ V }[/math]; [math]\displaystyle{ Un(X^1;V│X^2) }[/math] and [math]\displaystyle{ Un(X^2;V│X^1) }[/math] represent unique information, which refers to the information provided by each microstate variable alone to the macrostate; [math]\displaystyle{ Syn(X^1,X^2;V) }[/math] represents synergistic information, which refers to the information provided by all microstates [math]\displaystyle{ X }[/math] jointly to the macrostate [math]\displaystyle{ V }[/math].
Definition of Causal Emergence
However, the PID framework can only decompose the mutual information between multiple source variables and one target variable. Rosas extended this framework and proposed the integrated information decomposition method [math]\displaystyle{ \Phi ID }[/math][45] to handle the mutual information between multiple source variables and multiple target variables. It can also be used to decompose the mutual information between different moments. Based on the decomposed information, the author proposed two definition methods of causal emergence:
1) When the unique information [math]\displaystyle{ Un(V_t;X_{t + 1}|X_t^1,\ldots,X_t^n\)\gt 0 }[/math], it means that the macroscopic state [math]\displaystyle{ V_t }[/math] at the current moment can provide more information to the overall system [math]\displaystyle{ X_{t + 1} }[/math] at the next moment than the microscopic state [math]\displaystyle{ X_t }[/math] at the current moment. At this time, there is causal emergence in the system;
2) The second method bypasses the selection of a specific macroscopic state [math]\displaystyle{ V_t }[/math], and defines causal emergence only based on the synergistic information between the microscopic state [math]\displaystyle{ X_t }[/math] and the microscopic state [math]\displaystyle{ X_{t + 1} }[/math] at the next moment of the system. When the synergistic information [math]\displaystyle{ Syn(X_t^1,…,X_t^n;X_{t + 1}^1,…,X_{t + 1}^n)\gt 0 }[/math], causal emergence occurs in the system.
It should be noted that for the first method to judge the occurrence of causal emergence, it depends on the selection of the macroscopic state [math]\displaystyle{ V_t }[/math]. The first method is the lower bound of the second method. This is because [math]\displaystyle{ Syn(X_t;X_{t + 1}\)≥Un(V_t;X_{t + 1}|X_t) }[/math] always holds. So, if [math]\displaystyle{ Un(V_t;X_{t + 1}|X_t) }[/math] is greater than 0, then causal emergence occurs in the system. However, the selection of [math]\displaystyle{ V_t }[/math] often requires predefining a coarse-graining function, so the limitations of the Erik Hoel causal emergence theory cannot be avoided. Another natural idea is to use the second method to judge the occurrence of causal emergence with the help of synergistic information. However, the calculation of synergistic information is very difficult and there is a combinatorial explosion problem. Therefore, the calculation based on synergistic information in the second method is often infeasible. In short, both quantitative characterization methods of causal emergence have some weaknesses, so a more reasonable quantification method needs to be proposed.
Specific Example
The author of the paper [37] lists a specific example (as above), to illustrate when causal decoupling, downward causation and causal emergence occur. This example is a special Markov process. Here, [math]\displaystyle{ p_{X_{t + 1}|X_t}(x_{t + 1}|x_t) }[/math] represents the dynamic relationship, and [math]\displaystyle{ X_t=(x_t^1,…,x_t^n)\in\{0,1\}^n }[/math] is the microstate. The definition of this process is to determine the probability of taking different values of the state [math]\displaystyle{ x_{t + 1} }[/math] at the next moment by checking the values of the variables [math]\displaystyle{ x_t }[/math] and [math]\displaystyle{ x_{t + 1} }[/math] at two consecutive moments, that is, judging whether the sum modulo 2 of all dimensions of [math]\displaystyle{ x_t }[/math] is the same as the first dimension of [math]\displaystyle{ x_{t + 1} }[/math]: if they are different, the probability is 0; otherwise, judge whether [math]\displaystyle{ x_t,x_{t + 1} }[/math] have the same sum modulo 2 value in all dimensions. If both conditions are satisfied, the value probability is [math]\displaystyle{ \gamma/2^{n - 2} }[/math], otherwise the value probability is [math]\displaystyle{ (1-\gamma)/2^{n - 2} }[/math]. Here [math]\displaystyle{ \gamma }[/math] is a parameter and [math]\displaystyle{ n }[/math] is the total dimension of x.
In fact, if [math]\displaystyle{ \sum_{j = 1}^n x^j_t }[/math] is even or 0, then [math]\displaystyle{ \oplus^n_{j = 1} x^j_t:=1 }[/math], otherwise [math]\displaystyle{ \oplus^n_{j = 1} x^j_t:=0 }[/math]. Therefore, the result of [math]\displaystyle{ \oplus^n_{j = 1} x^j_t }[/math] is the parity of the entire X sequence, and the first dimension can be regarded as a parity check bit. [math]\displaystyle{ \gamma }[/math] actually represents the probability that a mutation occurs in two bits of the X sequence, and this mutation can ensure that the parity of the entire sequence remains unchanged, and the parity check bit of the sequence also conforms to the actual parity of the entire sequence.
Therefore, the macroscopic state of this process can be regarded as the parity of the sum of all dimensions of the entire sequence, and the probability distribution of this parity is the result of the exclusive OR calculation of the microstate. [math]\displaystyle{ x_{t + 1}^1 }[/math] is a special microstate that always remains consistent with the macroscopic state of the sequence at the previous moment. Therefore, when only the first item in the second judgment condition is satisfied, the downward causation condition of the system occurs. When only the second item is satisfied, the causal decoupling of the system occurs. When both items are satisfied simultaneously, it is said that causal emergence occurs in the system.
Causal Emergence Theory Based on Singular Value Decomposition
Erik Hoel's causal emergence theory has the problem of needing to specify a coarse-graining strategy in advance. Rosas' information decomposition theory does not completely solve this problem. Therefore, Zhang Jiang et al.[26] further proposed the causal emergence theory based on singular value decomposition.
Singular Value Decomposition of Markov Chains
Given the Markov transition matrix [math]\displaystyle{ P }[/math] of a system, we can perform singular value decomposition on it to obtain two orthogonal and normalized matrices [math]\displaystyle{ U }[/math] and [math]\displaystyle{ V }[/math], and a diagonal matrix [math]\displaystyle{ \Sigma }[/math]: [math]\displaystyle{ P = U\Sigma V^T }[/math], where [math]\Sigma = diag(\sigma_1,\sigma_2,\cdots,\sigma_N)[/math], where [math]\sigma_1\geq\sigma_2\geq\cdots\sigma_N[/math] are the singular values of [math]\displaystyle{ P }[/math] and are arranged in descending order. [math]\displaystyle{ N }[/math] is the number of states of [math]\displaystyle{ P }[/math].
Approximate Dynamical Reversibility and Effective Information
We can define the sum of the [math]\displaystyle{ \alpha }[/math] powers of the singular values (also known as the [math]\alpha[/math]-order Schatten norm of the matrix) as a measure of the approximate dynamical reversibility of the Markov chain, that is:
[math]\displaystyle{ \Gamma_{\alpha}\equiv \sum_{i = 1}^N\sigma_i^{\alpha} }[/math]
Here, [math]\alpha\in(0,2)[/math] is a specified parameter that acts as a weight or tendency to make [math]\Gamma_{\alpha}[/math] reflect determinism or degeneracy more. Under normal circumstances, we take [math]\alpha = 1[/math>, which can make [math]\Gamma_{\alpha}[/math> achieve a balance between determinism and degeneracy.
In addition, the authors in the literature prove that there is an approximate relationship between [math]\displaystyle{ EI }[/math] and [math]\Gamma_{\alpha}[/math>:
[math]\displaystyle{ EI\sim \log\Gamma_{\alpha} }[/math]
Moreover, to a certain extent, [math]\Gamma_{\alpha}[/math> can be used instead of EI to measure the degree of causal effect of Markov chains. Therefore, the so-called causal emergence can also be understood as an emergence of dynamical reversibility.
Quantification of Causal Emergence without Coarse-graining
However, the greatest value of this theory lies in the fact that emergence can be directly quantified without a coarse-graining strategy. If the rank of [math]\displaystyle{ P }[/math] is [math]\displaystyle{ r }[/math], that is, starting from the [math]\displaystyle{ r + 1 }[/math]th singular value, all singular values are 0, then we say that the dynamics [math]\displaystyle{ P }[/math] has clear causal emergence, and the numerical value of causal emergence is:
[math]\displaystyle{ \Delta \Gamma_{\alpha} = \Gamma_{\alpha}(1/r - 1/N) }[/math]
If the matrix [math]\displaystyle{ P }[/math] is full rank, but for any given small number [math]\displaystyle{ \epsilon }[/math], there exists [math]\displaystyle{ r_{\epsilon} }[/math] such that starting from [math]\displaystyle{ r_{\epsilon}+1 }[/math], all singular values are less than [math]\displaystyle{ \epsilon }[/math], then it is said that the system has a degree of vague causal emergence, and the numerical value of causal emergence is:
[math]\displaystyle{ \Delta \Gamma_{\alpha}(\epsilon) = \frac{\sum_{i = 1}^{r} \sigma_{i}^{\alpha}}{r} - \frac{\sum_{i = 1}^{N} \sigma_{i}^{\alpha}}{N} }[/math]
In summary, the advantage of this method for quantifying causal emergence is that it can quantify causal emergence more objectively without relying on a specific coarse-graining strategy. The disadvantage of this method is that to calculate [math]\Gamma_{\alpha}[/math], it is necessary to perform SVD decomposition on [math]\displaystyle{ P }[/math] in advance, so the computational complexity is [math]O(N^3)[/math], which is higher than the computational complexity of [math]\displaystyle{ EI }[/math]. Moreover, [math]\Gamma_{\alpha}[/math> cannot be explicitly decomposed into two components: determinism and degeneracy.
Specific Example
The author gives four specific examples of Markov chains. The state transition matrix of this Markov chain is shown in the figure. We can compare the [math]\displaystyle{ EI }[/math] and approximate dynamical reversibility (the [math]\displaystyle{ \Gamma }[/math] in the figure, that is, [math]\displaystyle{ \Gamma_{\alpha = 1} }[/math]) of this Markov chain. Comparing figures a and b, we find that for different state transition matrices, when [math]\displaystyle{ EI }[/math] decreases, [math]\displaystyle{ \Gamma }[/math] also decreases simultaneously. Further, figures c and d are comparisons of the effects before and after coarse-graining. Among them, figure d is the coarse-graining of the state transition matrix of figure c (merging the first three states into a macroscopic state). Since the macroscopic state transition matrix in figure d is a deterministic system, the normalized [math]\displaystyle{ EI }[/math], [math]\displaystyle{ eff\equiv EI/\log N }[/math] and the normalized [math]\Gamma[/math>: [math]\displaystyle{ \gamma\equiv \Gamma/N }[/math] all reach the maximum value of 1.

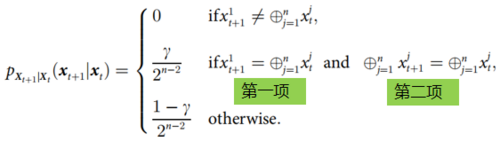
![[math]\displaystyle{ EI }[/math]与[math]\displaystyle{ \Gamma }[/math]对比](/images/thumb/0/03/Gamma%E4%BE%8B%E5%AD%90.png/500px-Gamma%E4%BE%8B%E5%AD%90.png)