动力学的一致性检验

在复杂网络中的因果涌现词条中我们介绍了如何对一个复杂网络进行粗粒化。好的粗粒化方案是能够保证原始的网络（或转移矩阵）和粗粒化后的网络（或转移矩阵）尽可能地相似的，那么如何保证这种相似性呢？Klein等人在论文提出了一种动力学一致性检验方法，它的基本思想是通过比较粗粒化方案后未曾被分组归并的节点上的概率分布是否和原始的网络一致（用KL散度来刻画）来判断粗粒化方案的好坏。此外，需要注意的是该方法适用于仅针对一组节点进行归并的情形，当应用于多个分组归并时，则该方法可能难以执行。

计算动力学的一致性检验的具体步骤如下：

输入：微观网络[math]\displaystyle{ A }[/math]，宏观网络[math]\displaystyle{ B }[/math]以及总的转移时间步[math]\displaystyle{ T }[/math]；输出：动力学的不一致性（inconsistency）

1. 初始化一个微观分布[math]\displaystyle{ S_m(0) }[/math]（分布长度和微观网络的大小一致，记为N），将分布中没有进行粗粒化的节点位置设为1，其余位置设为0；初始化一个宏观分布[math]\displaystyle{ S_M(0) }[/math]（分布长度和宏观网络的大小一致，记为M），同样将分布中还是原始微观网络中的节点位置设为1（分布中值为1的数量为Z），其余位置设为0；基于网络[math]\displaystyle{ A }[/math]和[math]\displaystyle{ B }[/math]分别得到转移概率矩阵[math]\displaystyle{ W_A }[/math]和[math]\displaystyle{ W_B }[/math]
2. 从1到T步迭代t，每一步完成如下步骤：
   1. [math]\displaystyle{ S_m(t) = (W_A^t)^T S_m(0) }[/math]，其中[math]\displaystyle{ W_A^t }[/math]表示[math]\displaystyle{ W_A }[/math]自乘t次，即t步转移的概率转移矩阵;
   2. 对[math]\displaystyle{ S_m(t) }[/math]进行归一化；
   3. 初始化一个长度为Z+1的分布[math]\displaystyle{ P_{M|m}(t) }[/math]，表示微观节点分布叠加到相同宏观节点上的概率分布，其中[math]\displaystyle{ P_{M|m}(t) }[/math]的前Z个位置的数值等于[math]\displaystyle{ S_m(t) }[/math]中对应的Z个没有进行粗粒化的节点位置的值，[math]\displaystyle{ P_{M|m}(t) }[/math]中的第Z+1位置的数值等于[math]\displaystyle{ 1-\sum_{i=1}^Z p^i_{M|m}(t) }[/math]
   4. [math]\displaystyle{ S_M(t) = (W_B^t)^T S_M(0) }[/math]，其中[math]\displaystyle{ W_B^t }[/math]表示[math]\displaystyle{ W_B }[/math]自乘t次，即t步转移的概率转移矩阵;
   5. 对[math]\displaystyle{ S_M(t) }[/math]进行归一化;
   6. 初始化一个长度为Z+1的分布[math]\displaystyle{ P_M(t) }[/math]，表示宏观节点的概率分布, 其中[math]\displaystyle{ P_M(t) }[/math]的前Z个位置的数值等于[math]\displaystyle{ S_M(t) }[/math]中对应的Z个没有进行粗粒化的节点位置的值，[math]\displaystyle{ P_M(t) }[/math]中的第Z+1位置的数值等于[math]\displaystyle{ 1-\sum_{i=1}^Z p^i_M(t) }[/math]
3. 使用[math]\displaystyle{ P_M(t) }[/math]和[math]\displaystyle{ P_{M|m}(t) }[/math]之间的KL散度来衡量其不一致性，若结果为零则动力学一致， 公式为：[math]\displaystyle{ inconsistency=\sum_{t=1}^T D_{KL}[P_{M|m}(t)||P_M(t)] }[/math]

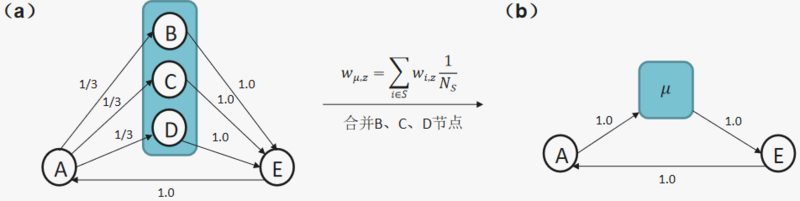
为了展示具体动力学一致性的计算流程，我们给出一个具体例子，例子如下所示，图a是微观网络，含有5个节点，其中B、C和D为待合并节点，图b是宏观网络，将节点B，C，D粗粒化成一个宏观节点[math]\displaystyle{ \mu }[/math]，下图中的[math]\displaystyle{ w_{\mu,z} }[/math]表示宏观网络中节点[math]\displaystyle{ \mu }[/math]和节点[math]\displaystyle{ z }[/math]之间的转移概率，[math]\displaystyle{ w_{i,z} }[/math]表示微观网络中的节点[math]\displaystyle{ i }[/math]和节点[math]\displaystyle{ z }[/math]之间的转移概率，[math]\displaystyle{ Ns }[/math]为待合并节点的数量。

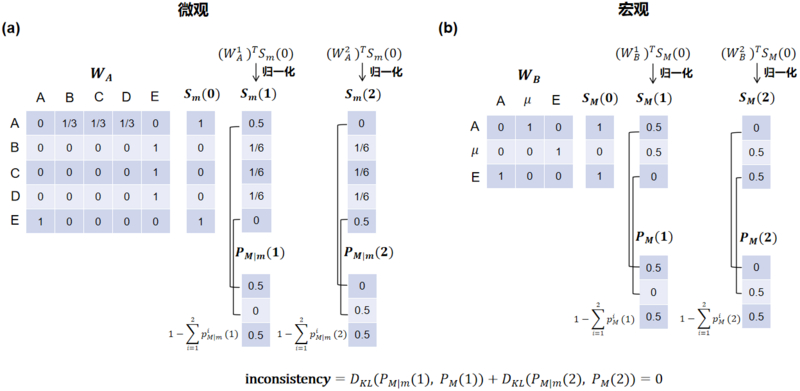
下图我们给了针对上面例子是如何计算动力学一致性的详细步骤，该例子中我们设置[math]\displaystyle{ T=2 }[/math]，图a和图b分别是微观和宏观网络的期望分布的计算过程。计算出来的[math]\displaystyle{ inconsistency=0 }[/math]，满足动力学一致性。

此外，其他实验中也发现，针对偏好依附网络来说，在不同节点规模以及参数下的粗粒化后的宏观网络的不一致性会随着迭代步数的增加都会收敛到0。