基于高阶依赖项建模的节点归并方法

下面我们介绍基于高阶依赖项建模的节点归并方法

通过网络粗粒化方法可以对节点进行分组，为了构建粗粒化后的宏观网络，需要将微观节点合并成宏观节点，同时需要计算宏观网络之间的连边，以及对应的转移概率。在上述三种方法中，前两种都使用了一种叫做高阶依赖项建模(HOMs)的方法来进行归并，其目的是为了保证分组后的宏观网络和原始网络具有相似的随机游走动力学。

具体来说，不同类型的微观节点合并成宏观节点时转移概率有不同的处理方式：

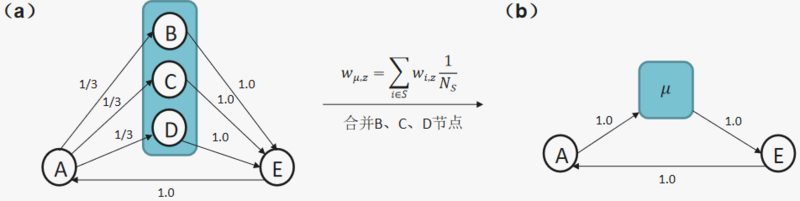
1）下面图a展示了微观网络，其中待合并的节点（节点B，C，D）之间没有连边，且待合并节点都指向相同的输出节点（节点E），将节点B，C，D粗粒化成一个宏观节点[math]\displaystyle{ \mu }[/math]，如图b所示，同时需要将指向待合并节点的概率相加，待合并节点的输出概率取平均，具体宏观节点输出概率计算方法为：[math]\displaystyle{ w_{\mu,z}=\sum_{i \in S}w_{i,z}\frac{1}{N_S} }[/math]，其中[math]\displaystyle{ S }[/math]表示待合并节点集合，节点[math]\displaystyle{ i }[/math]表示待合并节点集合中的节点（如下图中的节点B，C，D），节点[math]\displaystyle{ z }[/math]表示待合并节点指向的节点（如下图中的节点E），[math]\displaystyle{ w_{i,z} }[/math]表示微观网络中的节点[math]\displaystyle{ i }[/math]和节点[math]\displaystyle{ z }[/math]之间的转移概率，[math]\displaystyle{ w_{\mu,z} }[/math]表示宏观网络中节点[math]\displaystyle{ \mu }[/math]和节点[math]\displaystyle{ z }[/math]之间的转移概率，[math]\displaystyle{ Ns }[/math]为待合并节点的数量；

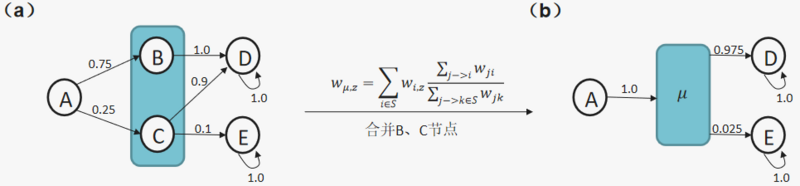
2）下面图a展示了待合并的节点（节点B，C）之间没有连边但是待合并节点指向多个输出节点的情况（节点D和E），将节点B，C粗粒化成一个宏观节点[math]\displaystyle{ \mu }[/math]，图b展示了对应的宏观网络，边权处理方式：需要将指向待合并节点的概率相加，待合并节点的输出概率按比例加权求和，具体宏观节点输出概率计算方法为：[math]\displaystyle{ w_{\mu,z}=\sum_{i \in S}w_{i,z}\frac{\sum_{j\rightarrow i}w_{ji}}{\sum_{j\rightarrow k\in S}w_{jk}} }[/math]，其中，[math]\displaystyle{ j\rightarrow i }[/math]表示节点j（如下面图a中的A节点）指向待合并节点集合中的节点i的边，[math]\displaystyle{ w_{\mu,z} }[/math]表示宏观网络中节点[math]\displaystyle{ \mu }[/math]和节点[math]\displaystyle{ z }[/math]之间的转移概率，这里[math]\displaystyle{ z }[/math]表示待合并节点指向的节点（如图a中的节点E）；

3）下面图a展示了待合并的节点（节点B，C）之间存在连边且待合并节点指向多个输出节点的情况（节点D和E），如图a所示，将节点B，C粗粒化成一个宏观节点[math]\displaystyle{ \mu }[/math]，图b展示了对应的宏观网络，具体宏观节点输出概率计算方法为：[math]\displaystyle{ w_{\mu,z}=\sum_{i \in S}w_{i,z}\frac{\pi_i}{\sum_{k\in S}\pi_k} }[/math]，其中 [math]\displaystyle{ \pi_i }[/math]为节点[math]\displaystyle{ i }[/math]在节点平稳分布中的值，[math]\displaystyle{ w_{\mu,z} }[/math]表示宏观网络中节点[math]\displaystyle{ \mu }[/math]和节点[math]\displaystyle{ z }[/math]之间的转移概率；

4）更为复杂的情况，如下图a所示，待合并的节点(B，C，D)三者之间存在循环结构，需要综合考虑方法2和方法3，将待合并的节点粗粒化为两个宏观节点[math]\displaystyle{ \mu_1 }[/math]和[math]\displaystyle{ \mu_2 }[/math]，来捕获延迟效果，其中宏观节点[math]\displaystyle{ \mu_1 }[/math]起到缓冲的效果，最终[math]\displaystyle{ \mu_1 }[/math]和[math]\displaystyle{ \mu_2 }[/math]组成的宏观节点具有记忆功能，如图b所示，宏观节点的转移概率同样结合方法2和方法3进行计算。具体计算时做了简化，[math]\displaystyle{ \mu_1 }[/math]和[math]\displaystyle{ \mu_2 }[/math]之间的转移概率设为1，[math]\displaystyle{ \mu_2 }[/math]的转移概率按照方法3进行计算；

由于本质上上面提出的复杂网络的合并方式是对马尔科夫链进行粗粒化，我们也可以参考TPM的粗粒化方法，具体参考马尔科夫链的粗粒化词条。