PageRank算法
PageRank(PR)算法,又称为网页排名算法, Google左侧排算法。Page Rank得名为谷歌创始人之一拉里佩奇(Larry Page).PageRank是一种衡量网站页面重要性的方法。根据谷歌的说法: PageRank通过计算页面链接的数量和质量来粗略估计分析网站的重要性。基本假设是:更重要的页面往往更多地被其他页面引用(或称其他页面中会更多地加入通向该页面的超链接)
目前该算法不再是谷歌用于排序搜索结果的唯一算法,但它是谷歌公司使用的第一个排序搜索算算法,也是最著名的算法。截止至2019年9月24日,PageRank和所有的相关专利已过期。
描述
Page Rank是一种链接分析算法,它通过对超链接集合(如万维网)中的元素实现数值权重赋值,实现“衡量集合范围内某一元素的相关重要性”的目的。该算法可以应用于带有相互引用或者引用关系的任何实体集合。算法赋值给任何给定元素E的数值权重称为E的PageRank,并且用PR(E) 表示。 PageRank的结果来源于一种基于图论的数学算法。它将万维网上所有的网页视作节点(node),而将超链接视作边(edge),并且考虑到了一些权威的网站,类似cnn.com或者qq.com。每个节点的权重值表示对应的页面的重要度。通向该网页的超链接称做“对该网页的投票(a vote of support)”。每个网页的权重值大小被递归地定义,依托于所有链接该页面的页面的权重值。例如,一个被很多页面的链接的页面将会拥有较高的权重值(high PageRank)。
自Page和Brin(Google的另外一位创始人)的原始论文以来,已经发表了许多有关PageRank的学术论文。实际上,PageRank概念可能容易受到利用。相关的研究会关注那些因受到影响而出现错误的PageRank结果,以找到一种有效地避免其PageRank被错误影响的方法(如忽略部分错误的链接)。 PageRank算法中的点击算法是由乔恩·克莱因伯格(Jon Kleinberg)提出的。而其他的基于链接的网页排名算法有乔恩·克莱因伯格发明的HITS算法,IBM CLEVER Project,TrustRank算法以及hummingbird算法等等。
历史
拉里·佩奇(Larry Page)和谢尔盖·布林(Sergey Brin)于1996年在斯坦福大学开发了PageRank,这是关于一种新型搜索引擎研究项目的一部分。赫克托·加西亚·莫利纳(Hector Garcia-Molina),斯坦福大学计算机科学教授也是谢尔盖(Sergey)的导师,提供了页面排名算法开发的背景知识。谢尔盖·布林(Sergey Brin)的想法是,可以通过“链接流行度”(Link popularity)按层次结构对Web上的信息进行排序:网页的排名越高,链接就越多。该系统是在Scott Hassan和Alan Steremberg的帮助下开发的,Page和Brin都认为他们对Google的发展至关重要。Rajeev Motwani和Terry Winograd与Page和Brin共同撰写了有关该项目的第一篇论文,描述了PageRank和Google搜索引擎的初始原型。此后不久,Page和Brin创立了Google公司,谷歌搜索为其产品。PageRank目前虽然只是决定Google搜索结果排名的众多因素之一,但仍继续为所有Google搜索提供基础。
"PageRank"这个名字里面的"Page"来源于拉里佩奇(Larry Page),也源于网页(Web Page)一次。但是这项专利为斯坦福大学所有,作为交换,斯坦福大学拥有谷歌的180万股的股份。 PageRank收到引文分析(Citation analysis)研究的启发,这是20世纪50年代宾夕法尼亚大学的Eugene Garfield和Hyper Search和University of Padua的Massimo Marchiori。在PageRank被提出的同一年,Jon Kleinberg 发表了HITS的研究成果。 编者著:HITS也是一种网络重要性分析的算法,按照HITS算法,用户输入关键词后,算法对返回的匹配页面计算两种值,一种是枢纽值(Hub Scores),另一种是权威值(Authority Scores),这两种值是互相依存、互相影响的。所谓枢纽值,指的是页面上所有导出链接指向页面的权威值之和。权威值是指所有导入链接所在的页面中枢纽之和。
算法
PageRank的基本思想
PageRank是以Google创始人Larry Page的姓命名,也来源于网页(web page)中的Page,该算法于1999被提出来,用于测量网页的相对重要性(对网页进行排序)。
PageRank算法通过输出概率分布来体现某人随机地点击某个链接的概率。PageRank值(PR)可以在任何规模的文件(document)集合中计算得出,而每个链接都指向该集合中的某个特定文件。相关研究论文指出,在初次计算前,总概率将被均分到每个文件上,使得集合中的每个文件被访问的概率都是相同的。接下来在重复多次的计算(又称为“迭代”)中,算法将根据集合的实际情况不断调整PR值,使得其越来越接近最真实的理论值。
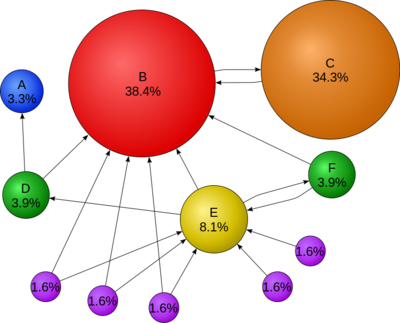
PageRank的设计受到学术论文引用启发。衡量一篇学术论文质量高与否,最重要的一个指标是引用次数,高引用量的论文通常意味着高质量。同理,如果一张网页被引用(以超链接的形式)多了,那么该网页就比较重要。总结起来,PageRank的核心思想有两点(结合图1说明): 越多的网页链接到一个网页(可以理解成投票,D --> B,D给B投了一票),说明这个网页更加重要,如图1的B。(一篇论文被很多论文引用) PageRank高的网页链接到一个网页,说明这张网页也很重要。如图1,尽管C只有一张网页B链接到它,但C的重要性高于E,尽管E有一堆小罗罗给它投票。(论文被大牛引用了,说明这篇论文很有价值)(也可以从话语权角度理解,重要的人说话份量重)
万维网(World Wide Web)可以抽象成一张有向图,节点表示网页,连线p_i -> p_j表示网页p_i包含了超链接p_j(p_i指向了p_j)。对图中每个节点的重要性进行量化,则就可以对网页进行排序。PageRank提出之初就是为了对网页进行排序。 搜索引擎的工作原理可以简化为:输入关键词,返回与该关键词相关的网页(一个集合,相当于得到一张子图),在该子图上计算每个节点的PageRank值,PageRank值高的网页排在前面,低的就排在后面。
计算PageRank
计算一个网页的[math]\displaystyle{ p_{i} }[/math]的PR值,则我们需要清楚两个信息:
- 有多少网页链接到了[math]\displaystyle{ p_{i} }[/math]
- 这些网页的PR值
其他网页的PR值很可能是依赖于[math]\displaystyle{ p_{i} }[/math]。这就陷入了一个循环,要想知道[math]\displaystyle{ p_{i} }[/math]的PR值,就得知道链向[math]\displaystyle{ p_{i} }[/math]所有网页的PR值,而要知道其他网页的PR值,又得先知道[math]\displaystyle{ p_{i} }[/math]的PR值。 为了打破这个循环,佩奇和布林采用了很巧妙的思路,他们分析一个虚拟用户在互联网上的漫游过程。 他们假定:虚拟用户一旦访问了一个网页,下一步将以相同的概率访问被该网页所链接的任何一个其它网页。比如,网页p_i包含了N个超链接,那么虚拟用户访问这N个页面中的任何一个的概率就是1。那么,网页的排序就可以堪称一个虚拟用户在万维网漫游了很长时间,页面被访问的概率越大,其PR值就越高,网页排名也越靠前。
简化的PageRank的例子
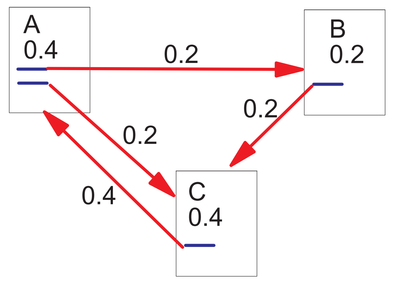
如图所示,每个节点初始化或者指定一个PageRank值(如PR(A)=0.4),网页A包含两个超链接,分别指向B和C(或者说A投票给B和C),0.4拆分成两份,每份0.2,所以PR(B)=0.2。A和B同时给C投票,所以PR(C)=0.2+0.2=0.4。如此,不断地迭代,最后每个节点的值都会收敛,这样就求得了所有节点的PR值。
每个页面将其当前的PageRank值平均分配到本页面所有出链上,一个页面将所有入链的PR值累加起来就构成了该页面新的PR值。如此迭代下去,最后得到一个稳定值。用数学公式表达,如下:
[math]\displaystyle{ PR(A) = \frac{PR(A)}{L(B)} + \frac{PR(C)}{L(C)} + \frac{PR(D)}{L(D)}+... }[/math]
推广到所有情况,B表示所有链向网页[math]\displaystyle{ p_{i} }[/math]的集合,则:
[math]\displaystyle{ \sum_{p_{j}\in B(p_{i})} \frac{PR(p_{j)}}{L(p_{j}} }[/math]
但是这样子有存在两个问题:
- 对于没有forward links (outedges)的网页,即只有别人给她投票,她从不给别人投票,那么她的PageRank每次迭代都会增加。
- 对于没有blacklinks (inedges)的网页,即没人给她投票,其PageRank永远等于0。
对于第一个问题,给等式乘以一个小于1的常数d(damping factor),这个常数被翻译成阻尼系数,意思为任意时刻浏览者访问到某页面后继续访问下一个页面的概率;对于第二个问题,给等式加上一个常数。新的等式如下(N表示网页总数,或者节点数目,本文中该公式成为PageRank基本公式,下同):
[math]\displaystyle{ PR(p_{i}) = \frac{1-d}{N}+d\sum _{p_{j}\in B(p_{i})}\frac{PR(p_{j}}{L(p_{j}} }[/math]
其中:
- [math]\displaystyle{ B(p_{i} }[/math]:链接到网页[math]\displaystyle{ p_{i} }[/math]的(a set of pages link to [math]\displaystyle{ p_{i} }[/math])。
- L(p_{j}):从[math]\displaystyle{ p_{j} }[/math]链出去的网页数目(the number of outbound links)。
这样子,所有的节点的PR值加起来就确保为1了。