图论

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
乐多多（讨论 | 贡献）2020年4月21日 (二) 16:44的版本 （→‎定义）
跳到导航 跳到搜索


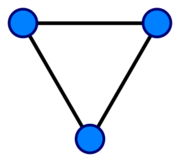
图论 Graph theory是指研究图和网络的数学分支，常被认为是组合数学 Combinatorial mathematics的一个分支，但这一分支已经发展得足够庞大和有特点，并有自身领域所研究的问题，因此被视为一个独立的主题。它和其他数学分支，如群论、矩阵论、拓扑学有着密切关系。图 graph是图论的主要研究对象。图是由若干给定的顶点及连接两顶点的边所构成的图形，这种图形通常用来描述某些事物之间的某种特定关系。顶点代表事物，连接两顶点的边则表示两个事物间具有这种关系。

市场中的关联关系：图形通常用来描述某些事物之间的某种特定关系。顶点代表事物，连接两顶点的边则表示两个事物间具有这种关系

定义

图论中有许多定义，以下是一些与之相关的最基本定义。

无向图

有三个顶点和三条边的图

图 graph通常定义为一个有序对 ordered pair [math]\displaystyle{ G=(V,E) }[/math]，[1][2]其中

  • [math]\displaystyle{ V }[/math] 是顶点 vertices/nodes/points的集合；
  • [math]\displaystyle{ E\subseteq\left\{\left\{x,y\right\}:(x,y)\in V^2,x\neq y\right\} }[/math] 是边 edges/links/lines的集合，边由所有顶点的无序对 ordered pair构成（换句话说，边连接了顶点对）。

为避免歧义，上面定义的对象可被更精准地称作无向简单图 undirected simple graph。

在边[math]\displaystyle{ { x,y } }[/math]中，顶点[math]\displaystyle{ x }[/math]和[math]\displaystyle{ y }[/math]称为边的端点 endpoints，边称为连接 join/incident on[math]\displaystyle{ x }[/math]和[math]\displaystyle{ y }[/math]。图中的某顶点可能不属于任意一条边。重边 Multiple edges/平行边 parallel edges是连接同一对顶点的两条或多条边。

允许重边时，上述定义可以推广：图是有序三元组 ordered triple [math]\displaystyle{ G=(V,E,\phi) }[/math]，[3][4] 其中

  • [math]\displaystyle{ V }[/math] 是点集；
  • [math]\displaystyle{ E }[/math] 是边集；
  • [math]\displaystyle{ \phi:E\to\left\{\left\{x,y\right\}:(x,y)\in V^2,x\neq y\right\} }[/math] 是一个将每条边映射到一个无序顶点对的关联函数 incidence function（于是边连接了顶点对）。

为避免歧义，上面定义的对象可被更精准地称作无向多重图 undirected multigraph。

自环 loop是连接顶点与自身的边，上述两个定义中的图不能有自环。为了允许自环，需要扩展定义。对于无向简单图，[math]\displaystyle{ E\subseteq\left\{\left\{x,y\right\}:(x,y)\in V^2,x\neq y\right\} }[/math]应为[math]\displaystyle{ E\subseteq\left\{\left\{x,y\right\}:(x,y)\in V^2 \right\} }[/math]。对于无向多重图，[math]\displaystyle{ E\to\left\{\left\{x,y\right\}:(x,y)\in V^2,x\neq y\right\} }[/math]应为[math]\displaystyle{ E\to\left\{\left\{x,y\right\}:(x,y)\in V^2\right\} }[/math]。为避免歧义，这些类型的对象可以分别称为带自环的无向简单图 undirected simple graph permitting loops和带自环的无向多重图 undirected multigraph permitting loops。

（编者注：一种更常见的定义认为简单图是不含重边或自环的图，而多重图是允许重边的图；另外，伪图 pseudograph一说同多重图 multigraph，一说是允许含自环的多重图。）

[math]\displaystyle{ V,E }[/math] 的元素个数通常被认为是有限的；在无限图 infinite graphs中许多著名的性质都会改变或不成立。此外，[math]\displaystyle{ V }[/math] 通常被假定为非空集，而 [math]\displaystyle{ E }[/math] 允许为空集。以下再给出一些图论中的定义：图的阶 order是其顶点个数 [math]\displaystyle{ |V| }[/math]，图的尺寸 size为其边数 [math]\displaystyle{ |E| }[/math]，顶点的度 degree/ valency是关联于该顶点的边的数目（自环会被算两次）。

在[math]\displaystyle{ n }[/math]阶无向简单图中，每个顶点的最大度为 [math]\displaystyle{ n-1 }[/math]，图的最大尺寸为 [math]\displaystyle{ n (n-1) / 2 }[/math]。

带自环无向简单图[math]\displaystyle{ G }[/math]在其顶点上诱导出一个对称齐次关系 homogeneous relation，称为[math]\displaystyle{ G }[/math]的邻接关系 adjacency relation。具体来说，对每条边[math]\displaystyle{ \{ x,y \} }[/math]，端点[math]\displaystyle{ x }[/math]和[math]\displaystyle{ y }[/math]称为彼此邻接 adjacent ，表示为[math]\displaystyle{ x\sim y }[/math]。

有向图

有三个顶点和四条有向边的有向图（双箭头表示双指向）

有向图 directed graph/digraph是边有方向的图。，[5]通常定义为一个有序对 ordered pair [math]\displaystyle{ G=(V,E) }[/math]，其中

  • [math]\displaystyle{ V }[/math] 是顶点 vertices/nodes/points的集合；
  • [math]\displaystyle{ E\subseteq\left\{\left\{x,y\right\}:(x,y)\in V^2,x\neq y\right\} }[/math] 是边 edges/directed edges/directed links/directed lines/arrows/arcs的集合，边由所有顶点的无序对 ordered pair构成（换句话说，边连接了顶点对）。

为避免歧义，上面定义的对象可被更精准地称作有向简单图 directed simple graph。

在从[math]\displaystyle{ x }[/math]指向[math]\displaystyle{ y }[/math]的边[math]\displaystyle{ (x,y) }[/math]中，顶点 x 和 y 称为边的端点 endpoints，[math]\displaystyle{ x }[/math]为边的尾部 tail ，[math]\displaystyle{ y }[/math]为边的头部 head。 边[math]\displaystyle{ (y,x) }[/math]称为[math]\displaystyle{ (x,y) }[/math]的inverted edge。边称为连接 join/incident on[math]\displaystyle{ x }[/math]和[math]\displaystyle{ y }[/math]。 图中的某顶点可能不属于任意一条边。自环 loop是连接顶点与自身的边。重边 Multiple edges是连接同一对顶点的两条或多条边。

允许重边时，上述定义可以推广：有向图是有序三元组 ordered triple [math]\displaystyle{ G=(V,E,\phi) }[/math]，其中

  • [math]\displaystyle{ V }[/math] 是点集；
  • [math]\displaystyle{ E }[/math] 是边集；
  • [math]\displaystyle{ \phi:E\to\left\{\left\{x,y\right\}:(x,y)\in V^2,x\neq y\right\} }[/math] 是一个将每条边映射到一个无序顶点对的关联函数 incidence function（于是边连接了顶点对）。

为避免歧义，上面定义的对象可被更精准地称作有向多重图 directed multigraph。

上述两个定义中的图不能有自环。为了允许自环，需要扩展定义。对于有向简单图，[math]\displaystyle{ E\subseteq\left\{\left\{x,y\right\}:(x,y)\in V^2,x\neq y\right\} }[/math]应为[math]\displaystyle{ E\subseteq\left\{\left\{x,y\right\}:(x,y)\in V^2 \right\} }[/math]。对于有向多重图，[math]\displaystyle{ E\to\left\{\left\{x,y\right\}:(x,y)\in V^2,x\neq y\right\} }[/math]应为[math]\displaystyle{ E\to\left\{\left\{x,y\right\}:(x,y)\in V^2\right\} }[/math]。为避免歧义，这些类型的对象可以分别称为带自环的有向简单图 undirected simple graph permitting loops和带自环的有向多重图 undirected multigraph permitting loops/箭图 quiver。

带自环的有向简单图[math]\displaystyle{ G }[/math]在其顶点上诱导出一个对称齐次关系 homogeneous relation，称为[math]\displaystyle{ G }[/math]的邻接关系 adjacency relation。具体来说，对每条边[math]\displaystyle{ \{ x,y \} }[/math]，端点[math]\displaystyle{ x }[/math]和[math]\displaystyle{ y }[/math]称为彼此邻接 adjacent ，表示为[math]\displaystyle{ x\sim y }[/math]。

应用

2013年夏某月贡献于维基百科不同语言版本（顶点）的编者（边）形成的网络图[6]

图可以用来模拟物理、生物、[7][8] 社会和信息系统中许多类型的关系和过程。许多实际问题可以用图表示。为强调其在现实世界系统中的应用，网络 network这个术语有时被定义为图，其中的属性（例如名称）与顶点和边相关联，而通过网络来理解和表达现实世界系统的学科被称为网络科学 network science。

计算机科学

在计算机科学中，图用于表示通信网络、数据组织、计算设备、计算流程等。例如，网站的链接结构可以用有向图表示，其中顶点表示网页，有向边表示从一个网页到另一个网页的链接。在社交媒体、旅行、生物学、计算机芯片设计、神经退行性 neuro-degenerative疾病的发展图绘等领域也可以采用类似的方法。因此，开发图的相关算法是计算机科学的重要领域。图转换 graph transformation通常用图重写 Graph rewriting系统来表示。图形转换系统侧重于基于规则的内存式图形操作，与之互补的是面向事务安全 transaction-safe、持久 persistent存储和图形结构数据查询的图形数据库 graph-structured data(GDB)。

语言学

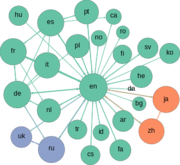
现有研究通过多种途径证明了图论在语言学 linguistics研究中的作用，因为自然语言往往有适合自己的离散结构。传统上，语法 syntax和组合语义 compositional semantics遵循基于树的结构，其表达能力基于复合性原理 principle of compositionality，且是在层次图中建模的。更现代的方法，如中心语驱动词组结构律 head-driven phrase structure grammar(HPSG)，使用类型特征结构 typed feature structures——有向无环图 directed acyclic graphs对自然语言的语法建模。在尤其是应用于计算机的词汇语义学 lexical semantics中，当一个给定词可被相关的词解释时，建立词义模型变得更加容易; 因此，语义网络 semantic networks在计算语言学 computational linguistics中很重要。 不过，音系学 phonology中的其他方法（例如使用格图 lattice graphs的优选论 optimality theory）和形态学 morphology（例如使用有限状态置换器 finite-state transducers的有限状态构词法 finite-state morphology）在将语言作为图形分析时很常见。实际上，数学的这个领域对语言学的用处已经促进了一些组织的出现，如TextGraphs，以及各种各样的“Net”项目，如WordNet、VerbNet VerbNet等。

物理和化学

图论在化学和物理学中也被用来研究分子。在凝聚态物理学 condensed matter physics中，通过收集与原子拓扑结构有关的图论性质的统计数据，可以定量地研究复杂模拟原子结构的三维结构。此外，“费曼图 Feynman diagram和计算规则以一种与人们想要理解的实验数字密切相关的形式总结了量子场论 quantum field theory(QFT)。”在化学中，图为分子建立了一个自然的模型，其中顶点代表原子，边代表键 bonds。这种方法特别适用于分子结构的计算机处理，从分子编辑器 chemical editors到数据库检索。在统计物理学 statistical physics中，图可以表示系统中相互作用的部分之间的局部联系，以及这些系统上物理过程的动态。类似地，在计算神经科学 computational neuroscience中，图可以用来表示大脑区域之间的功能联系，这些区域相互作用产生各种认知过程，顶点代表大脑的不同区域，边代表这些区域之间的联系。图论在电网络的电学建模中起着重要作用，在这里，权值与导线段的电阻联系起来，以获得网络结构的电学特性。图形也用来表示多孔介质 porous media的微尺度通道，其中顶点代表孔隙，边代表连接孔隙的较小通道。化学图论 Chemical graph theory利用分子图 molecular graph来建立分子模型。图形和网络是研究和理解相变 phase transitions和临界现象 critical phenomena的优秀模型。去除节点或边会导致了临界过渡，在此过程中网络分裂成小簇，作为相变研究。分裂过程被用逾渗理论 percolation theory研究。

社会科学

社会学中的图论：莫雷诺社会关系网图 Moreno Sociogram

图论在社会学 sociology中也有广泛应用，例如，通过社会网络分析 social network analysis(SNA)软件来衡量演员的声望或研究谣言的传播。在社交网络领域有许多不同类型的图表。交往关系与友谊网图 Acquaintanceship and friendship graphs描述了人们是否认识彼此。影响图 Influence graphs表示某人是否可以影响他人的行为。 最后，协作图 collaboration graphs表示两个人是否以某种特定的方式一起工作，例如出演同一部电影。

生物学

同样，图论在生物学和保护工作中也很有用，其中一个顶点可以代表某些物种存在（或栖息）的区域，而边则代表迁移路径或区域之间的移动。这些信息对于观察繁殖模式、跟踪疾病或寄生虫的传播及其对其他物种的影响都非常重要。

图论也用于连接组学 connectomics；神经系统可以看作一个图，其中节点是神经元，边是它们之间的连接。

数学

在数学中，图在几何学和拓扑学中纽结理论 knot theory等领域是有用的。代数图论 Algebraic graph theory与群论 group theory有着密切的联系。代数图论已被应用到动态系统和复杂性等许多领域。

其他

通过给图的每条边赋予权重，可以扩展图的结构。具有权重的图，或称加权图 weighted graphs，用于表示成对连接具有某些数值的结构。例如，如果一个图表示一个道路网络，权重可以表示每条道路的长度。 每条边可能有几个相关的权重，包括距离、旅行时间或货币成本。这种加权图通常用于编写GPS和比较航班时间和成本的旅行计划搜索引擎。

历史

柯尼斯堡七桥问题

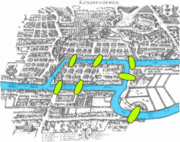
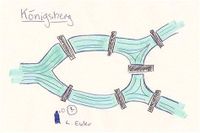
一般认为，欧拉 Leonhard Euler于1736年出版的关于柯尼斯堡七桥问题 Seven Bridges of Königsberg的论文是图论领域的第一篇文章。此问题被推广为著名的欧拉路问题，亦即一笔画问题。而该论文与范德蒙德 Vandermonde的一篇关于骑士周游问题的文章，则是继承了莱布尼茨 Leibniz提出的“位置分析”的方法。欧拉提出的关于凸多边形顶点数、棱数及面数之间的关系的欧拉公式与图论有密切联系，此后又被柯西 Cauchy等人进一步研究推广，成了拓扑学 topology的起源。1857年，哈密顿 Hamilton发明了“环游世界游戏” icosian game，与此相关的则是另一个广为人知的图论问题“哈密顿路径问题”。

西尔维斯特 Sylvester于1878年发表在《自然》上的一篇论文中首次提出“图”这一术语。

欧拉的论文发表后一个多世纪，凯莱 Cayley研究了在微分学中出现的一种数学分析的特殊形式，而这最终将他引向对一种特殊的被称为“树”的图的研究。由于有机化学中有许多树状结构的分子，这些研究对于理论化学有着重要意义，尤其是其中关于具有某一特定性质的图的计数问题。除凯莱的成果外，波利亚 Pólya也于1935至1937年发表了一些成果，1959年，De Bruijn做了一些推广。这些研究成果奠定了图的计数理论的基础。凯莱将他关于树的研究成果与当时有关化合物的研究联系起来，而图论中有一部分术语正是来源于这种将数学与化学相联系的做法。

四色问题 four color problem可谓是图论研究史上最著名也是产生成果最多的问题之一：“是否任何一幅画在平面上的地图都可以用四种颜色染色，使得任意两个相邻的区域不同色？”这一问题由Francis Guthrie于1852年提出，而最早的文字记载则出现在德摩根 De Morgan于1852年写给哈密顿的一封信上。包括凯莱、肯普 Kempe等在内的许多人都曾给出过错误的证明。泰特Peter Guthrie Tait、希伍德 Percy John Heawood、拉姆齐 Ramsey和Hugo Hadwiger对此问题的研究与推广引发了对嵌入具有不同亏格的曲面的图的着色问题的研究。一百多年后，四色问题仍未解决。1969年，Heinrich Heesch发表了一个用计算机解决此问题的方法。1976年，阿佩尔 Kenneth Appel和沃夫冈·哈肯 Wolfgang Haken借助计算机给出了一个证明，此方法按某些性质将所有地图分为1936类并利用计算机一一验证了它们可以用四种颜色染色。但此方法由于过于复杂，在当时未被广泛接受。

1860年之1930年间，若当 Jordan、库拉托夫斯基 Kuratowski和惠特尼 Whitney从之前独立于图论发展的拓扑学中吸取大量内容进入图论，而现代代数方法的使用更让图论与拓扑走上共同发展的道路。其中应用代数较早者如物理学家基尔霍夫 Gustav Kirchhoff于1845年发表的基尔霍夫电路定律 Kirchhoff's circuit laws。

图论中概率方法的引入，尤其是埃尔德什 Erdős和Alfréd Rényi关于随机图连通的渐进概率的研究使得图论产生了新的分支随机图论。

图形绘制

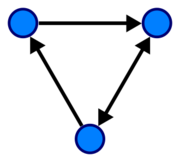
图可以通过为每个顶点画一个点或圆来直观地表示，如果两个顶点由边连接，则在两个顶点之间画一条线。如果图形是有向的，则用箭头表示方向。

图形绘制不应与图形本身（抽象的、非可视化的结构）相混淆，因为有几种方法可以构造图形绘制。重要的是哪些顶点通过多少条边连接到其他顶点，而不是图布局如何。在实践中，通常很难确定两幅图画是否代表同一个图。根据问题所属领域的不同，某些布局可能比其他布局更适合、更容易理解。

杜特 W.T.Tutte的开创性工作对图形绘制学产生了重要影响。此外，他引入了使用线性代数方法绘制图形的方法。

图形绘制包含了处理交叉数 crossing number及其各种推广的问题。图的交叉数是一个图在平面上,边的交叉点的最小数目。对于平面图 planar graph，交叉数按定义为零。

对平面以外的其他表面上的绘图也有相关研究。

图论数据结构

在计算机系统中存储图形有不同的方法。所使用的数据结构取决于图的结构和操作图的算法。理论上可以区分列表结构和矩阵结构，但在具体应用中，最佳结构往往是两者的结合。列表结构往往应用于稀疏图 sparse graphs，因为他们对内存需求较低。而矩阵结构对某些应用访问速度较快，但可能会消耗大量内存。高效稀疏矩阵结构在现代并行计算机体系结构上的实现是当前研究的一个课题。

列表结构包括关联表 incidence list——顶点对数组，及邻接表 adjacency list，它分别列出每个顶点的邻接点: 就像关联表一样，每个顶点都有一个邻接顶点的列表。

矩阵结构包括关联矩阵 incidence matrix——一个由0和1组成的矩阵，其中行代表顶点，列代表边; 及邻接矩阵 adjacency matrix，其中的行和列都按顶点进行索引。在这两种情况下，1表示两个对象相邻，0表示两个对象不相邻。度矩阵 degree matrix表示顶点的度数。拉普拉斯矩阵 Laplacian Matrix是邻接矩阵的一种改进形式，它包含了关于顶点度的信息，并且在一些计算中很有用，例如基尔霍夫 Kirchhoff 关于图的生成树 spanning tree的定理。距离矩阵 distance matrix（如邻接矩阵）的行和列都由顶点索引，但每个单元格内不是0或1而是两个顶点之间最短路径 shortest path的长度。

图论问题

图枚举

图形枚举 graph enumeration是满足特定条件的图的计数问题，相关文献很多。

子图相关问题

子图同构问题 subgraph isomorphism problem：给定两个图[math]\displaystyle{ G }[/math]和[math]\displaystyle{ H }[/math]，问[math]\displaystyle{ G }[/math]中是否存在一个子图与[math]\displaystyle{ H }[/math]同构。这是一个NP完全问题。

  • 哈密顿回路问题可视为一个子图同构问题，即给定一个[math]\displaystyle{ n }[/math]个顶点的图，问是否存在一个子图与具有[math]\displaystyle{ n }[/math]个顶点的圈同构。

一类相关的常见问题要求在给定图中寻找符合某些条件的最大子图，其中有很多是NP完全的，如：

  • 分团问题 clique problem：在给定图中寻找最大的团（NP完全）。

类似地，有些问题要求寻找符合某些条件的最大导出子图 induced subgraphs，如：

  • 最大独立集问题 independent set problem：在给定图中寻找最大的无边的导出子图，亦即独立集 independent set（NP完全）。

平面图判定：判定给定的图是否是平面图

一个尚未解决的与子图相关的猜想，重构猜想 Reconstruction conjecture：一个[math]\displaystyle{ n }[/math]阶图是否能够由其所有[math]\displaystyle{ n-1 }[/math]阶导出子图唯一确定？

染色

图论中的许多问题和定理都与图的着色有关。通常，染色需使任意两个相邻顶点不同色或任意邻接边不同色。有关图染色的著名结果和猜想如下:

  • 四色问题 Four-color theorem
  • 完美图问题 strong perfect graph theorem
  • Erdős–Faber–Lovász 猜想 Erdős–Faber–Lovász conjecture
  • 全染色猜想 Total coloring conjecture
  • 列表染色问题 List coloring conjecture
  • 哈德维格猜想（图论） Hadwiger conjecture (graph theory)

包容与统一

约束建模理论关注由偏序 partial order关联的有向图族。在这些应用中，图是按特异性排序的，这意味着更具体并因此包含更多信息的约束图被更一般的图所包含。 图之间的运算包括计算两个图（如果有的话）之间包容关系的方向，以及计算图的统一性。两个参数图的统一定义为与输入一致（即包含所有信息）的最一般的图（或其计算）（如果存在的话）；有效的统一算法是已知的。

对于严格组合 compositional的约束框架，图的统一是充分可满足性和组合函数。 著名的应用包括定理自动证明 automatic theorem proving和语言结构的精化建模。

路径问题

柯尼斯堡七桥问题：在所有桥都只能走一遍的前提下，如何才能把这个地方所有的桥都走遍？
  • 柯尼斯堡七桥问题 Seven bridges of Königsberg
  • 哈密顿回路问题 Hamiltonian path problem
  • 最小生成树 Minimum spanning tree
  • 中国邮路问题 Chinese postman problem
  • 最短路问题 Shortest path problem
  • 斯坦纳树 Steiner tree
  • 三间小屋问题 Three-cottage problem
  • 旅行商问题 Traveling salesman problem（NP难）

网络流与匹配

在与网络流 network flow概念有关的应用中出现了许多问题，例如：

  • 最大流最小割定理 Max flow min cut theorem
  • 最小费用最大流问题
  • 二分图及任意图上的最大匹配
  • 带权二分图的最大权匹配

可见性问题

  • 博物馆保安问题 Museum guard problem

覆盖问题

图的覆盖问题 Covering problems可能涉及到顶点/子图子集上的各种集合覆盖问题 set cover problem(SCP)。

  • 控制集 Dominating set问题是集合覆盖问题的特例，其中集是封闭邻域 neighborhoods
  • 顶点覆盖问题 Vertex cover problem是集合覆盖问题的特例
  • 初始集合覆盖问题，也称碰集 hitting set，可以描述为超图 hypergraph中的顶点覆盖

分解问题

分解 Decomposition，被定义为对图的边集进行划分（在划分的每个部分的边上有必要的多个顶点），有各类问题。通常，需要将图分解为与给定图同构的子图; 例如，将一个完全图 complete graph分解为哈密顿圈 Hamiltonian cycle。其他问题指定一个图族，其中一个给定的图应该被分解，例如，一个圈族，或将一个完全图[math]\displaystyle{ K_n }[/math]分解为分别分别有[math]\displaystyle{ 1,2,3,...,n-1 }[/math]条边的[math]\displaystyle{ n-1 }[/math]棵指定树。

已经研究的一些具体分解问题包括：

  • 树枝形 Arboricity
  • 双圈覆盖 Cycle double cover
  • 边染色 Edge coloring
  • 图因子分解 Graph factorization

图形类

许多问题涉及到对各类图的成员进行刻画。举例如下：

  • 枚举某类的成员
  • 用禁用子结构 forbidden substructure来描述一个类
  • 确定类之间的关系（例如，图的一个属性是否意味着另一个属性）
  • 寻找有效的算法来决定一个类的成员
  • 查找类成员的表示形式 representation

参见

重要算法

  • 贝尔曼-福特算法 Bellman–Ford algorithm
  • 戴克斯特拉算法 Dijkstra's algorithm (D.A)
  • 克鲁斯卡尔算法 Kruskal's algorithm (K.A)
  • 普里姆算法 Prim's algorithm (P.A)
  • 拓扑排序算法 Topological sorting algorithm (TSA)
  • 关键路径算法 Critical path analysis (CPA)
  • 广度优先搜索算法 Breadth-first search (BFS)
  • 深度优先搜索算法 Depth-first search (DFS)

分支

  • 代数图论 Algebraic graph theory
  • 几何图论 Geometric graph theory
  • 极图论 Extremal graph theory
  • 概率图论 Probabilistic graph theory
  • 拓扑图论 Topological graph theory

数学相关领域

  • 组合数学 Combinatorics
  • 群论 Group theory
  • 纽结理论 Knot theory
  • 拉姆齐理论 Ramsey theory

推广

  • 超图 Hypergraph
  • 抽象单纯复形 Abstract simplicial complex

杰出的图形理论家

  • Alon, Noga
  • Berge, Claude
  • Bollobás, Béla
  • Bondy, Adrian John
  • Brightwell, Graham
  • Chudnovsky, Maria
  • Chung, Fan
  • Dirac, Gabriel Andrew
  • Erdős, Paul
  • Euler, Leonhard
  • Faudree, Ralph
  • Fleischner, Herbert
  • Golumbic, Martin
  • Graham, Ronald
  • Harary, Frank
  • Heawood, Percy John
  • Kotzig, Anton
  • Kőnig, Dénes
  • Lovász, László
  • Murty, U. S. R.
  • Nešetřil, Jaroslav
  • Rényi, Alfréd
  • Ringel, Gerhard
  • Robertson, Neil
  • Seymour, Paul
  • Sudakov, Benny
  • Szemerédi, Endre
  • Thomas, Robin
  • Thomassen, Carsten
  • Turán, Pál
  • Tutte, W. T.
  • Whitney, Hassler

参考文献

  1. ↑ Bender, Edward A.; Williamson, S. Gill (2010). Lists, Decisions and Graphs. With an Introduction to Probability. https://books.google.fr/books?id=vaXv_yhefG8C. p.148
  2. ↑ See, for instance, Iyanaga and Kawada, 69 J, p. 234 or Biggs, p. 4.
  3. ↑ Bender, Edward A.; Williamson, S. Gill (2010). Lists, Decisions and Graphs. With an Introduction to Probability. https://books.google.fr/books?id=vaXv_yhefG8C. p.149
  4. ↑ See, for instance, Graham et al., p. 5.
  5. ↑ Bender, Edward A.; Williamson, S. Gill (2010). Lists, Decisions and Graphs. With an Introduction to Probability. https://books.google.fr/books?id=vaXv_yhefG8C. p.161
  6. ↑ Hale, Scott A. (2013). "Multilinguals and Wikipedia Editing". Proceedings of the 2014 ACM Conference on Web Science - WebSci '14: 99–108. arXiv:1312.0976. Bibcode:2013arXiv1312.0976H. doi:10.1145/2615569.2615684. ISBN 9781450326223.
  7. ↑ Mashaghi, A.; et al. (2004). "Investigation of a protein complex network". European Physical Journal B. 41 (1): 113–121. arXiv:cond-mat/0304207. Bibcode:2004EPJB...41..113M. doi:10.1140/epjb/e2004-00301-0.
  8. ↑ Shah, Preya; Ashourvan, Arian; Mikhail, Fadi; Pines, Adam; Kini, Lohith; Oechsel, Kelly; Das, Sandhitsu R; Stein, Joel M; Shinohara, Russell T (2019-07-01). "Characterizing the role of the structural connectome in seizure dynamics". Brain (in English). 142 (7): 1955–1972. doi:10.1093/brain/awz125. ISSN 0006-8950.

编者推荐

扩展阅读：

本中文词条由Dorr用户参与编译，刘佩佩审校，Meng莫和费米子编辑，欢迎在讨论页面留言。


本词条内容源自wikipedia及公开资料，遵守 CC3.0协议。

取自“https://wiki.swarma.org/index.php?title=图论&oldid=4299”