PageRank算法
PageRank(PR)算法,又称为网页排名算法,Google左侧排算法,由谷歌创始人之一的拉里·佩奇 Larry Page命名。PageRank是一种衡量网站页面重要性的方法。根据谷歌的说法: PageRank通过计算页面链接的数量和质量来粗略估计分析网站的重要性。基本假设是:更重要的页面往往更多地被其他页面引用(或称其他页面中会更多地加入通向该页面的超链接)。
目前该算法不再是谷歌用于排序搜索结果的唯一算法,但它是谷歌公司使用的第一个排序搜索算算法,也是最著名的算法。截止至2019年9月24日,PageRank和所有的相关专利已过期。
描述
PageRank是一种链接分析算法,它通过对超链接集合(如万维网)中的元素实现数值权重赋值,实现“衡量集合范围内某一元素的相关重要性”的目的。该算法可以应用于带有相互引用或者引用关系的任何实体集合。算法赋值给任何给定元素E的数值权重称为E的PageRank,并且用PR(E) 表示。
PageRank的结果来源于一种基于图论的数学算法。它将万维网上所有的网页视作节点 node,而将超链接视作边 edge,并且考虑到了一些权威的网站,类似cnn.com或者qq.com。每个节点的权重值表示对应的页面的重要度。通向该网页的超链接称做“对该网页的投票 a vote of support”。每个网页的权重值大小被递归地定义,依托于所有链接该页面的页面的权重值。例如,一个被很多页面的链接的页面将会拥有较高的权重值。
自Page和谢尔盖·布林 Sergey Brin(Google的另外一位创始人)的原始论文以来,已经发表了许多有关PageRank的学术论文。实际上,PageRank概念可能容易受到利用。相关的研究会关注那些因受到影响而出现错误的PageRank结果,以找到一种有效地避免其PageRank被错误影响的方法(如忽略部分错误的链接)。 PageRank算法中的点击算法是由乔恩·克莱因伯格 Jon Kleinberg提出的。而其他的基于链接的网页排名算法有Kleinberg发明的HITS算法,IBM CLEVER Project,TrustRank算法以及hummingbird算法等等。
历史
Page和Brin于1996年在斯坦福大学开发了PageRank,这是关于一种新型搜索引擎研究项目的一部分。赫克托·加西亚·莫利纳 Hector Garcia-Molina,斯坦福大学计算机科学教授,也是Brin的导师,提供了页面排名算法开发的背景知识。Brin的想法是,可以通过“链接流行度 Link popularity”按层次结构对Web上的信息进行排序:网页的排名越高,链接就越多。该系统是在Scott Hassan和Alan Steremberg的帮助下开发的,Page和Brin都认为他们对Google的发展至关重要。Rajeev Motwani和Terry Winograd与Page和Brin共同撰写了有关该项目的第一篇论文,描述了PageRank和Google搜索引擎的初始原型。此后不久,Page和Brin创立了Google公司,谷歌搜索为其产品。PageRank目前虽然只是决定Google搜索结果排名的众多因素之一,但仍继续为所有Google搜索提供基础。
"PageRank"这个名字里面的"Page"来源于Larry Page,也源于网页 Web Page。但是这项专利为斯坦福大学所有,作为交换,斯坦福大学拥有谷歌的180万股的股份。
PageRank收到引文分析 Citation analysis研究的启发,这是20世纪50年代宾夕法尼亚大学的Eugene Garfield和Hyper Search和University of Padua的Massimo Marchiori。在PageRank被提出的同一年,Jon Kleinberg 发表了HITS的研究成果。HITS也是一种网络重要性分析的算法,按照HITS算法,用户输入关键词后,算法对返回的匹配页面计算两种值,一种是枢纽值 Hub Scores,另一种是权威值 Authority Scores,这两种值是互相依存、互相影响的。所谓枢纽值,指的是页面上所有导出链接指向页面的权威值之和。权威值是指所有导入链接所在的页面中枢纽之和。
算法
PageRank的基本思想
PageRank算法通过输出概率分布来体现某人随机地点击某个链接的概率。PageRank值(PR)可以在任何规模的文件集合中计算得出,而每个链接都指向该集合中的某个特定文件。相关研究论文指出,在初次计算前,总概率将被均分到每个文件上,使得集合中的每个文件被访问的概率都是相同的。接下来在重复多次的计算(又称为“迭代”)中,算法将根据集合的实际情况不断调整PR值,使得其越来越接近最真实的理论值。
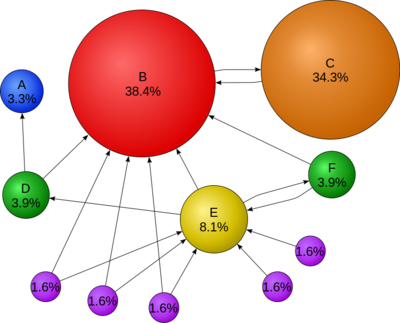
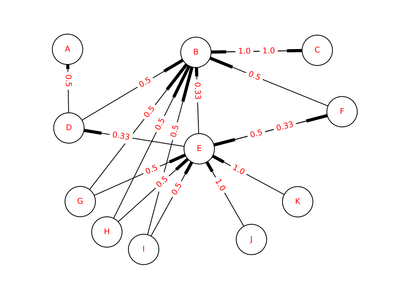
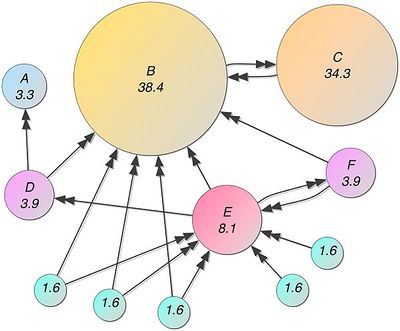
PageRank的设计受到学术论文引用启发。衡量一篇学术论文质量高与否,最重要的一个指标是引用次数,高引用量的论文通常意味着高质量。同理,如果一张网页被引用(以超链接的形式)多了,那么该网页就比较重要。总结起来,PageRank的核心思想有两点(结合图1说明):
越多的网页链接到一个网页(可以理解成投票,D --> B,D给B投了一票),说明这个网页更加重要,如图1的B。(一篇论文被很多论文引用)
PageRank高的网页链接到一个网页,说明这张网页也很重要。如图1,尽管C只有一张网页B链接到它,但C的重要性高于E,尽管E有一堆小罗罗给它投票。(论文被大牛引用了,说明这篇论文很有价值)(也可以从话语权角度理解,重要的人说话份量重)
万维网 World Wide Web可以抽象成一张有向图,节点表示网页,连线[math]\displaystyle{ p_i -\gt p_j }[/math]表示网页[math]\displaystyle{ p_i }[/math]包含了超链接[math]\displaystyle{ p_j(p_i指向了p_j) }[/math]。对图中每个节点的重要性进行量化,则就可以对网页进行排序。PageRank提出之初就是为了对网页进行排序。
搜索引擎的工作原理可以简化为:输入关键词,返回与该关键词相关的网页(一个集合,相当于得到一张子图),在该子图上计算每个节点的PageRank值,PageRank值高的网页排在前面,低的就排在后面。
计算PageRank
计算一个网页的[math]\displaystyle{ p_{i} }[/math]的PR值,则我们需要清楚两个信息:
- 有多少网页链接到了[math]\displaystyle{ p_{i} }[/math]
- 这些网页的PR值
其他网页的PR值很可能是依赖于[math]\displaystyle{ p_{i} }[/math]。这就陷入了一个循环,要想知道[math]\displaystyle{ p_{i} }[/math]的PR值,就得知道链向[math]\displaystyle{ p_{i} }[/math]所有网页的PR值,而要知道其他网页的PR值,又得先知道[math]\displaystyle{ p_{i} }[/math]的PR值。
为了打破这个循环,Page和Brin采用了很巧妙的思路,他们分析一个虚拟用户在互联网上的漫游过程。 他们假定:虚拟用户一旦访问了一个网页,下一步将以相同的概率访问被该网页所链接的任何一个其它网页。比如,网页[math]\displaystyle{ p_i }[/math]包含了[math]\displaystyle{ N }[/math]个超链接,那么虚拟用户访问这[math]\displaystyle{ N }[/math]个页面中的任何一个的概率就是1。那么,网页的排序就可以堪称一个虚拟用户在万维网漫游了很长时间,页面被访问的概率越大,其PR值就越高,网页排名也越靠前。
简化的PageRank的例子
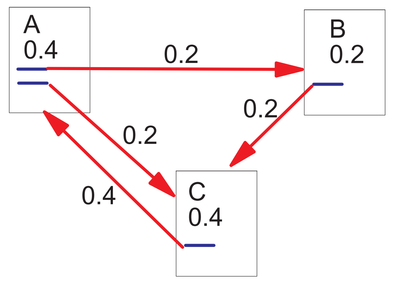
如图2所示,每个节点初始化或者指定一个PageRank值(如[math]\displaystyle{ PR(A)=0.4 }[/math]),网页A包含两个超链接,分别指向B和C(或者说A投票给B和C),[math]\displaystyle{ 0.4 }[/math]拆分成两份,每份[math]\displaystyle{ 0.2 }[/math],所以[math]\displaystyle{ PR(B)=0.2 }[/math]。A和B同时给C投票,所以[math]\displaystyle{ PR(C)=0.2+0.2=0.4 }[/math]。如此,不断地迭代,最后每个节点的值都会收敛,这样就求得了所有节点的PR值。
每个页面将其当前的PageRank值平均分配到本页面所有出链上,一个页面将所有入链的PR值累加起来就构成了该页面新的PR值。如此迭代下去,最后得到一个稳定值。用数学公式表达,如下:
- [math]\displaystyle{ PR(A) = \frac{PR(A)}{L(B)} + \frac{PR(C)}{L(C)} + \frac{PR(D)}{L(D)}+... }[/math]
推广到所有情况,B表示所有链向网页[math]\displaystyle{ p_{i} }[/math]的集合,则:
- [math]\displaystyle{ \sum_{p_{j}\in B(p_{i})} \frac{PR(p_{j)}}{L(p_{j}} }[/math]
但是这样子有存在两个问题:
- 对于没有forward links (outedges)的网页,即只有别人给她投票,她从不给别人投票,那么她的PageRank每次迭代都会增加。
- 对于没有blacklinks (inedges)的网页,即没人给她投票,其PageRank永远等于0。
对于第一个问题,给等式乘以一个小于1的常数[math]\displaystyle{ d }[/math],这个常数被翻译成阻尼系数,意思为任意时刻浏览者访问到某页面后继续访问下一个页面的概率;对于第二个问题,给等式加上一个常数。新的等式如下([math]\displaystyle{ N }[/math]表示网页总数,或者节点数目,本文中该公式成为PageRank基本公式,下同):
- [math]\displaystyle{ PR(p_{i}) = \frac{1-d}{N}+d\sum _{p_{j}\in B(p_{i})}\frac{PR(p_{j}}{L(p_{j}} }[/math]
其中:
- [math]\displaystyle{ B(p_{i}) }[/math]:链接到网页[math]\displaystyle{ p_{i} }[/math]的网页集合。
- [math]\displaystyle{ L(p_{j}) }[/math]:从[math]\displaystyle{ p_{j} }[/math]链出去的网页数目。
这样子,所有的节点的PR值加起来就确保为1了。
简单的实例
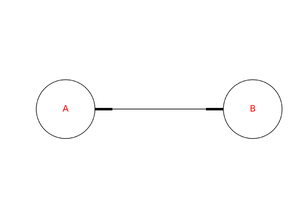
以一个很简单的例子(A < --> B)来看PageRank是怎么收敛的。
假设他们的初始PR值为1,第一次迭代后,[math]\displaystyle{ PR(A) }[/math]和[math]\displaystyle{ PR(B) }[/math]的值为:
PR(A) = 0.15/2 + 0.85*1.0 = 0.9249999999999999
PR(B) = 0.15/2 + 0.85*0.9249999999999999 = 0.8612499999999998
可以得到每次迭代后的值,部分如下:
1: A=0.925000 B=0.861250
2: A=0.807062 B=0.761003
3: A=0.721853 B=0.688575
4: A=0.660289 B=0.636245
5: A=0.615808 B=0.598437
6: A=0.583672 B=0.571121
7: A=0.560453 B=0.551385
8: A=0.543677 B=0.537126
9: A=0.531557 B=0.526823
10: A=0.522800 B=0.519380
11: A=0.516473 B=0.514002
12: A=0.511902 B=0.510116
13: A=0.508599 B=0.507309
14: A=0.506213 B=0.505281
15: A=0.504489 B=0.503815
16: A=0.503243 B=0.502757
17: A=0.502343 B=0.501992
18: A=0.501693 B=0.501439
19: A=0.501223 B=0.501040
20: A=0.500884 B=0.500751
...
42: A=0.500001 B=0.500001
43: A=0.500001 B=0.500000
44: A=0.500000 B=0.500000
45: A=0.500000 B=0.500000
可见,随着迭代次数的增加,PageRank越来越接近收俭值0.5。Python源代码如下:
def pagerank_ab():
"""
Calculate PageRank for A <--> B
"""
pr = {'A':1.0, 'B':1.0}
max_iter = 50
for idx in range(1, max_iter+1):
pr['A'] = 0.15/2 + 0.85*pr['B']
pr['B'] = 0.15/2 + 0.85*pr['A']
s = format(idx, pr['A'],pr['B'])
print(s)
在Python中有一个叫做NetworkX的包可以用于求PageRank。 NetworkX提供3个求PageRank的API,如下:
- pagerank(...)
- pagerank_numpy(...)
- pagerank_scipy(...)
具体细节可见https://networkx.github.io/ 上述例子的完整代码如下:
#!/usr/bin/env python
# -*- coding: utf-8 -*-
import matplotlib.pyplot as plt
import networkx as nx
# Custom packages
import plotnxgraph
def pagerank_ab():
"""
Calculate PageRank for A <--> B
"""
pr = {'A':1.0, 'B':1.0}
max_iter = 50
for idx in range(1, max_iter+1):
pr['A'] = 0.15/2 + 0.85*pr['B']
pr['B'] = 0.15/2 + 0.85*pr['A']
s = format(idx, pr['A'], pr['B'])
print(s)
def plot_graph_pagerank(G, out_file=None):
"""
plot networkx graph whose node label is PageRank
"""
node_and_pr = nx.pagerank(G)
node_size = [pr*20000 for node, pr in node_and_pr.items()]
node_and_labels = {node : node+'\n'+str(round(pr, 3))
for node, pr in node_and_pr.items()}
plotnxgraph.plot_graph(G, out_file=out_file, node_size=node_size,
node_and_labels=node_and_labels, font_size=15)
def main():
# Example 1: A <---> B
# build up a graph
G = nx.DiGraph()
G.add_node('A', pos=(1,0))
G.add_node('B', pos=(2,0))
G.add_path(['A', 'B'])
G.add_path(['B', 'A'])
# pagerank_ab()
plotnxgraph.plot_graph(G, 'simple_example_pagerank_a_b.pdf', node_size=10000, font_size=15)
#node_and_pr = nx.pagerank(G, max_iter=20)
# plot a graph
out_file = 'simple_examples_A_B.pdf'
plot_graph_pagerank(G, out_file)
# Example 2: looping, A --> B --> C --> D --> A
G = nx.DiGraph()
G.add_node('A', pos=(1,1))
G.add_node('B', pos=(2,1))
G.add_node('C', pos=(2,0))
G.add_node('D', pos=(1,0))
G.add_path(['A', 'B', 'C', 'D', 'A'])
out_file = 'simple_examples_loop.pdf'
plot_graph_pagerank(G, out_file)
# Example 3: A --> B --> C <--> A
G = nx.DiGraph()
G.add_node('A', pos=(1,1))
G.add_node('B', pos=(3,1))
G.add_node('C', pos=(2,0))
G.add_path(['A', 'B', 'C', 'A'])
G.add_path(['A', 'C'])
out_file = 'simple_examples_triangle.pdf'
plot_graph_pagerank(G, out_file)
# Example 4: (B, C, D) --> A
G = nx.DiGraph()
G.add_node('B', pos=(1,3))
G.add_node('C', pos=(1,2))
G.add_node('D', pos=(1,1))
G.add_node('A', pos=(2,2))
G.add_path(['B', 'A'])
G.add_path(['C', 'A'])
G.add_path(['D', 'A'])
out_file = 'simple_examples_dangling_node.pdf'
plot_graph_pagerank(G, out_file)
if __name__ == '__main__':
main()
迭代次数
迭代次数越多,结果越准确,但花费时间也越长。出于效率考虑,在实际应用中,当PR值落在误差允许范围内PR值跟前一次比较,如[math]\displaystyle{ PR'(A)-PR(A)\lt 1.0e^{-6} }[/math],其中[math]\displaystyle{ 1.0e^{-6} }[/math]即为浮点数在计算机的存储)就可以返回结果了。Python实现的nx.pagerank相关源代码如下:
# check convergence, l1 norm
err = sum([abs(x[n] - xlast[n]) for n in x])
if err < N*tol: # tol=1.0e-6
return x
在超大型的网络上,会有更加复杂的计算方法,比如分布式计算。
PR 初始值
不管节点PR初始值怎么设置,最后节点的PR值都一样,但收敛不一样。可以修改上面Python代码的PR初始值,运行代码,体验不同的初始值带来的不同效果。NetworkX的pagerank实现是将PR值初始化为[math]\displaystyle{ 1/N }[/math]。
阻尼系数 Damping factor
阻尼系数,公式中记为[math]\displaystyle{ d }[/math],和 PR 初始值一样,d的取值也会影响PageRank算法的效率。在佩奇和布林的论文中,[math]\displaystyle{ d }[/math]通常被设置为[math]\displaystyle{ 0.85 }[/math]。
PageRank的计算方法
迭代法
计算PageRank可以使用迭代法和代数法。两者背后的数学原理是一样的,都遵循PageRank的基本公式,即:
- [math]\displaystyle{ PR(p_{i}) = \frac{1-d}{N}+d\sum _{p_{j}\in B(p_{i})}\frac{PR(p_{j})}{L(p_{j})} }[/math]
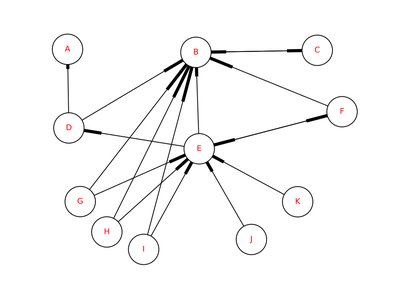
有如下的网页关系:
为了方便讨论和计算,将上图中的节点E下面的节点都标上G,H,I,J,K,如下图所示:
初始化节点PR值
如果没有给节点指定PR初始值,那么每个节点的PR初始化为[math]\displaystyle{ 1/N }[/math]([math]\displaystyle{ N }[/math]为节点数目),下图为例,节点的PR初始值为[math]\displaystyle{ 1/11 }[/math]:
代码如下:
# Step 1: Initiate PageRank
N = G.number_of_nodes() # N = 11
node_and_pr = dict.fromkeys(G, 1.0 / N)
创建随机图 Stochastic graph
随机图是一个有向带权图,边的权重被归一化,使得每个节点的outedges的权重加起来为1。则每个边的权重即为[math]\displaystyle{ 1/L(p_j) }[/math],实例的随机图如下所示:
编写代码时,比如,节点D有两条出链,D --> A和D --> B,所以他们的边权重都是[math]\displaystyle{ 0.5 }[/math]。源代码如下:
stochastic_graph = nx.stochastic_graph(G, weight=weight) # M = 1/L(pj)
print(stochastic_graph['D'])
{'A': {'Edge Id': u'5', 'weight': 0.5}, 'B': {'Edge Id': u'6', 'weight': 0.5}}
迭代计算
遍历所有节点,将每个节点的PR值平均分给其出链的节点,即
- [math]\displaystyle{ \sum_{p_{j}\in B(p_{i})} \frac{PR(p_{j})}{L(p_{j})} }[/math]
乘以阻尼系数[math]\displaystyle{ d }[/math],再加上[math]\displaystyle{ (1−d)/N }[/math]。源代码如下:
dangling_value = (1-d)/N
for _ in range(max_iter): # for each iteration
node_and_prev_pr = node_and_pr
node_and_pr = dict.fromkeys(node_and_prev_pr.keys(), 0)
for node in node_and_pr: # for each node
for out_node in stochastic_graph[node]:
node_and_pr[out_node] += d * node_and_prev_pr[node] * stochastic_graph[node][out_node][weight]
# PR(p_i) = d * PR(p_j)}/L(p_j)
node_and_pr[node] += dangling_value
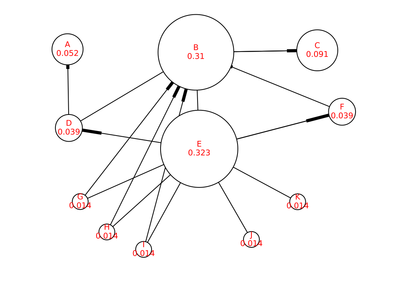
第一次迭代结果如下图所示(有些箭头没显示出来):
当[math]\displaystyle{ PR'(A)-PR(A)\lt 1.0e^{-6} }[/math],即迭代后的PR值跟前一次比较差别很小时,程序的迭代将结束。代码如下:
# check convergence, l1 norm
err = sum([abs(node_and_pr[node] - node_and_prev_pr[node]) for node in node_and_pr])
if err < N*tol:
return node_and_pr
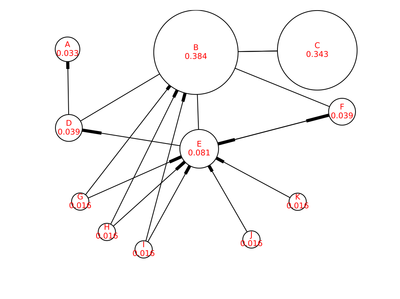
在本例中,需要66次迭代,最后得到的PageRank,如下图:
完整代码:
#!/usr/bin/env python
# -*- coding: utf-8 -*-
import matplotlib.pyplot as plt
import networkx as nx
from networkx.exception import NetworkXError
import numpy as np
import operator
# Custom package
import buildupgraph
import plotnxgraph
def pagerank(G, alpha=0.85, personalization=None,
max_iter=100, tol=1.0e-6, nstart=None, weight='weight',
dangling=None):
if len(G) == 0:
return {}
if not G.is_directed():
D = G.to_directed()
else:
D = G
# Step 1: Create a copy in (right) stochastic form
W = nx.stochastic_graph(D, weight=weight)
N = W.number_of_nodes()
# Plot the stochastic graph
out_file = 'wikipedia_pagerank_example_stochastic_graph.pdf'
edge_and_labels = {k : round(v, 2) for k, v in nx.get_edge_attributes(W, 'weight').items()}
plot_graph(W, out_file=out_file, edge_and_labels=edge_and_labels)
# Step 2: Choose fixed starting vector if not given
if nstart is None:
x = dict.fromkeys(W, 1.0 / N)
else:
# Normalized nstart vector
s = float(sum(nstart.values()))
x = dict((k, v / s) for k, v in nstart.items())
# plot a graph with nstart: starting value of PageRank iteration for each node.
out_file = 'wikipedia_pagerank_example_nstart.pdf'
node_and_labels = {k : k+'\n'+str(round(v, 2))
for k, v in x.items()}
plot_graph(W, out_file=out_file, node_and_labels=node_and_labels)
# Step 3: Assign uniform personalization vector if not given
if personalization is None:
p = dict.fromkeys(W, 1.0 / N)
else:
missing = set(G) - set(personalization)
if missing:
raise NetworkXError('Personalization dictionary '
'must have a value for every node. '
'Missing nodes %s' % missing)
s = float(sum(personalization.values()))
p = dict((k, v / s) for k, v in personalization.items())
# Step 4: Use personalization vector if dangling vector not specified
if dangling is None:
dangling_weights = p
else:
missing = set(G) - set(dangling)
if missing:
raise NetworkXError('Dangling node dictionary '
'must have a value for every node. '
'Missing nodes %s' % missing)
s = float(sum(dangling.values()))
dangling_weights = dict((k, v/s) for k, v in dangling.items())
dangling_nodes = [n for n in W if W.out_degree(n, weight=weight) == 0.0]
# Step 5: power iteration: make up to max_iter iterations
for _ in range(max_iter):
xlast = x
x = dict.fromkeys(xlast.keys(), 0)
danglesum = alpha * sum(xlast[n] for n in dangling_nodes)
for n in x:
# this matrix multiply looks odd because it is
# doing a left multiply x^T=xlast^T*W
for nbr in W[n]:
x[nbr] += alpha * xlast[n] * W[n][nbr][weight] # PR(p_i) = d * PR(p_j)}/L(p_j)
x[n] += danglesum * dangling_weights[n] + (1.0 - alpha) * p[n] # danglesum/N + (1-d)/N
# Plot graph with one iteration
'''
out_file = 'wikipedia_pagerank_example_iteration_1.pdf'
node_and_pr = x
node_size = [pr*30000 for node, pr in node_and_pr.items()]
node_and_labels = {node : node+'\n'+str(round(pr, 3))
for node, pr in node_and_pr.items()}
plot_graph(G, out_file=out_file, node_size=node_size, node_and_labels=node_and_labels)
'''
# check convergence, l1 norm
err = sum([abs(x[n] - xlast[n]) for n in x])
if err < N*tol:
return x
raise NetworkXError('pagerank: power iteration failed to converge in %d iterations.' % max_iter)
def pagerank_iterative(G, d=0.85, max_iter=100, tol=1.0e-6, weight='weight'):
"""
PageRank calculation iteratively
"""
# Step 1: Initiate PageRank
N = G.number_of_nodes() # N = 11
node_and_pr = dict.fromkeys(G, 1.0 / N)
# Step 2: Create a copy in (right) stochastic form
stochastic_graph = nx.stochastic_graph(G, weight=weight) # M = 1/L(pj)
# Step 3: Power iteration: make up to max_iter iterations
dangling_value = (1-d)/N
for _ in range(max_iter): # for each iteration
node_and_prev_pr = node_and_pr
node_and_pr = dict.fromkeys(node_and_prev_pr.keys(), 0)
for node in node_and_pr: # for each node
for out_node in stochastic_graph[node]:
node_and_pr[out_node] += d * node_and_prev_pr[node] * stochastic_graph[node][out_node][weight]
node_and_pr[node] += dangling_value
# Plot graph with one iteration
'''
out_file = 'wikipedia_pagerank_example_iteration_1.pdf'
node_size = [pr*30000 for node, pr in node_and_pr.items()]
node_and_labels = {node : node+'\n'+str(round(pr, 3))
for node, pr in node_and_pr.items()}
plotnxgraph.plot_graph(G, out_file=out_file, node_size=node_size, node_and_labels=node_and_labels)
return
'''
# check convergence, l1 norm
err = sum([abs(node_and_pr[node] - node_and_prev_pr[node]) for node in node_and_pr])
if err < N*tol:
return node_and_pr
raise NetworkXError('pagerank: power iteration failed to converge in {} iterations.'.format(max_iter))
def main():
# Step 1: Build up a graph
'''
G = buildupgraph.build_graph_wikipedia_pagerank_example()
out_file = 'wikipedia_pagerank_example.graphml'
nx.write_graphml(G, out_file)
'''
in_file = 'wikipedia_pagerank_example_layout.graphml' # Visualize the graph with the help of Graphviz
G = buildupgraph.read_graphml_with_position(in_file)
# Step 2: PageRank calculation
node_and_pr = pagerank_iterative(G)
# Normalized PageRank
total_pr = sum(node_and_pr.values()) # 0.843339703286
node_and_pr = {node : pr/total_pr for node, pr in node_and_pr.items()}
# Plot the graph
node_size = [pr*30000 for node, pr in node_and_pr.items()]
node_and_labels = {node : node+'\n'+str(round(pr, 3))
for node, pr in node_and_pr.items()}
plotnxgraph.plot_graph(G, node_size=node_size, node_and_labels=node_and_labels)
if __name__ == '__main__':
main()
利用代数法计算迭代法中的网页集合,同样对E下面的网页进行G,H,I,J,K编号后。根据基本公式,我们可以把所有节点都放在一块进行矩阵计算,可以得到:
- [math]\displaystyle{ \begin{pmatrix} PR(p_1) \\ PR(p_2) \\ \vdots \\ PR(p_N) \end{pmatrix} = \begin{pmatrix} (1-d)/N \\ (1-d)/N \\ \vdots \\ (1-d)/N \end{pmatrix} + d \begin{pmatrix} \ell(p_1,p_1) & \ell(p_1,p_2) & \cdots & \ell(p_1,p_N) \\ \ell(p_2,p_1) & \ddots & & \vdots \\ \vdots & & \ell(p_i,p_j) & & \\ \ell(p_N,p_1) & \cdots & & \ell(p_N,p_N) \end{pmatrix} }[/math]
或者缩写成:
- [math]\displaystyle{ R = \frac{1-d}{N}1+dMR }[/math]
其中,[math]\displaystyle{ \boldsymbol 1 }[/math]为[math]\displaystyle{ N }[/math]维的列向量,所有元素皆为[math]\displaystyle{ 1 }[/math]。在代码中,以图重的网页集合为例,可以表示该列向量为:
N = len(G.nodes()) # N = 11
column_vector = np.ones((N, 1), dtype=np.int)
[[1]
[1]
[1]
[1]
[1]
[1]
[1]
[1]
[1]
[1]
[1]]
邻接函数 Adjacency functionc
邻接函数,[math]\displaystyle{ \zeta(p_{1},p_{2}) }[/math]组成了矩阵[math]\displaystyle{ M }[/math]
- [math]\displaystyle{ M_{ij} = \ell(p_i,p_j) = \begin{Bmatrix} 1/L(p_j) , 如果j链接到i。 \\ 0 , 其他 \end{Bmatrix} }[/math]
[math]\displaystyle{ L(p_j) }[/math]是指从[math]\displaystyle{ p_j }[/math]链出去得网页数目。
这样矩阵每一行乘以[math]\displaystyle{ R }[/math],就得到了新的PR值,比如第二行(图3的节点B)
- [math]\displaystyle{ M_{ij} = \ell(p_2,p_1) \cdot PR(p_2) + \ell(p_2,p_2) \cdot PR(p_2) + \cdots + \ell(p_2,p_N) \cdot PR(p_2) \\ = 0('A') + 0('B') + 1('C') + \frac{1}{2}('D') + \frac{1}{3}('E') + \frac{1}{2}('F') + \frac{1}{2}('G') + \frac{1}{2}('H') + \frac{1}{2}('I') + 0('J') + 0('K') }[/math]
以节点G为例,G给B和E投票,所以B得到[math]\displaystyle{ \frac{1}{2} }[/math]。
矩阵[math]\displaystyle{ M }[/math]每一列加起来都是[math]\displaystyle{ 1 }[/math](值得注意的是,对于没有出链的节点,列加起来等于0,比如图3的节点A),即:
- [math]\displaystyle{ \sum^{N}_{i=1}\imath (p_{i}, p_{j}) = 1 }[/math]
事实上,[math]\displaystyle{ M }[/math]是一个转移矩阵Transition matrix(也叫概率矩阵Probability matrix,马尔可夫矩阵Markov matrix)。因此,PageRank是Eigenvector centrality的一个变体。
矩阵M
[math]\displaystyle{ M }[/math]可以被看成归一化的图邻接矩阵,即: [math]\displaystyle{ \boldsymbol M = (\boldsymbol K^{-1} \boldsymbol A)^{T} }[/math] 其中,A为图的邻接矩阵,按照上面图中的节点关系为例,
# Get adjacency matrix
nodelist = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K'] # sorted(G.nodes())
A = nx.to_numpy_matrix(G, nodelist)
'A' 'B' 'C' 'D' 'E' 'F' 'G' 'H' 'I' 'J' 'K'
[[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 1. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 1. 0. 1. 0. 1. 0. 0. 0. 0. 0.]
[ 0. 1. 0. 0. 1. 0. 0. 0. 0. 0. 0.]
[ 0. 1. 0. 0. 1. 0. 0. 0. 0. 0. 0.]
[ 0. 1. 0. 0. 1. 0. 0. 0. 0. 0. 0.]
[ 0. 1. 0. 0. 1. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0.]]
[math]\displaystyle{ A }[/math]是对角矩阵,对角线上的元素是对应节点的出度。
nodelist = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K'] # sorted(G.nodes())
list_outdegree = map(operator.itemgetter(1), sorted(G.out_degree().items()))
K = np.diag(list_outdegree)
[[0 0 0 0 0 0 0 0 0 0 0]
[0 1 0 0 0 0 0 0 0 0 0]
[0 0 1 0 0 0 0 0 0 0 0]
[0 0 0 2 0 0 0 0 0 0 0]
[0 0 0 0 3 0 0 0 0 0 0]
[0 0 0 0 0 2 0 0 0 0 0]
[0 0 0 0 0 0 2 0 0 0 0]
[0 0 0 0 0 0 0 2 0 0 0]
[0 0 0 0 0 0 0 0 2 0 0]
[0 0 0 0 0 0 0 0 0 1 0]
[0 0 0 0 0 0 0 0 0 0 1]]
[math]\displaystyle{ K }[/math]的逆矩阵[math]\displaystyle{ K^{-1} }[/math]为,
K_inv = np.linalg.pinv(K)
[[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. ]
[ 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. ]
[ 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. ]
[ 0. 0. 0. 0.5 0. 0. 0. 0. 0. 0. 0. ]
[ 0. 0. 0. 0. 0.33 0. 0. 0. 0. 0. 0. ]
[ 0. 0. 0. 0. 0. 0.5 0. 0. 0. 0. 0. ]
[ 0. 0. 0. 0. 0. 0. 0.5 0. 0. 0. 0. ]
[ 0. 0. 0. 0. 0. 0. 0. 0.5 0. 0. 0. ]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0.5 0. 0. ]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0. ]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. ]]
根据公式[math]\displaystyle{ \boldsymbol M = (\boldsymbol K^{-1} \boldsymbol A)^{T} }[/math]就可以求得矩阵M,如下:
M = (K_inv * A).transpose()
[[ 0. 0. 0. 0.5 0. 0. 0. 0. 0. 0. 0. ]
[ 0. 0. 1. 0.5 0.33 0.5 0.5 0.5 0.5 0. 0. ]
[ 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. ]
[ 0. 0. 0. 0. 0.33 0. 0. 0. 0. 0. 0. ]
[ 0. 0. 0. 0. 0. 0.5 0.5 0.5 0.5 1. 1. ]
[ 0. 0. 0. 0. 0.33 0. 0. 0. 0. 0. 0. ]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. ]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. ]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. ]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. ]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. ]]
求解
公式中[math]\displaystyle{ R }[/math]为特征向量 eignevector,根据公式:
- [math]\displaystyle{ R = \frac {1-d}{N}1 + dMR }[/math]
可得:
- [math]\displaystyle{ R = (I - dM)^{-1} \frac{1-d}{N}1 }[/math]
其中I是单位矩阵:
d = 0.85
I = np.identity(N)
R = np.linalg.pinv(I - d*M) * (1-d)/N * column_vector
[[ 0.028]
[ 0.324]
[ 0.289]
[ 0.033]
[ 0.068]
[ 0.033]
[ 0.014]
[ 0.014]
[ 0.014]
[ 0.014]
[ 0.014]]
得到R需要归一化,所有节点的PR加起来才能等于1。
R = R/sum(R) # normalized R, so that page ranks sum to 1.
[[ 0.033]
[ 0.384]
[ 0.343]
[ 0.039]
[ 0.081]
[ 0.039]
[ 0.016]
[ 0.016]
[ 0.016]
[ 0.016]
[ 0.016]]
使用NetworkX作图后得到的结果:
完整代码如下:
#!/usr/bin/env python
# -*- coding: utf-8 -*-
import matplotlib.pyplot as plt
import networkx as nx
from networkx.exception import NetworkXError
import numpy as np
import operator
import fractions
# Custom package
import buildupgraph
def pagerank_numpy(G, alpha=0.85, personalization=None, weight='weight', dangling=None):
"""Return the PageRank of the nodes in the graph.
"""
if len(G) == 0:
return {}
M = nx.google_matrix(G, alpha, personalization=personalization,
weight=weight, dangling=dangling)
# use numpy LAPACK solver
eigenvalues, eigenvectors = np.linalg.eig(M.T)
ind = eigenvalues.argsort()
# eigenvector of largest eigenvalue at ind[-1], normalized
largest = np.array(eigenvectors[:, ind[-1]]).flatten().real
norm = float(largest.sum())
return dict(zip(G, map(float, largest / norm)))
def main():
# Step 1: Build up a graph
'''
G = build_graph_wikipedia_pagerank_example()
out_file = 'wikipedia_pagerank_example.graphml'
nx.write_graphml(G, out_file)
'''
in_file = 'wikipedia_pagerank_example_layout.graphml'
G = buildupgraph.read_graphml_with_position(in_file)
# Step 2: Compute PageRank algebraically
#np.set_printoptions(formatter={'float_kind':lambda x: str(fractions.Fraction(x).limit_denominator())})
np.set_printoptions(precision=2)
# Part 1: \mathbf {1} is the column vector of length N containing only ones.
N = len(G.nodes()) # N = 11
column_vector = np.ones((N, 1), dtype=np.int)
#print(column_vector)
# Part 2: Matrix M
# Adjacency matrix A
nodelist = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K'] # sorted(G.nodes())
A = nx.to_numpy_matrix(G, nodelist)
# K is the diagonal matrix with the outdegrees in the diagonal.
nodelist = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K'] # sorted(G.nodes())
list_outdegree = map(operator.itemgetter(1), sorted(G.out_degree().items()))
K = np.diag(list_outdegree)
K_inv = np.linalg.pinv(K)
# Matrix M
M = (K_inv * A).transpose()
# Part 3: PageRank calculation
np.set_printoptions(precision=3)
d = 0.85
I = np.identity(N)
R = np.linalg.pinv(I - d*M) * ((1-d)/N * column_vector)
R = R/sum(R) # normalized R, so that page ranks sum to 1.
print(R)
return
# Part 4: Using nx.pagerank_numpy
#pr = nx.pagerank_numpy(G)
pr = pagerank_numpy(G)
print(pr)
if __name__ == '__main__':
main()
演化
无向图的PageRank
无向图G的PageRank在统计上接近图G 的度分布,但它们通常是不同的:如果R 是上面定义的PageRank向量,那么 D是度分布向量:
- [math]\displaystyle{ D = {1\over 2|E|} \begin{bmatrix} \deg(p_{1}) \\ \deg(p_{2}) \\ \vdots \\ \deg(p_{N}) \end{bmatrix} }[/math]
其中deg(p_i) 表示顶点p_i的度,而E是图的连边集,Y=1(1/N)表示为:
- [math]\displaystyle{ {1-d\over1+d}\|Y-D\|_1\leq \|R-D\|_1\leq \|Y-D\|_1, }[/math]
也就是说,当且仅当该图是规则的,即每个顶点具有相同的度数时,无向图的PageRank等于度数分布矢量。
针对PageRank的分布式算法
Sarma 等人描述了两种基于随机游走的分布式算法,用于计算网络中节点的 PageRank。 一种算法[math]\displaystyle{ O(\log n/\epsilon) }[/math] 在任何图(有向图或无向图)上以高概率四舍五入,其中[math]\displaystyle{ n }[/math]是网络规模,[math]\displaystyle{ \epsilon }[/math]是重置概率([math]\displaystyle{ 1- \epsilon }[/math]为PageRank计算中使用的阻尼因子)。他们还提出了一种更快的算法[math]\displaystyle{ O(\sqrt{\log n}/\epsilon) }[/math],在无向图中四舍五入。在这两种算法中,每个节点每轮处理并发送网络位数n中多对数的位。
谷歌工具栏
Google工具栏具有PageRank功能,该功能可将访问页面的PageRank显示为介于0到10之间的整数。最受欢迎的网站显示的PageRank为10,浏览可能性最小的页面的PageRank为0。Google并未披露工具栏确定网页PageRank值的具体方法,该值仅被视为网站价值的粗略指示。2016年3月,Google宣布将不再支持此功能。
搜索引擎结果页(SERP)
在搜索引擎结果页面(SERP)是由搜索引擎响应关键词查询返回的实际结果。SERP由带有相关文本片段的网页链接列表组成。网页的SERP等级是指相应链接在SERP上的位置,其中较高的位置表示较高的SERP等级。网页的SERP排名不仅是其PageRank的函数,而且是相对较大且不断调整的一组因素(超过200个)的函数。 搜索引擎优化(SEO)旨在影响网站或一组网页的SERP排名。 网页在Google SERP上某个关键字的位置取决于相关性和声誉,也称为权威性和受欢迎度。PageRank是Google评估其网页信誉的一种指示:它是非关键字特定的。Google使用网页和网站权限的组合来确定竞争关键字的网页的总体权限。网站首页的PageRank是Google为网站授权提供的最佳指示。 在将Google地方信息引入主流有机SERP之后,除PageRank之外,还有许多其他因素会影响企业在本地业务结果中的排名。
操纵PageRank
为了优化搜索引擎的结果,一些公司提供向网站管理员出售高PageRank的链接。由于较高PR页面的链接被认为更有价值,因此它们往往更昂贵。在质量和相关站点的内容页面上购买链接广告以提高访问量并提高网站站长的链接流行度成为一种有效可行的营销策略。因此,Google公司有网站出售高PageRank的链接时,该链接将被拉入黑名单(在计算其他页面的PageRanks时将被忽略)。
社会网络属性
Katja Mayer 认为 PageRank 是一个社交网络,因为它将不同的观点和想法在同一个地方联系起来。 人们到网页排名寻找信息,大量引用其他作者关于这个话题的观点。 这创造了一个具有社交属性的平台,在这里所有的东西都可以被讨论和收集,从而引发人们互动和思考。 在网页排名和使用者之间存在着一种社会关系,因为它不断地适应和变化以适应现代社会的变化。 通过社会计量学查看 PageRank 和个人之间的关系,可以深入了解所产生该关系的原因。
Matteo Pasquinelli认为,PageRank具有社会成分的基础在于注意力经济这一概念。通过注意力节约,可以将价值放在那些能吸引更多人的注意力的产品上,而与随后页面上的结果相比,PageRank顶部的结果获得更多的关注(即更高的注意力)。因此,具有较高PageRank的结果有更大的概率进入人类意识,这会进一步的影响浏览该网页的人的行为。高PageRank网页具有更高的潜力来吸引用户的注意力。因此,这些网页可以获得更多的流量,这也能够让用户为他们的业务进行更多的付费。这些网页的PageRank允许它们被信任,并且能够将这种信任增加更多的业务。
PageRank的其他用途
Pagerank算法适用于任何有关于图或图网络的领域。 因此,PageRank经常用于文献计量学、社会和信息网络分析,以及连边预测和推荐。 它甚至被用于道路网络的系统分析,以及生物学、化学、神经科学和物理学。
学术界
Pagerank被用来量化研究人员的科学影响力。 底层的引用和协作网络与Pagerank算法结合使用,为作者和期刊提供排名。在H指数显示出许多缺点的情况下,被称为pagerank-index(Pi)的新指数被认为是更加公平的计量研究人员科学影响力的方法。 对于生物学中的蛋白质网络分析,PageRank也是有用的工具。 在任何生态系统中,都可以使用PageRank的修改版来确定对环境的可持续发展不可或缺的物种。 网页排名的一个新用途是根据博士学位课程的毕业生担任教职的情况,对其进行排名。 用 PageRank 术语来说,学术部门之间的联系是通过相互雇佣教员来实现的。 一个版本的 PageRank 最近被提议用来取代传统的 ISI 影响因子,并在 Eigenfactor 和 SCImago 实施。 与仅仅计算引文总数不同,每条引文的“重要性”是以 PageRank 的方式确定的。 在神经科学中,已经发现神经网络中神经元的PageRank 与它的相对放电速率相关。
互联网
Twitter使用针对其网站的PageRank向用户推荐他们可能想要关注的账号。 Swiftype 的网站搜索产品通过查看每个网站的重要性信号,并根据主页链接数量等因素对内容进行优先排序,从而建立一个“针对单个网站的 PageRank”。 一个网络爬虫可以使用 PageRank 作为它用来确定在网络爬行过程中访问哪个 URL 的重要度量之一。 创建 Google 时使用的早期工作论文之一是高效地搜索 URL 排序,讨论了一系列不同重要性度量标准的使用,以确定 Google 搜索网站的深度和程度。 网页排名是众多重要性指标中的一个,尽管还有其他一些指标,比如一个 URL 的入站和出站链接的数量,以及站点的根目录到 URL 的距离。 Pagerank 也可以作为一种方法来衡量像 Blogosphere 这样的社区对整个 Web 本身的影响。 因此,这种方法使用 PageRank 来衡量注意力的分布情况,这种分布情况反映了无标度网络模式。
其他
2005年,在巴基斯坦进行的一项试点研究中,“结构性深层民主 Structural Deep Democracy(SD2)”被用于一个名为“Contact Youth”的可持续农业组织的领导层的选举。SD2使用PageRank来处理传递式代理投票,另外还有每个投票者至少要委托两个初始代理的约束,所有选民都是代理候选人。可以在SD2的基础上构建更复杂的变体,例如添加专家代理和针对特定问题的直接投票,但是作为基础的总体系统,SD2要求总是使用通用代理。 在体育运动中,PageRank 算法被用来对球队或者运动员的表现进行排名: 美国国家橄榄球联盟(NFL)的球队; 个人足球运动员; 钻石联盟的运动员。 Pagerank 被用于对空间或街道进行排序,以预测有多少人(行人或车辆)来到各个空间或街道。 在词汇语义学中,它被用来进行词义消歧,语义相似度,以及根据词网同义词具有给定的语义属性(如积极性或消极性)的强度自动对它们进行排序。
参考
- Page, L., Brin, S., Motwani, R., & Winograd, T. (1999). The PageRank citation ranking: Bringing order to the web. Stanford InfoLab.
编者推荐
集智学园官网上有关于PageRank与目前图网络结合的课程如何将PageRank算法扩展到图神经网络上
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。