量子计算

此词条暂由彩云小译翻译，未经人工整理和审校，带来阅读不便，请见谅。

文件:Quantum Computer Zurich.jpg

Quantum computer based on superconducting qubits developed by IBM Research in Zürich, Switzerland. The qubits in the device shown here will be cooled to under 1 kelvin using a dilution refrigerator.

qubits developed by IBM Research in Zürich, Switzerland. The qubits in the device shown here will be cooled to under 1 kelvin using a dilution refrigerator.]]

位于苏黎世的 IBM 研究所开发的量子位。这里显示的装置中的量子位将用稀释制冷机冷却到1开尔文以下。]

Quantum computing is the use of quantum-mechanical phenomena such as superposition and entanglement to perform computation. Computers that perform quantum computation are known as quantum computers. Quantum computers are believed to be able to solve certain computational problems, such as integer factorization (which underlies RSA encryption), significantly faster than classical computers. The study of quantum computing is a subfield of quantum information science.

Quantum computing is the use of quantum-mechanical phenomena such as superposition and entanglement to perform computation. Computers that perform quantum computation are known as quantum computers. Quantum computers are believed to be able to solve certain computational problems, such as integer factorization (which underlies RSA encryption), significantly faster than classical computers. The study of quantum computing is a subfield of quantum information science.

量子计算是利用量子力学现象，如叠加和纠缠来执行计算。执行量子计算的计算机被称为量子计算机。量子计算机被认为能够解决某些计算问题，比如 RSA 加密的基础整数分解，比传统计算机要快得多。量子计算是量子信息科学的一个分支。

! -- 历史 --

Quantum computing began in the early 1980s, when physicist Paul Benioff proposed a quantum mechanical model of the Turing machine. Richard Feynman and Yuri Manin later suggested that a quantum computer had the potential to simulate things that a classical computer could not. In 1994, Peter Shor developed a quantum algorithm for factoring integers that had the potential to decrypt RSA-encrypted communications. Despite ongoing experimental progress since the late 1990s, most researchers believe that "fault-tolerant quantum computing [is] still a rather distant dream". In recent years, investment into quantum computing research has increased in both the public and private sector. On 23 October 2019, Google AI, in partnership with the U.S. National Aeronautics and Space Administration (NASA), published a paper in which they claimed to have achieved quantum supremacy. While some have disputed this claim, it is still a significant milestone in the history of quantum computing.

Quantum computing began in the early 1980s, when physicist Paul Benioff proposed a quantum mechanical model of the Turing machine. Richard Feynman and Yuri Manin later suggested that a quantum computer had the potential to simulate things that a classical computer could not. In 1994, Peter Shor developed a quantum algorithm for factoring integers that had the potential to decrypt RSA-encrypted communications. Despite ongoing experimental progress since the late 1990s, most researchers believe that "fault-tolerant quantum computing [is] still a rather distant dream". In recent years, investment into quantum computing research has increased in both the public and private sector. On 23 October 2019, Google AI, in partnership with the U.S. National Aeronautics and Space Administration (NASA), published a paper in which they claimed to have achieved quantum supremacy. While some have disputed this claim, it is still a significant milestone in the history of quantum computing.

量子计算始于20世纪80年代早期，当时物理学家保罗 · 贝尼奥夫提出了图灵机的量子力学模型。 理查德 · 费曼和尤里 · 曼宁后来提出，量子计算机具有模拟传统计算机无法模拟的事物的潜力。1994年，Peter Shor 开发了一种量子算法，用于分解整数，这种算法有可能解密 rsa 加密的通信。尽管自20世纪90年代后期以来实验取得了进展，但大多数研究人员认为“容错量子计算仍然是一个相当遥远的梦想”。近年来，量子计算研究的投资在公共和私营部门都有所增加。2019年10月23日，谷歌人工智能与美国美国国家航空航天局航天局合作发表了一篇论文，声称已经取得了量子优势。虽然有些人对这种说法提出了质疑，但它仍然是量子计算历史上的一个重要里程碑。

! -- 量子计算的基本原理 --

There are several models of quantum computing, including the quantum circuit model, quantum Turing machine, adiabatic quantum computer, one-way quantum computer, and various quantum cellular automata. The most widely used model is the quantum circuit. Quantum circuits are based on the quantum bit, or "qubit", which is somewhat analogous to the bit in classical computation. Qubits can be in a 1 or 0 quantum state, or they can be in a superposition of the 1 and 0 states. However, when qubits are measured the result is always either a 0 or a 1; the probabilities of these two outcomes depend on the quantum state that they were in immediately prior to the measurement. Computation is performed by manipulating qubits with quantum logic gates, which are somewhat analogous to classical logic gates.

There are several models of quantum computing, including the quantum circuit model, quantum Turing machine, adiabatic quantum computer, one-way quantum computer, and various quantum cellular automata. The most widely used model is the quantum circuit. Quantum circuits are based on the quantum bit, or "qubit", which is somewhat analogous to the bit in classical computation. Qubits can be in a 1 or 0 quantum state, or they can be in a superposition of the 1 and 0 states. However, when qubits are measured the result is always either a 0 or a 1; the probabilities of these two outcomes depend on the quantum state that they were in immediately prior to the measurement. Computation is performed by manipulating qubits with quantum logic gates, which are somewhat analogous to classical logic gates.

量子计算有几种模型，包括量子电路模型、量子图灵机、绝热量子计算机、单向量子计算机和各种量子细胞自动机。使用最广泛的模型是量子电路。量子电路是基于量子比特或“量子比特”的，它在某种程度上类似于经典计算中的比特。量子比特可以处于1或0的量子态，也可以处于1和0的叠加态。然而，当量子位被测量时，结果总是要么是0，要么是1; 这两个结果的概率取决于它们在测量之前所处的量子状态。计算是通过量子逻辑门操纵量子位来完成的，这在某种程度上类似于经典逻辑门。

! -- 物理实现 --

There are currently two main approaches to physically implementing a quantum computer: analog and digital. Analog approaches are further divided into quantum simulation, quantum annealing, and adiabatic quantum computation. Digital quantum computers use quantum logic gates to do computation. Both approaches use quantum bits or qubits. There are currently a number of significant obstacles in the way of constructing useful quantum computers. In particular, it is difficult to maintain the quantum states of qubits as they are prone to quantum decoherence, and quantum computers require significant error correction as they are far more prone to errors than classical computers.

There are currently two main approaches to physically implementing a quantum computer: analog and digital. Analog approaches are further divided into quantum simulation, quantum annealing, and adiabatic quantum computation. Digital quantum computers use quantum logic gates to do computation. Both approaches use quantum bits or qubits.

目前实现量子计算机主要有两种方法: 模拟和数字。模拟方法进一步分为量子模拟、量子退火模拟和绝热量子计算。数字量子计算机使用量子逻辑门进行计算。两种方法都使用量子位或量子位。

! -- 可计算性和复杂性 --

Any computational problem that can be solved by a classical computer can also, in principle, be solved by a quantum computer. Conversely, quantum computers obey the Church–Turing thesis; that is, any computational problem that can be solved by a quantum computer can also be solved by a classical computer. While this means that quantum computers provide no additional power over classical computers in terms of computability, they do in theory provide additional power when it comes to the time complexity of solving certain problems. Notably, quantum computers are believed to be able to quickly solve certain problems that no classical computer could solve in any feasible amount of time—a feat known as "quantum supremacy". The study of the computational complexity of problems with respect to quantum computers is known as quantum complexity theory.

Any computational problem that can be solved by a classical computer can also, in principle, be solved by a quantum computer. Conversely, quantum computers obey the Church–Turing thesis; that is, any computational problem that can be solved by a quantum computer can also be solved by a classical computer. While this means that quantum computers provide no additional power over classical computers in terms of computability, they do in theory provide additional power when it comes to the time complexity of solving certain problems. Notably, quantum computers are believed to be able to quickly solve certain problems that no classical computer could solve in any feasible amount of time—a feat known as "quantum supremacy". The study of the computational complexity of problems with respect to quantum computers is known as quantum complexity theory.

原则上，任何可以由经典计算机解决的计算问题问题也可以由量子计算机解决。相反，量子计算机遵循 Church-Turing 理论; 也就是说，任何可以由量子计算机解决的计算问题问题也可以由经典计算机解决。虽然这意味着量子计算机在可计算性方面不能比传统计算机提供额外的能力，但在解决某些问题的时间复杂性方面，理论上它们确实提供了额外的能力。值得注意的是，人们相信，量子计算机能够快速解决某些问题，而任何传统计算机都无法在任何可行的时间内解决这些问题——这一壮举被称为“量子优势”。研究与量子计算机有关的问题的计算复杂性被称为量子复杂性理论。

Quantum operations

量子操作

The Bloch sphere is a representation of a qubit, the fundamental building block of quantum computers.

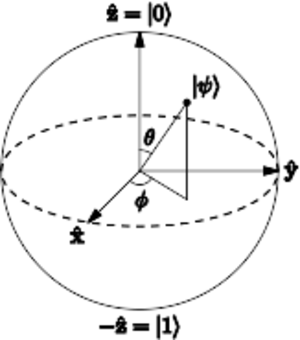
The Bloch sphere is a representation of a qubit, the fundamental building block of quantum computers.

布洛赫球体是量子计算机的基本构件——量子比特的表示。]

The prevailing model of quantum computation describes the computation in terms of a network of quantum logic gates.

The prevailing model of quantum computation describes the computation in terms of a network of quantum logic gates.

流行的量子计算模型用量子逻辑门网络来描述计算。

A memory consisting of [math]\displaystyle{ n }[/math] bits of information has [math]\displaystyle{ 2^n }[/math] possible states. A vector representing all memory states thus has [math]\displaystyle{ 2^n }[/math] entries (one for each state). This vector is viewed as a probability vector and represents the fact that the memory is to be found in a particular state.

A memory consisting of [math]\displaystyle{ n }[/math] bits of information has [math]\displaystyle{ 2^n }[/math] possible states. A vector representing all memory states thus has [math]\displaystyle{ 2^n }[/math] entries (one for each state). This vector is viewed as a probability vector and represents the fact that the memory is to be found in a particular state.

一个包含数学显示"内联"n / 数学位信息的内存有数学显示"内联"2 ^ n / 数学可能的状态。一个代表所有内存状态的向量因此具有 math display"inline"2 ^ n / math entry (每个状态一个)。这个向量被看作是一个概率向量，它表示存储器处于特定状态的事实。

In the classical view, one entry would have a value of 1 (i.e. a 100% probability of being in this state) and all other entries would be zero.

In the classical view, one entry would have a value of 1 (i.e. a 100% probability of being in this state) and all other entries would be zero.

在经典的观点中，一个条目的值为1(即。100% 的概率处于这种状态) ，所有其他条目都是零。

In quantum mechanics, probability vectors are generalized to density operators. This is the technically rigorous mathematical foundation for quantum logic gates, but the intermediate quantum state vector formalism is usually introduced first because it is conceptually simpler. This article focuses on the quantum state vector formalism for simplicity.

In quantum mechanics, probability vectors are generalized to density operators. This is the technically rigorous mathematical foundation for quantum logic gates, but the intermediate quantum state vector formalism is usually introduced first because it is conceptually simpler. This article focuses on the quantum state vector formalism for simplicity.

在量子力学中，概率向量被推广到密度算子。这是量子逻辑门严格技术上的数学基础，但中间量子态向量形式通常是首先介绍，因为它在概念上更简单。为了简单起见，本文着重讨论量子态向量形式。

We begin by considering a simple memory consisting of only one bit. This memory may be found in one of two states: the zero state or the one state. We may represent the state of this memory using Dirac notation so that

We begin by considering a simple memory consisting of only one bit. This memory may be found in one of two states: the zero state or the one state. We may represent the state of this memory using Dirac notation so that

我们首先考虑一个只包含一位的简单内存。这种记忆可以在两种状态之一中找到: 零状态或一种状态。我们可以用狄拉克符号来表示这段记忆的状态

[math]\displaystyle{ \lt math display="block"\gt 数学显示”拦截” |0\rangle := \begin{pmatrix} 1 \\ 0 \end{pmatrix};\quad |0\rangle := \begin{pmatrix} 1 \\ 0 \end{pmatrix};\quad | 0 rangle: begin { pmatrix }10 end { pmatrix } ; quad |1\rangle := \begin{pmatrix} 0 \\ 1 \end{pmatrix} |1\rangle := \begin{pmatrix} 0 \\ 1 \end{pmatrix} | 1 rangle: begin { pmatrix }01 end { pmatrix } }[/math]

</math>

数学

A quantum memory may then be found in any quantum superposition [math]\displaystyle{ |\psi\rangle }[/math] of the two classical states [math]\displaystyle{ |0\rangle }[/math] and [math]\displaystyle{ |1\rangle }[/math]:

A quantum memory may then be found in any quantum superposition [math]\displaystyle{ |\psi\rangle }[/math] of the two classical states [math]\displaystyle{ |0\rangle }[/math] and [math]\displaystyle{ |1\rangle }[/math]:

一个量子内存可能在任何态叠加原理数学显示器“ inline | psi rangle / math of the two classical states math display"inline | 0 rangle / math"inline | 1 rangle / math":

[math]\displaystyle{ \lt math display="block"\gt 数学显示”拦截” |\psi\rangle := \alpha\,|0\rangle + \beta\,|1\rangle |\psi\rangle := \alpha\,|0\rangle + \beta\,|1\rangle | psi rangle: alpha ，| 0 rangle + beta ，| 1 rangle = \begin{pmatrix} \alpha \\ \beta \end{pmatrix};\quad = \begin{pmatrix} \alpha \\ \beta \end{pmatrix};\quad 开始{ pmatrix } alpha beta end { pmatrix } ; quad |\alpha|^2 + |\beta|^2 = 1. |\alpha|^2 + |\beta|^2 = 1. | alpha | ^ 2 + | beta | ^ 21. }[/math]

</math>

数学

In general, the coefficients [math]\displaystyle{ \alpha }[/math] and [math]\displaystyle{ \beta }[/math] are complex numbers. In this scenario, one qubit of information is said to be encoded into the quantum memory. The state [math]\displaystyle{ |\psi\rangle }[/math] is not itself a probability vector but can be connected with a probability vector via a measurement operation. If the quantum memory is measured to determine if the state is [math]\displaystyle{ |0\rangle }[/math] or [math]\displaystyle{ |1\rangle }[/math] (this is known as a computational basis measurement), the zero state would be observed with probability [math]\displaystyle{ |\alpha|^2 }[/math] and the one state with probability [math]\displaystyle{ |\beta|^2 }[/math]. The numbers [math]\displaystyle{ \alpha }[/math] and [math]\displaystyle{ \beta }[/math] are called quantum amplitudes.

In general, the coefficients [math]\displaystyle{ \alpha }[/math] and [math]\displaystyle{ \beta }[/math] are complex numbers. In this scenario, one qubit of information is said to be encoded into the quantum memory. The state [math]\displaystyle{ |\psi\rangle }[/math] is not itself a probability vector but can be connected with a probability vector via a measurement operation. If the quantum memory is measured to determine if the state is [math]\displaystyle{ |0\rangle }[/math] or [math]\displaystyle{ |1\rangle }[/math] (this is known as a computational basis measurement), the zero state would be observed with probability [math]\displaystyle{ |\alpha|^2 }[/math] and the one state with probability [math]\displaystyle{ |\beta|^2 }[/math]. The numbers [math]\displaystyle{ \alpha }[/math] and [math]\displaystyle{ \beta }[/math] are called quantum amplitudes.

一般来说，系数数学显示“ inline" alpha / math”和“ inline" beta / math”都是复数。在这种情况下，一个量子位的信息被称为被编码到量子存储器中。状态数学显示“ inline” | psi rangle / math 本身不是一个概率向量，但可以通过一个测量操作与一个概率向量相连。如果量子内存被测量以确定这个状态是否是数学显示“ inline” | 0 rangle / math 或数学显示“ inline” | 1 rangle / math (这被称为计算基础测量) ，那么零状态将被观察到概率数学显示“ inline” | alpha | ^ 2 / math 和概率数学显示“一个状态” inline | beta | ^ 2 / math。数字数学显示“ inline" alpha / math and math display"inline" beta / math 被称为量子振幅。

The state of this one-qubit quantum memory can be manipulated by applying quantum logic gates, analogous to how classical memory can be manipulated with classical logic gates. One important gate for both classical and quantum computation is the NOT gate, which can be represented by a matrix

The state of this one-qubit quantum memory can be manipulated by applying quantum logic gates, analogous to how classical memory can be manipulated with classical logic gates. One important gate for both classical and quantum computation is the NOT gate, which can be represented by a matrix

这种单比特量子存储器的状态可以通过量子逻辑门来控制，类似于用经典逻辑门来控制经典存储器。经典和量子计算的一个重要门是非门，它可以用矩阵表示

[math]\displaystyle{ X := \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}. }[/math]

[math]\displaystyle{ X := \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}. }[/math]

数学显示“ block” x: begin { pmatrix }0 & 1 & 0{ pmatrix } / math

Mathematically, the application of such a logic gate to a quantum state vector is modelled with matrix multiplication. Thus [math]\displaystyle{ X|0\rangle = |1\rangle }[/math] and [math]\displaystyle{ X|1\rangle = |0\rangle }[/math].

Mathematically, the application of such a logic gate to a quantum state vector is modelled with matrix multiplication. Thus [math]\displaystyle{ X|0\rangle = |1\rangle }[/math] and [math]\displaystyle{ X|1\rangle = |0\rangle }[/math].

在数学上，这种逻辑门应用于量子态矢量是用矩阵乘法来模拟的。因此，数学显示“ inline” x | 0 rangle | 1 rangle / math and math display“ inline x | 1 rangle | 0 rangle / math。

The mathematics of single qubit gates can be extended to operate on multiqubit quantum memories in two important ways. One way is simply to select a qubit and apply that gate to the target qubit whilst leaving the remainder of the memory unaffected. Another way is to apply the gate to its target only if another part of the memory is in a desired state. These two choices can be illustrated using another example. The possible states of a two-qubit quantum memory are

The mathematics of single qubit gates can be extended to operate on multiqubit quantum memories in two important ways. One way is simply to select a qubit and apply that gate to the target qubit whilst leaving the remainder of the memory unaffected. Another way is to apply the gate to its target only if another part of the memory is in a desired state. These two choices can be illustrated using another example. The possible states of a two-qubit quantum memory are

单个量子比特门的数学可以通过两种重要的方式扩展到对多量子比特量子存储器的操作。一种方法是简单地选择一个量子位并将该门应用于目标量子位，同时不影响内存的其余部分。另一种方法是，只有当内存的另一部分处于所需状态时，才将门应用于目标。这两种选择可以用另一个例子来说明。两比特量子存储器的可能状态是

[math]\displaystyle{ \lt math display="block"\gt 数学显示”拦截” |00\rangle := \begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \end{pmatrix};\quad |00\rangle := \begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \end{pmatrix};\quad | 00 rangle: begin { pmatrix }10 end { pmatrix } ; quad |01\rangle := \begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \end{pmatrix};\quad |01\rangle := \begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \end{pmatrix};\quad | 01 rangle: begin { pmatrix }00 end { pmatrix } ; quad |10\rangle := \begin{pmatrix} 0 \\ 0 \\ 1 \\ 0 \end{pmatrix};\quad |10\rangle := \begin{pmatrix} 0 \\ 0 \\ 1 \\ 0 \end{pmatrix};\quad | 10 rangle: begin { pmatrix }010 end { pmatrix } ; quad |11\rangle := \begin{pmatrix} 0 \\ 0 \\ 0 \\ 1 \end{pmatrix}. |11\rangle := \begin{pmatrix} 0 \\ 0 \\ 0 \\ 1 \end{pmatrix}. | 11 rangle: begin { pmatrix }001 end { pmatrix }. }[/math]

</math>

数学

The CNOT gate can then be represented using the following matrix:

The CNOT gate can then be represented using the following matrix:

然后，CNOT 门可以用以下矩阵表示:

[math]\displaystyle{ \lt math display="block"\gt 数学显示”拦截” CNOT := CNOT := 返回文章页面 CNOT: \begin{pmatrix} \begin{pmatrix} 开始{ pmatrix } 1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 0 & 0 & 1 & 0 0 & 0 & 1 & 0 \end{pmatrix}. \end{pmatrix}. End { pmatrix }. }[/math]

</math>

数学

As a mathematical consequence of this definition, [math]\displaystyle{ CNOT|00\rangle = |00\rangle }[/math], [math]\displaystyle{ CNOT|01\rangle = |01\rangle }[/math], [math]\displaystyle{ CNOT|10\rangle = |11\rangle }[/math], and [math]\displaystyle{ CNOT|11\rangle = |10\rangle }[/math]. In other words, the CNOT applies a NOT gate ([math]\displaystyle{ X }[/math] from before) to the second qubit if and only if the first qubit is in the state [math]\displaystyle{ |1\rangle }[/math]. If the first qubit is [math]\displaystyle{ |0\rangle }[/math], nothing is done to either qubit.

As a mathematical consequence of this definition, [math]\displaystyle{ CNOT|00\rangle = |00\rangle }[/math], [math]\displaystyle{ CNOT|01\rangle = |01\rangle }[/math], [math]\displaystyle{ CNOT|10\rangle = |11\rangle }[/math], and [math]\displaystyle{ CNOT|11\rangle = |10\rangle }[/math]. In other words, the CNOT applies a NOT gate ([math]\displaystyle{ X }[/math] from before) to the second qubit if and only if the first qubit is in the state [math]\displaystyle{ |1\rangle }[/math]. If the first qubit is [math]\displaystyle{ |0\rangle }[/math], nothing is done to either qubit.

作为这个定义的数学推论，数学显示"inline CNOT | 00 rangle | 00 rangle / math，math display"inline CNOT | 01 rangle | 01 rangle / math，math display"inline CNOT | 10 rangle | 11 rangle / math，and math display"11 rangle | 10 rangle / math。换句话说，CNOT 对第二个量子位应用 NOT gate (math display"inline"x / math from before) ，当且仅当第一个量子位在状态数学显示""| 1 rangle / math。如果第一个量子位是 math display"inline | 0 rangle / math，那么任何一个量子位都不会被处理。

In summary, a quantum computation can be described as a network of quantum logic gates and measurements. Any measurement can be deferred to the end of a quantum computation, though this deferment may come at a computational cost. Because of this possibility of deferring a measurement, most quantum circuits depict a network consisting only of quantum logic gates and no measurements. More information can be found in the following articles: universal quantum computer, Shor's algorithm, Grover's algorithm, Deutsch–Jozsa algorithm, amplitude amplification, quantum Fourier transform, quantum gate, quantum adiabatic algorithm and quantum error correction.

In summary, a quantum computation can be described as a network of quantum logic gates and measurements. Any measurement can be deferred to the end of a quantum computation, though this deferment may come at a computational cost. Because of this possibility of deferring a measurement, most quantum circuits depict a network consisting only of quantum logic gates and no measurements. More information can be found in the following articles: universal quantum computer, Shor's algorithm, Grover's algorithm, Deutsch–Jozsa algorithm, amplitude amplification, quantum Fourier transform, quantum gate, quantum adiabatic algorithm and quantum error correction.

总之，量子计算可以描述为一个由量子逻辑门和测量组成的网络。任何测量都可以推迟到量子计算结束时进行，尽管这种推迟可能会带来计算成本。由于这种延迟测量的可能性，大多数量子电路描述的网络只有量子逻辑门而没有测量。更多信息可以在以下文章中找到: 通用量子计算机，Shor 算法，Grover 算法，Deutsch-Jozsa 算法，振幅放大，量子傅里叶变换，量子门，量子绝热算法和量子误差修正。

Any quantum computation can be represented as a network of quantum logic gates from a fairly small family of gates. A choice of gate family that enables this construction is known as a universal gate set. One common such set includes all single-qubit gates as well as the CNOT gate from above. This means any quantum computation can be performed by executing a sequence of single-qubit gates together with CNOT gates. Though this gate set is infinite, it can be replaced with a finite gate set by appealing to the Solovay-Kitaev theorem.

Any quantum computation can be represented as a network of quantum logic gates from a fairly small family of gates. A choice of gate family that enables this construction is known as a universal gate set. One common such set includes all single-qubit gates as well as the CNOT gate from above. This means any quantum computation can be performed by executing a sequence of single-qubit gates together with CNOT gates. Though this gate set is infinite, it can be replaced with a finite gate set by appealing to the Solovay-Kitaev theorem.

任何量子计算都可以表示为一个由相当小的量子逻辑门组成的网络。使这种结构成为可能的门系列的选择被称为通用门系列。一个常见的这样的集合包括所有的单量子比特门以及上面的 CNOT 门。这意味着任何量子计算都可以通过执行一系列带有 CNOT 门的单量子比特门来完成。虽然这个门集合是无限的，但是它可以通过引用 Solovay-Kitaev 定理用一个有限的门集合来代替。

Potential applications

潜在的应用

Cryptography

密码学

Main article: Quantum cryptography

Integer factorization, which underpins the security of public key cryptographic systems, is believed to be computationally infeasible with an ordinary computer for large integers if they are the product of few prime numbers (e.g., products of two 300-digit primes). By comparison, a quantum computer could efficiently solve this problem using Shor's algorithm to find its factors. This ability would allow a quantum computer to break many of the cryptographic systems in use today, in the sense that there would be a polynomial time (in the number of digits of the integer) algorithm for solving the problem. In particular, most of the popular public key ciphers are based on the difficulty of factoring integers or the discrete logarithm problem, both of which can be solved by Shor's algorithm. In particular, the RSA, Diffie–Hellman, and elliptic curve Diffie–Hellman algorithms could be broken. These are used to protect secure Web pages, encrypted email, and many other types of data. Breaking these would have significant ramifications for electronic privacy and security.

Integer factorization, which underpins the security of public key cryptographic systems, is believed to be computationally infeasible with an ordinary computer for large integers if they are the product of few prime numbers (e.g., products of two 300-digit primes). By comparison, a quantum computer could efficiently solve this problem using Shor's algorithm to find its factors. This ability would allow a quantum computer to break many of the cryptographic systems in use today, in the sense that there would be a polynomial time (in the number of digits of the integer) algorithm for solving the problem. In particular, most of the popular public key ciphers are based on the difficulty of factoring integers or the discrete logarithm problem, both of which can be solved by Shor's algorithm. In particular, the RSA, Diffie–Hellman, and elliptic curve Diffie–Hellman algorithms could be broken. These are used to protect secure Web pages, encrypted email, and many other types of data. Breaking these would have significant ramifications for electronic privacy and security.

用以加强公开密码匙加密系统安全性的整数分解，如果大型整数是少数素数的乘积(例如两个300位素数的乘积) ，相信在普通电脑上是不可行的。通过比较，量子计算机可以有效地解决这个问题使用肖尔的算法找到它的因素。这种能力将使量子计算机能够破解目前使用的许多密码系统，因为解决这个问题需要多项式时间(整数位数)。特别是，大多数流行的公钥密码都是基于整数因式分解的困难性或者离散对数问题，这两个问题都可以通过 Shor 的算法解决。特别是 RSA、 Diffie-Hellman 和椭圆曲线 Diffie-Hellman 算法可能被破解。它们用于保护安全网页、加密电子邮件和许多其他类型的数据。打破这些限制将对电子隐私和安全产生重大影响。

However, other cryptographic algorithms do not appear to be broken by those algorithms. Some public-key algorithms are based on problems other than the integer factorization and discrete logarithm problems to which Shor's algorithm applies, like the McEliece cryptosystem based on a problem in coding theory. Lattice-based cryptosystems are also not known to be broken by quantum computers, and finding a polynomial time algorithm for solving the dihedral hidden subgroup problem, which would break many lattice based cryptosystems, is a well-studied open problem. It has been proven that applying Grover's algorithm to break a symmetric (secret key) algorithm by brute force requires time equal to roughly 2^n/2 invocations of the underlying cryptographic algorithm, compared with roughly 2ⁿ in the classical case, meaning that symmetric key lengths are effectively halved: AES-256 would have the same security against an attack using Grover's algorithm that AES-128 has against classical brute-force search (see Key size).

However, other cryptographic algorithms do not appear to be broken by those algorithms. Some public-key algorithms are based on problems other than the integer factorization and discrete logarithm problems to which Shor's algorithm applies, like the McEliece cryptosystem based on a problem in coding theory. Lattice-based cryptosystems are also not known to be broken by quantum computers, and finding a polynomial time algorithm for solving the dihedral hidden subgroup problem, which would break many lattice based cryptosystems, is a well-studied open problem. It has been proven that applying Grover's algorithm to break a symmetric (secret key) algorithm by brute force requires time equal to roughly 2^n/2 invocations of the underlying cryptographic algorithm, compared with roughly 2ⁿ in the classical case, meaning that symmetric key lengths are effectively halved: AES-256 would have the same security against an attack using Grover's algorithm that AES-128 has against classical brute-force search (see Key size).

但是，其他加密算法似乎不会被这些算法破解。一些公开密钥算法是基于问题以外的其他问题，而不是 Shor 的算法所适用的整数分解和离散对数问题，比如基于编码理论中的一个问题的 McEliece 密码系统。基于格的密码体制也不为量子计算机所破解，找到一个解决二面体隐子群问题的多项式时间算法，将破坏许多基于格的密码体制，是一个被广泛研究的开放问题。已经证明，应用 Grover 的算法通过暴力破解对称密钥(secret Key)算法需要的时间大约等于底层密码算法的2 sup n / 2 / sup 调用，相比之下，在经典情况下大约需要2 sup n / sup，这意味着对称密钥长度被有效地减半: 使用 Grover 的算法，AES-256对攻击的安全性与 AES-128对经典暴力搜索法的攻击相同(见 Key size)。

Quantum cryptography could potentially fulfill some of the functions of public key cryptography. Quantum-based cryptographic systems could, therefore, be more secure than traditional systems against quantum hacking.

Quantum cryptography could potentially fulfill some of the functions of public key cryptography. Quantum-based cryptographic systems could, therefore, be more secure than traditional systems against quantum hacking.

量子密码学可以实现公开密钥加密的一些功能。因此，基于量子的加密系统可能比传统系统更安全，可以抵御量子黑客攻击。

Quantum search

量子搜索

Besides factorization and discrete logarithms, quantum algorithms offering a more than polynomial speedup over the best known classical algorithm have been found for several problems, including the simulation of quantum physical processes from chemistry and solid state physics, the approximation of Jones polynomials, and solving Pell's equation. No mathematical proof has been found that shows that an equally fast classical algorithm cannot be discovered, although this is considered unlikely. However, quantum computers offer polynomial speedup for some problems. The most well-known example of this is quantum database search, which can be solved by Grover's algorithm using quadratically fewer queries to the database than that are required by classical algorithms. In this case, the advantage is not only provable but also optimal, it has been shown that Grover's algorithm gives the maximal possible probability of finding the desired element for any number of oracle lookups. Several other examples of provable quantum speedups for query problems have subsequently been discovered, such as for finding collisions in two-to-one functions and evaluating NAND trees.

}}</ref> However, quantum computers offer polynomial speedup for some problems. The most well-known example of this is quantum database search, which can be solved by Grover's algorithm using quadratically fewer queries to the database than that are required by classical algorithms. In this case, the advantage is not only provable but also optimal, it has been shown that Grover's algorithm gives the maximal possible probability of finding the desired element for any number of oracle lookups. Several other examples of provable quantum speedups for query problems have subsequently been discovered, such as for finding collisions in two-to-one functions and evaluating NAND trees.

然而，量子计算机为一些问题提供了多项式加速。这方面最著名的例子是量子数据库搜索，它可以通过 Grover 的算法解决，使用比经典算法所需要的数据库查询二次减少。在这种情况下，该算法的优点不仅是可证明的，而且是最优的。随后又发现了其他几个可证明的量子加速比的例子，例如在二对一函数中发现碰撞和计算 NAND 树。

Problems that can be addressed with Grover's algorithm have the following properties:

Problems that can be addressed with Grover's algorithm have the following properties:

可以用 Grover 的算法解决的问题有以下属性:

1. There is no searchable structure in the collection of possible answers,

There is no searchable structure in the collection of possible answers,

在可能的答案的集合中没有可搜索的结构,

1. The number of possible answers to check is the same as the number of inputs to the algorithm, and

The number of possible answers to check is the same as the number of inputs to the algorithm, and

要检查的可能答案的数量与算法的输入数量相同，以及

1. There exists a boolean function which evaluates each input and determines whether it is the correct answer

There exists a boolean function which evaluates each input and determines whether it is the correct answer

存在一个布尔函数，它评估每个输入，并确定它是否是正确的答案

For problems with all these properties, the running time of Grover's algorithm on a quantum computer will scale as the square root of the number of inputs (or elements in the database), as opposed to the linear scaling of classical algorithms. A general class of problems to which Grover's algorithm can be applied is Boolean satisfiability problem. In this instance, the database through which the algorithm is iterating is that of all possible answers. An example (and possible) application of this is a password cracker that attempts to guess the password or secret key for an encrypted file or system. Symmetric ciphers such as Triple DES and AES are particularly vulnerable to this kind of attack. This application of quantum computing is a major interest of government agencies.

For problems with all these properties, the running time of Grover's algorithm on a quantum computer will scale as the square root of the number of inputs (or elements in the database), as opposed to the linear scaling of classical algorithms. A general class of problems to which Grover's algorithm can be applied is Boolean satisfiability problem. In this instance, the database through which the algorithm is iterating is that of all possible answers. An example (and possible) application of this is a password cracker that attempts to guess the password or secret key for an encrypted file or system. Symmetric ciphers such as Triple DES and AES are particularly vulnerable to this kind of attack. This application of quantum computing is a major interest of government agencies.

对于具有所有这些特性的问题，Grover 算法在量子计算机上的运行时间将作为输入数量(或数据库中的元素)的平方根，而不是经典算法的线性缩放。的算法可以应用到的一类通用问题是布尔可满足性问题问题。在这个例子中，算法迭代的数据库是所有可能的答案的数据库。这方面的一个示例(和可能的)应用程序是密码破解器，它试图猜测加密文件或系统的密码或密钥。对称密码如三重 DES 和 AES 特别容易受到这种攻击。量子计算的这种应用是政府机构的主要兴趣所在。

Quantum simulation

Main article: Quantum simulator

Since chemistry and nanotechnology rely on understanding quantum systems, and such systems are impossible to simulate in an efficient manner classically, many believe quantum simulation will be one of the most important applications of quantum computing. Quantum simulation could also be used to simulate the behavior of atoms and particles at unusual conditions such as the reactions inside a collider.

Since chemistry and nanotechnology rely on understanding quantum systems, and such systems are impossible to simulate in an efficient manner classically, many believe quantum simulation will be one of the most important applications of quantum computing. Quantum simulation could also be used to simulate the behavior of atoms and particles at unusual conditions such as the reactions inside a collider.

由于化学和纳米技术依赖于对量子系统的理解，而这样的系统是不可能以有效的经典方式进行模拟的，许多人相信量子模拟将是量子计算最重要的应用之一。量子模拟也可以用来模拟原子和粒子在非正常条件下的行为，比如对撞机内部的反应。

Quantum annealing and adiabatic optimization

量子退火和绝热优化

Quantum annealing or Adiabatic quantum computation relies on the adiabatic theorem to undertake calculations. A system is placed in the ground state for a simple Hamiltonian, which is slowly evolved to a more complicated Hamiltonian whose ground state represents the solution to the problem in question. The adiabatic theorem states that if the evolution is slow enough the system will stay in its ground state at all times through the process.

Quantum annealing or Adiabatic quantum computation relies on the adiabatic theorem to undertake calculations. A system is placed in the ground state for a simple Hamiltonian, which is slowly evolved to a more complicated Hamiltonian whose ground state represents the solution to the problem in question. The adiabatic theorem states that if the evolution is slow enough the system will stay in its ground state at all times through the process.

量子退火或绝热量子计算依赖于绝热定理进行计算。对于一个简单的哈密顿量，一个系统被放置在基态，这个哈密顿量慢慢演化成一个更复杂的哈密顿量，它的基态代表问题的解。绝热定理指出，如果演化足够慢，系统在整个演化过程中将始终处于基态。

Solving linear equations

求解线性方程组

The Quantum algorithm for linear systems of equations, or "HHL Algorithm", named after its discoverers Harrow, Hassidim, and Lloyd, is expected to provide speedup over classical counterparts.

The Quantum algorithm for linear systems of equations, or "HHL Algorithm", named after its discoverers Harrow, Hassidim, and Lloyd, is expected to provide speedup over classical counterparts.

以其发现者 Harrow，Hassidim 和 Lloyd 命名的线性方程组的量子算法，或称“ HHL 算法” ，预计将提供比传统算法更快的速度。

Quantum supremacy

量子优势

Main article: Quantum supremacy

John Preskill has introduced the term quantum supremacy to refer to the hypothetical speedup advantage that a quantum computer would have over a classical computer in a certain field. Google announced in 2017 that it expected to achieve quantum supremacy by the end of the year though that did not happen. IBM said in 2018 that the best classical computers will be beaten on some practical task within about five years and views the quantum supremacy test only as a potential future benchmark. Although skeptics like Gil Kalai doubt that quantum supremacy will ever be achieved, in October 2019, a Sycamore processor created in conjunction with Google AI Quantum was reported to have achieved quantum supremacy, with calculations more than 3,000,000 times as fast as those of Summit, generally considered the world's fastest computer. Bill Unruh doubted the practicality of quantum computers in a paper published back in 1994. Paul Davies argued that a 400-qubit computer would even come into conflict with the cosmological information bound implied by the holographic principle.

John Preskill has introduced the term quantum supremacy to refer to the hypothetical speedup advantage that a quantum computer would have over a classical computer in a certain field. Google announced in 2017 that it expected to achieve quantum supremacy by the end of the year though that did not happen. IBM said in 2018 that the best classical computers will be beaten on some practical task within about five years and views the quantum supremacy test only as a potential future benchmark. Although skeptics like Gil Kalai doubt that quantum supremacy will ever be achieved, in October 2019, a Sycamore processor created in conjunction with Google AI Quantum was reported to have achieved quantum supremacy, with calculations more than 3,000,000 times as fast as those of Summit, generally considered the world's fastest computer. Bill Unruh doubted the practicality of quantum computers in a paper published back in 1994. Paul Davies argued that a 400-qubit computer would even come into conflict with the cosmological information bound implied by the holographic principle.

约翰 · 普雷斯基尔提出了量子优势这一术语，指的是量子计算机在某一领域相对于经典计算机的假设加速优势。谷歌在2017年宣布，它希望在今年年底前实现量子优势，尽管这一目标没有实现。Ibm 在2018年表示，最好的经典计算机将在大约5年内在某些实际任务上被击败，并将量子优势测试视为未来的潜在基准。尽管像吉尔 · 卡莱这样的怀疑者对量子优势的实现持怀疑态度，但在2019年10月，据报道，与谷歌人工智能量子公司合作开发的 Sycamore 处理器已经取得了量子优势，其计算速度是顶峰计算机的300万倍以上，顶峰计算机被公认为世界上最快的计算机。比尔 · 安鲁在1994年发表的一篇论文中对量子计算机的实用性表示怀疑。认为，一台400量子位的计算机甚至可能与美国全息原理协会暗示的宇宙学信息发生冲突。

Obstacles

障碍

There are a number of technical challenges in building a large-scale quantum computer. Physicist David DiVincenzo has listed the following requirements for a practical quantum computer:

There are a number of technical challenges in building a large-scale quantum computer. Physicist David DiVincenzo has listed the following requirements for a practical quantum computer:

建造大型量子计算机存在许多技术挑战。物理学家 David DiVincenzo 列出了实用量子计算机的下列要求:

• Scalable physically to increase the number of qubits

• Qubits that can be initialized to arbitrary values

• Quantum gates that are faster than decoherence time

• Universal gate set

• Qubits that can be read easily

Sourcing parts for quantum computers is also very difficult. Many quantum computers, like those constructed by Google and IBM, need Helium-3, a nuclear research byproduct, and special superconducting cables that are only made by a single company in Japan.

Sourcing parts for quantum computers is also very difficult. Many quantum computers, like those constructed by Google and IBM, need Helium-3, a nuclear research byproduct, and special superconducting cables that are only made by a single company in Japan.

寻找量子计算机的零部件也非常困难。许多量子计算机，比如谷歌(Google)和 IBM 制造的计算机，需要核研究的副产品氦 -3(氦 -3) ，以及只有日本一家公司制造的特殊超导电缆。

Quantum decoherence

Main article: Quantum decoherence

One of the greatest challenges involved with constructing quantum computers is controlling or removing quantum decoherence. This usually means isolating the system from its environment as interactions with the external world cause the system to decohere. However, other sources of decoherence also exist. Examples include the quantum gates, and the lattice vibrations and background thermonuclear spin of the physical system used to implement the qubits. Decoherence is irreversible, as it is effectively non-unitary, and is usually something that should be highly controlled, if not avoided. Decoherence times for candidate systems in particular, the transverse relaxation time T₂ (for NMR and MRI technology, also called the dephasing time), typically range between nanoseconds and seconds at low temperature. Currently, some quantum computers require their qubits to be cooled to 20 millikelvins in order to prevent significant decoherence.

One of the greatest challenges involved with constructing quantum computers is controlling or removing quantum decoherence. This usually means isolating the system from its environment as interactions with the external world cause the system to decohere. However, other sources of decoherence also exist. Examples include the quantum gates, and the lattice vibrations and background thermonuclear spin of the physical system used to implement the qubits. Decoherence is irreversible, as it is effectively non-unitary, and is usually something that should be highly controlled, if not avoided. Decoherence times for candidate systems in particular, the transverse relaxation time T₂ (for NMR and MRI technology, also called the dephasing time), typically range between nanoseconds and seconds at low temperature. Currently, some quantum computers require their qubits to be cooled to 20 millikelvins in order to prevent significant decoherence.

构建量子计算机的最大挑战之一是控制或移除量子退相干。这通常意味着将系统与其环境隔离开来，因为与外部世界的相互作用会导致系统解码。然而，退相干的其他来源也存在。例子包括量子门，以及实现量子位的物理系统的晶格振动和背景热核自旋。退相干是不可逆的，因为它实际上是非幺正的，而且通常应该受到高度控制，如果不能避免的话。特别是候选系统的退相干时间，横向弛豫时间 t 小于2 / 子(对于 NMR 和 MRI 技术，也称为退相时间) ，通常在低温下的纳秒到秒之间。目前，一些量子计算机需要将它们的量子比特冷却到20毫升，以防止明显的退相干。

As a result, time-consuming tasks may render some quantum algorithms inoperable, as maintaining the state of qubits for a long enough duration will eventually corrupt the superpositions.

As a result, time-consuming tasks may render some quantum algorithms inoperable, as maintaining the state of qubits for a long enough duration will eventually corrupt the superpositions.

因此，耗时的任务可能会使一些量子算法无法运行，因为维持量子位的状态足够长的时间最终会破坏这些叠加。

These issues are more difficult for optical approaches as the timescales are orders of magnitude shorter and an often-cited approach to overcoming them is optical pulse shaping. Error rates are typically proportional to the ratio of operating time to decoherence time, hence any operation must be completed much more quickly than the decoherence time.

These issues are more difficult for optical approaches as the timescales are orders of magnitude shorter and an often-cited approach to overcoming them is optical pulse shaping. Error rates are typically proportional to the ratio of operating time to decoherence time, hence any operation must be completed much more quickly than the decoherence time.

这些问题对于光学方法来说更加困难，因为光学方法的时间数量级更短，而克服这些问题的常用方法是光脉冲整形。错误率通常与操作时间与去相干时间的比例成正比，因此任何操作必须比去相干时间更快地完成。

As described in the Quantum threshold theorem, if the error rate is small enough, it is thought to be possible to use quantum error correction to suppress errors and decoherence. This allows the total calculation time to be longer than the decoherence time if the error correction scheme can correct errors faster than decoherence introduces them. An often cited figure for the required error rate in each gate for fault-tolerant computation is 10⁻³, assuming the noise is depolarizing.

As described in the Quantum threshold theorem, if the error rate is small enough, it is thought to be possible to use quantum error correction to suppress errors and decoherence. This allows the total calculation time to be longer than the decoherence time if the error correction scheme can correct errors faster than decoherence introduces them. An often cited figure for the required error rate in each gate for fault-tolerant computation is 10⁻³, assuming the noise is depolarizing.

正如量子阈值定理所描述的那样，如果误差率足够小，人们认为可以利用量子误差修正来抑制误差和退相干。这允许总计算时间比消相干时间更长，如果纠错方案可以更快地纠正误差比消相干引入误差。在假设噪声是去极化的情况下，容错计算中每个门所需的错误率经常被引用的数字是10 sup-3 / sup。

Meeting this scalability condition is possible for a wide range of systems. However, the use of error correction brings with it the cost of a greatly increased number of required qubits. The number required to factor integers using Shor's algorithm is still polynomial, and thought to be between L and L², where L is the number of qubits in the number to be factored; error correction algorithms would inflate this figure by an additional factor of L. For a 1000-bit number, this implies a need for about 10⁴ bits without error correction. With error correction, the figure would rise to about 10⁷ bits. Computation time is about L² or about 10⁷ steps and at 1 MHz, about 10 seconds.

Meeting this scalability condition is possible for a wide range of systems. However, the use of error correction brings with it the cost of a greatly increased number of required qubits. The number required to factor integers using Shor's algorithm is still polynomial, and thought to be between L and L², where L is the number of qubits in the number to be factored; error correction algorithms would inflate this figure by an additional factor of L. For a 1000-bit number, this implies a need for about 10⁴ bits without error correction. With error correction, the figure would rise to about 10⁷ bits. Computation time is about L² or about 10⁷ steps and at 1 MHz, about 10 seconds.

对于许多系统来说，满足这种可伸缩性条件是可能的。然而，错误校正的使用带来了大大增加所需量子位数的成本。使用 Shor 算法对整数进行因子分解所需要的数字仍然是多项式的，并且被认为介于 l 和 l sup 2 / sup 之间，其中 l 是要分解的数字中的量子位数; 错误校正算法将使这个数字膨胀一个额外的因子 l。对于一个1000位的数字，这意味着需要大约10个 sup 4 / sup 位而不需要纠错。通过纠错，这个数字将上升到大约10 sup 7 / sup 位。计算时间是大约 l sup 2 / sup 或大约10 sup 7 / sup steps，在1mhz，大约10秒。

A very different approach to the stability-decoherence problem is to create a topological quantum computer with anyons, quasi-particles used as threads and relying on braid theory to form stable logic gates.

| year = 2003}}</ref>

| year 2003} / ref

Physicist Mikhail Dyakonov has expressed skepticism of quantum computing as follows:

Physicist Mikhail Dyakonov has expressed skepticism of quantum computing as follows:

物理学家米哈伊尔 · 迪亚科诺夫对量子计算表示怀疑如下:

"So the number of continuous parameters describing the state of such a useful quantum computer at any given moment must be... about 10³⁰⁰... Could we ever learn to control the more than 10³⁰⁰ continuously variable parameters defining the quantum state of such a system? My answer is simple. No, never."

"So the number of continuous parameters describing the state of such a useful quantum computer at any given moment must be... about 10³⁰⁰... Could we ever learn to control the more than 10³⁰⁰ continuously variable parameters defining the quantum state of such a system? My answer is simple. No, never."

“因此，描述这样一台有用的量子计算机在任何给定时刻的状态的连续参数的数量必须是... ... 大约10 × 300 × 10300 × 10300 × 10300 × 10300 × 10300 × 10300 × 10300的连续可变参数定义了这样一个系统的？我的答案很简单。不，永远不会。”

Developments

事态发展

Quantum computing models

量子计算模型

There are a number of quantum computing models, distinguished by the basic elements in which the computation is decomposed. The four main models of practical importance are:

There are a number of quantum computing models, distinguished by the basic elements in which the computation is decomposed. The four main models of practical importance are:

有许多量子计算模型，以计算被分解的基本元素来区分。具有实际重要性的四个主要模式是:

• Quantum gate array (computation decomposed into a sequence of few-qubit quantum gates)

• One-way quantum computer (computation decomposed into a sequence of one-qubit measurements applied to a highly entangled initial state or cluster state)

• Adiabatic quantum computer, based on quantum annealing (computation decomposed into a slow continuous transformation of an initial Hamiltonian into a final Hamiltonian, whose ground states contain the solution)

• Topological quantum computer (computation decomposed into the braiding of anyons in a 2D lattice)

|issue = 3 }}</ref> (computation decomposed into the braiding of anyons in a 2D lattice)

/ ref (计算分解为二维点阵中任意子的编织)

The quantum Turing machine is theoretically important but the physical implementation of this model is not feasible. All four models of computation have been shown to be equivalent; each can simulate the other with no more than polynomial overhead.

The quantum Turing machine is theoretically important but the physical implementation of this model is not feasible. All four models of computation have been shown to be equivalent; each can simulate the other with no more than polynomial overhead.

量子图灵机在理论上是重要的，但是这个模型的实际实施是不可行的。所有四种计算模型都被证明是等价的; 每种模型只需多项式开销就可以模拟另一种模型。

Physical realizations

物理实现

For physically implementing a quantum computer, many different candidates are being pursued, among them (distinguished by the physical system used to realize the qubits):

For physically implementing a quantum computer, many different candidates are being pursued, among them (distinguished by the physical system used to realize the qubits):

为了实现量子计算机的物理实现，许多不同的候选者被追求，其中包括(区别于用于实现量子位的物理系统) :

• Superconducting quantum computing (qubit implemented by the state of small superconducting circuits (Josephson junctions)

}}</ref> (qubit implemented by the state of small superconducting circuits (Josephson junctions)

} / ref (由小型超导电路(约瑟夫森结)实现的量子比特)

• Trapped ion quantum computer (qubit implemented by the internal state of trapped ions)

• Optical lattices (qubit implemented by internal states of neutral atoms trapped in an optical lattice)

• Quantum dot computer, spin-based (e.g. the Loss-DiVincenzo quantum computer) (qubit given by the spin states of trapped electrons)

• Quantum dot computer, spatial-based (qubit given by electron position in double quantum dot)

• Coupled Quantum Wire (qubit implemented by a pair of Quantum Wires coupled by a Quantum Point Contact)

• Nuclear magnetic resonance quantum computer (NMRQC) implemented with the nuclear magnetic resonance of molecules in solution, where qubits are provided by nuclear spins within the dissolved molecule and probed with radio waves

• Solid-state NMR Kane quantum computers (qubit realized by the nuclear spin state of phosphorus donors in silicon)

• Electrons-on-helium quantum computers (qubit is the electron spin)

• Cavity quantum electrodynamics (CQED) (qubit provided by the internal state of trapped atoms coupled to high-finesse cavities)

• Molecular magnet (qubit given by spin states)

• Fullerene-based ESR quantum computer (qubit based on the electronic spin of atoms or molecules encased in fullerenes)

• Linear optical quantum computer (qubits realized by processing states of different modes of light through linear elements e.g. mirrors, beam splitters and phase shifters)

• Diamond-based quantum computer (qubit realized by the electronic or nuclear spin of nitrogen-vacancy centers in diamond)

|first9 = F. }}</ref> (qubit realized by the electronic or nuclear spin of nitrogen-vacancy centers in diamond)

| first9 f } / ref (由金刚石中氮空位中心的电子自旋或核自旋实现的量子比特)

• Bose-Einstein condensate-based quantum computer

• Transistor-based quantum computer – string quantum computers with entrainment of positive holes using an electrostatic trap

• Rare-earth-metal-ion-doped inorganic crystal based quantum computers (qubit realized by the internal electronic state of dopants in optical fibers)

|arxiv = quant-ph/0404083 |bibcode = 2004PhRvL..93m0503L }}</ref> (qubit realized by the internal electronic state of dopants in optical fibers)

| arxiv quant-ph / 0404083 | bibcode 2004PhRvL. . 93 m0503L } / ref (qubit 由光纤中掺杂剂的内部电子状态实现)

• Metallic-like carbon nanospheres based quantum computers

A large number of candidates demonstrates that quantum computing, despite rapid progress, is still in its infancy.

A large number of candidates demonstrates that quantum computing, despite rapid progress, is still in its infancy.

大量的候选者表明，量子计算，尽管进展迅速，仍然处于初级阶段。

Relation to computability and complexity theory

与可计算性和复杂性理论的关系

Computability theory

可计算性理论

See also: Computability theory

Any computational problem solvable by a classical computer is also solvable by a quantum computer. Intuitively, this is because it is believed that all physical phenomena, including the operation of classical computers, can be described using quantum mechanics, which underlies the operation of quantum computers.

Any computational problem solvable by a classical computer is also solvable by a quantum computer. Intuitively, this is because it is believed that all physical phenomena, including the operation of classical computers, can be described using quantum mechanics, which underlies the operation of quantum computers.

任何经典计算机可解的计算问题也可以用量子计算机来解。直观地说，这是因为人们相信所有的物理现象，包括经典计算机的运算，都可以用量子计算机运算的基础---- 量子力学来描述。

Conversely, any problem solvable by a quantum computer is also solvable by a classical computer, or more formally any quantum computer can be simulated by a Turing machine. In other words, quantum computers provide no additional power over classical computers in terms of computability. This means that quantum computers cannot solve undecidable problems like the halting problem and the existence of quantum computers does not disprove the Church–Turing thesis.

Conversely, any problem solvable by a quantum computer is also solvable by a classical computer, or more formally any quantum computer can be simulated by a Turing machine. In other words, quantum computers provide no additional power over classical computers in terms of computability. This means that quantum computers cannot solve undecidable problems like the halting problem and the existence of quantum computers does not disprove the Church–Turing thesis.

相反，任何量子计算机可以解决的问题也可以用经典计算机来解决，或者更正式地说，任何量子计算机都可以用图灵机来模拟。换句话说，就可计算性而言，量子计算机并不比传统计算机提供额外的能力。这意味着量子计算机不能解决不可判定的问题，比如停机问题和量子计算机的存在并不能否定丘奇-图灵理论。

As of yet, quantum computers do not satisfy the strong Church thesis. While hypothetical machines have been realized, these machines cannot be constructed in reality. The strong version of Church's thesis requires these machines to be physical, therefore these hypothetical machines cannot represent a quantum computer that satisfies the strong Church thesis.

As of yet, quantum computers do not satisfy the strong Church thesis. While hypothetical machines have been realized, these machines cannot be constructed in reality. The strong version of Church's thesis requires these machines to be physical, therefore these hypothetical machines cannot represent a quantum computer that satisfies the strong Church thesis.

到目前为止，量子计算机还不能满足教会强有力的论点。虽然假设的机器已经实现，但这些机器不能在现实中构造。丘奇论点的强有力版本要求这些机器是物理的，因此这些假设的机器不能代表一个满足强有力的丘奇论点的量子计算机。

Quantum complexity theory

量子复杂性理论

Main article: Quantum complexity theory

! ——量子计算机的能力和极限——

While quantum computers cannot solve any problems that classical computers cannot already solve, it is suspected that they can solve many problems faster than classical computers. For instance, it is known that quantum computers can efficiently factor integers, while this is not believed to be the case for classical computers. However, the capacity of quantum computers to accelerate classical algorithms has rigid upper bounds, and the overwhelming majority of classical calculations cannot be accelerated by the use of quantum computers.

While quantum computers cannot solve any problems that classical computers cannot already solve, it is suspected that they can solve many problems faster than classical computers. For instance, it is known that quantum computers can efficiently factor integers, while this is not believed to be the case for classical computers. However, the capacity of quantum computers to accelerate classical algorithms has rigid upper bounds, and the overwhelming majority of classical calculations cannot be accelerated by the use of quantum computers.

虽然量子计算机不能解决任何传统计算机已经不能解决的问题，人们怀疑它们能比传统计算机更快地解决许多问题。例如，众所周知量子计算机可以有效地对整数进行因子分解，而经典计算机则不然。然而，量子计算机加速经典算法的能力具有严格的上限，绝大多数经典计算不能被量子计算机加速。

! -- bqp 的基本定义 --

The class of problems that can be efficiently solved by a quantum computer with bounded error is called BQP, for "bounded error, quantum, polynomial time". More formally, BQP is the class of problems that can be solved by a polynomial-time quantum Turing machine with error probability of at most 1/3. As a class of probabilistic problems, BQP is the quantum counterpart to BPP ("bounded error, probabilistic, polynomial time"), the class of problems that can be efficiently solved by probabilistic Turing machines with bounded error. It is known that BPP[math]\displaystyle{ \subseteq }[/math]BQP and widely suspected, but not proven, that BQP[math]\displaystyle{ \nsubseteq }[/math]BPP, which intuitively would mean that quantum computers are more powerful than classical computers in terms of time complexity.

The class of problems that can be efficiently solved by a quantum computer with bounded error is called BQP, for "bounded error, quantum, polynomial time". More formally, BQP is the class of problems that can be solved by a polynomial-time quantum Turing machine with error probability of at most 1/3. As a class of probabilistic problems, BQP is the quantum counterpart to BPP ("bounded error, probabilistic, polynomial time"), the class of problems that can be efficiently solved by probabilistic Turing machines with bounded error. It is known that BPP[math]\displaystyle{ \subseteq }[/math]BQP and widely suspected, but not proven, that BQP[math]\displaystyle{ \nsubseteq }[/math]BPP, which intuitively would mean that quantum computers are more powerful than classical computers in terms of time complexity.

有界误差量子计算机能够有效地求解的一类问题称为 BQP 问题，具有“有界误差、量子、多项式时间”的特点。更正式地说，BQP 是一类问题，可以用多项式时间量子图灵机来解决，错误概率最多为1 / 3。作为一类概率问题，BQP 是 BPP (“有界误差，概率，多项式时间”)的量子对应物，BPP 是一类具有有界误差的概率图灵机能够有效求解的问题。众所周知，量子计算机在时间复杂度方面比传统计算机更为强大，人们普遍怀疑量子计算机在时间复杂度方面比传统计算机更强大，但并未得到证实。

! -- bqp 与基本复杂性类的关系 --

The suspected relationship of BQP to several classical complexity classes.

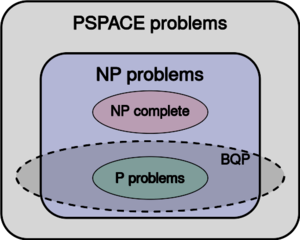
The suspected relationship of BQP to several classical complexity classes.

Bqp 与几个经典复杂类的可疑关系。

The exact relationship of BQP to P, NP, and PSPACE is not known. However, it is known that P[math]\displaystyle{ \subseteq }[/math]BQP[math]\displaystyle{ \subseteq }[/math]PSPACE; that is, the class of problems that can be efficiently solved by quantum computers includes all problems that can be efficiently solved by deterministic classical computers but does not include any problems that cannot be solved by classical computers with polynomial space resources. It is further suspected that BQP is a strict superset of P, meaning there are problems that are efficiently solvable by quantum computers that are not efficiently solvable by deterministic classical computers. For instance, integer factorization and the discrete logarithm problem are known to be in BQP and are suspected to be outside of P. On the relationship of BQP to NP, little is known beyond the fact that some NP problems are in BQP (integer factorization and the discrete logarithm problem are both in NP, for example). It is suspected that NP[math]\displaystyle{ \nsubseteq }[/math]BQP; that is, it is believed that there are efficiently checkable problems that are not efficiently solvable by a quantum computer. As a direct consequence of this belief, it is also suspected that BQP is disjoint from the class of NP-complete problems (if an NP-complete problem were in BQP, then it follows from NP-hardness that all problems in NP are in BQP).

The exact relationship of BQP to P, NP, and PSPACE is not known. However, it is known that P[math]\displaystyle{ \subseteq }[/math]BQP[math]\displaystyle{ \subseteq }[/math]PSPACE; that is, the class of problems that can be efficiently solved by quantum computers includes all problems that can be efficiently solved by deterministic classical computers but does not include any problems that cannot be solved by classical computers with polynomial space resources. It is further suspected that BQP is a strict superset of P, meaning there are problems that are efficiently solvable by quantum computers that are not efficiently solvable by deterministic classical computers. For instance, integer factorization and the discrete logarithm problem are known to be in BQP and are suspected to be outside of P. On the relationship of BQP to NP, little is known beyond the fact that some NP problems are in BQP (integer factorization and the discrete logarithm problem are both in NP, for example). It is suspected that NP[math]\displaystyle{ \nsubseteq }[/math]BQP; that is, it is believed that there are efficiently checkable problems that are not efficiently solvable by a quantum computer. As a direct consequence of this belief, it is also suspected that BQP is disjoint from the class of NP-complete problems (if an NP-complete problem were in BQP, then it follows from NP-hardness that all problems in NP are in BQP).

Bqp 与 p、 NP 和 PSPACE 的确切关系尚不清楚。然而，众所周知 p math subseteq / math BQP math subseteq / math PSPACE; 也就是说，量子计算机可以有效地解决的问题包括所有可以由确定性经典计算机有效地解决的问题，但不包括任何不能由拥有 PSPACE 资源的经典计算机解决的问题。进一步怀疑 BQP 是 p 的严格超集，这意味着有些问题可以通过量子计算机有效地解决，而这些问题不能通过确定性经典计算机有效地解决。例如，整数分解问题和离散对数问题都已知在 BQP 中，并且被怀疑在 p 之外。关于 BQP 与 NP 的关系，除了一些 NP 问题在 BQP 中之外，我们知之甚少(例如，整数分解和离散对数问题都在 NP 中)。人们怀疑 NP 数学 nsubseteq / math BQP，也就是说，人们相信存在有效的检验问题，而量子计算机不能有效地解决这些问题。作为这一信念的直接结果，我们还怀疑 BQP 与 NP 完全问题不相交(如果一个 NP 完全问题存在于 BQP 中，那么由 NP 完全问题存在于 BQP 中)。

! ——与基本复杂性类的关系概述——

The relationship of BQP to the basic classical complexity classes can be summarized as:

The relationship of BQP to the basic classical complexity classes can be summarized as:

Bqp 与基本经典复杂性类的关系可以概括为:

[math]\displaystyle{ \mathsf{P \subseteq BPP \subseteq BQP \subseteq PP \subseteq PSPACE} }[/math]

[math]\displaystyle{ \mathsf{P \subseteq BPP \subseteq BQP \subseteq PP \subseteq PSPACE} }[/math]

数学{ p subseteq BPP subseteq BQP subseteq PP subseteq PSPACE } / math

It is also known that BQP is contained in the complexity class #P (or more precisely in the associated class of decision problems P^#P), which is a subclass of PSPACE.

It is also known that BQP is contained in the complexity class #P (or more precisely in the associated class of decision problems P^#P), which is a subclass of PSPACE.

我们还知道，BQP 包含在复杂性类 # p 中(或者更确切地说是决策问题 p sup # p / sup 的关联类中) ，这是 PSPACE 的一个子类。

! ——对更先进类型量子计算机的推测——

It has been speculated that further advances in physics could lead to even faster computers. For instance, it has been shown that a non-local hidden variable quantum computer based on Bohmian Mechanics could implement a search of an N-item database in at most [math]\displaystyle{ O(\sqrt[3]{N}) }[/math] steps, a slight speedup over Grover's algorithm, which runs in [math]\displaystyle{ O(\sqrt{N}) }[/math] steps. Note, however, that neither search method would allow quantum computers to solve NP-complete problems in polynomial time. Theories of quantum gravity, such as M-theory and loop quantum gravity, may allow even faster computers to be built. However, defining computation in these theories is an open problem due to the problem of time; that is, within these physical theories there is currently no obvious way to describe what it means for an observer to submit input to a computer at one point in time and then receive output at a later point in time.

It has been speculated that further advances in physics could lead to even faster computers. For instance, it has been shown that a non-local hidden variable quantum computer based on Bohmian Mechanics could implement a search of an N-item database in at most [math]\displaystyle{ O(\sqrt[3]{N}) }[/math] steps, a slight speedup over Grover's algorithm, which runs in [math]\displaystyle{ O(\sqrt{N}) }[/math] steps. Note, however, that neither search method would allow quantum computers to solve NP-complete problems in polynomial time. Theories of quantum gravity, such as M-theory and loop quantum gravity, may allow even faster computers to be built. However, defining computation in these theories is an open problem due to the problem of time; that is, within these physical theories there is currently no obvious way to describe what it means for an observer to submit input to a computer at one point in time and then receive output at a later point in time.

据推测，物理学的进一步发展可能会导致计算机速度更快。例如，已经证明，基于 Bohmian Mechanics 的非局部隐变量量子计算机最多只能执行数学 o ( sqrt [3]{ n }) / 数学步骤中的 n 项数据库搜索，这比 Grover 运行在数学 o ( sqrt { n } / 数学步骤中的算法稍微快了一点。然而，请注意，这两种搜索方法都不允许量子计算机在多项式时间内解决 np 完全问题。量子引力理论，如 m 理论和回圈量子重力理论，可能允许建造更快的计算机。然而，由于时间问题，在这些理论中定义计算是一个开放的问题; 也就是说，在这些物理理论中，目前没有明显的方法来描述观察者在一个时间点向计算机提交输入，然后在稍后的时间点接收输出意味着什么。

See also

参见

! -- 请按字母顺序添加新链接 --

{ columns-list

The unnamed parameter 2= is no longer supported. Please see the documentation for {{columns-list}}.

colwidth 20em

}}

References

参考资料

Further reading

进一步阅读

Textbooks

教科书

• Nielsen, Michael; Chuang, Isaac (2000). Quantum Computation and Quantum Information. Cambridge: Cambridge University Press. ISBN 978-0-521-63503-5. OCLC 174527496. https://books.google.com/books?id=aai-P4V9GJ8C&printsec=frontcover. 

• Mermin, N. David (2007). Quantum Computer Science: An Introduction. Cambridge University Press. ISBN 978-0-521-87658-2. 

• Akama, Seiki (2014). Elements of Quantum Computing: History, Theories and Engineering Applications. Springer International Publishing. ISBN 978-3-319-08284-4. 

• Benenti, Giuliano (2004). Principles of Quantum Computation and Information Volume 1. New Jersey: World Scientific. ISBN 978-981-238-830-8. OCLC 179950736. 

• Stolze, Joachim; Suter, Dieter (2004). Quantum Computing. Wiley-VCH. ISBN 978-3-527-40438-4. 

• Wichert, Andreas (2014). Principles of Quantum Artificial Intelligence. World Scientific Publishing Co.. ISBN 978-981-4566-74-2. 

• Hiroshi, Imai; Masahito, Hayashi (2006). Quantum Computation and Information. Berlin: Springer. ISBN 978-3-540-33132-2. 

• Jaeger, Gregg (2006). Quantum Information: An Overview. Berlin: Springer. ISBN 978-0-387-35725-6. OCLC 255569451. 

Academic papers

学术论文

• Abbot, Derek; Doering, Charles R.; Caves, Carlton M.; Lidar, Daniel M.; Brandt, Howard E.; Hamilton, Alexander R.; Ferry, David K.; Gea-Banacloche, Julio; Bezrukov, Sergey M.; Kish, Laszlo B. (2003). "Dreams versus Reality: Plenary Debate Session on Quantum Computing". Quantum Information Processing. 2 (6): 449–472. arXiv:quant-ph/0310130. doi:10.1023/B:QINP.0000042203.24782.9a. hdl:2027.42/45526.

• DiVincenzo, David P. (2000). "The Physical Implementation of Quantum Computation". Fortschritte der Physik. 48 (9–11): 771–783. arXiv:quant-ph/0002077. Bibcode:2000ForPh..48..771D. doi:10.1002/1521-3978(200009)48:9/11<771::AID-PROP771>3.0.CO;2-E.

• Berthiaume, Andre (1997). "Quantum Computation".

• DiVincenzo, David P. (1995). "Quantum Computation". Science. 270 (5234): 255–261. Bibcode:1995Sci...270..255D. CiteSeerX 10.1.1.242.2165. doi:10.1126/science.270.5234.255. Table 1 lists switching and dephasing times for various systems.

• Feynman, Richard (1982). "Simulating physics with computers". International Journal of Theoretical Physics. 21 (6–7): 467–488. Bibcode:1982IJTP...21..467F. CiteSeerX 10.1.1.45.9310. doi:10.1007/BF02650179.

• Mitchell, Ian (1998). "Computing Power into the 21st Century: Moore's Law and Beyond".

• Simon, Daniel R. (1994). "On the Power of Quantum Computation". Institute of Electrical and Electronic Engineers Computer Society Press.

External links

外部链接

• Stanford Encyclopedia of Philosophy: "Quantum Computing" by Amit Hagar and Michael E. Cuffaro.

• 模板:Springer

• Quantum computing for the very curious by Andy Matuschak and Michael Nielsen

Lectures

Lectures

讲座

• Quantum computing for the determined – 22 video lectures by Michael Nielsen

• Video Lectures by David Deutsch

• Lectures at the Institut Henri Poincaré (slides and videos)

• Online lecture on An Introduction to Quantum Computing, Edward Gerjuoy (2008)

• Lomonaco, Sam. Four Lectures on Quantum Computing given at Oxford University in July 2006

Category:Models of computation

类别: 计算模型

Category:Quantum cryptography

类别: 量子密码学

Category:Information theory

范畴: 信息论

Category:Computational complexity theory

类别: 计算复杂性理论

Category:Classes of computers

类别: 电脑类别

Category:Theoretical computer science

类别: 理论计算机科学

Category:Open problems

类别: 开放性问题

Category:Computer-related introductions in 1980

类别: 1980年与计算机有关的介绍

Category:Emerging technologies

类别: 新兴技术

This page was moved from wikipedia:en:Quantum computing. Its edit history can be viewed at 量子计算/edithistory