条件互信息

此词条暂由彩云小译翻译，未经人工整理和审校，带来阅读不便，请见谅。模板:Information theory

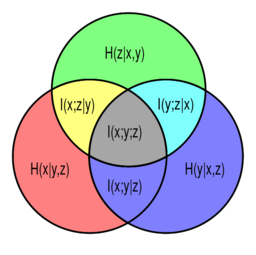
Venn diagram of information theoretic measures for three variables [math]\displaystyle{ x }[/math], [math]\displaystyle{ y }[/math], and [math]\displaystyle{ z }[/math], represented by the lower left, lower right, and upper circles, respectively. The conditional mutual informations [math]\displaystyle{ I(x;z|y) }[/math], [math]\displaystyle{ I(y;z|x) }[/math] and [math]\displaystyle{ I(x;y|z) }[/math] are represented by the yellow, cyan, and magenta regions, respectively.

[[Venn diagram of information theoretic measures for three variables [math]\displaystyle{ x }[/math], [math]\displaystyle{ y }[/math], and [math]\displaystyle{ z }[/math], represented by the lower left, lower right, and upper circles, respectively. The conditional mutual informations [math]\displaystyle{ I(x;z|y) }[/math], [math]\displaystyle{ I(y;z|x) }[/math] and [math]\displaystyle{ I(x;y|z) }[/math] are represented by the yellow, cyan, and magenta regions, respectively.]]

[文恩图表信息理论测量三个变量的数学 x / math，math y / math，和 math z / math，分别由左下角，右下角和上面的圆圈表示。条件互信息 math i (x; z | y) / math i (y; z | x) / math i (x; y | z) / math i (x; y | z) / math 分别由黄色、青色和品红色区域表示。]]

In probability theory, particularly information theory, the conditional mutual information is, in its most basic form, the expected value of the mutual information of two random variables given the value of a third.

In probability theory, particularly information theory, the conditional mutual information is, in its most basic form, the expected value of the mutual information of two random variables given the value of a third.

在概率论理论中，特别是信息论中，条件互信息在其最基本的形式中是给定第三个值的两个随机变量的互信息的期望值。

Definition

定义

For random variables [math]\displaystyle{ X }[/math], [math]\displaystyle{ Y }[/math], and [math]\displaystyle{ Z }[/math] with support sets [math]\displaystyle{ \mathcal{X} }[/math], [math]\displaystyle{ \mathcal{Y} }[/math] and [math]\displaystyle{ \mathcal{Z} }[/math], we define the conditional mutual information as

For random variables [math]\displaystyle{ X }[/math], [math]\displaystyle{ Y }[/math], and [math]\displaystyle{ Z }[/math] with support sets [math]\displaystyle{ \mathcal{X} }[/math], [math]\displaystyle{ \mathcal{Y} }[/math] and [math]\displaystyle{ \mathcal{Z} }[/math], we define the conditional mutual information as

对于随机变量 math x / math、 math y / math 和 math z / math，我们将条件互信息定义为

{{Equation box 1

{{Equation box 1

{方程式方框1

|indent =

|indent =

不会有事的

|title=

|title=

标题

|equation =

|equation =

方程式

[math]\displaystyle{ \lt math\gt 数学 I(X;Y|Z) = \int_\mathcal{Z} D_{\mathrm{KL}}( P_{(X,Y)|Z} \| P_{X|Z} \otimes P_{Y|Z} ) dP_{Z} I(X;Y|Z) = \int_\mathcal{Z} D_{\mathrm{KL}}( P_{(X,Y)|Z} \| P_{X|Z} \otimes P_{Y|Z} ) dP_{Z} I (x; y | z) int mathcal { z }(p {(x，y) | z } | p { x | z } otimes p { y | z }) dP { z } }[/math]

</math>

数学

|cellpadding= 2

|cellpadding= 2

2号手术室

|border

|border

边界

|border colour = #0073CF

|border colour = #0073CF

0073CF

|background colour=#F5FFFA}}

|background colour=#F5FFFA}}

5 / fffa }

This may be written in terms of the expectation operator: [math]\displaystyle{ I(X;Y|Z) = \mathbb{E}_Z [D_{\mathrm{KL}}( P_{(X,Y)|Z} \| P_{X|Z} \otimes P_{Y|Z} )] }[/math].

This may be written in terms of the expectation operator: [math]\displaystyle{ I(X;Y|Z) = \mathbb{E}_Z [D_{\mathrm{KL}}( P_{(X,Y)|Z} \| P_{X|Z} \otimes P_{Y|Z} )] }[/math].

这可以用期望运算符来写: math i (x; y | z) mathbb { e } z [ d { mathrm { KL }(p {(x，y) | z } | p { x | z } otimes p { y | z })] / math。

Thus [math]\displaystyle{ I(X;Y|Z) }[/math] is the expected (with respect to [math]\displaystyle{ Z }[/math]) Kullback–Leibler divergence from the conditional joint distribution [math]\displaystyle{ P_{(X,Y)|Z} }[/math] to the product of the conditional marginals [math]\displaystyle{ P_{X|Z} }[/math] and [math]\displaystyle{ P_{Y|Z} }[/math]. Compare with the definition of mutual information.

Thus [math]\displaystyle{ I(X;Y|Z) }[/math] is the expected (with respect to [math]\displaystyle{ Z }[/math]) Kullback–Leibler divergence from the conditional joint distribution [math]\displaystyle{ P_{(X,Y)|Z} }[/math] to the product of the conditional marginals [math]\displaystyle{ P_{X|Z} }[/math] and [math]\displaystyle{ P_{Y|Z} }[/math]. Compare with the definition of mutual information.

因此，数学 i (x; y | z) / math 是从条件联合分布数学 p {(x，y) | z } / math 到条件边际数学 p { x | z } / math 和数学 p { y | z } / math 的乘积的 Kullback-Leibler 散度。比较互信息的定义。

In terms of pmf's for discrete distributions

根据离散分布的 pmf

For discrete random variables [math]\displaystyle{ X }[/math], [math]\displaystyle{ Y }[/math], and [math]\displaystyle{ Z }[/math] with support sets [math]\displaystyle{ \mathcal{X} }[/math], [math]\displaystyle{ \mathcal{Y} }[/math] and [math]\displaystyle{ \mathcal{Z} }[/math], the conditional mutual information [math]\displaystyle{ I(X;Y|Z) }[/math] is as follows

For discrete random variables [math]\displaystyle{ X }[/math], [math]\displaystyle{ Y }[/math], and [math]\displaystyle{ Z }[/math] with support sets [math]\displaystyle{ \mathcal{X} }[/math], [math]\displaystyle{ \mathcal{Y} }[/math] and [math]\displaystyle{ \mathcal{Z} }[/math], the conditional mutual information [math]\displaystyle{ I(X;Y|Z) }[/math] is as follows

对于离散随机变量 math x / math、 math y / math 和 math z / math，带有支持集 math mathcal { x } / math、 math mathcal { y } / math 和 math mathcal { z } / math，条件互信息 math i (x; y | z) / math 如下

[math]\displaystyle{ \lt math\gt 数学 I(X;Y|Z) = \sum_{z\in \mathcal{Z}} p_Z(z) \sum_{y\in \mathcal{Y}} \sum_{x\in \mathcal{X}} I(X;Y|Z) = \sum_{z\in \mathcal{Z}} p_Z(z) \sum_{y\in \mathcal{Y}} \sum_{x\in \mathcal{X}} I (x; y | z) sum { z } p (z) sum { y }{ y }{ x }{ x }{ x }{ x }}} p_{X,Y|Z}(x,y|z) \log \frac{p_{X,Y|Z}(x,y|z)}{p_{X|Z}(x|z)p_{Y|Z}(y|z)} p_{X,Y|Z}(x,y|z) \log \frac{p_{X,Y|Z}(x,y|z)}{p_{X|Z}(x|z)p_{Y|Z}(y|z)} P { x，y | z }(x，y | z) log frac { x，y | z }(x，y | z)}{ p { x | z }(x | z) p { y | z }(y | z)}(y | z)} }[/math]

</math>

数学

where the marginal, joint, and/or conditional probability mass functions are denoted by [math]\displaystyle{ p }[/math] with the appropriate subscript. This can be simplified as

where the marginal, joint, and/or conditional probability mass functions are denoted by [math]\displaystyle{ p }[/math] with the appropriate subscript. This can be simplified as

其中边际函数、连接函数和 / 或条件概率质量函数用数学 p / math 表示，并附有适当的下标。这可以简化为

{{Equation box 1

{{Equation box 1

{方程式方框1

|indent =

|indent =

不会有事的

|title=

|title=

标题

|equation =

|equation =

方程式

[math]\displaystyle{ \lt math\gt 数学 I(X;Y|Z) = \sum_{z\in \mathcal{Z}} \sum_{y\in \mathcal{Y}} \sum_{x\in \mathcal{X}} p_{X,Y,Z}(x,y,z) \log \frac{p_Z(z)p_{X,Y,Z}(x,y,z)}{p_{X,Z}(x,z)p_{Y,Z}(y,z)}. I(X;Y|Z) = \sum_{z\in \mathcal{Z}} \sum_{y\in \mathcal{Y}} \sum_{x\in \mathcal{X}} p_{X,Y,Z}(x,y,z) \log \frac{p_Z(z)p_{X,Y,Z}(x,y,z)}{p_{X,Z}(x,z)p_{Y,Z}(y,z)}. I (x; y | z) sum { z }{ y }{ x，y，z }(x，y，z) log frac (z) p { x，y，z }(x，y，z)}(x，y，z)}{ x，z }(z)}(x，z){ z，z }(x，z) p { y，z }(y，z)}(y，z)}. }[/math]

</math>

数学

|cellpadding= 6

|cellpadding= 6

6号手术室

|border

|border

边界

|border colour = #0073CF

|border colour = #0073CF

0073CF

|background colour=#F5FFFA}}

|background colour=#F5FFFA}}

5 / fffa }

In terms of pdf's for continuous distributions

对于连续分布，使用 pdf 表示

For (absolutely) continuous random variables [math]\displaystyle{ X }[/math], [math]\displaystyle{ Y }[/math], and [math]\displaystyle{ Z }[/math] with support sets [math]\displaystyle{ \mathcal{X} }[/math], [math]\displaystyle{ \mathcal{Y} }[/math] and [math]\displaystyle{ \mathcal{Z} }[/math], the conditional mutual information [math]\displaystyle{ I(X;Y|Z) }[/math] is as follows

For (absolutely) continuous random variables [math]\displaystyle{ X }[/math], [math]\displaystyle{ Y }[/math], and [math]\displaystyle{ Z }[/math] with support sets [math]\displaystyle{ \mathcal{X} }[/math], [math]\displaystyle{ \mathcal{Y} }[/math] and [math]\displaystyle{ \mathcal{Z} }[/math], the conditional mutual information [math]\displaystyle{ I(X;Y|Z) }[/math] is as follows

对于(绝对)连续随机变量 math x / math、 math y / math 和 math z / math，带有支持集 math mathcal { x } / math、 math mathcal { y } / math 和 math mathcal { z } / math，条件互信息 math i (x; y | z) / math 如下

[math]\displaystyle{ \lt math\gt 数学 I(X;Y|Z) = \int_{\mathcal{Z}} \bigg( \int_{\mathcal{Y}} \int_{\mathcal{X}} I(X;Y|Z) = \int_{\mathcal{Z}} \bigg( \int_{\mathcal{Y}} \int_{\mathcal{X}} I (x; y | z) int { mathcal { z } bigg ( int { mathcal { y } int { mathcal { x } \log \left(\frac{p_{X,Y|Z}(x,y|z)}{p_{X|Z}(x|z)p_{Y|Z}(y|z)}\right) p_{X,Y|Z}(x,y|z) dx dy \bigg) p_Z(z) dz \log \left(\frac{p_{X,Y|Z}(x,y|z)}{p_{X|Z}(x|z)p_{Y|Z}(y|z)}\right) p_{X,Y|Z}(x,y|z) dx dy \bigg) p_Z(z) dz (x，y | z)}{ x | z }(x | z) p { y | z }(y | z)}(右) p { x，y | z }(x，y | z) dx dy bigg) p z (z) dz }[/math]

</math>

数学

where the marginal, joint, and/or conditional probability density functions are denoted by [math]\displaystyle{ p }[/math] with the appropriate subscript. This can be simplified as

where the marginal, joint, and/or conditional probability density functions are denoted by [math]\displaystyle{ p }[/math] with the appropriate subscript. This can be simplified as

其中边际，联合和 / 或条件概率密度函数用数学 p / math 表示，并附有适当的下标。这可以简化为

{{Equation box 1

{{Equation box 1

{方程式方框1

|indent =

|indent =

不会有事的

|title=

|title=

标题

|equation =

|equation =

方程式

[math]\displaystyle{ \lt math\gt 数学 I(X;Y|Z) = \int_{\mathcal{Z}} \int_{\mathcal{Y}} \int_{\mathcal{X}} \log \left(\frac{p_Z(z)p_{X,Y,Z}(x,y,z)}{p_{X,Z}(x,z)p_{Y,Z}(y,z)}\right) p_{X,Y,Z}(x,y,z) dx dy dz. I(X;Y|Z) = \int_{\mathcal{Z}} \int_{\mathcal{Y}} \int_{\mathcal{X}} \log \left(\frac{p_Z(z)p_{X,Y,Z}(x,y,z)}{p_{X,Z}(x,z)p_{Y,Z}(y,z)}\right) p_{X,Y,Z}(x,y,z) dx dy dz. I (x; y | z) int mathcal { y } int mathcal { x } log left (frac z (z) p { x，y，z }(x，y，z)}{ p { x，z }(x，z) p { y，z }(y，z)}{右) p { x，y，z }(z)}(x，y，z)}(dy) dz。 }[/math]

</math>

数学

|cellpadding= 6

|cellpadding= 6

6号手术室

|border

|border

边界

|border colour = #0073CF

|border colour = #0073CF

0073CF

|background colour=#F5FFFA}}

|background colour=#F5FFFA}}

5 / fffa }

Some identities

一些身份

Alternatively, we may write in terms of joint and conditional entropies as

Alternatively, we may write in terms of joint and conditional entropies as

或者，我们可以写联合和条件熵作为

[math]\displaystyle{ I(X;Y|Z) = H(X,Z) + H(Y,Z) - H(X,Y,Z) - H(Z) \lt math\gt I(X;Y|Z) = H(X,Z) + H(Y,Z) - H(X,Y,Z) - H(Z) 数学 i (x; y | z) h (x，z) + h (y，z)-h (x，y，z)-h (z) = H(X|Z) - H(X|Y,Z) = H(X|Z)+H(Y|Z)-H(X,Y|Z). }[/math]

               = H(X|Z) - H(X|Y,Z) = H(X|Z)+H(Y|Z)-H(X,Y|Z).</math>

H (x | z)-h (x | y，z) h (x | z) + h (y | z)-h (x，y | z) . / math

This can be rewritten to show its relationship to mutual information

This can be rewritten to show its relationship to mutual information

这可以重写以显示它与互信息的关系

[math]\displaystyle{ I(X;Y|Z) = I(X;Y,Z) - I(X;Z) }[/math]

[math]\displaystyle{ I(X;Y|Z) = I(X;Y,Z) - I(X;Z) }[/math]

数学 i (x; y | z) i (x; y，z)-i (x; z) / math

usually rearranged as the chain rule for mutual information

usually rearranged as the chain rule for mutual information

通常重新排列，作为互信息的链式规则

[math]\displaystyle{ I(X;Y,Z) = I(X;Z) + I(X;Y|Z) }[/math]

[math]\displaystyle{ I(X;Y,Z) = I(X;Z) + I(X;Y|Z) }[/math]

数学 i (x; y，z) i (x; z) + i (x; y | z) / math

Another equivalent form of the above is

Another equivalent form of the above is

另一个类似的形式是

[math]\displaystyle{ I(X;Y|Z) = H(Z|X) + H(X) + H(Z|Y) + H(Y) - H(Z|X,Y) - H(X,Y) - H(Z) \lt math\gt I(X;Y|Z) = H(Z|X) + H(X) + H(Z|Y) + H(Y) - H(Z|X,Y) - H(X,Y) - H(Z) H (z | x) + h (x) + h (z | y) + h (y)-h (z | x，y)-h (x，y)-h (z) = I(X;Y) + H(Z|X) + H(Z|Y) - H(Z|X,Y) - H(Z) }[/math]

               = I(X;Y) + H(Z|X) + H(Z|Y) - H(Z|X,Y) - H(Z)</math>

I (x; y) + h (z | x) + h (z | y)-h (z | x，y)-h (z) / math

Like mutual information, conditional mutual information can be expressed as a Kullback–Leibler divergence:

Like mutual information, conditional mutual information can be expressed as a Kullback–Leibler divergence:

与互信息一样，条件互信息也可以表示为 Kullback-Leibler 背离:

[math]\displaystyle{ I(X;Y|Z) = D_{\mathrm{KL}}[ p(X,Y,Z) \| p(X|Z)p(Y|Z)p(Z) ]. }[/math]

[math]\displaystyle{ I(X;Y|Z) = D_{\mathrm{KL}}[ p(X,Y,Z) \| p(X|Z)p(Y|Z)p(Z) ]. }[/math]

数学 i (x; y | z) d { mathrm { KL }[ p (x，y，z) | p (x | z) p (y | z) p (z)]。数学

Or as an expected value of simpler Kullback–Leibler divergences:

Or as an expected value of simpler Kullback–Leibler divergences:

或者作为一个更简单的 Kullback-Leibler 分歧的期望值:

[math]\displaystyle{ I(X;Y|Z) = \sum_{z \in \mathcal{Z}} p( Z=z ) D_{\mathrm{KL}}[ p(X,Y|z) \| p(X|z)p(Y|z) ] }[/math],

[math]\displaystyle{ I(X;Y|Z) = \sum_{z \in \mathcal{Z}} p( Z=z ) D_{\mathrm{KL}}[ p(X,Y|z) \| p(X|z)p(Y|z) ] }[/math],

数学 i (x; y | z) sum { z } p (z) d { mathrum { KL }[ p (x，y | z) | p (x | z) p (y | z)] / math,

[math]\displaystyle{ I(X;Y|Z) = \sum_{y \in \mathcal{Y}} p( Y=y ) D_{\mathrm{KL}}[ p(X,Z|y) \| p(X|Z)p(Z|y) ] }[/math].

[math]\displaystyle{ I(X;Y|Z) = \sum_{y \in \mathcal{Y}} p( Y=y ) D_{\mathrm{KL}}[ p(X,Z|y) \| p(X|Z)p(Z|y) ] }[/math].

数学 i (x; y | z) sum { y } p (y) d { mathrum { KL }[ p (x，z | y) | p (x | z) p (z | y)] / math。

More general definition

更一般的定义

A more general definition of conditional mutual information, applicable to random variables with continuous or other arbitrary distributions, will depend on the concept of regular conditional probability. (See also.)

A more general definition of conditional mutual information, applicable to random variables with continuous or other arbitrary distributions, will depend on the concept of regular conditional probability. (See also.)

条件互信息的更一般的定义---- 适用于具有连续或其他任意分布的随机变量---- 取决于正则条件概率的概念。(另见。)

Let [math]\displaystyle{ (\Omega, \mathcal F, \mathfrak P) }[/math] be a probability space, and let the random variables [math]\displaystyle{ X }[/math], [math]\displaystyle{ Y }[/math], and [math]\displaystyle{ Z }[/math] each be defined as a Borel-measurable function from [math]\displaystyle{ \Omega }[/math] to some state space endowed with a topological structure.

Let [math]\displaystyle{ (\Omega, \mathcal F, \mathfrak P) }[/math] be a probability space, and let the random variables [math]\displaystyle{ X }[/math], [math]\displaystyle{ Y }[/math], and [math]\displaystyle{ Z }[/math] each be defined as a Borel-measurable function from [math]\displaystyle{ \Omega }[/math] to some state space endowed with a topological structure.

让 math ( Omega， mathcal f， mathfrak p) / math 是一个概率空间，让随机变量 math x / math，math y / math，math z / math 都被定义为 borel-measured 函数，从 math Omega / math 到某个具有拓扑结构的状态空间。

Consider the Borel measure (on the σ-algebra generated by the open sets) in the state space of each random variable defined by assigning each Borel set the [math]\displaystyle{ \mathfrak P }[/math]-measure of its preimage in [math]\displaystyle{ \mathcal F }[/math]. This is called the pushforward measure [math]\displaystyle{ X _* \mathfrak P = \mathfrak P\big(X^{-1}(\cdot)\big). }[/math] The support of a random variable is defined to be the topological support of this measure, i.e. [math]\displaystyle{ \mathrm{supp}\,X = \mathrm{supp}\,X _* \mathfrak P. }[/math]

Consider the Borel measure (on the σ-algebra generated by the open sets) in the state space of each random variable defined by assigning each Borel set the [math]\displaystyle{ \mathfrak P }[/math]-measure of its preimage in [math]\displaystyle{ \mathcal F }[/math]. This is called the pushforward measure [math]\displaystyle{ X _* \mathfrak P = \mathfrak P\big(X^{-1}(\cdot)\big). }[/math] The support of a random variable is defined to be the topological support of this measure, i.e. [math]\displaystyle{ \mathrm{supp}\,X = \mathrm{supp}\,X _* \mathfrak P. }[/math]

考虑一个 Borel 测度(在开集生成的-代数上)在每个随机变量的状态空间中，通过赋予每个 Borel 集在数学数学 f / math 中它的前映象的数学问题 p / 数学测度来定义。这被称为前推测度数学 x * mathfrak p mathfrak p big (x ^ {-1}(cdot) big)。 随机变量的支持被定义为这个度量的拓扑支持，例如。数学问题，数学问题，数学问题，数学问题

Now we can formally define the conditional probability measure given the value of one (or, via the product topology, more) of the random variables. Let [math]\displaystyle{ M }[/math] be a measurable subset of [math]\displaystyle{ \Omega, }[/math] (i.e. [math]\displaystyle{ M \in \mathcal F, }[/math]) and let [math]\displaystyle{ x \in \mathrm{supp}\,X. }[/math] Then, using the disintegration theorem:

Now we can formally define the conditional probability measure given the value of one (or, via the product topology, more) of the random variables. Let [math]\displaystyle{ M }[/math] be a measurable subset of [math]\displaystyle{ \Omega, }[/math] (i.e. [math]\displaystyle{ M \in \mathcal F, }[/math]) and let [math]\displaystyle{ x \in \mathrm{supp}\,X. }[/math] Then, using the disintegration theorem:

现在，我们可以正式定义给定一个(或者，通过条件概率积空间，更多)的随机变量的值。设 m / math 是 math Omega 的一个可测子集，即。然后，利用瓦解定理:

[math]\displaystyle{ \mathfrak P(M | X=x) = \lim_{U \ni x} \lt math\gt \mathfrak P(M | X=x) = \lim_{U \ni x} Math mathfrak p (m | x) lim { u ni } \frac {\mathfrak P(M \cap \{X \in U\})} \frac {\mathfrak P(M \cap \{X \in U\})} 数学问题(医学问题)(英文) {\mathfrak P(\{X \in U\})} {\mathfrak P(\{X \in U\})} { mathfrak p ( xin u } \qquad \textrm{and} \qquad \mathfrak P(M|X) = \int_M d\mathfrak P\big(\omega|X=X(\omega)\big), }[/math]

 \qquad \textrm{and} \qquad \mathfrak P(M|X) = \int_M d\mathfrak P\big(\omega|X=X(\omega)\big),</math>

(m | x) int md mathfrak p big ( omega | x ( omega) big) ，/ math

where the limit is taken over the open neighborhoods [math]\displaystyle{ U }[/math] of [math]\displaystyle{ x }[/math], as they are allowed to become arbitrarily smaller with respect to set inclusion.

where the limit is taken over the open neighborhoods [math]\displaystyle{ U }[/math] of [math]\displaystyle{ x }[/math], as they are allowed to become arbitrarily smaller with respect to set inclusion.

这里的极限取代了开放社区的数学 u / math of math x / math，因为它们被允许随着包含性的设置而任意缩小。

Finally we can define the conditional mutual information via Lebesgue integration:

Finally we can define the conditional mutual information via Lebesgue integration:

最后，我们可以通过勒贝格积分来定义条件互信息:

[math]\displaystyle{ I(X;Y|Z) = \int_\Omega \log \lt math\gt I(X;Y|Z) = \int_\Omega \log Math i (x; y | z) int Omega log \Bigl( \Bigl( Bigl ( \frac {d \mathfrak P(\omega|X,Z)\, d\mathfrak P(\omega|Y,Z)} \frac {d \mathfrak P(\omega|X,Z)\, d\mathfrak P(\omega|Y,Z)} { omega | x，z } ，d mathfrak p ( omega | y，z)} {d \mathfrak P(\omega|Z)\, d\mathfrak P(\omega|X,Y,Z)} {d \mathfrak P(\omega|Z)\, d\mathfrak P(\omega|X,Y,Z)} { d mathfrak p ( omega | z) ，d mathfrak p ( omega | x，y，z)} \Bigr) \Bigr) Bigr) d \mathfrak P(\omega), d \mathfrak P(\omega), D mathfrak p ( omega) , }[/math]

 </math>

数学

where the integrand is the logarithm of a Radon–Nikodym derivative involving some of the conditional probability measures we have just defined.

where the integrand is the logarithm of a Radon–Nikodym derivative involving some of the conditional probability measures we have just defined.

其中被积函数是 Radon-Nikodym 导数的对数，它包含了我们刚才定义的条件概率测度。

Note on notation

关于符号的注释

In an expression such as [math]\displaystyle{ I(A;B|C), }[/math] [math]\displaystyle{ A, }[/math] [math]\displaystyle{ B, }[/math] and [math]\displaystyle{ C }[/math] need not necessarily be restricted to representing individual random variables, but could also represent the joint distribution of any collection of random variables defined on the same probability space. As is common in probability theory, we may use the comma to denote such a joint distribution, e.g. [math]\displaystyle{ I(A_0,A_1;B_1,B_2,B_3|C_0,C_1). }[/math] Hence the use of the semicolon (or occasionally a colon or even a wedge [math]\displaystyle{ \wedge }[/math]) to separate the principal arguments of the mutual information symbol. (No such distinction is necessary in the symbol for joint entropy, since the joint entropy of any number of random variables is the same as the entropy of their joint distribution.)

In an expression such as [math]\displaystyle{ I(A;B|C), }[/math] [math]\displaystyle{ A, }[/math] [math]\displaystyle{ B, }[/math] and [math]\displaystyle{ C }[/math] need not necessarily be restricted to representing individual random variables, but could also represent the joint distribution of any collection of random variables defined on the same probability space. As is common in probability theory, we may use the comma to denote such a joint distribution, e.g. [math]\displaystyle{ I(A_0,A_1;B_1,B_2,B_3|C_0,C_1). }[/math] Hence the use of the semicolon (or occasionally a colon or even a wedge [math]\displaystyle{ \wedge }[/math]) to separate the principal arguments of the mutual information symbol. (No such distinction is necessary in the symbol for joint entropy, since the joint entropy of any number of random variables is the same as the entropy of their joint distribution.)

在一个表达式中，如 math i (a; b | c) ，/ math math math a，/ math b，/ math 和 math c / math 不一定要局限于表示单个的随机变量，但也可以表示在同一个概率空间上定义的任何随机变量集合的联合分布。正如在概率论中常见的那样，我们可以用逗号来表示这种联合分布，例如:。数学 i (a0，a1; b1，b2，b3 | c0，c1)。 因此，使用分号(或偶尔冒号，甚至楔形数学楔形数学 / math)来分隔互信息符号的主要参数。(在联合熵的符号中不需要这样的区分，因为任意数目的随机变量的联合熵等于它们联合分布的联合熵。)

Properties

属性

Nonnegativity

非消极性

It is always true that

It is always true that

事实总是如此

[math]\displaystyle{ I(X;Y|Z) \ge 0 }[/math],

[math]\displaystyle{ I(X;Y|Z) \ge 0 }[/math],

数学 i (x; y | z) ge 0 / math,

for discrete, jointly distributed random variables [math]\displaystyle{ X }[/math], [math]\displaystyle{ Y }[/math] and [math]\displaystyle{ Z }[/math]. This result has been used as a basic building block for proving other inequalities in information theory, in particular, those known as Shannon-type inequalities.

for discrete, jointly distributed random variables [math]\displaystyle{ X }[/math], [math]\displaystyle{ Y }[/math] and [math]\displaystyle{ Z }[/math]. This result has been used as a basic building block for proving other inequalities in information theory, in particular, those known as Shannon-type inequalities.

对于离散的，联合分布的随机变量，数学 x / math，数学 y / math 和数学 z / math。这个结果被用来作为证明信息论中其他不等式的基本构件，特别是那些被称为香农型不等式的不等式。

Interaction information

互动信息

Conditioning on a third random variable may either increase or decrease the mutual information: that is, the difference [math]\displaystyle{ I(X;Y) - I(X;Y|Z) }[/math], called the interaction information, may be positive, negative, or zero. This is the case even when random variables are pairwise independent. Such is the case when: [math]\displaystyle{ X \sim \mathrm{Bernoulli}(0.5), Z \sim \mathrm{Bernoulli}(0.5), \quad Y=\left\{\begin{array}{ll} X & \text{if }Z=0\\ 1-X & \text{if }Z=1 \end{array}\right. }[/math]in which case [math]\displaystyle{ X }[/math], [math]\displaystyle{ Y }[/math] and [math]\displaystyle{ Z }[/math] are pairwise independent and in particular [math]\displaystyle{ I(X;Y)=0 }[/math], but [math]\displaystyle{ I(X;Y|Z)=1. }[/math]

Conditioning on a third random variable may either increase or decrease the mutual information: that is, the difference [math]\displaystyle{ I(X;Y) - I(X;Y|Z) }[/math], called the interaction information, may be positive, negative, or zero. This is the case even when random variables are pairwise independent. Such is the case when: [math]\displaystyle{ X \sim \mathrm{Bernoulli}(0.5), Z \sim \mathrm{Bernoulli}(0.5), \quad Y=\left\{\begin{array}{ll} X & \text{if }Z=0\\ 1-X & \text{if }Z=1 \end{array}\right. }[/math]in which case [math]\displaystyle{ X }[/math], [math]\displaystyle{ Y }[/math] and [math]\displaystyle{ Z }[/math] are pairwise independent and in particular [math]\displaystyle{ I(X;Y)=0 }[/math], but [math]\displaystyle{ I(X;Y|Z)=1. }[/math]

对第三个随机变量的条件作用可以增加或减少互信息: 也就是说，差分数学 i (x; y)-i (x; y | z) / 数学，称为交互信息，可以是正的、负的或零的。即使随机变量是成对独立的，情况也是如此。例如: math display"block"x | sim | mathrum { Bernoulli }(0.5) ，z | sim | mathrum { Bernoulli }(0.5) ，y | left | begin | array | text | if | z0 | 1 | end | array | right。 在这种情况下，数学 x / 数学，数学 y / 数学和数学 z / 数学是成对独立的，特别是数学 i (x; y)0 / 数学，但数学 i (x; y | z)1。 数学

Chain rule for mutual information

互信息链规则

[math]\displaystyle{ I(X;Y,Z) = I(X;Z) + I(X;Y|Z) }[/math]

[math]\displaystyle{ I(X;Y,Z) = I(X;Z) + I(X;Y|Z) }[/math]

数学 i (x; y，z) i (x; z) + i (x; y | z) / math

Multivariate mutual information

多元互信息

Main article: Multivariate mutual information

The conditional mutual information can be used to inductively define a multivariate mutual information in a set- or measure-theoretic sense in the context of information diagrams. In this sense we define the multivariate mutual information as follows:

The conditional mutual information can be used to inductively define a multivariate mutual information in a set- or measure-theoretic sense in the context of information diagrams. In this sense we define the multivariate mutual information as follows:

在信息图的背景下，条件互信息可以用集合或测度理论的意义归纳地定义多元互信息。在这个意义上，我们将多元互信息定义如下:

[math]\displaystyle{ I(X_1;\ldots;X_{n+1}) = I(X_1;\ldots;X_n) - I(X_1;\ldots;X_n|X_{n+1}), }[/math]

[math]\displaystyle{ I(X_1;\ldots;X_{n+1}) = I(X_1;\ldots;X_n) - I(X_1;\ldots;X_n|X_{n+1}), }[/math]

Math i (x1; ldots; x{ n + 1}) i (x1; ldots; xn)-i (x1; ldots; xn | x { n + 1}) ，/ math

where

where

在哪里

[math]\displaystyle{ I(X_1;\ldots;X_n|X_{n+1}) = \mathbb{E}_{X_{n+1}} [D_{\mathrm{KL}}( P_{(X_1,\ldots,X_n)|X_{n+1}} \| P_{X_1|X_{n+1}} \otimes\cdots\otimes P_{X_n|X_{n+1}} )]. }[/math]

[math]\displaystyle{ I(X_1;\ldots;X_n|X_{n+1}) = \mathbb{E}_{X_{n+1}} [D_{\mathrm{KL}}( P_{(X_1,\ldots,X_n)|X_{n+1}} \| P_{X_1|X_{n+1}} \otimes\cdots\otimes P_{X_n|X_{n+1}} )]. }[/math]

数学 i (x1; ldots; xn | x { n + 1}) mathbb { x { n + 1}[ d { x {(x1，ldots，xn) | x { n + 1} | p { x1 | x { n + 1}} o 乘以 p { x n | x { n + 1}]]

This definition is identical to that of interaction information except for a change in sign in the case of an odd number of random variables. A complication is that this multivariate mutual information (as well as the interaction information) can be positive, negative, or zero, which makes this quantity difficult to interpret intuitively. In fact, for [math]\displaystyle{ n }[/math] random variables, there are [math]\displaystyle{ 2^n-1 }[/math] degrees of freedom for how they might be correlated in an information-theoretic sense, corresponding to each non-empty subset of these variables. These degrees of freedom are bounded by various Shannon- and non-Shannon-type inequalities in information theory.

This definition is identical to that of interaction information except for a change in sign in the case of an odd number of random variables. A complication is that this multivariate mutual information (as well as the interaction information) can be positive, negative, or zero, which makes this quantity difficult to interpret intuitively. In fact, for [math]\displaystyle{ n }[/math] random variables, there are [math]\displaystyle{ 2^n-1 }[/math] degrees of freedom for how they might be correlated in an information-theoretic sense, corresponding to each non-empty subset of these variables. These degrees of freedom are bounded by various Shannon- and non-Shannon-type inequalities in information theory.

这个定义与交互信息的定义相同，只是在随机变量为奇数的情况下，符号发生了变化。一个复杂的问题是，这个多元互信息(以及交互信息)可以是正的、负的或零的，这使得这个量很难直观地解释。事实上，对于数学 n / math 随机变量，对于它们在信息理论意义上如何相关，存在2 ^ n-1 / math 自由度，对应于这些变量的每个非空子集。这些自由度受到信息论中各种香农型和非香农型不等式的限制。

References

参考资料

Category:Information theory

范畴: 信息论

Category:Entropy and information

类别: 熵和信息

This page was moved from wikipedia:en:Conditional mutual information. Its edit history can be viewed at 条件互信息/edithistory